Pochodne wyższe i szereg Taylora
Pochodne wyższych rzędów — definicja i przykłady
Pochodne wyższych rzędów
Drugą pochodną funkcji [math]f\;[/math] nazywamy pochodną pochodnej tej funkcji. Trzecia pochodna jest pochodną drugiej pochodnej; itd. Ogólnie, [math]n\;[/math] -ta pochodna funkcji jest pochodną [math]n-1\;[/math] —wszej pochodnej.
Oznaczenia
Pochodne wyższych rzędów oznaczamy
Mamy więc
Uwaga
Dogodnie jest przy tym zdefiniować pochodną rzędu zerowego jako samą funkcję:
Przykłady
- Dla [math]f(x)=x^3\;[/math] mamy: [math]f'(x)=3x^2\;[/math], [math]f''(x)=6x\;[/math], [math]f'''(x)=6\;[/math], a wszystkie wyższe pochodne są równe zeru.
- Ogólnie: [math]k-\;[/math] ta pochodna funkcji [math]f(x)=x^n\;[/math] jest
[math] f^{(k)}(x)=n(n-1)\dots(n-k+1) x^{n-k} \;\;\;{\rm dla}\;\;k\lt n\;\;\;f^{(n)}(x)=n!, [/math]a wyższe pochodne są równe zeru.
- [math]k-\;[/math] ta pochodna funkcji [math]f(x)=x^a\;[/math], gdzie [math]a\in \mathbb R \; \;[/math] oraz [math]x\gt 0\;[/math], jest równa
[math] f^{(k)}(x)=a(a-1)\dots(a-k+1) x^{a-k}; [/math]
- [math](e^x)'=e^x\;[/math], co daje, że wszystkie wyższe pochodne funkcji [math]e^x\;[/math] są równe [math]e^x\;[/math].
- Dla funkcji [math]f(x)=\sin\; x\;[/math] mamy
[math] f'(x)=\cos\; x;\;\;\; f''(x)=-\sin\; x;\;\;\; f'''(x)=-\cos\; x; \;\;\; f^{(4)}(x)=\sin\; x; [/math]
to było dla pierwszych czterech pochodnych, a dowolną pochodną można obliczyć wykorzystując
tożsamość zawartą wyżej: [math]f^{(n+4)}(x)=f^{(n)}(x)\;[/math]. - Wzór (1) pozwala policzyć dowolną pochodną dowolnego wielomianu
[math]f(x)=a_0+a_1 x +a_2 x^2 +\dots+a_n x^n\;.[/math] Nie będziemy tego wypisywać in extenso, (wzór ten jest dość skomplikowany i nie mamy tu potrzeby wypisywać go), a weźmy jego szczególny przypadek, tzn. wypiszmy pochodne od 0 do [math]n\;[/math] w punkcie [math]x=0\;[/math]. Mamy[1]:
[math] a_0=f(0), \; a_1=f'(0), \;a_2=\frac{1}{2!}f''(0),\dots, a_n=\frac{1}{n!}f^{(n)}(0). ;[/math]
Stąd wynika wzór:
[math] f(x)=f(0)+x f'(0) + \frac{x^2}{2!} f''(0) + \dots + \frac{x^k}{k!} f^{(k)}(0) + \dots+ \frac{x^n}{n!} f^{(n)}(0). [/math]
[math]n\;[/math]-ta pochodna iloczynu funkcji — wzór Leibniza
Na [math]n-\;[/math] tą pochodną sumy i różnicy sumy dwóch funkcji mamy proste wzory
(natychmiastowy dowód indukcyjny: W pierwszym kroku: [math](f(x)+g(x))' = f'(x) \pm g'(x)\;[/math] ; dalej: [math](f(x)+g(x))^{(n)} = ((f(x)+g(x))^{(n-1)})' = (f^{(n-1)}(x) \pm g^{(n-1)}(x))'=f^{(n)}(x) \pm g^{(n)}(x)\;[/math] ; i na mocy zasady indukcji wzór (3) jest prawdziwy dla każdego [math]n\;[/math].)
Dla [math]n-\;[/math] tej pochodnej iloczynu funkcji wzór jest bardziej skomplikowany, ale dający się ogarnąć:
Twierdzenie (wzór Leibnitza)
[math]n-\;[/math] ta pochodna iloczynu dwóch funkcji dana jest wzorem
(dla prostoty nie pisaliśmy jawnej zależności od [math]x\;[/math] ; wszędzie wyżej należy pamiętać, że [math]f\equiv f(x)\;[/math], [math]f^{(k)}\equiv f^{(k)}(x)\;[/math] itd.)
Dowód
będzie indukcyjny. Dla [math]n=1\;[/math] otrzymujemy znany już wzór na pochodną iloczynu. Załóżmy, że wzór (4) zachodzi dla [math]n\;[/math] i obliczmy pochodną obu jego stron. Z twierdzenia o pochodnej iloczynu mamy
ostatnia równość wynika z faktu, iż mamy dla współczynników Newtona
(wzór ten był pokazywany przy dowodzie wzoru dwumiennego Newtona).
CBDO
Przykład
Obliczmy drugą pochodną funkcji odwrotnej. Najsampierw wyprowadźmy raz jeszcze wzór na tę pochodną, korzystając z wzoru na pochodną funkcji złożonej. Jeśli [math]f(x)\;[/math] — funkcja, a [math]f^{-1}(x)\;[/math] — funkcja do niej odwrotna, to mamy: [math]f^{-1}(f(x))=x\;[/math], skąd po zróżniczkowaniu otrzymamy
co daje
Obustronnie różniczkując, otrzymujemy
co daje
Różniczkując ten wzór, można uzyskać dowolną wyższą pochodną.
Wzór Taylora
Twierdzenie (Wzór Taylora)
Załóżmy, że funkcja [math]f\;[/math] jest [math]n-\;[/math] krotnie różniczkowalna w przedziale [math][a,b]\;[/math]. Oznaczmy [math]h=b-a\;[/math]. Wtedy zachodzi
gdzie wyraz [math]R_n\;[/math], zwany resztą [math]n-\;[/math] tego rzędu, można przedstawić w jednej z postaci
(reszta w postaci Lagrange'a), lub
(reszta w postaci Cauchy'ego).
Uwaga przed dowodem
Wzór Taylora można uważać za uogólnienie wzoru Lagrange'a: Ten ostatni to szczególny przypadek wzoru Taylora dla [math]n=1\;[/math].
Dowód
Wypiszmy z wzoru (6) resztę:
[math] R_n= f(b)-f(a) - \frac{f'(a)}{1!}(b-a) - \frac{f''(a)}{2!}(b-a)^2- \dots - \frac{f^{(n-1)}(a)}{(n-1)!} (b-a)^{n-1} [/math]
Oznaczmy przez [math]g_n(x)\;[/math] funkcję pomocniczą zdefiniowaną w ten sposób, że w [math]R_n\;[/math] zastępujemy [math]a\;[/math] przez [math]x\;[/math] :
[math] g_n(x)= f(b)-f(x) - \frac{f'(x)}{1!}(b-x) - \frac{f''(x)}{2!}(b-x)^2- \dots - \frac{f^{(n-1)}(x)}{(n-1)!} (b-x)^{n-1} \;[/math]
Pochodna funkcji [math]g_n(x)\;[/math] jest równa:
W powyższej sumie kasują się więc wszystkie człony oprócz ostatniego i mamy
Zarazem: [math]g_n(b)=0\;[/math], [math]g_n(a)=R_n\;[/math]. Stosując do funkcji [math]g_n(x)\;[/math] twierdzenie Lagrange'a o wartości średniej, otrzymujemy
więc
skąd otrzymujemy
czyli resztę w postaci Cauchy'ego (8).
Pozostaje pokazać, że równoważną postacią reszty jest postać Lagrange'a (7). W dowodzie używa się wzoru Cauchy'ego o wartości średniej z funkcjami: [math]g_n(x)\;[/math] i [math]u_n(x)=(b-x)^n\;[/math]. Wzór Cauchy'ego o wartości średniej mówi, że:
Tu mamy: [math]u_n(b)=0\;[/math], [math]u_n(a)=h^n\;[/math], [math]u'_n(x)=-n(b-x)^{n-1}\;[/math], skąd wynika, uwzględniając (9)
czyli otrzymujemy
tzn. postać reszty Lagrange'a (7).
Uwagi
- Wzoru Taylora zazwyczaj używa się w postaci:
[math] f(x+h)=f(x)+\frac{f'(x)}{1!}h + \frac{f''(x)}{2!}h^2+ \dots \frac{f^{(n-1)}(x)}{(n-1)!} h^{n-1}+ R_n [/math]
Można na ten wzór patrzeć jako na przybliżenie funkcji w otoczeniu punktu [math]x\;[/math] przez wielomian ([math]n-\;[/math] tego stopnia). Jeśli umiemy oszacować resztę, to daje nam ona dokładność tego przybliżenia.
Dla [math]x=0\;[/math], powyższa wersja wzoru Taylora nazywana jest wzorem Maclaurina - Gdy funkcja jest różniczkowalna dowolną ilość razy, to reszta może być dowolnie wysokiego rzędu. Okazuje się, że można "odsunąć ją do nieskończoności" — zapisać rozwinięcie Taylora jako nieskończony szereg. Aby to precyzyjnie wyrazić, potrzebne jest pojęcie zbieżności szeregu i jakieś kryteria zbieżności; zajmiemy się tym niedługo.
Przykłady
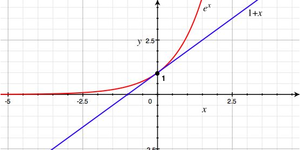
- Zapiszmy wzór Taylora dla funkcji [math]f(x)=e^x\;[/math] w otoczeniu punktu [math]x=0\;[/math] z dokładnością do drugiego rzędu. Mamy: [math]f'(x)=f''(x)=e^x\;[/math], [math]f(0)=f'(0)=f''(0)=1\;[/math], tak więc
[math] e^x=1+x+\frac{x^2}{2} e^{\theta x}, \;\;\;\mbox{gdzie}\;\;\;\theta\in]0,1[. [/math] Stąd wynika, że dla każdego [math]x\;[/math] zachodzi równość
[math] e^x\geq 1+x, \;[/math]
bo reszta jest dodatnia (jako że [math]x^2\gt 0\;[/math] i [math]e^{\theta x}\gt 0\;[/math] ). Nierówność ta posiada wyrazisty sens geometryczny — patrz wykres. - Wzór Taylora pozwala w następujący sposób zwiększyć moc reguły de l'Hospitala:
Twierdzenie
Jeśli funkcje [math]f\;[/math] i [math]g\;[/math] posiadają [math]n-\;[/math] te pochodne ciągłe i jeśli
to
Dowód
We wzorze Taylora (6) [math]b\;[/math] zastąpmy przez [math]x\;[/math]. Z uwagi na znikanie pierwszych [math]n-1\;[/math] pochodnych zostaje tylko sama reszta:
Tak więc
Przechodząc do granicy [math]\displaystyle\mathop{\lim}_{x\to a}\;[/math] i biorąc pod uwagę ciągłość funkcji [math]f^{(n)}\;[/math] i [math]g^{(n)}\;[/math] (podobnie jak to było przy dowodzie zwykłego tw. de l'Hospitala), otrzymujemy wzór (11).
CBDO
Przykład
[math]\displaystyle\mathop{\lim}_{x\to 0} \frac{\sin\; x-x}{x(1-\cos\; x)} = \displaystyle\mathop{\lim}_{x\to 0} \frac{x-\frac{x^3}{3!}+r_4-x}{x-x+\frac{x^3}{2!}+x\tilde{r_3}} = \displaystyle\mathop{\lim}_{x\to 0} \frac{-\frac{1}{3!}+\frac{1}{x^3}r_n}{\frac{1}{2!}+\frac{1}{x^2}\tilde{r_3}} = \frac{-\frac{1}{3!}}{\frac{1}{2!}}=-3\;[/math]
Kryteria na ekstrema
Niedawno pokazaliśmy, że jeśli funkcja (różniczkowalna) [math]f\;[/math] posiada w punkcie [math]x_0\;[/math] ekstremum, to [math]f'(x_0)=0\;[/math]. Pamiętamy też, że na odwrót nie jest: Jeśli [math]f'(x)=0\;[/math], to nie znaczy, że w [math]x_0\;[/math] znajduje się ekstremum (np. dla [math]f(x)=x^3\;[/math] ). Równość [math]f'(x)=0\;[/math] jest więc warunkiem koniecznym, ale niedostatecznym na istnienie tam ekstremum. Okazuje się, że badanie wyższych pochodnych daje ogólniejsze kryterium na istnienie ekstremum:
Twierdzenie
Załóżmy, że funkcja [math]f\;[/math] jest różniczkowalna [math]n-\;[/math] krotnie i [math]n-\;[/math] ta pochodna jest ciągła. Niech również
Wówczas, jeśli [math]n\;[/math] jest parzyste, to w punkcie [math]c\;[/math] funkcja [math]f\;[/math] ma ekstremum właściwe: maksimum, jeśli [math]f^{(n)}\lt 0\;[/math], minimum, jeśli [math]f^{(n)}\gt 0\;[/math]. Jeśli natomiast [math]n\;[/math] jest liczbą nieparzystą, to [math]f\;[/math] nie posiada ekstremum w punkcie [math]c\;[/math].
Dowód
Z wzoru Taylora mamy:
i, ponieważ na mocy założenia pierwszych [math]n-1\;[/math] pochodnych [math]f\;[/math] zeruje się w punkcie [math]c\;[/math], mamy
Załóżmy, że [math]n\;[/math] jest liczbą parzystą. Niech [math]f^{(n)}(c)\lt 0\;[/math]. Ze względu na ciągłość funkcji [math]f^{(n)}(x)\;[/math] w punkcie [math]c\;[/math] istnieje takie [math]\delta\gt 0\;[/math], że nierówność: [math]|x-c|\lt \delta\;[/math] implikuje [math]f^{(n)}(x)\lt 0\;[/math]. Jeśli więc [math]|h|\lt \delta\;[/math], to i [math]\theta h\lt \delta\;[/math], zatem [math]f^{(n)}(c+\theta h)\lt 0\;[/math]. Patrząc teraz na (13) widzimy, że jeśli
(pamiętajmy, że [math]n\;[/math] jest parzyste, więc [math]h^n\gt 0\;[/math] ). Powyższa nierówność oznacza, że w punkcie [math]c\;[/math] funkcja [math]f\;[/math] posiada maksimum. Z analogicznego rozumowania wynika, że jeśli [math]n\;[/math] jest liczbą parzystą i zachodzi: [math]f^{(n)}(c)\gt 0\;[/math], to [math]f(c+h)-f(c)\gt 0\;[/math] (znowu dla [math]h\gt 0\;[/math] i [math]h\lt 0\;[/math] ), co znaczy, że w punkcie [math]c\;[/math] funkcja [math]f\;[/math] ma minimum.
Załóżmy teraz, że [math]n\;[/math] jest liczbą nieparzystą. Niech [math]f^{(n)}(c)\lt 0\;[/math] (w przypadku przeciwnym, tzn. [math]f^{(n)}(c)\gt 0\;[/math], rozumowanie jest analogiczne). Weźmy znów [math]\delta\;[/math] takie, aby dla [math]|h|\lt \delta\;[/math] było [math]f^{(n)}(c+\theta h)\lt 0\;[/math]. Mamy wówczas dla [math]0\lt h\lt \delta\;[/math] nierówność
a dla [math]-\delta\lt h\lt 0\;[/math] zachodzi nierówność
tak więc w punkcie [math]c\;[/math] nie ma ani maksimum, ani minimum.
Przykład
Funkcja [math]f(x)=x^n\;[/math] posiada w [math]x=0\;[/math] minimum, jeśli [math]n\;[/math] jest parzyste i nie posiada minimum, jeśli [math]n\;[/math] jest nieparzyste.
Uwaga
Najczęściej spotyka się w zastosowaniach ekstrema niezdegenerowane, tzn. takie, że druga pochodna jest różna od zera. Wtedy testowanie, czy dany punkt krytyczny odpowiada ekstremum, kończy się na drugiej pochodnej.
Interpretacja geometryczna drugiej pochodnej. Punkty przegięcia
Uprzednio widzieliśmy, że jeśli [math]f'(c)\gt 0\;[/math], to funkcja rośnie w otoczeniu [math]c\;[/math]. Jeśli więc [math]f''(c)\gt 0\;[/math], to funkcja [math]f'\;[/math] rośnie; a jeśli ponadto [math]f'(c)\gt 0\;[/math], to [math]f\;[/math] rośnie jeszcze szybciej. To była heurystyka, a teraz
Twierdzenie
Jeśli druga pochodna funkcji [math]f\;[/math] jest ciągła i:
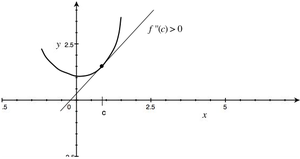
- zachodzi [math]f''(c)\gt 0\;[/math], to krzywa [math]y=f(x)\;[/math] jest dla pewnego otoczenia punktu [math]c\;[/math] położona powyżej stycznej do tej krzywej w punkcie [math](c,f(c)\;[/math] ;
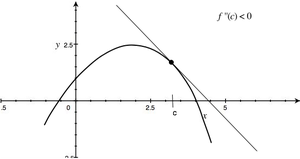
- zachodzi [math]f''(c)\lt 0\;[/math], to krzywa [math]y=f(x)\;[/math] jest dla pewnego otoczenia punktu [math]c\;[/math] położona poniżej stycznej do tej krzywej w punkcie [math](c,f(c)\;[/math].
Uwaga
Patrząc na wykres funkcji [math]f(x)\;[/math], widzimy, że w pierwszym przypadku wykres jest skierowany wypukłością do dołu, a w drugim — do góry.
Dowód
1. Oszacujmy różnicę między ilorazem różnicowym a pochodną:
Na mocy wzoru Taylora mamy:
Ponieważ [math]f''(c)\gt 0\;[/math], to dla dostatecznie małego [math]h\;[/math] mamy również
Interpretując iloraz różnicowy jako tangens kąta nachylenia siecznej do osi [math]OX\;[/math] wnioskujemy, że dla [math]h\gt 0\;[/math] tangens ten jest większy niż [math]f'(c)\;[/math], tzn. większy niż tg kąta między styczną a osią [math]OX\;[/math]. A to oznacza, że rozważana krzywa leży nad styczną, tak jak na rys. (3).
2. jest analogiczny.
Przykłady
- Parabola [math]y=x^2\;[/math] w każdym punkcie leży nad styczną — nic dziwnego, bo druga pochodna wszędzie jest tu równa 2.
- Wykres funkcji wykładniczej [math]y=e^x\;[/math] również leży wszędzie nad styczną — tak być musi, bo druga pochodna [math](e^x)''=e^x\gt 0\;[/math].
Punkt przegięcia
Rozważmy sytuację, gdy krzywa [math]y=f(x)\;[/math] posiada w punkcie [math]c\;[/math] styczną i dla dostatecznie małych przyrostów dodatnich krzywa leży po jednej strone stycznej (np. nad styczną), a dla dostatecznie małych przyrostów ujemnych leży po drugiej stronie
krzywej (np. pod krzywą). Innymi słowy: Rozpatrzmy wyrażenie:
i dla
dostatecznie małego [math]\delta\;[/math] mamy: [math]\forall_{0\lt h\lt \delta}\;[/math]: [math]\psi(h)\gt 0\;[/math] oraz [math]\forall_{-\delta\lt h\lt 0}\;[/math] : [math]\psi(h)\lt 0\;[/math].
W takiej sytuacji mówimy, że krzywa [math]y=f(x)\;[/math] ma punkcie [math]c\;[/math] punkt przegięcia.
Przykład
Sinusoida [math]y=\sin\; x\;[/math] ma punkt przegięcia dla [math]x=0\;[/math]. Mamy bowiem: [math]\psi(h)=\sin\; h -\sin\; 0 -h\cos\; 0 = \sin\; h-h\;[/math]. Dla [math]h\gt 0\;[/math] mamy [math]\psi(h)\lt 0\;[/math], dla [math]h\lt 0\;[/math] jest [math]\psi(h)\gt 0\;[/math].
Z tw. powyżej wynika, że jeśli [math]f''(c)\ne 0\;[/math], to krzywa leży (lokalnie) po jednej stronie stycznej. W takiej sytuacji, punkt [math]c\;[/math] nie jest punktem przegięcia. Możemy to sformułować jako
Twierdzenie
Jeśli punkt [math]c\;[/math] jest punktem przegięcia krzywej [math]y=f(x)\;[/math], to [math]f''(c)=0\;[/math]. Sytuacja odwrotna nie zachodzi (np. dla [math]y=x^4\;[/math] w [math]x=0\;[/math] ).
Funkcje wypukłe, wklęsłe i ich własności
Funkcje — wypukła i wklęsła
Funkcję [math]f:]a,b[\to \mathbb R \; \;[/math] nazywamy wypukłą na [math]]a,b[\;[/math], jeśli dla dowolnych [math]x,x'\in ]a,b[\;[/math] i [math]\theta\in [0,1]\;[/math] mamy rys.
zaś wklęsłą, jeśli
Wniosek
Funkcja [math]f\;[/math] jest wypukła wtedy i tylko wtedy, gdy funkcja [math]-f\;[/math] jest wklęsła. Wystarczy więc w dalszym ciągu zająć się tylko funkcjami wypukłymi.
Twierdzenie
Funkcja [math]f\;[/math] jest wypukła na [math]]a,b[\;[/math] wtedy i tylko wtedy, gdy dla dowolnego skończonego zbioru [math]n\;[/math] punktów [math]\{x_1, x_2, \dots, x_n\} \subset ]a,b[\;[/math] i dla dowolnego zestawu [math]n\;[/math] liczb [math]\theta_1, \dots, \theta_n\;[/math], takich, że [math]\theta_i\in [0,1]\;[/math], [math]i=1, \dots, n\;[/math] i [math]\sum_i \theta_i=1\;[/math], zachodzi
Dowód
indukcyjny. Niech [math]f\;[/math] będzie wypukła na [math]]a,b[\;[/math] — wtedy nierówność (16) zachodzi dla [math]n=2\;[/math].
Załóżmy, że teza jest prawdziwa dla [math]n-1\;[/math] (tzn. prawdziwa jest [math]T_{n-1}\;[/math].
Niech [math]\{x_1, x_2, \dots, x_n\} \subset ]a,b[\;[/math] i [math]0\leq \theta_i\leq 1\;[/math], [math]i=1, \dots, n\;[/math] będą takie, jak w sformułowaniu twierdzenia. Jeśli [math]\theta_n=1\;[/math], to nierówność jest trywialna. Weźmy więc [math]\theta_n\ne 1\;[/math]. Mamy:
a to znaczy, że prawdziwa jest [math]T_n\;[/math]. Udowodniliśmy więc implikację [math]T_{n-1}\Longrightarrow T_n\;[/math], czyli teza jest prawdziwa dla każdego [math]n\geq 2\;[/math].
W drugą stronę, dla [math]n=2\;[/math] mamy definicję funkcji wypukłej.
CBDO
Inne, równoważne kryteria wypukłości
Istnieją też inne równoważne kryteria wypukłości; użyteczne okaże się zaraz następujące stwierdzenie:
- [math]f\;[/math] jest wypukła [math]\Longleftrightarrow\;[/math] dla
dowolnych punktów [math]x_1\lt x_2\lt x_3\;[/math] z przedziału
[math]]a,b[\;[/math] spełniona jest nierówność
[math] \frac{f(x_2)-f(x_1)}{x_2-x_1}\leq \frac{f(x_2)-f(x_3)}{x_2-x_3}. [/math]
- [math]f\;[/math] jest wypukła [math]\Longleftrightarrow\;[/math] dla
dowolnych punktów [math]x_1\lt x_2\lt x_3\;[/math] z przedziału
[math]]a,b[\;[/math] spełniona jest nierówność
[math] \frac{f(x_3)-f(x_1)}{x_3-x_1}\leq \frac{f(x_3)-f(x_2)}{x_3-x_2}. [/math]
- [math]f\;[/math] jest wypukła [math]\Longleftrightarrow\;[/math] dla
dowolnych punktów [math]x_1\lt x_2\lt x_3\;[/math] z przedziału
[math]]a,b[\;[/math] spełniona jest nierówność
[math] \frac{f(x_2)-f(x_1)}{x_2-x_1}\leq \frac{f(x_3)-f(x_1)}{x_3-x_1}. \;[/math]
Dowód
Jeśli [math]x_1\lt x_2\lt x_3\;[/math], to [math]x_2=\theta x_1 + (1-\theta)x_3\;[/math], gdzie [math]\theta=\frac{x_3-x_2}{x_3-x_1}\;[/math] i [math]1-\theta=\frac{x_2-x_1}{x_3-x_1}\;[/math]. [math]f\;[/math] jest wypukła wtedy i tylko wtedy, gdy dla dowolnych punktów [math]x_1\lt x_2\lt x_3\;[/math] mamy nierówność
Ponieważ [math]{x_3-x_1}\;[/math], [math]{x_3-x_2}\;[/math] i [math]{x_2-x_1}\;[/math] są dodatnie, to nierówność (20) jest równoważna nierówności
czyli otrzymaliśmy (17).
Nierówność (20) można też zapisać w postaci
która jest równoważna nierówności
czyli otrzymaliśmy (18).
Wreszcie, gdy nierówność (20) zapiszemy w postaci
czyli otrzymaliśmy (19).
CBDO
Wniosek 1
Jeśli [math]f\;[/math] jest wypukła na [math]]a,b[\;[/math], to istnieją granice: lewo- i prawostronne pochodne:
Ponadto [math]f'_+ \geq f'_-\;[/math].
Dowód
Zauważmy, że funkcja [math]h\to \frac{f(x+h)-f(x)}{h}\;[/math] jest monotoniczna i ograniczona (powyższe Stw.), a stąd wynika istnienie granicy (podobnie jak dla ciągów).
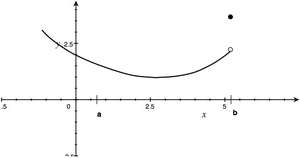
Wniosek 2
Funkcja wypukła na odcinku otwartym jest ciągła. Założenie otwartości odcinka jest istotne: Funkcja wypukła na odcinku domkniętym może być nieciągła na jego brzegu. (rys. (4))
Dla funkcji różniczkowalnych, mamy proste kryterium wypukłości.
Twierdzenie
- Funkcja różniczkowalna na [math]]a,b[\;[/math] jest wypukła [math]\Longleftrightarrow\;[/math] jej pochodna jest funkcją niemalejącą.
- Funkcja dwukrotnie różniczkowalna na [math]]a,b[\;[/math] jest wypukła [math]\Longleftrightarrow\;[/math] jej druga pochodna jest nieujemna.
Dowód
Widać, że drugi punkt wynika z pierwszego; wystarczy więc udowodnić pierwszy. Niech [math]x_1\lt x_2\lt x_3\;[/math] będą punktami w [math]]a,b[\;[/math]. Z tw. Lagrange'a istnieją [math]\xi\in ]x_1,x_2[\;[/math] oraz [math]\eta\in]x_2, x_3[\;[/math] takie, że [math]f(x_2)-f(x_1) = f'(\xi) (x_2-x_1)\;[/math] oraz [math]f(x_3)-f(x_2)=f'(\eta)(x_3-x_2)\;[/math]. Nierówność [math]f'(\eta)\geq f'(\xi)\;[/math] jest więc równoważna nierówności
Stąd powyższa nierówność jest spełniona dla wszystkich [math]x_1\lt x_2\lt x_3\;[/math] wtedy i tylko wtedy, gdy [math]f'\;[/math] jest funkcją niemalejącą. Ze Stw. wyżej wynika teza.
CBDO
Znaczenie wypukłości
Badanie funkcji: Kryteria na ekstremum, położenie stycznych do wykresu.
Termodynamika: Z wypukłości energii swobodnej wynika dodatniość takich (fizycznie oczywistych, ale trudnych bezpośrednio do udowodnienia) wielkości, jak ciepło właściwe: są to drugie pochodne en. sw. (tu: po temperaturze).
- ↑ Wzór ten daje się znacząco uogólnić na dowolne funkcje, dając tym samym sposób na przybliżenie dowolnej funkcji przez wielomian; zrobimy to już niedługo.