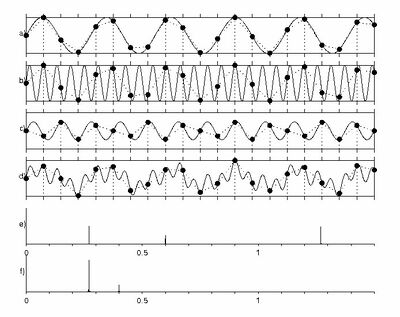
Aliasing: Różnice pomiędzy wersjami
| Linia 1: | Linia 1: | ||
==[[Analiza_sygnałów_-_lecture|AS/]] Przekształcenie Fouriera sygnałów dyskretnych, aliasing== | ==[[Analiza_sygnałów_-_lecture|AS/]] Przekształcenie Fouriera sygnałów dyskretnych, aliasing== | ||
| − | [[Media:aliasing.ogv|'''Kliknij na tym napisie aby obejrzeć animację pokazującą efekt aliasingu na sygnale jednowymiarowym''']] | + | ===[[Media:aliasing.ogv|'''Kliknij na tym napisie aby obejrzeć animację pokazującą efekt aliasingu na sygnale jednowymiarowym''']]=== |
| − | [[Plik:aliasingklatka.png]] | + | ===[[Media:aliasing.ogv|'''Kliknij na tym napisie aby obejrzeć animację pokazującą efekt aliasingu na sygnale jednowymiarowym''']]=== |
| + | |||
| + | [[Media:aliasing.ogv|Plik:aliasingklatka.png]] | ||
Przypomnijmy [[Przekształcenie Fouriera#label-eq:21|wzór na odwrotną transformację Fouriera]] sygnału ciągłego | Przypomnijmy [[Przekształcenie Fouriera#label-eq:21|wzór na odwrotną transformację Fouriera]] sygnału ciągłego | ||
Wersja z 12:15, 25 paź 2015
AS/ Przekształcenie Fouriera sygnałów dyskretnych, aliasing
Kliknij na tym napisie aby obejrzeć animację pokazującą efekt aliasingu na sygnale jednowymiarowym
Kliknij na tym napisie aby obejrzeć animację pokazującą efekt aliasingu na sygnale jednowymiarowym
Przypomnijmy wzór na odwrotną transformację Fouriera sygnału ciągłego [math] s(t)=\int_{-\infty}^{\infty}\hat{s}(f)e^{-i 2\pi t f} d f [/math]
Dyskretne wartości tego sygnału, próbkowane w chwilach [math]n \Delta t[/math], możemy odtworzyć z powyższgo równania dla [math]t = n \Delta t[/math]
[math] \sum_{r=-\infty}^\infty \int_\frac{(2r - 1)}{2\Delta t}^\frac{(2r + 1) }{2\Delta t} \hat{s}(f)e^{-i 2\pi n \Delta t f} d f \;\; \stackrel{f \rightarrow f+\frac{r}{\Delta t}}{=} \;\; [/math] [math] \sum_{r=-\infty}^\infty \int_\frac{-1}{2\Delta t}^\frac{1}{2\Delta t} \hat{s}\left(f + \frac{r}{\Delta t}\right)e^{-i 2\pi n \Delta t (f + \frac{r}{\Delta t})} d f [/math]
[math] = \int_\frac{-1}{2\Delta t}^\frac{1}{2\Delta t} \sum_{r=-\infty}^\infty \hat{s}\left(f + \frac{r}{\Delta t}\right)e^{-i 2\pi n \Delta t f} d f [/math]Szukając wartości sygnału w dyskretnych chwilach czasu, dostaliśmy w miejsce odwrotnej transformaty Fouriera całkę w ograniczonym zakresie z funkcji będącej (nieskończoną) sumą powtórzeń transformaty Fouriera sygnału ciągłego, przesuwanej o wielokrotności odwrotności [math]\Delta t[/math].
Innym sposobem pokazania tego efektu jest przedstawienie sekwencji dyskretnej [math]s[n][/math] jako iloczynu sygnału ciągłego [math]s(t)[/math] z grzebieniem Diraca
[math] D(t) = \sum_{k=-\infty}^{\infty} \delta(t-k\delta t) [/math]
Zgodnie z twierdzeniem o splocie, iloczyn w przestrzeni czasu będzie odpowiadał splotowi w dziedzinie częstości, czyli w dziedzinie częstości otrzymamy splot transformaty Fouriers sygnału [math]\hat{s}(t)[/math] z transformatą Fouriera grzebienia Diraca [math]\hat{D}(t)[/math], którą poniżej wyliczymy:
[math] \hat{D}(f) = \mathcal{F}(D(t)) = \mathcal{F}\left(\sum_{k=-\infty}^{\infty} \delta(t-k\Delta t) \right) = \int_{-\infty}^{\infty} \sum_{k=-\infty}^{\infty} \delta(t-k\Delta t) e^{i 2\pi f t} dt = [/math] [math] \sum_{k=-\infty}^{\infty} \int_{-\infty}^{\infty} \delta(t-k\Delta t) e^{i 2\pi f t} dt = \sum_{k=-\infty}^{\infty} e^{i 2\pi f k\Delta t} [/math]
Otrzymaliśmy ogólny wynik -- transformata Fouriera grzebienia Diraca to również grzebień Diraca (w przestrzeni częstości).
Przypomnijmy (np. z rozważań o systemach liniowych niezmienniczych w czasie), że splot z deltą Diraca w zerze jest identycznością, a splot z [math]\delta(t-kT)[/math] przesuwa funkcję o [math]kT[/math]. Z liniowości splotu dostajemy -- jak pozyżej -- sumę powtórzeń transformaty Fouriera sygnału ciągłego, przesuwanej o wielokrotności odwrotności [math]\Delta t[/math].