Uczenie maszynowe i sztuczne sieci neuronowe/Ćwiczenia 4: Różnice pomiędzy wersjami
| (Nie pokazano 6 wersji utworzonych przez 2 użytkowników) | |||
| Linia 1: | Linia 1: | ||
| + | [[Uczenie_maszynowe_i_sztuczne_sieci_neuronowe_cw]]/Wsteczna propagacja błędu | ||
=Algorytm wstecznej propagacji błędu= | =Algorytm wstecznej propagacji błędu= | ||
W tym ćwiczeniu zapoznamy się z algorytmem wstecznej propagacji błędu. Zbudujemy sieć złożoną z 3 warstw: wejściowej, ukrytej i wyjściowej. | W tym ćwiczeniu zapoznamy się z algorytmem wstecznej propagacji błędu. Zbudujemy sieć złożoną z 3 warstw: wejściowej, ukrytej i wyjściowej. | ||
| Linia 37: | Linia 38: | ||
* przygotuj zbiór uczący zgodnie z powyższą tabelą. Niech przykłady będą ułożone w wierszach tablic X i Y | * przygotuj zbiór uczący zgodnie z powyższą tabelą. Niech przykłady będą ułożone w wierszach tablic X i Y | ||
* zdefiniuj rozmiary sieci: | * zdefiniuj rozmiary sieci: | ||
| − | **N_wej | + | ** N_wej |
** N_hid | ** N_hid | ||
** N_wyj | ** N_wyj | ||
| Linia 43: | Linia 44: | ||
** jakie rozmiary muszą mieć te tablice? | ** jakie rozmiary muszą mieć te tablice? | ||
** zainicjuj je wartościami losowymi z przedziału -1,1 | ** zainicjuj je wartościami losowymi z przedziału -1,1 | ||
| + | * podobnie przygotuj tablicę dla wag w_2 | ||
* w pętli wykonuj kolejne cykle uczenia | * w pętli wykonuj kolejne cykle uczenia | ||
** zainicjuj do zera: licznik błędu wyjściowego bl, oraz tablice akumulujące delty do zmiany wag D_1 i D_2 | ** zainicjuj do zera: licznik błędu wyjściowego bl, oraz tablice akumulujące delty do zmiany wag D_1 i D_2 | ||
| Linia 60: | Linia 62: | ||
** wypisujemy info o błędzie | ** wypisujemy info o błędzie | ||
| + | ==Po zakodowaniu uczenia == | ||
| + | |||
| + | * Proszę wykreślić ewolucje wag i błędu. Ewolucję można zilustrować animacją. W tym celu na początku programu należy ustawić backend dla biblioteki matplotlib przed innymi importami i przełączyć grafikę w tryb interaktywny: | ||
| + | <source lang = python> | ||
| + | import matplotlib | ||
| + | matplotlib.use('TkAgg') | ||
| + | import pylab as py | ||
| + | py.ion() | ||
| + | </source> | ||
| + | Następnie animację robimy analogicznie jak [[TI/Matplotlib#Prosta_animacja| w tym przykładzie.]] | ||
| + | |||
| + | * Proszę zbadać co dzieje się z wagami wraz ze wzrostem ilości jednostek w warstwie ukrytej. | ||
| + | * Proszę powtórzyć analizę dla sieci, której warstwa wyjściowa ma jednostkę liniową. | ||
| + | |||
| + | == Szkielet rozwiązania== | ||
| + | <source lang = python> | ||
| + | # -*- coding: utf-8 -*- | ||
| + | import numpy as np | ||
| + | |||
| + | def g(x): | ||
| + | y = ... | ||
| + | return y | ||
| + | |||
| + | def g_prim(x): | ||
| + | y = ... | ||
| + | return y | ||
| + | |||
| + | |||
| + | #zbiór uczący: | ||
| + | # wejście, | ||
| + | X = np.array([ [0,0], | ||
| + | [0,1], | ||
| + | [1,0], | ||
| + | [1,1] ]) | ||
| + | |||
| + | # wyjście | ||
| + | Y = np.array([[0,1], | ||
| + | [1,0], | ||
| + | [1,0], | ||
| + | [0,1]]) | ||
| + | |||
| + | |||
| + | # definiujemy rozmiary sieci: | ||
| + | N_wej = ... | ||
| + | N_hid = 3 | ||
| + | N_wyj = ... | ||
| + | |||
| + | # inicjujemy połączenia | ||
| + | # wagi ułożone są tak, że w kolejnych wierszach są kolejne neurony | ||
| + | # a w kolumnach wagi od konkretnego neuronu | ||
| + | # to +1 jest wagą dla obciążenia | ||
| + | w_1 = 2*np.random.random((...)) - ... # pomiędzy warstwą pierwszą (wejściem) a warstwą ukrytą | ||
| + | w_2 = 2*np.random.random((...)) - ... | ||
| + | |||
| + | |||
| + | for cykl in range(10000): | ||
| + | bl =0 | ||
| + | D_1 = np.zeros((...)) | ||
| + | D_2 = np.zeros((...)) | ||
| + | |||
| + | |||
| + | for i in range(0,4): | ||
| + | # weźmy przykład i-ty | ||
| + | |||
| + | x = X[i,:].reshape(...) | ||
| + | y = Y[i,:].reshape(...) | ||
| + | |||
| + | # propagacja "w przód" | ||
| + | a_0 = np.vstack((1,x)) # z warstwy wejściowej (zerowej) wychodzi a_0 | ||
| + | |||
| + | z_1 = np.dot( w_1, a_0 )# na warstwe 1 wchodzą iloczyny skalarne | ||
| + | a_1 = np.vstack((1,g(z_1))) # dokładamy 1 i dostaję wyjście z warstwy 1 | ||
| + | |||
| + | z_2 = np.dot( ... ) # na warstwe 3 wchodzą iloczyny skalarne | ||
| + | a_2 = g(...) | ||
| + | if cykl == 10000-1: | ||
| + | print 'a: ',str(a_2.T) | ||
| + | print 'y: ',str(y.T) | ||
| + | # propagacja "wstecz" | ||
| + | d_2 = (...)*g_prim(a_2) | ||
| + | d_1 = np.dot(...) * g_prim(a_1) | ||
| + | |||
| + | # akumulujemy poprawki | ||
| + | D_2 += np.dot( ...) | ||
| + | D_1 += np.dot( ...) | ||
| + | |||
| + | bl += np.dot(...) | ||
| + | |||
| + | eta1 = 0.1 | ||
| + | # uaktualniamy wagi | ||
| + | w_1 -= eta1*D_1 | ||
| + | w_2 -= ... | ||
| + | |||
| + | # wypisujemy info o błędzie | ||
| + | if (cykl% 1000) == 0: | ||
| + | print 'bl: ', bl | ||
| + | </source> | ||
| + | |||
| + | |||
| + | <!-- | ||
| + | {{hidden begin|title=przykładowy kod}} | ||
| + | <source lang = python> | ||
| + | # -*- coding: utf-8 -*- | ||
| + | import numpy as np | ||
| + | |||
| + | def g(x): | ||
| + | y = 1./(1+np.exp(-x)) | ||
| + | return y | ||
| + | |||
| + | def g_prim(x): | ||
| + | y = x*(1-x) | ||
| + | return y | ||
| + | |||
| + | |||
| + | #zbiór uczący: | ||
| + | # wejście, | ||
| + | X = np.array([ [0,0], | ||
| + | [0,1], | ||
| + | [1,0], | ||
| + | [1,1] ]) | ||
| + | |||
| + | # wyjście | ||
| + | Y = np.array([[0,1], | ||
| + | [1,0], | ||
| + | [1,0], | ||
| + | [0,1]]) | ||
| + | |||
| + | |||
| + | # definiujemy rozmiary sieci: | ||
| + | N_wej = X.shape[1] | ||
| + | N_hid = 3 | ||
| + | N_wyj = Y.shape[1] | ||
| + | |||
| + | # inicjujemy połączenia | ||
| + | # wagi ułożone są tak, że w kolejnych wierszach są kolejne neurony | ||
| + | # a w kolumnach wagi od konkretnego neuronu | ||
| + | # to +1 jest wagą dla obciążenia | ||
| + | w_1 = 2*np.random.random((N_hid, N_wej+1)) - 1# pomiędzy warstwą pierwszą (wejściem) a warstwą ukrytą | ||
| + | w_2 = 2*np.random.random((N_wyj, N_hid+1)) - 1 | ||
| + | |||
| + | |||
| + | for cykl in range(10000): | ||
| + | bl =0 | ||
| + | D_1 = np.zeros((N_hid,N_wej+1)) | ||
| + | D_2 = np.zeros((N_wyj,N_hid+1)) | ||
| + | |||
| + | |||
| + | for i in range(0,4): | ||
| + | # weźmy przykład i-ty | ||
| + | |||
| + | x = X[i,:].reshape(X.shape[1],1) | ||
| + | y = Y[i,:].reshape(Y.shape[1],1) | ||
| + | |||
| + | # propagacja "w przód" | ||
| + | a_0 = np.vstack((1,x)) # z warstwy wejściowej (zerowej) wychodzi a_0 | ||
| + | |||
| + | z_1 = np.dot( w_1, a_0 )# na warstwe 1 wchodzą iloczyny skalarne | ||
| + | a_1 = np.vstack((1,g(z_1))) # dokładamy 1 i dostaję wyjście z warstwy 1 | ||
| + | |||
| + | z_2 = np.dot( w_2, a_1 ) # na warstwe 3 wchodzą iloczyny skalarne | ||
| + | a_2 = g(z_2) | ||
| + | if cykl == 10000-1: | ||
| + | print 'a: ',str(a_2.T) | ||
| + | print 'y: ',str(y.T) | ||
| + | # propagacja "wstecz" | ||
| + | d_2 = (a_2 - y)*g_prim(a_2) | ||
| + | d_1 = np.dot(w_2.T, d_2) * g_prim(a_1)#z_2 | ||
| + | |||
| + | # akumulujemy poprawki | ||
| + | D_2 += np.dot( d_2, a_1.T) | ||
| + | D_1 += np.dot( d_1[1:], a_0.T) | ||
| + | |||
| + | bl += np.dot(d_2.T,d_2) | ||
| + | |||
| + | eta1 = 0.1 | ||
| + | # uaktualniamy wagi | ||
| + | w_1 -= eta1*D_1 | ||
| + | w_2 -= eta1*D_2 | ||
| + | |||
| + | # wypisujemy info o błędzie | ||
| + | if (cykl% 1000) == 0: | ||
| + | print 'bl: ', bl | ||
| + | </source> | ||
| + | {{hidden end}} | ||
| + | --> | ||
| + | <!-- | ||
=XOR= | =XOR= | ||
Jako pierwszy przykład z zastosowania sieci nieliniowych proszę skonstruować sieć z jedną warstwą ukrytą, rozwiązującą problem XOR. | Jako pierwszy przykład z zastosowania sieci nieliniowych proszę skonstruować sieć z jedną warstwą ukrytą, rozwiązującą problem XOR. | ||
| Linia 217: | Linia 405: | ||
--> | --> | ||
| + | |||
| + | [[Uczenie_maszynowe_i_sztuczne_sieci_neuronowe_cw]]/Wsteczna propagacja błędu | ||
Aktualna wersja na dzień 06:46, 23 maj 2017
Uczenie_maszynowe_i_sztuczne_sieci_neuronowe_cw/Wsteczna propagacja błędu
Algorytm wstecznej propagacji błędu
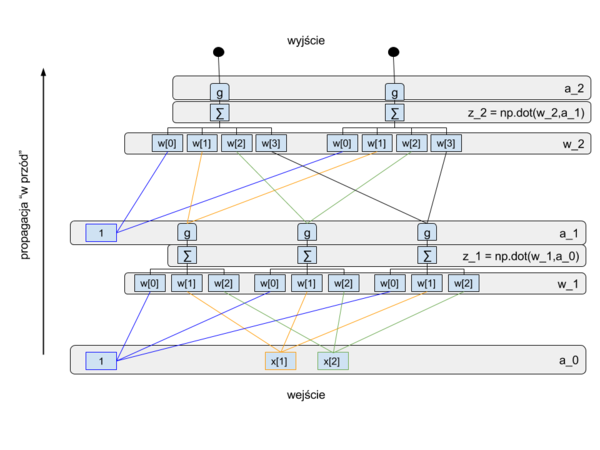
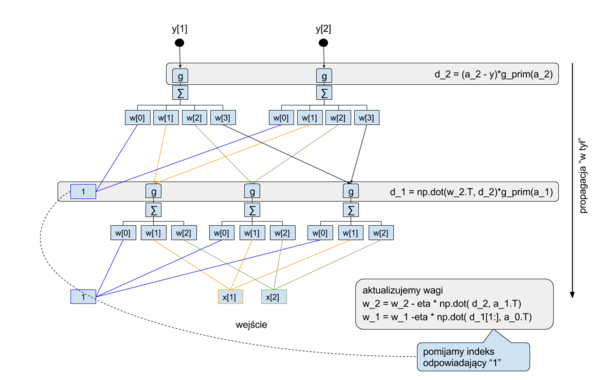
W tym ćwiczeniu zapoznamy się z algorytmem wstecznej propagacji błędu. Zbudujemy sieć złożoną z 3 warstw: wejściowej, ukrytej i wyjściowej. Schemat obliczeń wykonywanych przez tą sieć przedstawiony jest na poniższych rysunkach:
Warstwy ukryta i wyjściowa będą miały nieliniową funkcję aktywacji w postaci funkcji logistycznej. Dla przypomnienia funkcja logistyczna:
- [math]g(x) = \frac{1}{1+exp(-x)}[/math]
zaś jej pochoną to:
- [math]g'(x) =g(x)*(1-g(x)) [/math]
Niech nasza sieć uczy się odwzorowania zadanego tabelką:
| X | Y |
|---|---|
| [0,0] | [0,1] |
| [0,1] | [1,0] |
| [1,0] | [1,0] |
| [1,1] | [0,1] |
Proszę napisać kod implementujący obliczenia przedstawione na rysunkach i w poniższym opisie:
- zdefiniuj funkcję g(x)
- zdefiniuj funkcję pochodną g_prim(y), zakładając, że jako argument y podawać będziemy wartość g(x)
- przygotuj zbiór uczący zgodnie z powyższą tabelą. Niech przykłady będą ułożone w wierszach tablic X i Y
- zdefiniuj rozmiary sieci:
- N_wej
- N_hid
- N_wyj
- przygotuj tablicę do przechowywania wag w_1, niech w kolejnych wierszach znajdują się wagi kolejnych neuronów, a w konkretnym wierszu w kolumnach kolejne wagi od konkretnego neuronu
- jakie rozmiary muszą mieć te tablice?
- zainicjuj je wartościami losowymi z przedziału -1,1
- podobnie przygotuj tablicę dla wag w_2
- w pętli wykonuj kolejne cykle uczenia
- zainicjuj do zera: licznik błędu wyjściowego bl, oraz tablice akumulujące delty do zmiany wag D_1 i D_2
- w pętli pobieraj kolejno przykłady. Pobierając przykłady formuj je jako wektory kolumnowe
- propaguj sygnały od wejścia:
- uzupełnij wektor wejściowy o "1" na szczycie, wsk. np.vstack)
- oblicz pobudzenia neuronów z_1,
- oblicz wartości wyjściowe z warstwy ukrytej
- uzupełnij wektor wartości wyjściowych warstwy ukrytej o "1"
- oblicz pobudzenia w warstwie wyjściowej
- oblicz wartości wyjściowe z tej warstwy
- propaguj błędy "wstecz"
- oblicz błąd warstwy wyjściowej ważony przez pochodną funkcji g (im bardziej funkcja g była stroma w miejscu pobudzenia przy propagacji wprzód, tym bardziej błąd pobudzenia przekładał się na błąd wyjścia)
- zrzutuj ten błąd wstecz poprzez wagi w_2 i pochodną funkcji g
- akumulujemy poprawki D_1 i D_2 oraz błąd dla tego przykładu
- propaguj sygnały od wejścia:
- uaktualniamy wagi proporcjonalnie do poprawek (z przeciwnym znakiem)
- wypisujemy info o błędzie
Po zakodowaniu uczenia
- Proszę wykreślić ewolucje wag i błędu. Ewolucję można zilustrować animacją. W tym celu na początku programu należy ustawić backend dla biblioteki matplotlib przed innymi importami i przełączyć grafikę w tryb interaktywny:
import matplotlib
matplotlib.use('TkAgg')
import pylab as py
py.ion()
Następnie animację robimy analogicznie jak w tym przykładzie.
- Proszę zbadać co dzieje się z wagami wraz ze wzrostem ilości jednostek w warstwie ukrytej.
- Proszę powtórzyć analizę dla sieci, której warstwa wyjściowa ma jednostkę liniową.
Szkielet rozwiązania
# -*- coding: utf-8 -*-
import numpy as np
def g(x):
y = ...
return y
def g_prim(x):
y = ...
return y
#zbiór uczący:
# wejście,
X = np.array([ [0,0],
[0,1],
[1,0],
[1,1] ])
# wyjście
Y = np.array([[0,1],
[1,0],
[1,0],
[0,1]])
# definiujemy rozmiary sieci:
N_wej = ...
N_hid = 3
N_wyj = ...
# inicjujemy połączenia
# wagi ułożone są tak, że w kolejnych wierszach są kolejne neurony
# a w kolumnach wagi od konkretnego neuronu
# to +1 jest wagą dla obciążenia
w_1 = 2*np.random.random((...)) - ... # pomiędzy warstwą pierwszą (wejściem) a warstwą ukrytą
w_2 = 2*np.random.random((...)) - ...
for cykl in range(10000):
bl =0
D_1 = np.zeros((...))
D_2 = np.zeros((...))
for i in range(0,4):
# weźmy przykład i-ty
x = X[i,:].reshape(...)
y = Y[i,:].reshape(...)
# propagacja "w przód"
a_0 = np.vstack((1,x)) # z warstwy wejściowej (zerowej) wychodzi a_0
z_1 = np.dot( w_1, a_0 )# na warstwe 1 wchodzą iloczyny skalarne
a_1 = np.vstack((1,g(z_1))) # dokładamy 1 i dostaję wyjście z warstwy 1
z_2 = np.dot( ... ) # na warstwe 3 wchodzą iloczyny skalarne
a_2 = g(...)
if cykl == 10000-1:
print 'a: ',str(a_2.T)
print 'y: ',str(y.T)
# propagacja "wstecz"
d_2 = (...)*g_prim(a_2)
d_1 = np.dot(...) * g_prim(a_1)
# akumulujemy poprawki
D_2 += np.dot( ...)
D_1 += np.dot( ...)
bl += np.dot(...)
eta1 = 0.1
# uaktualniamy wagi
w_1 -= eta1*D_1
w_2 -= ...
# wypisujemy info o błędzie
if (cykl% 1000) == 0:
print 'bl: ', bl
Uczenie_maszynowe_i_sztuczne_sieci_neuronowe_cw/Wsteczna propagacja błędu