Ćwiczenia 1: Różnice pomiędzy wersjami
| (Nie pokazano 51 wersji utworzonych przez 7 użytkowników) | |||
| Linia 1: | Linia 1: | ||
| − | == Dokumentacja modułu scipy.signal == | + | [[Analiza_sygnałów_-_ćwiczenia]]/Sygnały |
| + | |||
| + | ==Narzędzia wykorzystywane na ćwiczeniach== | ||
| + | ===Python=== | ||
| + | |||
| + | Python jest językiem programowania wysokiego poziomu, który w połączeniu z bibliotekami NumPy i SciPy do obliczeń naukowych pozwala na szybkie i wygodne programowanie lub analizowanie danych w sposób interaktywny. Przykłady prezentowane w ramach zajęć powinny uruchamiać się zarówno w wersji 2 jak i 3 języka Python, jednak zachęcamy Państwa, aby od początku uczyć się i korzystać z wersji 3 języka. | ||
| + | |||
| + | Szczególnie przydatne na analizie sygnałów będą moduły: | ||
| + | *numpy | ||
| + | *scipy | ||
| + | *matplotlib | ||
| + | |||
| + | Do reprezentowania sygnałów w programach będziemy stosować tablice numpy: | ||
| + | * <tt>ndarray</tt> | ||
| + | Jest to zarówno efektywne jeśli chodzi o pamięć jak i o szybkość wykonywania operacji matematycznych. | ||
| + | |||
| + | ==== Dokumentacja modułu scipy.signal ==== | ||
Proszę zapoznać się z dokumentacją biblioteki scipy.signal: | Proszę zapoznać się z dokumentacją biblioteki scipy.signal: | ||
| − | + | https://docs.scipy.org/doc/scipy/reference/ | |
| + | |||
| + | ===Svarog=== | ||
| + | Przydatnym narzędziem do analizy sygnałów, z którego będziemy korzystać na zajęciach, jest program SVAROG (pierwotnie skrót od Signal Viewer, Analyzer and Recorder On GPL). Program działa w środowisku Java, jest więc niezależny od systemu operacyjnego (Linux, Windows, OS X…). Svarog pozwala na wczytywanie i analizowanie sygnałów (nie tylko bioelektrycznych), zarówno przy użyciu prostych (FFT, spektrogram) jak i bardziej zaawansowanych (matching pursuit, ICA, DTF itd.) narzędzi. Dzięki współpracy z platformą OpenBCI, możliwa jest rejestracja sygnału (łącznie z metadanymi) bezpośrednio z poziomu graficznego interfejsu użytkownika. | ||
| + | |||
| + | ====Svarog: uruchamianie i konfiguracja==== | ||
| + | Aktualną wersję programu Svarog można pobrać [http://braintech.pl/svarog/]. Program nie wymaga instalacji. Po rozpakowaniu paczki do dowolnego katalogu należy uruchomić skrypt „run-svarog.sh” lub uruchomić bezpośrednio plik *.jar. | ||
| + | |||
| + | Aktualnie najnowsza wersja jest tutaj: https://gitlab.com/fuw_software/svarog2-packager/-/releases :) | ||
| + | |||
| + | |||
| + | W przypadku pracy na własnych komputerach, do prawidłowego uruchomienia pluginu do analizy sygnałów, z którego będziemy korzystać w dalszej części ćwiczeń, konieczne jest zainstalowanie środowiska Oracle Java SE w wersji 8, które można pobrać [http://www.oracle.com/technetwork/java/javase/downloads/index.html ze strony wydawcy]. Alternatywnie, użytkownicy systemu Ubuntu lub pokrewnych dystrybucji mogą zainstalować środowisko Java według instrukcji [http://www.webupd8.org/2012/09/install-oracle-java-8-in-ubuntu-via-ppa.html dostępnych na tej stronie]. | ||
==Sygnały ciągłe i dyskretne == | ==Sygnały ciągłe i dyskretne == | ||
===Próbkowanie w czasie === | ===Próbkowanie w czasie === | ||
| − | + | W tym ćwiczeniu zilustrujemy pojęcia: | |
* częstość próbkowania | * częstość próbkowania | ||
* częstość Nyquista | * częstość Nyquista | ||
* aliasing | * aliasing | ||
| − | W poniższym ćwiczeniu chcemy zbadać efekt próbkowania sygnału w czasie. W komputerach nie mamy dostępu do sygnału ciągłego. | + | ====Zadanie 1: Próbkowanie==== |
| + | W poniższym ćwiczeniu chcemy zbadać efekt próbkowania sygnału w czasie. | ||
| + | *W komputerach nie mamy dostępu do sygnału ciągłego. | ||
| + | *Wartości sygnału znane są tylko w dyskretnych momentach czasu. | ||
| + | *Najczęściej stosujemy równe odstępy czasu <math>dt</math> | ||
| + | *Odwrotność tych okresów to częstość próbkowania <math>Fs = \frac{1}{dt}</math> | ||
| + | *Bardzo wygodnie jest myśleć o sygnałach jako o wektorach lub macierzach (rys. na tablicy) | ||
| + | *Do przechowywania sygnałów w pamięci używamy ndarray | ||
| − | |||
| + | Czy próbkując sygnał z częstością <math>Fs = 100</math>[Hz] mogę odwzorować sygnał o dowolnej częstości? | ||
| + | * wytwórz wektor t reprezentujący czas 1s próbkowany z częstością Fs | ||
<source lang =python> | <source lang =python> | ||
# -*- coding: utf-8 -*- | # -*- coding: utf-8 -*- | ||
| Linia 20: | Linia 55: | ||
import pylab as py | import pylab as py | ||
import numpy as np | import numpy as np | ||
| − | + | Fs =100 | |
| − | t = np.arange(0,1, | + | dt = 1/Fs |
| + | t = np.arange(0,1,dt) # czas 'prawie ciągły' | ||
</source> | </source> | ||
| − | + | * wytwórz sygnał s, sinus o częstości f =10Hz. Dla przypomnienia wyrażenie: <math> s(t) = \sin(2 \pi f t)</math> możemy w pythonie zapisać: | |
| − | :<math> s(t) = \sin(2 \pi f t)</math> możemy w pythonie zapisać: | ||
<source lang =python> | <source lang =python> | ||
s = np.sin(2*np.pi*f*t) | s = np.sin(2*np.pi*f*t) | ||
</source> | </source> | ||
| − | + | * wykreśl ten sygnał za pomocą punktów i linii | |
| + | * wykreśl sygnały o częstościach 20, 40, 50, 90 Hz | ||
| − | Teraz proszę spróbkować czas i nasze „prawie” ciągłe sinusoidy z okresem próbkowania 0,1. (Trzeba pobrać co 100 element, proszę posłużyć się [[Programowanie_z_Pythonem/Sekwencje#Wycinki|wycinkami]]) <!-- [[TI/Sekwencje|Struktury danych — sekwencje|wycinkami]]. --> | + | ====Efekt aliasingu==== |
| − | Na tle „prawie” ciągłych sinusoid proszę dorysować punkty ze spróbkowanych sygnałów. Aby punkty były dobrze widoczne proponuję użyć markerów <tt>x</tt> oraz <tt>+</tt>. | + | Rzućmy okiem na przykład tego efektu: https://youtu.be/SFbINinFsxk |
| − | + | * koła obracają się z pewną częstością zgodnie z kierunkiem ruchu wskazówek zegara; | |
| − | Proszę zaobserwować wzajemne położenie punktów. Czy można odróżnić sinusoidę o częstości −1 od sinusoidy o częstości 9, jeśli obie są próbkowane z częstością 10? Jak można uogólnić tą obserwację? | + | * na filmie widać, że w pewnych kierunek ten się zmienia, mimo, że samochód wciąż jedzie w tą samą stronę; |
| − | + | * możemy przyjąć umownie, że obrotom zgodnie z kierunkiem wskazówek zegara przypiszemy wartości dodatnie, a obrotom w kierunku przeciwnym wartości ujemne. | |
| + | * Dlaczego tak się dzieje? | ||
| + | Analogiczne zjawisko przeanalizujemy dla symulowanych sygnałów okresowych. | ||
| + | Na nasze potrzeby wygenerujemy sygnały próbkowane z bardzo dużą częstością, które będą dla nas aproksymacją sygnałów ciągłych. Przy ich pomocy zaprezentujemy efekt utożsamiania (aliasingu). | ||
| + | *Proszę wytworzyć wektor reprezentujący czas „prawie” ciągły. Będzie to u nas 1000 wartości z przedziału [0,1) wziętych z odstępem 0,001. | ||
| + | *Teraz proszę wygenerować dwie sinusoidy: jedną o częstości <tt>-1</tt> a drugą o częstości <tt>9</tt>. | ||
| + | *Proszę [[TI/Matplotlib#Kilka_wykres.C3.B3w_we_wsp.C3.B3lnych_osiach|wykreślić]] obie sinusoidy. | ||
| + | *Teraz proszę spróbkować czas i nasze „prawie” ciągłe sinusoidy z okresem próbkowania 0,1. (Trzeba pobrać co 100 element, proszę posłużyć się [[Programowanie_z_Pythonem/Sekwencje#Wycinki|wycinkami]]) <!-- [[TI/Sekwencje|Struktury danych — sekwencje|wycinkami]]. --> | ||
| + | *Na tle „prawie” ciągłych sinusoid proszę dorysować punkty ze spróbkowanych sygnałów. Aby punkty były dobrze widoczne proponuję użyć markerów <tt>x</tt> oraz <tt>+</tt>. | ||
| + | *Proszę zaobserwować wzajemne położenie punktów. | ||
| + | *Czy można odróżnić sinusoidę o częstości −1 od sinusoidy o częstości 9, jeśli obie są próbkowane z częstością 10? | ||
| + | *Jak można uogólnić tą obserwację? | ||
| + | |||
| + | <tt>*</tt> | ||
<!-- | <!-- | ||
# -*- coding: utf-8 -*- | # -*- coding: utf-8 -*- | ||
| Linia 170: | Linia 219: | ||
</source> | </source> | ||
=== Przykład: eksport sygnału do pliku binarnego === | === Przykład: eksport sygnału do pliku binarnego === | ||
| + | *Przypominamy: | ||
| + | ** dtype http://docs.scipy.org/doc/numpy/reference/arrays.dtypes.html#arrays-dtypes-constructing | ||
| + | ** open/close | ||
| + | ** tofile | ||
| + | ** fromfile | ||
| + | |||
* Poniższy kod ilustruje sposób zapisu dwóch funkcji sinus o częstościach 10 Hz i 21 Hz do pliku binarnego: | * Poniższy kod ilustruje sposób zapisu dwóch funkcji sinus o częstościach 10 Hz i 21 Hz do pliku binarnego: | ||
| Linia 177: | Linia 232: | ||
import numpy as np | import numpy as np | ||
| − | + | T = 5 | |
| − | + | Fs = 128 | |
| − | |||
| − | + | (s1,t) = sin(f=10, T=T, Fs=Fs) | |
| − | + | (s2,t) = sin(f=21, T=T, Fs=Fs) | |
| − | + | ||
| − | + | signal = np.zeros((T*Fs, 2), dtype='<f') | |
| − | + | signal[:, 0] = s1 | |
| − | + | signal[:, 1] = s2 | |
| − | + | # zapis sygnału binarnego: | |
| − | + | f_out = open('test_signal1.bin', 'wb') # otwieramy plik do pisania binarnego: 'wb' | |
| + | signal.tofile(f_out) # zrzucamy zawartość tablicy ''signal'' do pliku identyfikowanego przez ''f_out'' | ||
| + | f_out.close() # zamykamy plik | ||
| + | # czynność odwrotna - wczytanie sygnału binarnego | ||
| + | ch = 2 # liczba kanałów | ||
| + | fin = open('test_signal1.bin', 'rb') # otwieramy plik do czytania binarnego: 'rb' | ||
| + | s = np.fromfile(fin, dtype='<f') # tworzymy tablicę sig o typie określonym przez ''dtype'' | ||
| + | # wkładając do niej bity z pliku ''fin'' interpretowane zgodnie z ''dtype'' | ||
| + | fin.close() # zamykamy plik | ||
| + | s = np.reshape(s,(len(s)/ch,ch)) # zmieniamy tablicę z jednowymiarowej na dwuwymiarową | ||
</source> | </source> | ||
| Linia 197: | Linia 260: | ||
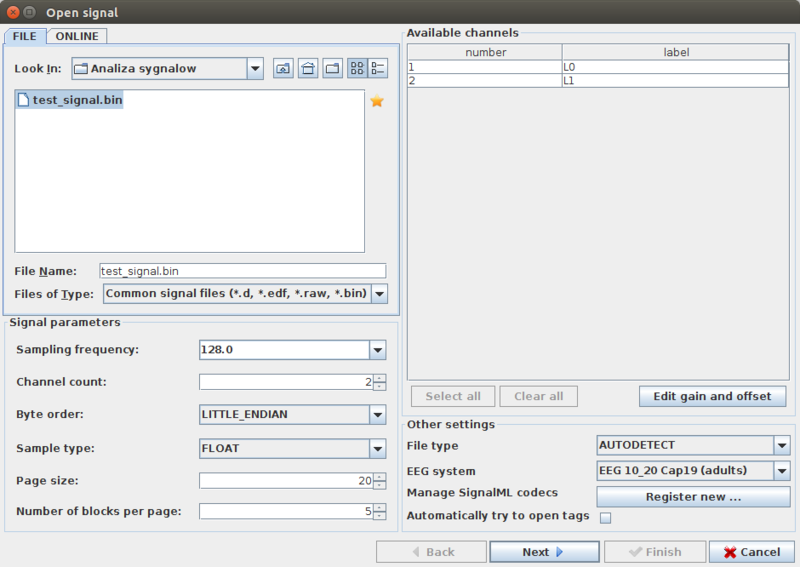
[[Plik:svarog_open_signal.png|center|800px|thumb|<figure id="uid3" />Wczytywanie sygnału w programie Svarog.]] | [[Plik:svarog_open_signal.png|center|800px|thumb|<figure id="uid3" />Wczytywanie sygnału w programie Svarog.]] | ||
| + | |||
| + | === Zadanie 2: Nieznany typ danych=== | ||
| + | Posiadamy 3 kanałowy plik binarny z sygnałem EEG. Niestety zapomnieliśmy jaki jest typ zapisanych danych. Proszę wczytać plik i przy pomocy biblioteki matplotlib oraz grafik z fragmentami sygnałów odgadnąć, która z pośród wymienionych zmiennych dtype jest prawdziwa: | ||
| + | <ul> | ||
| + | <li> 'float32' | ||
| + | |||
| + | <li> '>H' | ||
| + | |||
| + | <li> 'uint64' | ||
| + | |||
| + | <li> 'float64' | ||
| + | </ul> | ||
| + | Plik binarny oraz grafiki można pobrać z [https://drive.google.com/drive/folders/0ByBe6Y9KQQXYRnVVQVhtdnJkWHM?usp=sharing stąd] | ||
| + | |||
| + | === Zadanie 3: Nieznana liczba kanałów=== | ||
| + | Posiadamy n kanałowy plik binarny z sygnałem EKG, EEG i EMG, typ zmiennej to '<f'. Niestety zapomnieliśmy jaka jest liczba kanałów. Proszę wczytać plik i przy pomocy biblioteki matplotlib oraz grafik z fragmentami sygnałów odgadnąć liczbę kanałów. Plik binarny oraz grafiki można pobrać z [https://drive.google.com/drive/folders/0ByBe6Y9KQQXYVFpOV3A4ZllYUGc?usp=sharing stąd] | ||
| + | |||
| + | === Zadanie 4:=== | ||
| + | Proszę stworzyć nową macierz z n+3 kanałami, zawierającą sygnały z dwóch poprzednich zadań. Następnie proszę zapisać macierz sygnałów do pliku binarnego i otworzyć w programie Svarog. | ||
=== Delta === | === Delta === | ||
| Linia 212: | Linia 294: | ||
</source> | </source> | ||
| − | === Zadanie:=== | + | === Zadanie 5:=== |
| − | Analogicznie do powyższych przykładów proszę zaimplementować | + | Analogicznie do powyższych przykładów proszę zaimplementować i przetestować funkcje generujące: |
* funkcję Gabora (funkcja Gaussa modulowana cosinusem) o zadanej częstości i standardowym odchyleniu w czasie, momencie wystąpienia, długości, częstości próbkowania i fazie. | * funkcję Gabora (funkcja Gaussa modulowana cosinusem) o zadanej częstości i standardowym odchyleniu w czasie, momencie wystąpienia, długości, częstości próbkowania i fazie. | ||
:<math> g = \exp\left(-\frac{1}{2}\left(\frac{t-t_0}{\sigma}\right)^2 \right) \cdot \cos(2 \pi f t + \phi); </math> | :<math> g = \exp\left(-\frac{1}{2}\left(\frac{t-t_0}{\sigma}\right)^2 \right) \cdot \cos(2 \pi f t + \phi); </math> | ||
| Linia 219: | Linia 301: | ||
* szum gaussowski o zadanej średniej, odchyleniu standardowym, długości i częstości próbkowania. | * szum gaussowski o zadanej średniej, odchyleniu standardowym, długości i częstości próbkowania. | ||
| − | * pochodną funkcji Gaussa | + | <!-- * pochodną funkcji Gaussa |
* połówkę funkcji Gaussa | * połówkę funkcji Gaussa | ||
| + | --> | ||
| + | |||
| + | ==Co musimy z tego zapamiętać? == | ||
| + | * sygnały dyskretne - dyskretne chwile czasu | ||
| + | * tworzenie sygnałów o konkretnej interpretacji fizycznej (częstość sygnału i częstość próbkowania) | ||
| + | * sygnały w pythonie przechowujemy w tablicach numpy | ||
| + | * zapis sygnałów do pliku i wczytywanie sygnałów z plików binarnych | ||
| + | * wczytywanie sygnałów do SVAROGA | ||
| + | |||
| + | [[Analiza_sygnałów_-_ćwiczenia]]/Sygnały | ||
Aktualna wersja na dzień 15:11, 11 gru 2019
Analiza_sygnałów_-_ćwiczenia/Sygnały
Spis treści
Narzędzia wykorzystywane na ćwiczeniach
Python
Python jest językiem programowania wysokiego poziomu, który w połączeniu z bibliotekami NumPy i SciPy do obliczeń naukowych pozwala na szybkie i wygodne programowanie lub analizowanie danych w sposób interaktywny. Przykłady prezentowane w ramach zajęć powinny uruchamiać się zarówno w wersji 2 jak i 3 języka Python, jednak zachęcamy Państwa, aby od początku uczyć się i korzystać z wersji 3 języka.
Szczególnie przydatne na analizie sygnałów będą moduły:
- numpy
- scipy
- matplotlib
Do reprezentowania sygnałów w programach będziemy stosować tablice numpy:
- ndarray
Jest to zarówno efektywne jeśli chodzi o pamięć jak i o szybkość wykonywania operacji matematycznych.
Dokumentacja modułu scipy.signal
Proszę zapoznać się z dokumentacją biblioteki scipy.signal:
https://docs.scipy.org/doc/scipy/reference/
Svarog
Przydatnym narzędziem do analizy sygnałów, z którego będziemy korzystać na zajęciach, jest program SVAROG (pierwotnie skrót od Signal Viewer, Analyzer and Recorder On GPL). Program działa w środowisku Java, jest więc niezależny od systemu operacyjnego (Linux, Windows, OS X…). Svarog pozwala na wczytywanie i analizowanie sygnałów (nie tylko bioelektrycznych), zarówno przy użyciu prostych (FFT, spektrogram) jak i bardziej zaawansowanych (matching pursuit, ICA, DTF itd.) narzędzi. Dzięki współpracy z platformą OpenBCI, możliwa jest rejestracja sygnału (łącznie z metadanymi) bezpośrednio z poziomu graficznego interfejsu użytkownika.
Svarog: uruchamianie i konfiguracja
Aktualną wersję programu Svarog można pobrać [1]. Program nie wymaga instalacji. Po rozpakowaniu paczki do dowolnego katalogu należy uruchomić skrypt „run-svarog.sh” lub uruchomić bezpośrednio plik *.jar.
Aktualnie najnowsza wersja jest tutaj: https://gitlab.com/fuw_software/svarog2-packager/-/releases :)
W przypadku pracy na własnych komputerach, do prawidłowego uruchomienia pluginu do analizy sygnałów, z którego będziemy korzystać w dalszej części ćwiczeń, konieczne jest zainstalowanie środowiska Oracle Java SE w wersji 8, które można pobrać ze strony wydawcy. Alternatywnie, użytkownicy systemu Ubuntu lub pokrewnych dystrybucji mogą zainstalować środowisko Java według instrukcji dostępnych na tej stronie.
Sygnały ciągłe i dyskretne
Próbkowanie w czasie
W tym ćwiczeniu zilustrujemy pojęcia:
- częstość próbkowania
- częstość Nyquista
- aliasing
Zadanie 1: Próbkowanie
W poniższym ćwiczeniu chcemy zbadać efekt próbkowania sygnału w czasie.
- W komputerach nie mamy dostępu do sygnału ciągłego.
- Wartości sygnału znane są tylko w dyskretnych momentach czasu.
- Najczęściej stosujemy równe odstępy czasu [math]dt[/math]
- Odwrotność tych okresów to częstość próbkowania [math]Fs = \frac{1}{dt}[/math]
- Bardzo wygodnie jest myśleć o sygnałach jako o wektorach lub macierzach (rys. na tablicy)
- Do przechowywania sygnałów w pamięci używamy ndarray
Czy próbkując sygnał z częstością [math]Fs = 100[/math][Hz] mogę odwzorować sygnał o dowolnej częstości?
- wytwórz wektor t reprezentujący czas 1s próbkowany z częstością Fs
# -*- coding: utf-8 -*-
import pylab as py
import numpy as np
Fs =100
dt = 1/Fs
t = np.arange(0,1,dt) # czas 'prawie ciągły'
- wytwórz sygnał s, sinus o częstości f =10Hz. Dla przypomnienia wyrażenie: [math] s(t) = \sin(2 \pi f t)[/math] możemy w pythonie zapisać:
s = np.sin(2*np.pi*f*t)
- wykreśl ten sygnał za pomocą punktów i linii
- wykreśl sygnały o częstościach 20, 40, 50, 90 Hz
Efekt aliasingu
Rzućmy okiem na przykład tego efektu: https://youtu.be/SFbINinFsxk
- koła obracają się z pewną częstością zgodnie z kierunkiem ruchu wskazówek zegara;
- na filmie widać, że w pewnych kierunek ten się zmienia, mimo, że samochód wciąż jedzie w tą samą stronę;
- możemy przyjąć umownie, że obrotom zgodnie z kierunkiem wskazówek zegara przypiszemy wartości dodatnie, a obrotom w kierunku przeciwnym wartości ujemne.
- Dlaczego tak się dzieje?
Analogiczne zjawisko przeanalizujemy dla symulowanych sygnałów okresowych. Na nasze potrzeby wygenerujemy sygnały próbkowane z bardzo dużą częstością, które będą dla nas aproksymacją sygnałów ciągłych. Przy ich pomocy zaprezentujemy efekt utożsamiania (aliasingu).
- Proszę wytworzyć wektor reprezentujący czas „prawie” ciągły. Będzie to u nas 1000 wartości z przedziału [0,1) wziętych z odstępem 0,001.
- Teraz proszę wygenerować dwie sinusoidy: jedną o częstości -1 a drugą o częstości 9.
- Proszę wykreślić obie sinusoidy.
- Teraz proszę spróbkować czas i nasze „prawie” ciągłe sinusoidy z okresem próbkowania 0,1. (Trzeba pobrać co 100 element, proszę posłużyć się wycinkami)
- Na tle „prawie” ciągłych sinusoid proszę dorysować punkty ze spróbkowanych sygnałów. Aby punkty były dobrze widoczne proponuję użyć markerów x oraz +.
- Proszę zaobserwować wzajemne położenie punktów.
- Czy można odróżnić sinusoidę o częstości −1 od sinusoidy o częstości 9, jeśli obie są próbkowane z częstością 10?
- Jak można uogólnić tą obserwację?
*
Sygnały testowe
Generowanie sygnałów testowych
Do badania różnych metod analizy sygnałów potrzebne nam będą sygnały o znanych własnościach. W szczególności dobrze jest umnieć nadać sygnałom występującym w postaci cyfrowej, oraz sztucznym sygnałom próbnym pewne własności fizyczne takie jak:
- czętość próbkowania
- czas trwania
- amplituda
Przykład sinus
Sinus o zadanej częstości (w Hz), długości trwania, częstości próbkowania i fazie. Poniższy kod implementuje i testuje funkcję
- [math] \sin(f,T,Fs,\phi) = \sin(2*\pi f t)[/math] dla [math]t \in \{0,T\}[/math]
# -*- coding: utf-8 -*-
import pylab as py
import numpy as np
def sin(f = 1, T = 1, Fs = 128, phi =0 ):
'''sin o zadanej częstości (w Hz), długości, fazie i częstości próbkowania
Domyślnie wytwarzany jest sygnał reprezentujący
1 sekundę sinusa o częstości 1 Hz i zerowej fazie próbkowanego 128 Hz
'''
dt = 1.0/Fs
t = np.arange(0,T,dt)
s = np.sin(2*np.pi*f*t + phi)
return (s,t)
(s,t) = sin(f=10,Fs=1000)
py.plot(t,s)
py.show()
Przykład: eksport sygnału do pliku binarnego
- Przypominamy:
- dtype http://docs.scipy.org/doc/numpy/reference/arrays.dtypes.html#arrays-dtypes-constructing
- open/close
- tofile
- fromfile
- Poniższy kod ilustruje sposób zapisu dwóch funkcji sinus o częstościach 10 Hz i 21 Hz do pliku binarnego:
# -*- coding: utf-8 -*-
import numpy as np
T = 5
Fs = 128
(s1,t) = sin(f=10, T=T, Fs=Fs)
(s2,t) = sin(f=21, T=T, Fs=Fs)
signal = np.zeros((T*Fs, 2), dtype='<f')
signal[:, 0] = s1
signal[:, 1] = s2
# zapis sygnału binarnego:
f_out = open('test_signal1.bin', 'wb') # otwieramy plik do pisania binarnego: 'wb'
signal.tofile(f_out) # zrzucamy zawartość tablicy ''signal'' do pliku identyfikowanego przez ''f_out''
f_out.close() # zamykamy plik
# czynność odwrotna - wczytanie sygnału binarnego
ch = 2 # liczba kanałów
fin = open('test_signal1.bin', 'rb') # otwieramy plik do czytania binarnego: 'rb'
s = np.fromfile(fin, dtype='<f') # tworzymy tablicę sig o typie określonym przez ''dtype''
# wkładając do niej bity z pliku ''fin'' interpretowane zgodnie z ''dtype''
fin.close() # zamykamy plik
s = np.reshape(s,(len(s)/ch,ch)) # zmieniamy tablicę z jednowymiarowej na dwuwymiarową
Przykład: wczytanie sygnału do Svaroga
W celu wczytania zapisanego binarnie sygnału do programu Svarog, po wybraniu File -> Open signal, należy wprowadzić częstość próbkowania sygnału oraz liczbę kanałów.
Zadanie 2: Nieznany typ danych
Posiadamy 3 kanałowy plik binarny z sygnałem EEG. Niestety zapomnieliśmy jaki jest typ zapisanych danych. Proszę wczytać plik i przy pomocy biblioteki matplotlib oraz grafik z fragmentami sygnałów odgadnąć, która z pośród wymienionych zmiennych dtype jest prawdziwa:
- 'float32'
- '>H'
- 'uint64'
- 'float64'
Plik binarny oraz grafiki można pobrać z stąd
Zadanie 3: Nieznana liczba kanałów
Posiadamy n kanałowy plik binarny z sygnałem EKG, EEG i EMG, typ zmiennej to '<f'. Niestety zapomnieliśmy jaka jest liczba kanałów. Proszę wczytać plik i przy pomocy biblioteki matplotlib oraz grafik z fragmentami sygnałów odgadnąć liczbę kanałów. Plik binarny oraz grafiki można pobrać z stąd
Zadanie 4:
Proszę stworzyć nową macierz z n+3 kanałami, zawierającą sygnały z dwóch poprzednich zadań. Następnie proszę zapisać macierz sygnałów do pliku binarnego i otworzyć w programie Svarog.
Delta
Podobnie można zdefiniować funkcję delta o zadanym czasie trwania, częstości próbkowania i momencie wystąpienia impulsu:
- [math] \delta(t_0) = \left\{^{1 \quad t=t_0} _{0 \quad t \ne t_0} \right.[/math]
def delta(t0=0.5, T=1 ,Fs = 128):
dt = 1.0/Fs
t = np.arange(0,T,dt)
d = np.zeros(len(t))
d[np.ceil(t0*Fs)]=1
return (d,t)
Zadanie 5:
Analogicznie do powyższych przykładów proszę zaimplementować i przetestować funkcje generujące:
- funkcję Gabora (funkcja Gaussa modulowana cosinusem) o zadanej częstości i standardowym odchyleniu w czasie, momencie wystąpienia, długości, częstości próbkowania i fazie.
- [math] g = \exp\left(-\frac{1}{2}\left(\frac{t-t_0}{\sigma}\right)^2 \right) \cdot \cos(2 \pi f t + \phi); [/math]
- szum gaussowski o zadanej średniej, odchyleniu standardowym, długości i częstości próbkowania.
Co musimy z tego zapamiętać?
- sygnały dyskretne - dyskretne chwile czasu
- tworzenie sygnałów o konkretnej interpretacji fizycznej (częstość sygnału i częstość próbkowania)
- sygnały w pythonie przechowujemy w tablicach numpy
- zapis sygnałów do pliku i wczytywanie sygnałów z plików binarnych
- wczytywanie sygnałów do SVAROGA
Analiza_sygnałów_-_ćwiczenia/Sygnały