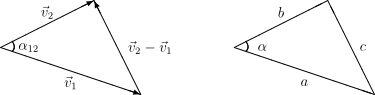Matematyka 1 OO/Dodawanie wektorów i rozkład wektorów: Różnice pomiędzy wersjami
| Linia 104: | Linia 104: | ||
</math> | </math> | ||
| − | [[File: | + | [[File:MO2.png]] |
Przykład | Przykład | ||
| Linia 303: | Linia 303: | ||
<math>|\vec{v}_1|</math>, <math>|\vec{v}_2|</math> i <math>\vec{v}_2\cdot \vec{v}_1</math>. | <math>|\vec{v}_1|</math>, <math>|\vec{v}_2|</math> i <math>\vec{v}_2\cdot \vec{v}_1</math>. | ||
| − | [[File:MO4. | + | [[File:MO4.png]] |
<math>\begin{matrix} | <math>\begin{matrix} | ||
Aktualna wersja na dzień 20:07, 22 maj 2015
Notacja:
Punkty: [math]A=(A_1,A_2)[/math], [math]B=(B_1,B_2)[/math]
Wektory (“różnice punktów”): [math]\overrightarrow{AB}=[B_1-A_1,B_2-A_2][/math]
Zadanie
Znaleźć sumę wektorów [math]\vec{w}_A=[2,3][/math] i [math]\vec{w}_B=[5,-2][/math]
Prosimy studentów o narysowanie układu współrzędnych, zaznaczenie punktów [math]O=(0,0)[/math], [math]A=(2,3)[/math] i [math]B=(5,-2)[/math] i narysowanie wektorów [math]\vec{w}_A[/math] i [math]\vec{w}_B[/math]. Następnie powinni narysować (liniami przerywanymi) dwie proste:
- prostą równoległą do [math]OA[/math] przechodzącą przez punkt [math]B[/math]
oraz
- prostą równoległą do [math]OB[/math] przechodzącą przez punkt [math]A[/math].
Proste te przecinają się w punkcie [math]C[/math] o współrzędnych [math](x_C,y_C)[/math]. Wektor [math]\vec{w}_C=[x_C,y_C][/math] jest szukaną sumą wektorów [math]\vec{w}_A[/math] i [math]\vec{w}_B[/math].
Następnie przeprowadzamy obliczenia opisujące powyższą metodę graficzną.
Znajdujemy równanie prostej [math]OA[/math]:
- [math] y=ax+b: \qquad \left\lbrace \begin{array}{l} 0=a_A\cdot 0 + b_A \\ 3=a_A\cdot 2 + b_A \end{array} \right. \qquad \Rightarrow \qquad \left\lbrace \begin{array}{l} b_A=0 \\ a_A=\frac{3}{2} \end{array} \right. \qquad \Rightarrow \qquad y=\frac{3}{2}x [/math]
Analogicznie znajdujemy równanie prostej [math]OB[/math]: [math]y=-\frac{2}{5}x[/math]
Prosta [math]BC[/math] jest równoległa do [math]OA[/math], więc jej równanie ma postać [math]y=a_Ax+b_{BC}=\frac{3}{2}x+b_{BC}[/math]. Przechodzi ona przez punkt [math]B[/math], więc spełnione musi być równanie [math]y_B=\frac{3}{2}x_{B}+b_{BC}[/math], z którego wyznaczmy [math]b_{BC}[/math]:
- [math] b_{BC}=y_B-\frac{3}{2}x_B=-2-\frac{3}{2}\cdot 5=-2-\frac{15}{2}=-\frac{19}{2} [/math]
Prosta [math]BC[/math] opisana jest równaniem [math]y=\frac{3}{2}x-\frac{19}{2}[/math].
Analogicznie znajdujemy równanie prostej [math]AC[/math]: [math]y=-\frac{5}{2}x+\frac{19}{5}[/math].
Znajdujemy współrzędne punktu [math]C[/math], który jest punktem wspólnym prostych [math]AC[/math] i [math]BC[/math]:
- [math] \left\lbrace \begin{array}{l} y_C=-\frac{2}{5}x_C+\frac{19}{5} \\ y_C=\frac{3}{2}x_C-\frac{19}{2} \end{array} \right. \quad \Rightarrow \quad \frac{3}{2}x_C-\frac{19}{2}=-\frac{2}{5}x_C+\frac{19}{5} \quad \Rightarrow \quad x_C=\frac{133}{19}=7 [/math]
- [math] y_C=\frac{3}{2}x_C-\frac{19}{2}=\frac{21}{2}-\frac{19}{2}=1 [/math]
Punkt [math]C[/math] ma współrzędne [math](7,1)[/math], a więc [math]\vec{w}_C=[7,1][/math].
Ten sam wynik można uzyskać znacznie szybciej licząc
- [math] \vec{w}_C=\vec{w}_A+\vec{w}_B = [2,3]+[5,-2]=[2+5,3-2]=[7,1] [/math]
Metoda bardziej skomplikowana służy temu, żeby pokazać, że graficzne dodawanie wektorów jest równoważne metodzie prostej polegającej na dodawaniu odpowiednich składowych.
Zadanie
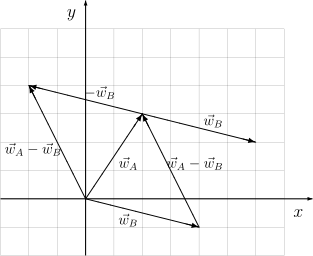
Używając metody graficznej dodawania wektorów, pokazać, że odejmowanie wektora jest równoważne dodawaniu wektora przeciwnego
- [math] \vec{w}_A-\vec{w}_B=\vec{w}_A+(-\vec{w}_B) [/math]
Przykład [math]\vec{w}_A=[2,3][/math], [math]\vec{w}_B=[4,-1][/math]
Zadanie
Rozłożyć wektor [math]\vec{w}=[5,4][/math] w bazie [math]\vec{v}_1=[1,2][/math], [math]\vec{v}_2=[-3,2][/math].
- [math] \vec{w}=a_1\cdot \vec{v}_1 + a_2\cdot \vec{v}_2 [/math]
Porównanie dwóch składowych (często oznaczanych jako składowe [math]x[/math]-owa i [math]y[/math]-owa) powyższego równania wektorowego daje układ równań
- [math] \left\lbrace \begin{array}{l} 5 = a_1\cdot 1 +a_2 \cdot (-3) \\ 4 = a_1\cdot 2 +a_2 \cdot 2 \end{array} \right. [/math]
Mnożąc pierwsze z powyższych równań przez 2 i odejmując drugie równanie otrzymujemy
- [math] 6 = -8a_2 \qquad \Rightarrow \qquad a_2=-\frac{3}{4} [/math]
Podstawienie wyliczonego [math]a_2[/math] do drugiego równania daje
- [math] 4=2a_1-\frac{3}{2} \qquad \Rightarrow \qquad a_1=\frac{11}{4} [/math]
Należy sprawdzić poprawność wyniku licząc odpowiednią kombinację liniową:
- [math] \frac{11}{4}\vec{v}_1 - \frac{3}{4}\vec{v}_2 = \frac{11}{4}[1,2] - \frac{3}{4}[-3,2] = \left[\frac{11}{4}+\frac{9}{4},\frac{11}{2}-\frac{3}{2}\right] = \left[\frac{20}{4},\frac{8}{2}\right] = [5,4] [/math]
Powyższe rachunki trzeba zilustrować rysunkami odpowiadającymi graficznemu dodawaniu wektorów.
Warto poprosić studentów o rozłożenie tego samego wektora [math]\vec{w}[/math]
w dwóch innych “bazach”, np.:
- [math]\vec{u}_1=[-1,3][/math], [math]\vec{u}_2=[2,-6][/math]
- [math]\vec{u}_1=[0,2][/math], [math]\vec{u}_2=[-3,1][/math], [math]\vec{u}_3=[-1,2][/math]
Trzeba wyjaśnić jak brak rozwiązań w przypadku górnym i nieskończenie wiele rozwiązań w przypadku dolnym tłumaczy się na przypadek graficznego dodawania wektorów.
Zadanie
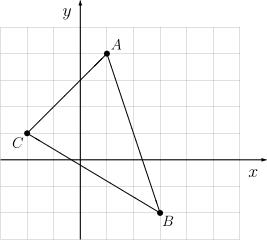
Wierzchołki trójkąta znajdują się w punktach [math]A=(1,4)[/math], [math]B=(3,-2)[/math], [math]C=(-2,1)[/math]. Znaleźć długości boków, kąty miedzy bokami i pole powierzchni tego trójkąta.
Zaczynamy od wyznaczenia wektorów będących “różnicami”
punktów [math]A[/math], [math]B[/math] i [math]C[/math]:
- [math] \overrightarrow{AB}=[2,-6] \qquad \overrightarrow{BC}=[-5,3] \qquad \overrightarrow{CA}=[3,3] [/math]
Długości boków trójkąta są równe długościom tych wektorów
[math]\begin{matrix} &&{\rm d}(A,B)=\sqrt{2^2+6^2}=\sqrt{40}=2\sqrt{10} \\ &&{\rm d}(A,C)=\sqrt{3^2+3^2}=\sqrt{18}=3\sqrt{2} \\ &&{\rm d}(B,C)=\sqrt{5^2+3^2}=\sqrt{34} \end{matrix}[/math]
Następnie wyznaczamy cosinusy kątów między bokami trójkąta
[math]\begin{matrix} \cos (\alpha _A) &&\!\!\!\!\!\!\!\! = \cos \left(\angle \left(\overrightarrow{AB},\overrightarrow{AC}\right)\right) = \frac{\overrightarrow{AB}\cdot \overrightarrow{AC}}{|\overrightarrow{AB}|\cdot |\overrightarrow{AC}|} = \frac{\overrightarrow{AB}\cdot \left(-\overrightarrow{CA}\right)}{|\overrightarrow{AB}|\cdot |\overrightarrow{CA}|} \\ &&\!\!\!\!\!\!\!\! = \frac{2(-3)+(-6)(-3)}{2\sqrt{10}3\sqrt{2}} = \frac{12}{6\sqrt{20}}=\frac{1}{\sqrt{5}} \\[6pt] \cos (\alpha _B) &&\!\!\!\!\!\!\!\! = \cos \left(\angle \left(\overrightarrow{BA},\overrightarrow{BC}\right)\right) = \frac{\overrightarrow{BA}\cdot \overrightarrow{BC}}{|\overrightarrow{BA}|\cdot |\overrightarrow{BC}|} = \frac{(-\overrightarrow{AB})\cdot \overrightarrow{BC}}{|\overrightarrow{AB}|\cdot |\overrightarrow{BC}|} \\ &&\!\!\!\!\!\!\!\! = \frac{(-2)(-5)+(6)(3)}{2\sqrt{10}\sqrt{34}} = \frac{28}{4\sqrt{85}}=\frac{7}{\sqrt{85}} \\[6pt] \cos (\alpha _C) &&\!\!\!\!\!\!\!\! = \cos \left(\angle \left(\overrightarrow{CA},\overrightarrow{CB}\right)\right) = \frac{\overrightarrow{CA}\cdot \overrightarrow{CB}}{|\overrightarrow{CA}|\cdot |\overrightarrow{CB}|} = \frac{\overrightarrow{CA}\cdot (-\overrightarrow{BC})}{|\overrightarrow{CA}|\cdot |\overrightarrow{BC}|} \\ &&\!\!\!\!\!\!\!\! = \frac{(3)(5)+(3)(-3)}{3\sqrt{2}\sqrt{34}} =\frac{1}{\sqrt{17}} \end{matrix}[/math]
Pole powierzchni:
[math]\begin{matrix} S_{ABC} &&\!\!\!\!\!\!\!\! = \frac{1}{2}|\overrightarrow{AB}|\cdot |\overrightarrow{AC}|\sin (\alpha _A) = \frac{1}{2}|\overrightarrow{AB}|\cdot |\overrightarrow{AC}| \sqrt{1-\left(\cos (\alpha _A)\right)^2} \\&&\!\!\!\!\!\!\!\! = \frac{1}{2}\,2\sqrt{10}\,3\,\sqrt{2}\sqrt{1-\frac{1}{5}} = 6\sqrt{5}\sqrt{\frac{4}{5}}=12 \end{matrix}[/math]
Warto zapytać studentów, który z kątów w tym trójkącie jest największy, a który najmniejszy.
- [math] \alpha _A=\arccos \left(\frac{1}{\sqrt{5}}\right) \qquad \alpha _B=\arccos \left(\frac{7}{\sqrt{85}}\right) \qquad \alpha _C=\arccos \left(\frac{1}{\sqrt{17}}\right) [/math]
Trzeba przypomnieć (wyjaśnić), że wszystkie kąty w każdym trójkącie spełniają warunek [math]0\lt \alpha \lt \pi [/math]. W tym przedziale argumentów funkcja cosinus jest ściśle malejąca. Czyli, większa wartość cosinusa odpowiada mniejszej wartości kąta.
- [math] \frac{1}{\sqrt{17}}=\frac{\sqrt{5}}{\sqrt{85}} \lt \frac{1}{\sqrt{5}}=\frac{\sqrt{17}}{\sqrt{85}} \lt \frac{7}{\sqrt{85}} [/math]
- [math] \cos (\alpha _C)\lt \cos (\alpha _A)\lt \cos (\alpha _B) \qquad \Rightarrow \qquad \alpha _C\gt \alpha _A\gt \alpha _B [/math]
Ten wynik należy zilustrować odpowiednim, w miarę dokładnym, rysunkiem.
Zadanie
Udowodnić wzór cosinusów
Mając dwa wektory [math]\vec{v}_1[/math] i [math]\vec{v}_2[/math], chcemy wyrazić długość ich różnicy [math]|\vec{v}_2-\vec{v}_1|[/math] przez [math]|\vec{v}_1|[/math], [math]|\vec{v}_2|[/math] i [math]\vec{v}_2\cdot \vec{v}_1[/math].
[math]\begin{matrix} \left|\vec{v}_2-\vec{v}_1\right|^2 &&\!\!\!\!\!\!\!\!\! = \left(\vec{v}_2-\vec{v}_1\right)\cdot \left(\vec{v}_2-\vec{v}_1\right) = \vec{v}_1\cdot \vec{v}_1+\vec{v}_2\cdot \vec{v}_2-2\,\vec{v}_1\cdot \vec{v}_2 \\ &&\!\!\!\!\!\!\!\!\! = \left|\vec{v}_1\right|^2+\left|\vec{v}_2\right|^2 -2\left|\vec{v}_1\right|\cdot \left|\vec{v}_2\right|\cdot \cos \alpha _{12} \end{matrix}[/math]
- [math] c=\sqrt{a^2+b^2-2ab\cos \alpha } [/math]