Pracownia EEG/EEG wlasnosci EEG spoczynkowego: Różnice pomiędzy wersjami
| Linia 1: | Linia 1: | ||
| − | [[Pracownia EEG|Pracownia EEG] | + | [[Pracownia EEG|Pracownia EEG]] / Własności EEG spoczynkowego: funkcja autokorelacji i widmo |
=Estymacja funkcji autokowariancji, autokorelacji i koherencji sygnału.= | =Estymacja funkcji autokowariancji, autokorelacji i koherencji sygnału.= | ||
Wersja z 06:54, 16 paź 2015
Pracownia EEG / Własności EEG spoczynkowego: funkcja autokorelacji i widmo
Spis treści
Estymacja funkcji autokowariancji, autokorelacji i koherencji sygnału.
Wstęp
Z funkcjami tymi spotkaliśmy się już na zajęciach z analizy sygnałów.
Funkcja autokowariancji sygnału charakteryzuje liniową zależność wartości tego sygnału w danej określonej chwili czasu od wartości (tego samego sygnału) w innej chwili. W przypadku stacjonarnych procesów stochastycznych, przebieg tej funkcji nie zależy od czasu. Oznacza to, że obliczając funkcję autokorelacji sygnału pomiędzy chwilą czasu [math]x(t)[/math] i [math]x(t+\tau )[/math] otrzymamy tę samą wartość, jak dla przypadku obliczania funkcji autokorelacji pomiędzy momentami [math]x(t + T)[/math] i [math]x(t + T+\tau )[/math], gdzie [math]T[/math] to dowolny przedział czasu. Innymi słowy, funkcja autokorelacji procesu stacjonarnego zależy tylko od odstępu czasu pomiędzy próbkami [math]\tau[/math], dla którego jest wyznaczana, a nie od konkretnej chwili czasu. Odrębną klasę sygnałów stanowią procesy niestacjonarne, w przypadku których funkcja autokorelacji będzie zależeć od czasu [math]t[/math] w którym jest obliczana. Estymator funkcji autokowariancji uzyskuje się poprzez obliczanie iloczynów wartości sygnału [math]x[/math] w chwilach czasu [math]t[/math] czyli [math]x(t)[/math] i wartości sygnału [math]x[/math] w chwili czasu t+τ czyli [math]x(t+\tau)[/math] i uśredniając wartości iloczynów po czasie [math]T[/math]:
gdzie:
W przypadku sygnałów ciągłych estymację tę można zapisać w poniższy sposób:
natomiast dla sygnałów dyskretnych jako:
gdzie:
Funkcja autokowariancji może osiągać dowolne wartości, dlatego aby można było porównać przebieg tej funkcji np. pomiędzy dwoma sygnałami, wprowadzono wersję znormalizowaną tej funkcji - funkcję autokorelacji. Normalizacja ta wygląda następująco:
gdzie:
Wariancję sygnału ([math]\gamma (0)=\sigma ^2[/math]) można wyrazić przez funkcję autokowariancji dla przesunięcia [math]\tau =0[/math]. Wynika z tego, że funkcja korelacji przyjmuje wartości z zakresu [math][-1, \, 1][/math]. Ostatecznie estymator funkcji autokorelacji można zapisać jak poniżej:
Funkcję autokorelacji estymuje się w celu określenia, w jakim stopniu wartości sygnału w danej chwili czasu wpływają na wartości sygnału w kolejnych chwilach czasu. Ma to kluczowe znaczenie przy rozpoznawaniu rodzaju procesów fizycznych odpowiedzialnego za generowanie sygnału. Funkcja ta zawsze mam maksimum dla przesunięcia [math]\tau =0[/math].
Cechą charakterystyczną funkcji autokorelacji jest to, iż w przypadku sygnałów harmonicznych, przebieg funkcji ma charakter okresowy, z okresem takim samym jak okres badanego sygnału. W przypadku szumu, funkcja autokorelacji ma kształt funkcji delta Diraca.
Polecenie:
Zaimplementuj funkcję do obliczania funkcji korelacji zgodnie ze wzorem (4). Funkcja powinna przyjmować dwa wektory i maksymalne przesunięcie wzajemne tych wektorów, natomiast zwracać powinna wektor zawierający funkcję autokorelacji. Wywołanie przykładowe:
a = np.array([1,2,3])
print koreluj(a,a,2)
powinno dać wynik:
[-0.5 0. 1. 0. -0.5]
Zadanie 1: Funkcje autokowariancji i autokorelacji
W tym zadaniu posłużymy się sygnałami zarejestrowanymi w punkcie 3. poprzedniego ćwiczenia. Zaobserwuj, na którym kanale rytm alfa osiąga najwyższą wartość. Następnie zaimplementuj w Pythonie następujące kroki:
- Wczytaj dane z wybranego kanału.
- Oblicz funkcję autokorelacji dla sygnału zarejestrowanego w warunkach, gdy osoba badana siedziała z otwartymi oczami. Narysuj autokorelogram, to jest wykres wartości funkcji autokorelacji względem przesunięcia [math]\tau [/math]. Oś [math]\tau [/math] wyskaluj w sekundach.
- Powtórz krok 2, tym razem za sygnału zebranego w warunkach czuwania z zamkniętymi oczami.
- Porównaj autokorelogramy.
Związek autokorelacji z widmem sygnału
Wstęp
Zgodnie z twierdzeniem Chinczyna, z którym zapoznaliśmy się na wykładzie z Analizy Sygnałów, widmową gęstość mocy sygnału można policzyć jako transformatę Fouriera funkcji autokowariancji:
gdzie:
- [math]f[/math] — częstość
- [math]S(f)[/math] — gęstość widmowa mocy
Polecenie
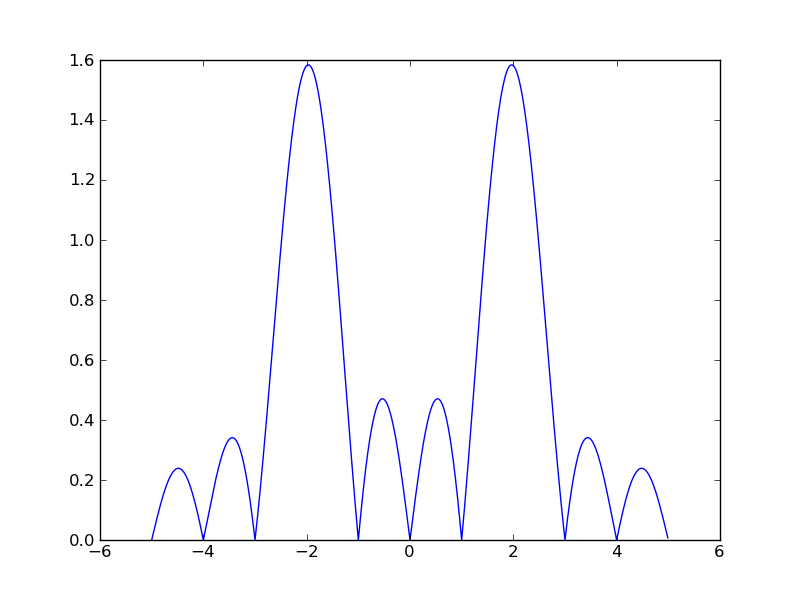
Zaimplementuj funkcję obliczającą transformatę Fouriera dyskretyzując wzór (9) dla zadanego wektora częstości f i zadanej częstości próbkowania sygnału (tutaj 10.0):
Wywołanie przykładowe:
t= np.arange(0,1,0.1)
x = np.sin(2*np.pi*2*t)
f = np.arange(-5,5,1)
X,f = fourier(x,f,10.0)
print X
Powinno dać:
[ 3.15975012e-16 +5.19678720e-16j 1.05325004e-16 +3.51083347e-16j -4.56408351e-16 -2.10650008e-16j 4.91516686e-16 +1.58113883e+00j -1.40433339e-16 -7.02166694e-17j 0.00000000e+00 +0.00000000e+00j -1.40433339e-16 +7.02166694e-17j 4.91516686e-16 -1.58113883e+00j -4.56408351e-16 +2.10650008e-16j 1.05325004e-16 -3.51083347e-16j]
Natomiast wywołanie:
t= np.arange(0,1,0.1)
x = np.sin(2*np.pi*2*t)
f = np.arange(-5,5,0.01)
X = fourier(x,f,10.0)
py.plot(f,np.abs(X))
py.show()
Powinno wytworzyć rysunek:
Zadanie 2: Związek autokorelacji z widmem sygnału
Oblicz gęstość widmową mocy sygnału zarejestrowanego w trakcie czuwania z zamkniętymi oczami, korzystając z twierdzenia Chinczyna oraz metodą Welcha. Znajdź częstość rytmu [math]\alpha[/math] dla osoby, która była badana.