TI/Programowanie dla Fizyków Medycznych/Manipulacja obrazem: Różnice pomiędzy wersjami
| Linia 124: | Linia 124: | ||
===Rozmycie i wyostrzenie=== | ===Rozmycie i wyostrzenie=== | ||
| + | Pierwszym nietrywialnym filtrem jest rozmycie obrazu. Operacja ta jakościowo różni się już od stosowanych poprzednio, gdyż nie opiera się na przekształcaniu wartości w pojedynczym pixelu. W rozmywaniu obrazu nowa wartość przypisywana pixelowi jest różnego rodzaju średnią z wartości pixela i wartości pixeli go otaczających. W najprostszym przypadku może to być po prostu średnia z wartości w danym pixelu i jego ośmiu sąsiadów. Powszechnie jednak stosowanym sposobem rozmywania jest tak zwane rozmycie gaussowskie, gdzie wagi sąsiadujących pixel przy liczeniu średniej liczone są z dwuwymiarowego rozkładu gaussa o zadanej dyspersji. | ||
| + | Chętnym pozostawiam napisanie takiej procedury samodzielnie, natomiast my skorzystamy z gotowej procedury z pakiecie scipy.ndimage. | ||
<source lang="python"> | <source lang="python"> | ||
from scipy import ndimage | from scipy import ndimage | ||
| Linia 129: | Linia 131: | ||
print imag | print imag | ||
</source> | </source> | ||
| − | + | Operacja wyostrzenia powinna być przeciwna do rozmycia. Odtworzenie pierwotnego obrazu na podstawie jego rozmycia niestety nie jest możliwe. Możemy jednak dla dowolnego obrazu policzyć jeszcze większe jego rozmycie, stąd różnice między oryginałem a obrazem rozmytym. Jeżeli taką różnicę pomnożymy razy 1 i dodamy do rozmytego obrazu odtworzymy oryginał. Jeżeli zaś do rozmytego obrazu dodamy tę różnicę pomnożoną przez liczbę większą niż jedne otrzymamy obraz w którym krawędzie będą miały znacznie ostrzejsze brzegi. Zdefiniujmy zatem funkcję wyostrz, która przyjmuje dwa parametry: sigma - czyli dyspersję rozmycia gaussowskiego, oraz a - liczbę przez którą mnożymy różnicę miedzy obrazem rozmytym i oryginałem przez dodaniem jej do obrazu rozmytego. W ten sposób dla parametru a=0 otrzymamy jedynie rozmycie, natomiast dla a>1 wyostrzenie. Przykładowa implementacja poniżej. | |
| − | |||
<source lang="python"> | <source lang="python"> | ||
def wyostrz(tablica, sigma, a): | def wyostrz(tablica, sigma, a): | ||
| Linia 139: | Linia 140: | ||
dodajPasek(wynik,15) | dodajPasek(wynik,15) | ||
return wynik | return wynik | ||
| − | + | </source> | |
| + | Wynik działania dla przykładowych wartości parametru a oraz sigma=4 przedstawione są poniżej | ||
| + | <source lang="python"> | ||
py.imshow(wyostrz(pixel,4,0),cmap=py.cm.gray,interpolation='nearest') | py.imshow(wyostrz(pixel,4,0),cmap=py.cm.gray,interpolation='nearest') | ||
py.show() | py.show() | ||
Wersja z 09:46, 9 cze 2015
Spis treści
Manipulacja obrazem
Ćwiczenia z mainuplacji obrazem rozpocznijmy od wczytania pliku który będziemy przetwarzać. Dla fizyków medycznych naturalnie będzie to plik DICOM.
import dicom
import numpy as np
import pylab as py
plik=dicom.read_file('I00001.dcm')
pixel=plik.pixel_array
print pixel.shape
>>>(2964, 2364)
Stworzona w ten sposób tablica ma dosyć duże rozmiary. O ile wyświetlenie takiego pliku nie jest problemem dla znajdujących się w pracowni komputerów, to bardziej złożona modyfikacja takiej grafiki mogła by z czasem obliczeń znacznie wykraczać poza czas przewidziany na zajęcia. Wyłącznie dla celów dydaktycznych, by ułatwić i przyspieszyć pracę zmniejszymy rozmiar badanego obrazu.
pixel=pixel[::5,::5]
print min(pixel.flatten()),max(pixel.flatten())
>>> 0 3907
Wartości zapisane w tablicy odpowiadającej zmniejszonemu obrazowi mają wartości w przedziale [0,3907]. Metoda wyświetlając imshow najwyższej wartości czyli 3908 przypisze kolor biały, wartości 0 kolor czarny. Aby ułatwić sobie manipulacje kolorami przypiszmy im wartości z zakresu [0,1].
pixel=pixel*1.0/max(pixel.flatten())
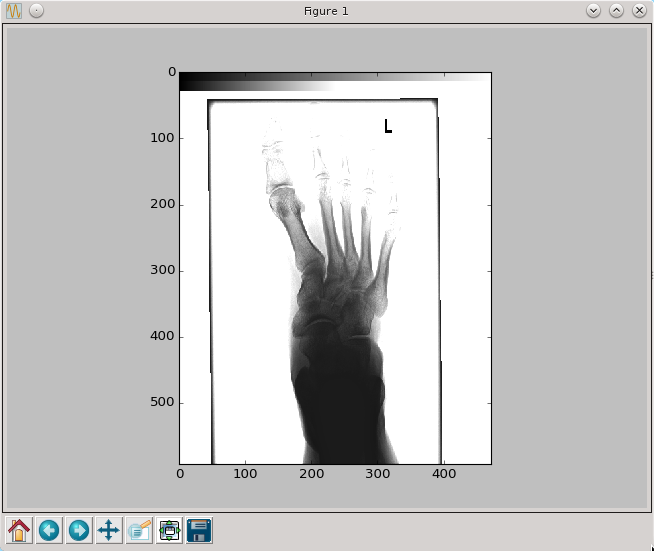
Tak powstały obraz możemy dowolnie modyfikować. Aby lepiej widoczne były skutki manipulacji obrazem dodajmy u góry obrazka þlynne przejście od czerni do bieli
def dodajPasek(tablica, n):
tablica[:n,:]=np.linspace(0,1,tablica.shape[1])
dodajPasek(pixel,30)
py.imshow(pixel,cmap=py.cm.gray,interpolation='nearest')
py.show()
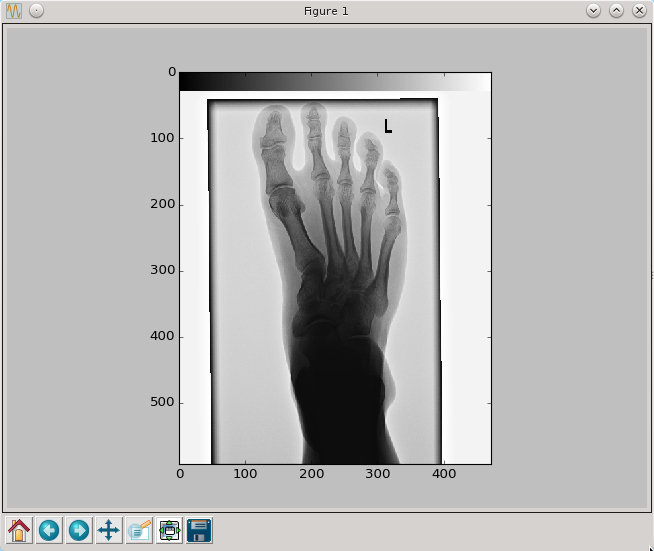 Możemy teraz zdefiniować dowolną funkcję przyjmującą za arguemnty wartości z przedziału [0,1] i zwracającą wartości z tego samego przedziału. Działając taką funkcją na każdy pixel obrazu dokonamy jego transformacji. Najprostrze funkcje jakie mogą przyjść od razu do głowy posiadają już swoje tradycyjne nazwy związane z wpływem jaki mają na obraz.
Możemy teraz zdefiniować dowolną funkcję przyjmującą za arguemnty wartości z przedziału [0,1] i zwracającą wartości z tego samego przedziału. Działając taką funkcją na każdy pixel obrazu dokonamy jego transformacji. Najprostrze funkcje jakie mogą przyjść od razu do głowy posiadają już swoje tradycyjne nazwy związane z wpływem jaki mają na obraz.
Jasność
Najprostszą funkcję od której na Wydziale Fizyki zaczynamy zawsze jest funkcja liniowa. Musimy jedynie zapewnić aby przy wspólczynniku nachylenia większym od 1.0 wynikowe wartości nie przekraczały jedności. Zdefiniujmy zatem jednoparametrową funkcje medyfikującą obraz.
def jasnosc(tablica, a):
def f(x,a):
return min(a*x,1.0)
wynik=tablica.copy()
for x,y in np.ndindex(tablica.shape):
wynik[x,y]=f(tablica[x,y],a)
dodajPasek(wynik,15)
return wynik
Aby móc porównać wynik w pierwotnym obrazem znów wstawiamy pasek szarości ale już o połowę węższy. dzieki temu możemy porównać pasek po operacji przekształcenia i przed nią. Dla a>1 obraz powinien się rozjaśnić, natomiast dla a<1 powinien być ciemniejszy. Zaobaczmy teraz na dwóch przykładach w jaki sposób funkcja jasnosc modyfikuje obraz
py.imshow(jasnosc(pixel,2),cmap=py.cm.gray,interpolation='nearest')
py.show()
py.imshow(jasnosc(pixel,0.5),cmap=py.cm.gray,interpolation='nearest')
py.show()
Gamma
Kolejną narzucającą się funkcją jest podnoszenie wartości zapisanej w tablicy do potęgi. Dla wykładników większych od jeden jasne kolory staną się jeszcze jaśniejsze a przejście między bardzo podobnymi ciemniejszymi odcieniami szarości staną się bardziej widoczne. Dla wykładników mniejszych od jeden, ciemne kolory staną się jeszcze ciemniejsze, natomiast bardzo biskie siebie jasne odcienie staną sie lepiej rozróżnialne. Zdefiniujmy zatem funkcję gamma.
def gamma(tablica, a):
def f(x,a):
return min(x**a,1.0)
wynik=tablica.copy()
for x,y in np.ndindex(tablica.shape):
wynik[x,y]=f(tablica[x,y],a)
dodajPasek(wynik,15)
return wynik
Możemy teraz na dwóch przykładach obejrzeć efekt działania przekształcenia gamma.
py.imshow(gamma(pixel,2),cmap=py.cm.gray,interpolation='nearest')
py.show()
py.imshow(gamma(pixel,0.5),cmap=py.cm.gray,interpolation='nearest')
py.show()
Próg
Czasami isnieje potrzeba przekształcenia obrazu w skali szarości na obraz czarno biały. Na takim czarnobiałym obrazie łatwo w sposób automatyczny dokonywać pomiarów odległości na rysunku. Plik DICOM jest dodatkowo wyposażony w pole opisujące rzeczywiste rozmiary pojedynczego pixela, dzieki czemu taki pomiar w pixelach możemy przełożyć na rzeczywistą odległość. Najporostszym możliwym sposobem przekształcenia obrazu w odcieniach szarości na obraz czarno biały jest ustalenie pewnego progu. Powyżej ustalonej wartości zamieniamy wartości na 1, poniżej na zero. Przykładowa implementacja tej metody przedstawiona jest poniżej.
def prog(tablica, a):
def f(x,a):
return 0 if x<a else 1
wynik=tablica.copy()
for x,y in np.ndindex(tablica.shape):
wynik[x,y]=f(tablica[x,y],a)
dodajPasek(wynik,15)
return wynik
Natomiast jej działanie na obraz wygląda nastepująco
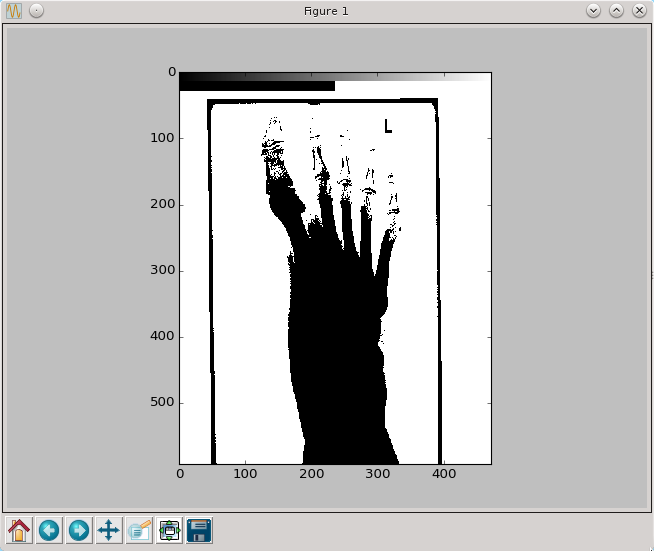
py.imshow(prog(pixel,0.5),cmap=py.cm.gray,interpolation='nearest')
py.show()
Schodek
W bardziej skomplikowanych przypadkach, mogą dla nas być nieistotne zarówno małewartości, opisujące tło obrazu, jak i duże wartości na przykład reprezentujące układ kostny na zdjęciu. Chcialibyśmy skupić się wyłącznie na tkankach miekkich. Wówczas możemy zastosować filtr typu "schodek". Wartościom powyżej pewnego progu, jaki i poniżej pewnegoprogu przypisujemy 0. Wartościom pomiędzy przypisujemy 1. Implementacja poniżej
def schodek(tablica, a,b):
def f(x,a,b):
return 1 if ((x<a) or (x>b)) else 0
wynik=tablica.copy()
for x,y in np.ndindex(tablica.shape):
wynik[x,y]=f(tablica[x,y],a,b)
dodajPasek(wynik,15)
return wynik
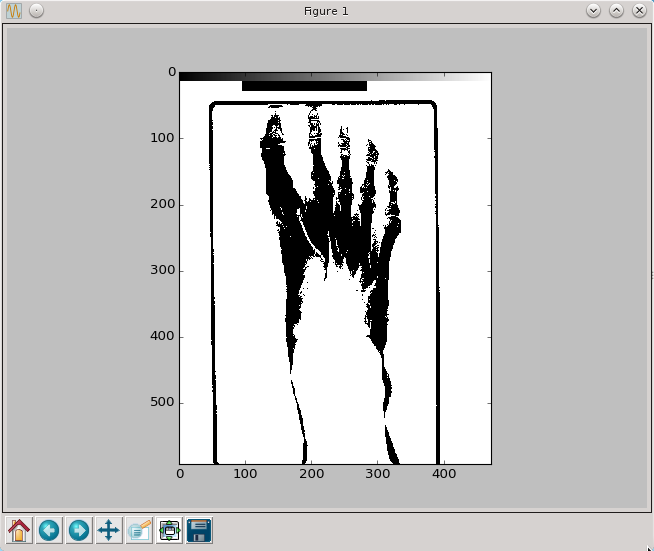
A przyklad działania tutaj.
py.imshow(schodek(pixel,0.2,0.6),cmap=py.cm.gray,interpolation='nearest')
py.show()
Rozmycie i wyostrzenie
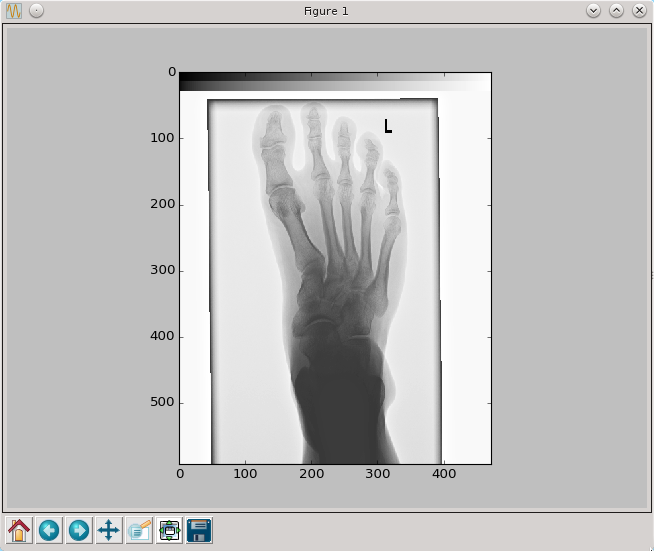
Pierwszym nietrywialnym filtrem jest rozmycie obrazu. Operacja ta jakościowo różni się już od stosowanych poprzednio, gdyż nie opiera się na przekształcaniu wartości w pojedynczym pixelu. W rozmywaniu obrazu nowa wartość przypisywana pixelowi jest różnego rodzaju średnią z wartości pixela i wartości pixeli go otaczających. W najprostszym przypadku może to być po prostu średnia z wartości w danym pixelu i jego ośmiu sąsiadów. Powszechnie jednak stosowanym sposobem rozmywania jest tak zwane rozmycie gaussowskie, gdzie wagi sąsiadujących pixel przy liczeniu średniej liczone są z dwuwymiarowego rozkładu gaussa o zadanej dyspersji. Chętnym pozostawiam napisanie takiej procedury samodzielnie, natomiast my skorzystamy z gotowej procedury z pakiecie scipy.ndimage.
from scipy import ndimage
imag=ndimage.gaussian_filter(pixel,sigma=4)
print imag
Operacja wyostrzenia powinna być przeciwna do rozmycia. Odtworzenie pierwotnego obrazu na podstawie jego rozmycia niestety nie jest możliwe. Możemy jednak dla dowolnego obrazu policzyć jeszcze większe jego rozmycie, stąd różnice między oryginałem a obrazem rozmytym. Jeżeli taką różnicę pomnożymy razy 1 i dodamy do rozmytego obrazu odtworzymy oryginał. Jeżeli zaś do rozmytego obrazu dodamy tę różnicę pomnożoną przez liczbę większą niż jedne otrzymamy obraz w którym krawędzie będą miały znacznie ostrzejsze brzegi. Zdefiniujmy zatem funkcję wyostrz, która przyjmuje dwa parametry: sigma - czyli dyspersję rozmycia gaussowskiego, oraz a - liczbę przez którą mnożymy różnicę miedzy obrazem rozmytym i oryginałem przez dodaniem jej do obrazu rozmytego. W ten sposób dla parametru a=0 otrzymamy jedynie rozmycie, natomiast dla a>1 wyostrzenie. Przykładowa implementacja poniżej.
def wyostrz(tablica, sigma, a):
rozmyty=np.array(ndimage.gaussian_filter(tablica,sigma=sigma))
roznica=tablica-rozmyty
wynik=rozmyty+a*roznica
wynik/=max(wynik.flatten())
dodajPasek(wynik,15)
return wynik
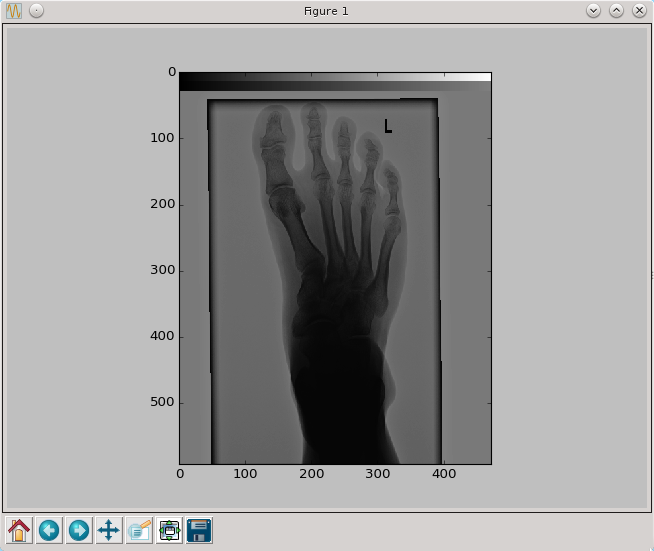
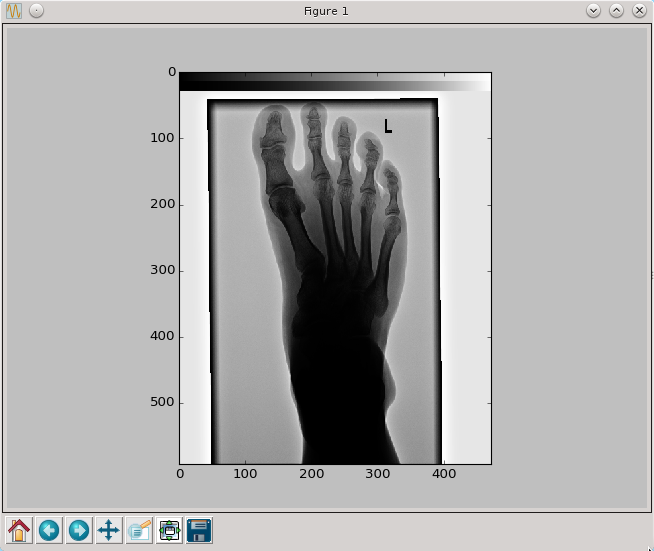
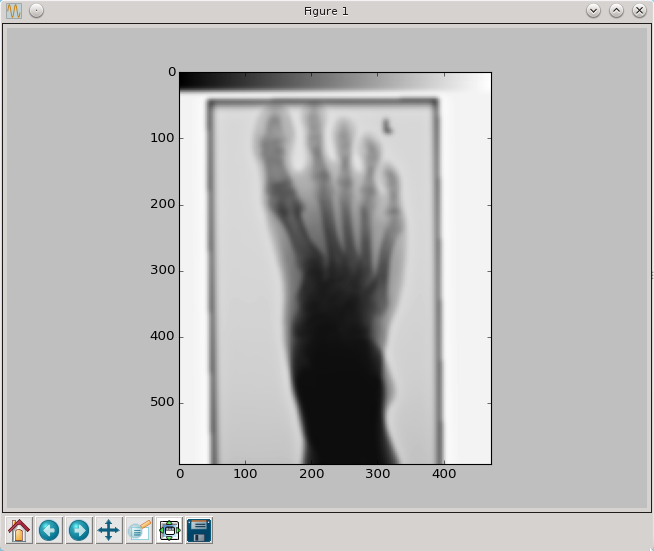
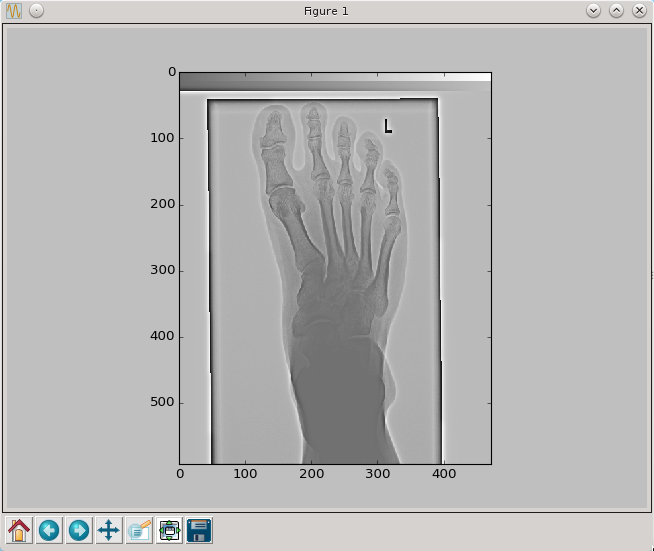
Wynik działania dla przykładowych wartości parametru a oraz sigma=4 przedstawione są poniżej
py.imshow(wyostrz(pixel,4,0),cmap=py.cm.gray,interpolation='nearest')
py.show()
py.imshow(wyostrz(pixel,4,3),cmap=py.cm.gray,interpolation='nearest')
py.show()