Uczenie maszynowe i sztuczne sieci neuronowe/Wykład 2: Różnice pomiędzy wersjami
m |
|||
| Linia 1: | Linia 1: | ||
| − | + | [[Uczenie_maszynowe_i_sztuczne_sieci_neuronowe|powrót]] | |
=Wstęp= | =Wstęp= | ||
==Krótka historia sztucznych sieci neuronowych== | ==Krótka historia sztucznych sieci neuronowych== | ||
Wersja z 16:32, 16 lut 2017
Spis treści
Wstęp
Krótka historia sztucznych sieci neuronowych
- McCulloch i Pitts (1943)[1]
- pierwszy matematyczny opis działania neuronu i przetwarzania przez niego danych. Proste neurony, które mogły modelować funkcje logiczne takie jak OR lub AND; w ich pracach nie ma jeszcze opisu koncepcji uczenia
- Von Neumann
- The computer and the brain (1958): historyczna praca teoretyczna [2]. Wprowadza pomysł uczenia zamiast programowania.
- Perceptron Rosenblatta [3] (1958)
- rozpoznawanie znaków alfanumerycznych, sam perceptron symulowany był na komputerze IBM 704 w Cornell Aeronautical Laboratory. Realizacja sprzętowa: opis:[4] zdjęcie: [5]
- Był wrażliwy na transformacje znaków
- Działał poprawnie (w zakresie swoich możliwości) nawet po uszkodzeniu kilku jednostek
- ADALINE (ADAptive LInear Element)
- stworzony w 1960 przez Widrowa i Hoffa (ze Stanford University). ADALINE był analogowym urządzeniem elektronicznym .
- Okres frustracji i zniechęcenia
- W 1969 Minsky i Papert w swojej książce dowodzili ograniczenia jednowarstwowych sieci neuronowych typu perceptronu i uogólnili je na sieci wielowarstwowe: ”...our intuitive judgment that the extension (to multilayer systems) is sterile”.
Efekt: obcięcie funduszy na badania sieci neuronowych
Lata 70-te były okresem zahamowania funduszy, ale wymyślono w tym czasie kilka ciekawych rozwiązań:
- Anderson i Kohonen niezależnie opracowali koncepcję sieci asocjacyjnych.
- Werbos (1974) po raz pierwszy opracował i użył metody wstecznej propagacji błędu do uczenia sieci neuronowej, ale musiało minąć kilka lat zanim pomysł ten się rozpowszechnił.
- Fukushima (F. Kunihiko) w 1975 zbudował Cognitron a w 1978 rozbudowana wersja — Neocognitron [6] potrafiła rozpoznawać nawet bardzo skomplikowane znaki (pismo chińskie) i była odporna na zniekształcenia, przeskalowania, przesunięcia i obroty znaków.
- ART Steve Grossberg i Gail Carpenter w 1988 wymyślili, w oparciu o analogie biologiczne, sieci ART (Adaptive Resonance Theory)[7].
Od końca lat 80-tych, na skutek nagromadzenia pozytywnych przykładów i rozwoju komputerów pozwalających na symulacje sieci neuronowych, nastąpił gwałtowny rozwój badań nad sieciami neuronowymi.
Ogólne spojrzenie na sieci neuronowe
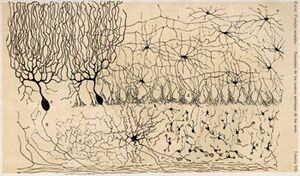
Źródłem inspiracji wspólnym dla większości sztucznych sieci neuronowych jest ludzki mózg.
Mózg składa się z prawie biliona (1012) komórek nerwowych, czyli neuronów (rys. 1) i wspomagających ich pracę komórek glejowych, których jest dziesięciokrotnie więcej. Za funkcje intelektualne odpowiada głównie kora mózgowa. Jej grubość to ok. 3mm 5–6 warstw komórek nerwowych. Każdy neuron może się łączyć, przez wypustki zwane aksonami (rys. 2), nawet z ponad dziesięcioma tysiącami innych neuronów. Miejsce połączenia zakończenia aksonu z ciałem następnego neuronu zwane jest synapsą. Przetwarzanie informacji w neuronie opiera się na sumowaniu potencjałów postsynaptycznych, powstających w odpowiedzi na impulsy dochodzące z zakończeń aksonów innych neuronów. Jeśli wypadkowy potencjał przekroczy próg, generowany jest impuls, który przemieszcza się wzdłuż aksonu jako potencjał czynnościowy. Gdy dotrze do synapsy, pobudza kolejny neuron drogą chemiczną, dzięki neurotransmiterom (wyjątkiem są synapsy elektryczne, występujące częściej niż sądzono pierwotnie). Jeśli suma wygenerowanych w ten sposób potencjałów postsynaptycznych przekroczy próg pobudzenia, generowany jest kolejny potencjał czynnościowy, który przemieszcza się... itd.
Poglądowe animacje:
- Sumowanie i potencjałów postsynaptycznych i przesyłanie informacji przez potencjały czynnościowe: [8]
- Działanie synapsy: [9]
Ogólne cechy sieci neuronowych
- odporność na zniekształcenia bodźców
- odporność na uszkodzenia fragmentów sieci
- zdolność do generalizacji zdobytej wiedzy
- uczenie przykładami zamiast programowania algorytmicznego
- równoległe przetwarzanie danych - szczególnie interesująca własność w przypadku implementacji na maszynach wieloprocesorowych i hardware'owych.
To w jaki sposób modeluje się sieć neuronową zależy w dużej mierze od tego, do jakiego celu ma służyć dany model. Wraz z rozwojem dziedziny modelowania sieci neuronowych wyraźnie zarysował się podział na:
- Biologicznie realistyczne sieci neuronowe — modelowanie i testowanie hipotez dotyczących biologicznych sieci neuronowych. Tym nurtem nie będziemy zajmować się na tych zajęciach.
- Sztuczne sieci neuronowe do zastosowań technicznych i praktycznych. Ten typ sieci będziemy dalej rozważać.
Sieci w technice
W kontekście zastosowań technicznych ogólnie możemy powiedzieć, że:
- Sieć neuronowa, to zbiór połączonych prostych jednostek przetwarzających, których działanie jest luźno inspirowane biologicznymi neuronami.
- Wiedza i możliwości sieci przechowywane są w postaci architektury sieci i siły (wagi) połączeń pomiędzy jednostkami. Wagi ustalane są w procesie zwanym uczeniem.
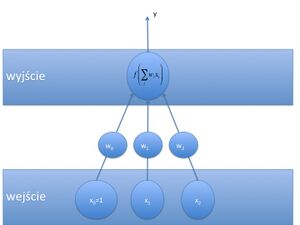
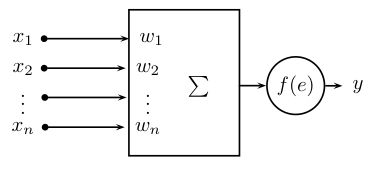 Jednostka przedstawiona na powyższym rysunku wykonuje następujące obliczenia:
[math]y = f \left( \sum_{i=1}^n x_i w_i + w_0 \right) [/math]
Jednostka przedstawiona na powyższym rysunku wykonuje następujące obliczenia:
[math]y = f \left( \sum_{i=1}^n x_i w_i + w_0 \right) [/math]
Kierunki badań i zastosowań sieci neuronowych
- rozpoznawanie kontekstowe i inwariantne obrazów: kompresja, segmentacja, odtwarzanie, ”rozumienie”
- diagnostyka medyczna
- sterowanie i optymalizacja
- sztuczna inteligencja
- ekonomia - szczególnie przydatne zastosowanie, gdy nie ma dobrej teorii.
- predykcja: ocena zdolności kredytowej, prognozy zmian rynku, wspomaganie inwestycji giełdowych
- kwalifikacja i rozpoznawanie podmiotów gospodarczych: np.: czy dane przedsiębiorstwo należy do zwyżkujących, w stanie stagnacji czy też jest w regresji
- kojarzenie i analiza danych — data mining – optymalizacja decyzji gospodarczych
Podstawowe pytania praktyczne
- Jaką wybrać architekturę sieci? Warstwowa “feedforeward”, ze sprzężeniami zwrotnymi, a może każdy z każdym? Ile elementów sieci potrzeba? Jakie powinny być funkcje aktywacji? Aktualizacja synchroniczna czy asynchroniczna, deterministyczna czy losowa?
- Jak nauczyć sieć? Jeśli może nauczyć się na przykładach, to ilu przykładów potrzeba? Ile potrzeba cykli uczenia? Czy przykłady muszą zawierać porządane odpowiedzi (uczenie z nadzorem i bez)? Czy może sieć uczyć się w czasie rzeczywistym, czy uczenie musi być oddzielone od korzystania z sieci?
- Co potrafią zrobić różne typy sieci? Czy potrafią uogólniać — generalizować na podstawie poznanych przykładów?
- Jak zrealizować sieci? Sprzętowo czy symulując na komputerach?
Sieci liniowe
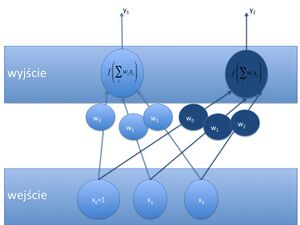
Sieci neuronowe możemy sobie wyobrażać w postaci grafów skierowanych. Ich krawędzie odpowiadają połączeniom między jednostkami i wykonują operację mnożenia przez wagę, zaś w ich wierzchołkach znajdują się jednostki wykonujące pewne działania, np. sumowanie wejść i zastosowanie do tej sumy jakiejś funkcji [math]f[/math]. Koncepcję tą ilustruje poniższy rysunek (rys. 3 i rys. 4):
Pierwszą siecią, którą będziemy omawiać jest sieć złożona z jednostek liniowych. Oznacza to, że funkcja [math]f[/math] występująca w dotychczasowych schematach to funkcja liniowa.
Co może robić sieć liniowa?
Odwzorowania liniowe
W przypadku sieci przedstawionej na rys. 3 wyjście można zapisać jako:
- [math] y = \sum_{i=0}^n w_i x_i[/math]
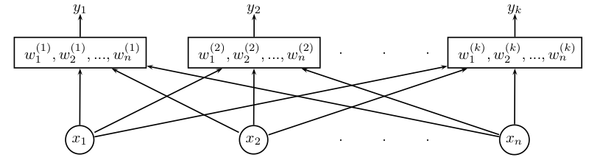
Rozpoznajemy tu znane z poprzedniego wykładu równanie regresji liniowej! A zatem najprostsza sieć liniowa formalnie realizuje regresję liniową. Aby dostrzec co realizuje sieć złożona z wielu elementów liniowych przekształćmy nieco rys. 4 do postaci rys. 5. Wagi związane z jednostką 'm-tą' są grupowane w wektory wag.
Zapiszmy wartości podawane na wierzchołki wejściowe jako wektor kolumnowy:
- [math]\mathbf{x} = (x_1,x_2,\dots,x_n)^T[/math]
Jest on wspólny dla wszystkich jednostek. Wektor wag związanych z 'm-tą' jednostką zapiszmy jako wektor wierszowy:
- [math] \mathbf{w}^{(m)} = (w_1^{(m)}, w_2^{(m)}, \dots,w_n^{(m)})[/math]
z wektorów tych możemy zbudować macierz [math] k \times n [/math]:
- [math] W = \left[ \begin{array}{cccc} w_1^{(1)} & w_2^{(1)} &\dots & w_n^{(1)}\\ w_1^{(2)} & w_2^{(2)} &\dots & w_n^{(2)}\\ \vdots & \vdots & \vdots & \vdots \\ w_1^{(k)} & w_2^{(k)} &\dots & w_n^{(k)} \end{array} \right] [/math]
Jeśli teraz zapiszemy wektor wyjściowy jako wektor kolumnowy: [math]\mathbf{y} = (y^{(1)}, y^{(2)}, \dots y^{(k)})^T[/math] To widać, że:
- [math] \mathbf{y} = W X[/math]
Oznacza to, że warstwa liniowa dokonuje pewnego przekształcenia linowego [math]X \rightarrow Y[/math] z przestrzeni [math]\mathcal{R}^n[/math] do przestrzeni [math]\mathcal{R}^k[/math] zadanego przez macierz [math]W[/math]. Jednym z powszechnych zastosowań jest konstrukcja automatycznie adaptujących się filtrów liniowych.
Obliczenia służące klasyfikacji
Inną możliwością zastosowania sieci liniowej jest możliwość "rozpoznawania" pewnych wzorców wejściowych. Jak to się dzieje?
W tym zastosowaniu musimy zapewnić sobie, że zarówno wektor wejściowy jak i wektor wag są unormowane:
- [math] ||\mathbf{x}||=1[/math]
oraz
- [math] ||\mathbf{w}^{(m)}||=1[/math]
W tej sytuacji wyjście 'm-tej' jednostki jest:
- [math]y^{(m)} = \mathbf{w}^{(m)}\mathbf{x} = \cos \phi[/math]
gdzie [math]\phi[/math] jest kątem między wektorami [math]\mathbf{w}^{(m)}[/math] i [math]\mathbf{x}[/math]. Czyli czym mniejszy kąt między tymi wektorami, tzn. są one do siebie bardziej podobne, tym większy sygnał wyjściowy z neuronu. W tym sensie możemy powiedzieć, że neuron "rozpoznaje" wzorce podobne do zapamiętanych w wagach.
Uczenie sieci liniowej
Celem uczenia sieci jest taka modyfikacja jej wag aby błąd popełniany przez sieć dla przykładów ciągu uczącego [math]\left\{X^{(j)},z^{(j)} \right\}_{j=1,\dots,m}[/math]był możliwie mały.
Przypadek sieci zbudowanej z pojedynczego elementu jest dokładnym odpowiednikiem regresji liniowej. Podobnie jak dla regresji liniowej możemy i tu wprowadzić pojęcie funkcji kosztu zdefiniowanej jako:
- [math]J(w) = \frac{1}{2} \sum_{j =1}^m \left(y^{(j)} - z^{(j)} \right)^2[/math]
tu wartość pożądana dla przykładu [math]j[/math] wynosi [math]z^{(j)}[/math] zaś [math]y^{(j)} [/math] oznacza faktyczna odpowiedź sieci dla tego przykładu.
Analogicznie jak w przypadku regresji liniowej możemy zastosować algorytm spadku gradientowego w wersji stochastycznej lub zbiorczej. W aktualnej notacji wersja zbiorcza algorytmu wygląd tak (dla [math]j[/math]-tej wagi):
- [math]w_{j} := w_j - \alpha \frac{\partial }{\partial w_j } J(w ) = w_j - \alpha \sum _{i=1}^{m} \left( y^{(i)} - z^{(i)} \right) x_j^{(i)} [/math]
zaś w przypadku metody spadku stochastycznego należy wylosować przykład [math]i[/math]-ty z ciągu uczącego i zmodyfikować wagi tak:
- [math]w_{j} := w_j - \alpha \left( y^{(i)} - z^{(i)} \right) x_j^{(i)} [/math]
Przykład funkcji kosztu
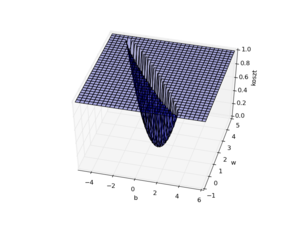
Rozważmy funkcję kosztu dla neuronu o dwóch wejściach i jednym wyjściu. Realizuje on odwzorowanie liniowe [math] y = w x + b[/math]. Niech ciąg uczący będzie {(1,2), (1.5, 3)}. Możemy obliczyć błąd jaki popełnia nasz neuron dla wielu wartości 'w' i dla wielu wartości 'b'. Wykreślając tą wartość we współrzędnych (w,b) otrzymujemy powierzchnię funkcji błędu jak na rys. obok (dla lepszego uwidocznienia kształtu powierzchnia ta został ucięta na poziomie koszt =1).
# -*- coding: utf-8 -*-
from matplotlib.pyplot import plot, show, figure, draw
from mpl_toolkits.mplot3d import axes3d
import numpy as np
def koszt(w,b,CU):
z = np.zeros((len(w),len(b)))
for i,to_w in enumerate( w):
for j,to_b in enumerate( b):
for x, y in CU:
z[j,i] += ( (to_w*x[1] + to_b) - y)**2
return z
# tworzymy ciąg uczący CU
from pybrain.datasets import SupervisedDataSet
CU = SupervisedDataSet(2, 1)
CU.addSample((1, 1), (2,))
CU.addSample((1, 1.5), (3,))
# zakres wag do sprawdzenia
w = np.linspace( -1 ,5, 150)
b = np.linspace(-5, 6, 150)
# obliczmy pow. błędu, czyli wartość błędu dla każdego punktu przestrzeni parametrów.
z = koszt(w,b,CU)
z[np.where(z>1)]=1
fig = figure()
ax = fig.gca(projection='3d')
W,B = np.meshgrid(w,b)
ax.plot_surface(B, W, z, rstride=3, cstride=3, alpha=0.3)
ax.set_xlabel('b')
ax.set_ylabel('w')
ax.set_zlabel('koszt')
ax.set_zlim(0, 1)
show()
Uwagi
Jak wpływa dobór ciągu uczącego na to, czego sieć się nauczyła?
- Funkcja kosztu dla sieci liniowej ma jedno minimum i jest to minimum globalne.
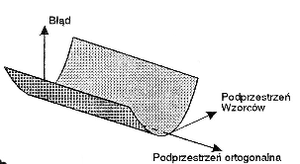
- Jeśli ciąg uczący rozpina przestrzeń możliwych wejść, to sieć dąży do globalnego minimum.
- Jeśli w przestrzeni możliwych wejść istnieje podprzestrzeń ortogonalna do podprzestrzeni wzorców w ciągu uczącym, to sieć dąży do minimum parabolicznej rynny.
Zastanówmy się: Jak szybka jest zbieżność i od czego zależy? Uczenie sieci elementów liniowych
Rozszerzenie metody spadku gradientowego na sieć złożoną z wielu jednostek
Algorytm spadku gradientowego przenosi się w naturalny sposób na sieć elementów liniowych w postaci warstwy:
- w ciągu uczącym [math] \left\{ \left( X^{(j)},Z^{(j)} \right)\right\}_{j=1,\dots,m} [/math]
zamiast wartości z podajemy wektor wartości pożądanych [math]Z[/math]
- zamiast modyfikować wektor wag, modyfikujemy macierz wag [math]W[/math]
- [math]W^{(j+1)} := W^{(j)} - \alpha \left( Y^{(j)}- Z^{(j)} \right) \left(X^{(j)}\right) ^T[/math]
Sieci liniowe MADALINE (Many Adaptive Linear Elements) z tym algorytmem uczenia, są wykorzystywane były jako filtry adaptacyjne np.:
- do tłumienia “echa” w liniach telefonicznych
- do poprawiania stosunku sygnału do szumu, czyli do filtrowania
Przyspieszanie uczenia
- Kontrolowanie wartości parametru [math] \alpha[/math]. Uczenie rozpoczynamy od stosunkowo dużych wartości. Następnie stopniwo zmniejszamy jego wartość.
- Dodanie składnika bezwładności:
- [math] W(k+1) = W(k) - \alpha_1 \left(Y(k) - Z(k)\right)\left( X(k)\right)^T + \alpha_2 M(k)[/math]
gdzie: k - kook uczenia, zaś [math] M(k) =W(k) - W(k-1)[/math] jest poprzednią zmianą wagi.
- [math] \Delta W = - \alpha_1 \left(Y(k) - Z(k)\right)\left( X(k)\right)^T + \alpha_2 M(k)[/math]
Dla prawie płaskiej powierzchni kosztu mamy:
- [math]\Delta W = W(k+1)-W(k) \approx M(k)[/math]
Podstawiając do poprzedniego równania mamy
- [math] \Delta W \approx - \alpha_1 \left(Y(k) - Z(k)\right)\left( X(k)\right)^T + \alpha_2 \Delta W[/math]
Po przekształceniu dostajemy:
- [math]\Delta W \approx - \frac{\alpha_1}{1-\alpha_2} \left(Y(k) - Z(k)\right)\left( X(k)\right)^T [/math]
Oznacza to, że dla prawie płaskiej powierzchni błędu otrzymujemy efektywny współczynnik uczenia [math] \frac{1}{1-\alpha_2}[/math] większy niż w przypadku algorytmu bez bezwładności. Dla typowych wartości [math]\alpha_1 = 0.1[/math] i [math]\alpha_2 = 0.9[/math] otrzymujemy około 10 krotne przyspieszenie!
# -*- coding: utf-8 -*-
from pybrain.structure import FeedForwardNetwork, LinearLayer, FullConnection
from pybrain.supervised.trainers import BackpropTrainer
from matplotlib.pyplot import plot, show, ion, ioff, figure, contour, draw
from mpl_toolkits.mplot3d import axes3d
import matplotlib.animation as animation
import numpy as np
def update_line(num, data, line):
line.set_data(data[...,:num])
return line,
def koszt(w,b,CU):
z = np.zeros((len(w),len(b)))
for i,to_w in enumerate( w):
for j,to_b in enumerate( b):
for x, y in CU:
z[j,i] += ( (to_w*x[1] + to_b) - y)**2
return z
# wytwarzamy pustą sieć
siec = FeedForwardNetwork()
# tworzymy węzły wejściowe i wyjściowe
warstwaWejsciowa = LinearLayer(2)
warstwaWyjsciowa = LinearLayer(1)
# dodajemy węzły do sieci
siec.addInputModule(warstwaWejsciowa)
siec.addOutputModule(warstwaWyjsciowa)
# łączymy węzły
wej_do_wyj = FullConnection(warstwaWejsciowa, warstwaWyjsciowa)
wej_do_wyj.params[0] = -0.1
wej_do_wyj.params[1] = 2.
siec.addConnection(wej_do_wyj)
# inicjujemy sieć
siec.sortModules()
# tworzymy ciąg uczący CU
from pybrain.datasets import SupervisedDataSet
CU = SupervisedDataSet(2, 1)
CU.addSample((1, 1), (2,))
CU.addSample((1, 1.5), (3,))
# zakres wag do sprawdzenia
w = np.linspace( 1.9, 2.1, 50)
b = np.linspace(-0.1, 0.1, 50)
# obliczmy wartości pow. błędu.
z = koszt(w,b,CU)
fig2 = figure(2)
contour(b,w,z,np.linspace(0.0001,0.1,10))
trainer = BackpropTrainer(siec, CU,learningrate=0.08, momentum=0.9)
punkt, = plot(siec.params[0],siec.params[1],'*')
data = np.zeros((2,200))
for i in range(200):
trainer.train()
data[:,i] = siec.params[0], siec.params[1]
line_ani = animation.FuncAnimation(fig2, update_line, 200, fargs=(data, punkt), interval=50, blit=True,repeat=False)
show()
Ograniczenia sieci elementów liniowych
- sieć może jedynie realizować liniowe odwzorowania [math]X \rightarrow Y[/math]
- w odróżnieniu od sieci nieliniowych, liniowe sieci wielowarstwowe nie wnoszą jakościowo nic w stosunku do sieci jednowarstwowych, bo złożenie operacji liniowych da nam i tak operację liniową