Laboratorium EEG/CSP

Laboratorium_EEG/BSS

Ślepa separacja źródeł

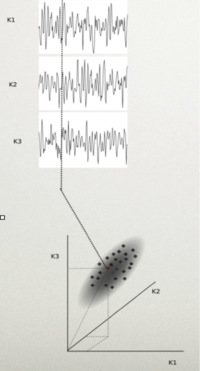
Rozważmy N - kanałowy sygnał EEG. Próbkę tego sygnału możemy przedstawić jako punkt w przestrzeni rozpiętej przez osie, z których każda reprezentuje wartość potencjału w jednym kanale. Cały sygnał tworzy w tej przestrzeni chmurę punktów. Rozciągłość tej chmury w danym kierunku mówi nam o wariancji (zmienności) sygnału w tym kierunku.

Taki zbiór punktów wygodniej jest analizować w układzie współrzędnych zgodnym z osiami głównymi macierzy kowariancji. W dalszej części rozważań założymy, że te przestrzenie, w których rozważamy sygnały są przestrzeniami wektorowymi, a pojedyncze próbki wielokanałowego sygnału są wektorami.

Filtry przestrzenne i ślepa separacja źródeł

Sygnał EEG jest superpozycją aktywności elektrycznej wielu źródeł. Jak można estymować aktywność samych źródeł?

Niech:

[math]s(t)[/math] - aktywność niezależnych źródeł,

[math]x(t)[/math] mierzony sygnał

[math]A[/math] macierz przejścia taka, że:

[math]x(t) = A s(t)[/math] (*)

[math]s(t) = A^{-1}x(t) = P x(t)[/math]

Macierz kowariancji dla sygnałów [math]x(t)[/math] estymujemy tak:

[math] C_x = E[x(t)x(t)^T][/math]

Podstawiając (*) mamy:

[math] C_x = E[x x^T] = E[As(As)^T] = A E[s s^T] A^T = A C_s A^T[/math]

Z założenia, że źródła są niezależne wynika, że macierz [math]C_s[/math] jest diagonalna. Przekształcając powyższe równanie możemy zapisać:

[math]A^{-1} C_x (A^T)^{-1} = P C_x P^T = C_s[/math]

Odwzorowanie [math]P = A^{-1}[/math] diagonalizuje macierz [math]C_x[/math].

Powyższe rozumowanie jest słuszne w przypadku gdy mamy do czynienia z sygnałem stacjonarnym, tzn. jego macierz kowariancji jest niezależna od czasu -> caly czas aktywna jest ta sama konfiguracja źródeł niezależnych. W przypadku gdy tak nie jest to konstrukcję filtra przestrzennego można oprzeć o jednoczesną diagonalizację macierzy kowariancji odpowiadających różnym stanom osoby badanej.

Common Spatial Pattern

Koncepcja

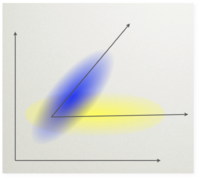
Dla ustalenia uwagi możemy myśleć o eksperymencie wywołującym potencjał P300. Mamy w nim dwie sytuacje eksperymentalne. Oznaczmy (+) próby, w których pojawił się oczekiwany bodziec, zaś (-) gdy pojawił się bodziec standardowy. Chcielibyśmy znaleźć taki montaż, czyli taką kombinację liniową kanałów, które maksymalizuje stosunek mocy (wariancji) sygnałów rejestrowanych w dwóch rożnych warunkach eksperymentalnych.

Formalizm

Metoda ta polega na znalezieniu takiego kierunku w przestrzeni sygnałów, że sygnał któr, które maksymalizuje stosunek wariancji sygnałów rejestrowanych w dwóch rożnych warunkach eksperymentalnych.

Filtry przestrzenne dla SSEP

Teoria

Proszę zapoznać się z koncepcją filtra przestrzennego dla SSVEP zaprezentowaną tu: http://www.eurasip.org/Proceedings/Eusipco/Eusipco2009/contents/papers/1569193209.pdf

Eksperyment ASSR

W eksprymencie wykorzystujemy układ do generacji potencjałów słuchowych stanu ustalonego (ASSR). Wejście układu ASSR typu mini-jack wkładamy w wyjście słuchawkowe w laptopie. Drugie wejście układu ASSR wkładamy do wyjścia triggera we wzmacniaczu. Uruchamiamy plik dźwiękowy MM40tr.wav. Można go znalezc w: http://www.fuw.edu.pl/~suffa/LabEEG/MM40tr.wav

Stymulacja dźwiękowa składa sie z fali nośnej o częstości 400 Hz modulowanej z częstością 40 Hz. Plik dźwiękowy zawiera 5 sekund ciszy i 5 sekund stymulacji, powtórzone 40 razy.

Rejestracja sygnału

1. Zakładamy czepek i elektrody w systemie 10-10, dbamy o to by opory pomiędzy elektrodami były poniżej 5 k G i różnice pomiędzy oporami różnych elektrod nie przekraczały 20%.
2. Oklejamy kwadrat 3x3 elektrod na korze słuchowej z lewej strony (elektrody FT7, FC5, FC3, T7, C5, T3, TP7, CP5, CP3), 3x3 elektrod na korze słuchowej z prawej strony (elektrody FT8, FC6, FC4, T8, C6, T4, TP8, CP6, CP4), elektrody Fz, Cz, Pz i Oz, elektrody referencyjne A1 i A2. W sumie powinno byc 24 elektrody.
3. Elektrodę GND mocujemy na pozycji AFz.
4. Sygnał rejestrujemy z częstością 2048 Hz.
5. Do rejestracji stosujemy scenariusz 'ASSR' w interfejsie obci_gui

Analiza

JZ: zmieniłbym analizę na czas-częstość i zrobił porównanie montażu usznego do filtra G.G. Moliny

Początek stymulacji dźwiękowej oznaczymy jako 0. Poniższą analizę zastosuj dla sygnałów w referencji do uśrednionych odprowadzeń usznych A1 i A2. Wyznaczenie pasma częstości odpowiedzi ASSR

1. Z sygnału wycinamy fragmenty od 0 do 5 sek. dla wszystkich elektrod położone nad korą słuchową.
2. Dla każdej realizacji obliczamy widma metodą Welcha.
3. Otrzymane zespolone widma uśredniamy po realizacjach.
4. Sprawdzamy czy w uśrednionym widmie występuję maksimum w częstości modulacji tj. 40 Hz.

Wyznaczenie przebiegu czasowego ERD i ERS

1. Zaprojektuj filtry pasmowo przepustowe (Chebyszewa 2 rodzaju) zgodne z wyznaczonym pasmem. Zbadaj funkcje przenoszenia i odpowiedzi impulsowej.
2. Powycinaj sygnały od -5 do +10 sekund (wszystkie kanały). Przefiltruj każdą realizację.
3. Oblicz moc chwilową za pomocą transformaty Hilberta (kwadrat modułu transformaty Hilberta).
4. Uśrednij moc chwilową po realizacjach.
5. Oblicz względną zmianę mocy chwilowej względem czasu -4 do -2. W ten sposób otrzymasz przebieg ERD i ERS w czasie.
6. Wykreśl ERD i ERS w układzie topograficznym. (Rozmieść subploty tak, aby z w przybliżeniu odpowiadały pozycjom elektrod).

Transformacja Hjortha

Transformacja Hjortha jest przybliżeniem numerycznym transformacji Laplace'a, czyli drugiej pochodnej przestrzennej. Obliczamy ją jako różnicę potencjału pomiędzy daną elektrodą i średnią z czterech sąsiednich elektrod. Przelicz potencjały z elektrod, w których występuję odpowiedź ASSR na montaż Hjortha i powtórz analizę ERD/ERS opisaną powyżej.