Ćwiczenia 6
Analiza_sygnałów_-_ćwiczenia/Filtry
Spis treści
Wprowadzenie
- W analizie sygnałów filtowanie rozumiane jest najczęściej jako operacja mająca na celu usunięcie z sygnału pewnych składowych. Często operacja ta dotyczy składowych charakteryzowanych przez częstości np.:
- w sygnale EEG wiemy, że znaczącym artefaktem jest sygnał pochodzący od sieci energetycznej, zatem stosujemy filtr usuwający składową około 50Hz (w Europie).
- inny przykład z tej samej dziedziny: interesuje nas czynność alfa (8 -12 Hz), chcemy zatem usunąć z sygnału składowe o niższych i o wyższych częstościach.
- Filtry często są realizowane w postaci systemów LTI (linear time invariant):
- dla takich systemów funkcjami własnymi są zespolone eksponensy (czyli na mocy wzorów Eulera: sinusy i cosinusy)
- w przestrzeni częstości filtrowanie odpowiada przemnożeniu każdej składowej częstościowej przez pewną liczbę (zespoloną)-> zatem zmienić się może amplituda i faza każdej częstości
- w dziedzinie czasu to mnożenie odpowiada splotowi sygnału z pewną funkcją tzw.funkcją odpowiedzi impulsowej
Filtry cyfrowe
Działanie filtra w dziedzinie czasu
Najczęściej, wyjście filtra jest kombinacją liniową:
- [math] y[n] = b(1)x[n] &+ b(2)x[n-1] + ... + b(n_b+1)x[n-n_b][/math]
- [math] - a(2)y[n-1] - ... - a(n_a+1)y[n-n_a] [/math]
gdzie:
- [math] n_b [/math] liczba przeszłych próbek wejściowych [math] x [/math]
- [math] n_a [/math] liczba przeszłych próbek wyjściowych [math] y [/math]
użytych do obliczenia aktualnego wyjścia [math] y[n] [/math].
Większa z liczb [math] n_b [/math] i [math] n_a [/math] określa rząd filtra.
Zauważmy, że matematycznie operacje te odpowiadają splataniiu próbek wejściowych z wektorem [math]b[/math] i próbek wyjściowych z wektorem [math]a[/math].
Nazewnictwo
- Jeśli [math]n_a=0 [/math] i [math]n_b \ne 0 [/math] filtr nazywany jest filtrem o skończonej odpowiedzi impulsowej (FIR), czasem jest on nazywany średnią ruchomą (MA).
- Jeśli [math]n_b=0 [/math] i [math]n_a \ne 0 [/math] filtr ma nieskończoną odpowiedź impulsową (IIR). Bywa też nazywany filtrem autoregresyjnym (AR).
- Jeśli [math]n_b \ne 0 [/math] i [math]n_a \ne 0 [/math] także jest filtrem o nieskończonej odpowiedzi impulsowej. Czasem mówi się o nim filtr ARMA - autoregressive moving average.
Zwykle filtry IIR mają niższy rząd niż filtry FIR o tym samym poziomie tłumienia.
Przejście do dziedziny częstości
- [math] y[n]+ a(2)y[n-1] + ... + a(n_a+1)y[n-n_a] = [/math]
- [math] =b(1)x[n] + b(2)x[n-1] + ... + b(n_b+1)x[n-n_b] [/math]
- [math] y[n]+ a(2)y[n-1] + ... + a(n_a+1)y[n-n_a] = [/math]
zastosowanie transformaty Z do bu stron daje:
- [math]A(z)Y(z)=B(z)X(z)[/math]
Przekształcamy:
- [math]Y(z)=A(z)^{-1}B(z)X(z) =H(z)X(z)[/math]
Funkcja[math]H$[/math] w tym równaniu nazywana jest funkcją przenoszenia filtra. Ma ona formę ilorazu dwóch wielomianów:
- [math]H(z)=\frac{b(1)+b(2)z^{-1}+\dots+b(n_b+1)z^{-n_b}}{a(1)+a(2)z^{-1}+\dots+a(n_a+1)z^{-n_a}}[/math]
Działanie filtra w dziedzinie częstości
- Funkcję przenoszenia zależną od częstości, [math]H(f)[/math], można uzyskać podstawiając [math] z=e^{i 2 \pi f}[/math]
- Ta funkcja przypisuje każdej częstości [math]f[/math] pewną liczbę zespoloną, która ma moduł [math]M[/math] i fazę[math]\phi[/math]:
- [math]H(f)=M(f)e^{i \phi(f)}[/math]
- Zatem działanie filtra to mnożenie każdej składowej Fourierowskiej sygnału przez liczbę zespoloną [math]H(f)[/math];
- Widać więc, że filtr może takiej składowej zmienić amplitudę i fazę, ale nie może jej zmienić częstości.
- Jest to przejaw tego, że sinusoidy są funkcjami własnymi układów LTI
Opóźnienie grupowe
Pokazaliśmy, że filtr mnoży każdą składową przez liczbę [math]M(f)e^{i \phi(f)}[/math], przez co zmienia jej fazę o [math]\phi(f)[/math]. W konsekwencji składowa o częstości [math]f[/math] pojawia się na wyjściu filtra z opóźnieniem: [math]\tau_g(f)=-\frac{d \phi(f)}{d f}[/math]
- Jeśli zależność fazy od częstości jest liniowa (tak jest dla filtrów FIR) to [math]\tau_g(f)=const[/math], czyli wszystkie składowe pojawiają się z tym samym opóźnieniem.
- Dla nieliniowej zależności [math]\phi(f)[/math] każda składowa jest opóźniona inaczej. Powoduje to dodatkowe zniekształcenia sygnału.
Interpretacja własności fazowych filtru łatwiejsza jest jeśli zamiast fazy wykreślimy opóźnienie fazowe lub grupowe.
- Opóźnienie fazowe zdefiniowane jest jako:
- [math]\tau_p(\omega )=-\frac{\phi(\omega)}{\omega}[/math]
Sens tej definicji widać jeśli zastosujemy ją do sinusa o częstości [math]\omega_1[/math] i fazie [math]\phi_1[/math]. [math]\sin(\omega_1 t + \phi_1)= \sin(\omega_1 t - \omega_1 \tau_p(\omega_1)) = \sin(\omega_1 (t-\tau_p(\omega_1))) [/math]
- opóźnienie grupowe zdefiniowane jest jako:
- [math]\tau _g(\omega )=-\frac{d \phi (\omega )}{d \omega }[/math]
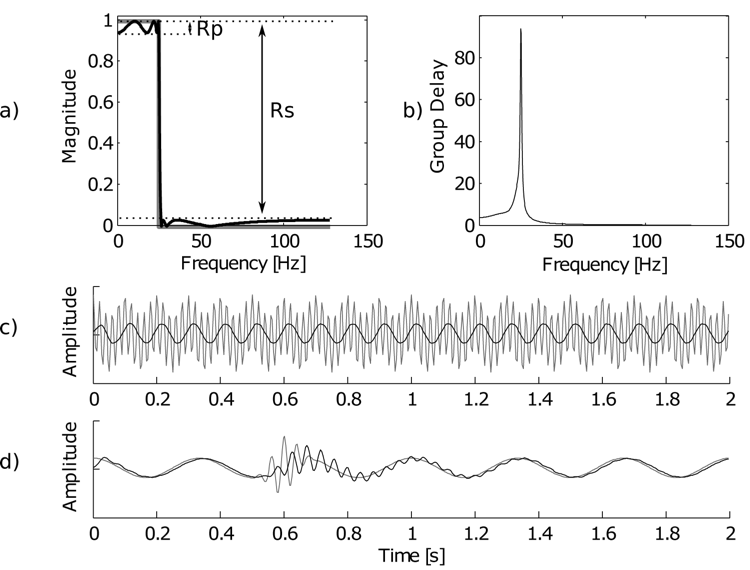
Sens tej definicji widać jeśli rozważymy co stanie się z sygnałem składającym się z dwóch cosinusiod o bliskich sobie częstościach [math]\omega_1[/math] i [math] \omega_2[/math]. Załóżmy, że filtr przenosi każdą z nich z niezmienioną amplitudą i jedynie faza ulega przesunięciu odpowiednio o [math]\phi_1[/math] i [math]\phi_2[/math]. Na wejściu nasz sygnał można przedstawić tak:
- [math]\cos(\omega_1 t) + \cos(\omega_2 t) = 2\cos\left(\frac{\omega_1-\omega_2}{2}t\right)\cos\left(\frac{\omega_1+\omega_2}{2}t\right)= 2\cos\left(\frac{\Delta\omega}{2}t\right)\cos\left(\frac{\omega_1+\omega_2}{2}t\right)[/math]
Widać, że takie dwa cosinusy powodują efekt dudnienia. Innymi słowy można je postrzegać jako oscylację z częstością średnią obu cosinusów modulowaną wolno zmienną ([math]\Delta \omega/2[/math]) obwiednią. Sygnał wyjściowy z naszego filtru modyfikującego tylko fazy można zapisać tak:
- [math]y = \cos(\omega_1 t +\phi_1) + \cos(\omega_2 t +\phi_2) = 2\cos\left(\frac{\omega_1-\omega_2}{2}t +\frac{\phi_1-\phi_2}{2}\right)\cos\left(\frac{\omega_1+\omega_2}{2}t+\frac{\phi_1+\phi_2}{2}\right)[/math]
Oznaczmy [math]\Delta \phi = \phi_1 - \phi_2[/math].
- [math] y = 2\cos\left(\frac{1}{2} \left(\Delta\omega t +\Delta\phi \right) \right)\cos\left(\frac{\omega_1+\omega_2}{2}t+\frac{\phi_1+\phi_2}{2}\right) [/math]
Wprowadzając [math] t_g = - \frac{ \Delta \phi}{\Delta \omega}[/math] mamy:
- [math] y = 2\cos\left(\frac{1}{2} \left(\Delta\omega t - \Delta\omega t_g \right) \right)\cos\left(\frac{\omega_1+\omega_2}{2}t+\frac{\phi_1+\phi_2}{2}\right) = [/math]
- [math] = 2\cos\left(\frac{1}{2} \Delta\omega \left(t - t_g \right) \right)\cos\left(\frac{\omega_1+\omega_2}{2}t+\frac{\phi_1+\phi_2}{2}\right) [/math]
Zatem widzimy, że obwiednia przesunięta jest w czasie o [math]t_g[/math]. W granicznym przypadku ciągłym [math]\lim_{\Delta \omega \to 0}t_g = \tau_g[/math]
Filtrowanie z zerowym przesunięciem fazowym
Można temu zaradzić następującą procedurą:
- filtrujemy sygnał [math]x[0], \dots , x[n] \rightarrow y[0],\dots, y[n][/math] wprowadzamy przesunięcie fazy o [math]\phi(f)[/math]
- odwracamy kolejność próbek i ponownie filtrujemy [math] y[n],\dots,y[0] \rightarrow y'[n],\dots,y'[0] [/math] wprowadzamy przesunięcie fazy o [math]-\phi(f)[/math]
- odwracamy kolejność próbek: [math]y'[0],\dots,y'[n] [/math]
Efektywnie wygląda to tak jakbyśmy przefiltrowali sygnał filtrem o funkcji przenoszenia z zerowym przesunięciem fazowym: [math]H_{eff}(f)=A(f)e^{i \phi(f)}\cdot A(f)e^{-i \phi(f)}= A(f)^2[/math]
Pytanie
- co to jest odpowiedź impulsowa filtra?
- jak filtr działa w dziedzinie czasu?
- co to jest funkcja przenoszenia filtra?
- jak filtr działa w dziedzinie częstości?
Klasyczne filtry IIR
Mamy cztery klasyczne typy filtrów IIR:
- Butterwortha
- daje monotoniczną funkcję przenoszenia
- Czebyszewa typu I
- - dopuszczalne tętnienia w paśmie przenoszenia, monotoniczne w paśmie zaporowym
- Czebyszewa typu II
- -monotoniczne w paśmie przenoszenia, dopuszczalne tętnienia w paśmie zaporowym, nieco mniej strome zbocze opadające funkcji przenoszenia niż dla typu I
- Filtr eliptyczny
- mają dopuszczalne tętnienia zarówno w paśmie przenoszenia jak i tłumienia. Dają najbardziej strome zbocza przy tym samym rzędzie co powyższe wersje.
Specyfikacja filtra
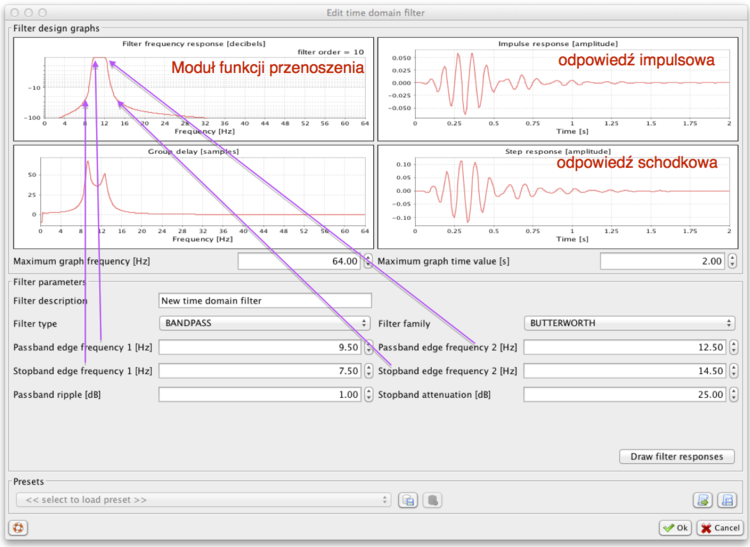
Projektowanie filtra w programie SVAROG
Program SVAROG ma wygodne narzędzie do projektowania filtrów IIR. Zanim przejdziemy do implementowania tych filtrów w pythonie, spróbujemy nabrać wyczucia w SVAROGU.
Przydadzą nam się pliki: Plik z sygnałem EKG Plik z metadanymi do tego sygnału
Implementacja filtrowania: funkcja lfilter
Filtrowanie zgodne z powyższymi równaniami zaimplementowane jest w pythonie w module scipy.signal jako funkcja lfilter.
Podstawowe wywołanie tej funkcji dla sygnału we wygląda następująco: wy = scipy.signal.lfilter(b,a,we) gdzie b, a są to współczynniki z poprzedniego równania. np:
import numpy as np
import pylab as py
from scipy.signal import lfilter
b = np.array([0.7, 0.5]) # licznik
a = np.array([1.0, -0.9]) # mianownik
we = np.random.randn(100)
wy=lfilter(b,a,we);
py.subplot(2,1,1)
py.plot(we)
py.subplot(2,1,2)
py.plot(wy)
py.show()
Projektowanie filtru
Specyfikacja własności filtru
Filtr specyfikujemy opisując moduł jego pożądanej funkcji przenoszenia:
- ogólne określenie granic pasma przenoszenia np: dla sygnału próbkowanego 128 Hz zaprojektować filtr dolnoprzepustowy 30 Hz, oznacza, że w idealnej sytuacji filtr będzie przenosił bez zmian częstości od 0 do 30 Hz a od 30Hz do 64Hz będzie całkowicie tłumił.
- w bardziej rygorystycznym opisie możemy dodatkowo podać:
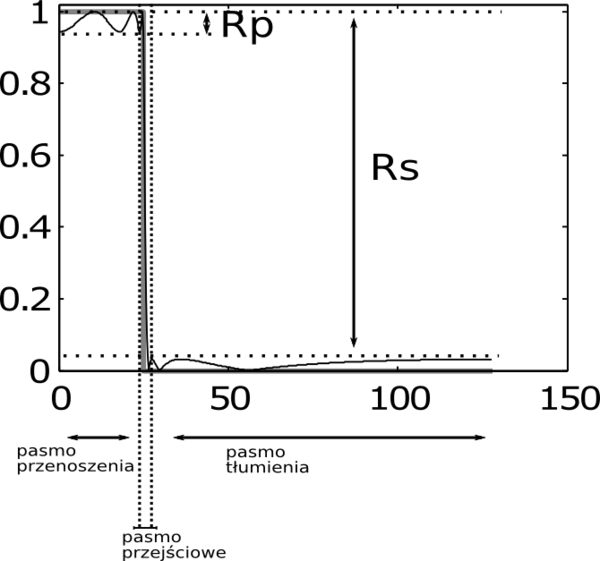
- dopuszczalną amplitudę oscylacji Rp w paśmie przenoszenia (pass band),
- minimalne tłumienie Rs pasma tłumienia (stop band),
- szerokość pasma przejściowego
Oznaczenia jak na poniższym rysunku.
W określaniu parametrów filtrów używa się często pojęcia decybel [dB]. Dwa poziomy sygnału [math]P[/math] oraz [math]P_0[/math] różnią się o [math]n[/math] decybeli, jeżeli
- [math]n = 10 \log _{10} \frac{P}{P_0} = 10 \log_{10}\left(\frac{A}{A_0}\right)^2 = 20\log_{10}\frac{A}{A_0} [/math]
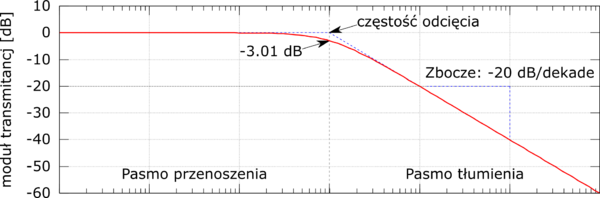
- można też podać częstość odcięcia i zbocze filtru zgodnie z oznaczeniami na poniższym rysunku:
Funkcje do projektownaia filtrów FIR
W module scipy.signal mamy kilka funkcji do projektowania filtrów typu FIR.
firwin
Najprostszą koncepcyjnie metodą projektowania filtrów FIR jest metoda okienkowa. Metoda składa się z następujących kroków: w dziedzinie częstości projektowana jest idealna funkcja przenoszenia, obliczana jest od niej odwrotna transformata Fouriera, następnie otrzymana sekwencja czasowa (odpowiedź impulsowa) jest przemnażana przez wybrane okno.
Metoda ta zaimplementowana jest w funkcji scipy.signal.firwin(numtaps, cutoff, width=None, window='hamming', pass_zero=True, scale=True, nyq=1.0). Pozwala ona projektować filtry dolno- i górno- przepustowe oraz pasmowo przepustowe i pasmowo zaporowe metodą okienkową.
Najważniejsze parametry (kompletny opis w dokumentacji firwin):
- numtaps: int, ilość współczynników filtru (rząd filtru+1). Liczba ta musi być parzysta jeśli pasmo przenoszenia ma zawierać częstość Nyquista.
- cutoff: częstość odcięcia filtru. Może być jedną liczbą zmiennoprzecinkową dla filtru dolno- lub górno- przepustowego lub tablicą dla filtrów pasmowych. Wyrażamy ją w tych samych jednostkach co nyq i musi zawierać się pomiędzy 0 a nyq.
- window: napis lub krotka: określa jakiego okna użyć do projektu filtru. Może to być dowolne okno spośród opisanych w scipy.signal.get_window
- pass_zero: bool, Jeśli True to zero jest przenoszone, jeśli False to nie jest. Ten parametr decyduje jak jest interpretowane pierwsze pasmo od 0 do cutoff - czy ma to być pasmo przenoszone czy tłumione.
- nyq: float. Częstość Nyquista.
- Zwraca: współczynniki b
Przykładowe projekty
We wszystkich poniższych przykładach zakładamy, że częstość próbkowania wynosi 256Hz:
- filtr dolnoprzepustowy rzędu 20 z częstością odcięcia 40Hz:
firwin(21, 40/128.0, nyq= 1) firwin(21, 40, nyq= 128)
- filtr górnoprzepustowy rzędu 15 z częstością odcięcia 5 Hz:
firwin(16, 5, nyq= 128, pass_zero=False)
- pasmowo przepustowy 5 rzędu przenoszący częstości pomiędzy 8 a 14 Hz:
firwin(6, [8 14], nyq= 128, pass_zero=False)
- pasmowo zaporowy 5 rzędu tłumiący częstości pomiędzy 8 a 14 Hz:
firwin(6, [8 14], nyq= 128, pass_zero=True)
Demo własności "audio" filtrów tego typu: applet
firwin2
Funkcja scipy.signal.firwin2(numtaps, freq, gain, nfreqs=None, window='hamming', nyq=1.0) również implementuje okienkową metodę projektowania filtrów FIR. Daje ona nieco większą swobodę w kształtowaniu idealnej funkcji przenoszenia. Zadaje się ją przez podanie dwóch wektorów: freq i gain. Wektor freq definiuje punkty w częstości (jednostki takie same jak nyq, muszą zawierać 0 i nyq) dla których znana jest wartość pożądanego przenoszenia. Pożądane wartości przenoszenia odpowiadające kolejnym częstościom definiowane są w gain. Wartości freq muszą być ułożone w kolejności rosnącej, dopuszczalne jest powtórzenie tej samej wartości częstości i odpowiadających im różnych wartości gain aby zdefiniować nieciągłość funkcji przenoszenia. Znaczenie pozostałych parametrów jest takie samo jak dla firwin.
funkcja dostepna jest począwszy od wersji scipy 0.9.0
Przykład: filtr górno przepustowy. Liniowo narastające przenoszenie pomiędzy 20 a 40 Hz:
f = np.array([0, 20, 40, 128])
g = np.array([0, 0, 1, 1])
b = firwin2(50,f,g,nfreqs, nyq=128)# licznik
Badanie własności filtru w dziedzinie częstości
Podstawowe własności filtru możemy łatwo odczytać z wykresu przedstawiającego moduł funkcji przenoszenia i jej fazę w zależności od częstości. Moduł funkcji przenoszenia najczęściej wykreśla się w skali pół logarytmicznej.
W module scipy.signal zaimplementowana jest funkcja freqz, która wylicza wartości funkcję przenoszenia filtru zadanego współczynnikami b, a w zadanej ilości dyskretnych częstości. Jej użycie ilustruje poniższy przykład:
Przykład
Poniższy przykład przedstawia własności filtra dolnoprzepustowego rzędu 50 o częstości odcięcia równej połowie częstości Nyquista.
W dziedzinie częstości
import numpy as np
import pylab as py
from scipy.signal import freqz, firwin
b = firwin(50,0.5)# licznik
a = np.array([1.0]) # mianownik
n = 1000 # n ilość punktów na których będzie obliczona funkcja h
w, h = freqz(b,a,n)
m = np.abs(h) # moduł transmitancji
phi = np.unwrap(np.angle(h)) # faza
py.subplot(4,1,1)
py.plot(w,20*np.log10(m))
py.ylabel('[dB]')
py.title('moduł transmitancji')
py.subplot(4,1,2)
py.plot(w,phi)
py.title('faza transmitancji')
py.ylabel('rad')
py.xlabel('rad/próbki')
fazowe = - phi/w
py.subplot(4,1,3)
py.plot(w,fazowe)
py.ylim([20,30])
py.title('opóźnienie fazowe')
py.ylabel('próbki')
py.xlabel('rad')
grupowe = - np.diff(phi)/np.diff(w)
py.subplot(4,1,4)
py.plot(w[:-1],grupowe)
py.ylim([20,30])
py.title('opóźnienie grupowe')
py.ylabel('próbki')
py.xlabel('rad')
py.show()
W dziedzinie czasu
Porównajmy działanie tego filtra w czasie z funkcjami przesunięć fazowych i grupowych:
import numpy as np
import pylab as py
from scipy.signal import lfilter, firwin
b = firwin(50,0.5)# licznik
py.subplot(3,1,1)
py.plot(b,'o')
s1 = np.zeros(100)
t = np.arange(0,1,0.01)
s2 = np.sin(2*np.pi*10*t)
s = np.concatenate((s1,s2))
py.subplot(3,1,2)
py.plot(s)
py.subplot(3,1,3)
y = lfilter(b,1,s)
py.plot(y)
py.show()
Zadania
- Zaprojektuj i zbadaj własności filtru:
- FIR dolno z pasmem przenoszenia od 30 Hz dla sygnału próbkowanego 256 Hz
- Znajdź rząd filtru FIR:
- dolnoprzepustowego z pasmem przenoszenia do 40 Hz dla sygnału próbkowanego [math]256[/math] Hz, tak aby dla częstości powyżej 45 Hz jego tłumienie było nie mniejsze niż 20dB.
Analiza_sygnałów_-_ćwiczenia/Filtry