Systemy liniowe niezmiennicze w czasie

Systemy LTI

System LTI w symulinku

Konstrukacja symulacji

Poznawanie systemów LTI rozpoczniemy do eksperymentów w Simulinku.

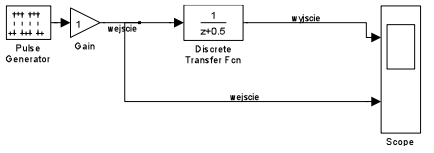
Simulink jest częścią programu Matlab służącą do graficznego budowania modeli i symulacji. Program ten uruchamiamy wydając z konsoli polecenie matlab. Następnie w konsoli Matlaba wpisujemy simulink. Nowy model tworzymy klikając File->New->Model. Korzystając z elementów dostępnych w bibliotece bloczków (Library:simulink) proszę zbudować model przedstawiony na poniższym rysunku.

Potrzebne elementy przeciągamy myszą z biblioteki na okno konstrukcyjne. Odpowiednie elementy znajdują się w:

• Pulse Generator -> Sources
• Gain -> Math Operations
• Discrete transfer Fnc -> Discrete
• Scope -> Sinks

Elementy łączymy przeciągając myszką od wyjścia bloczka do wejścia.

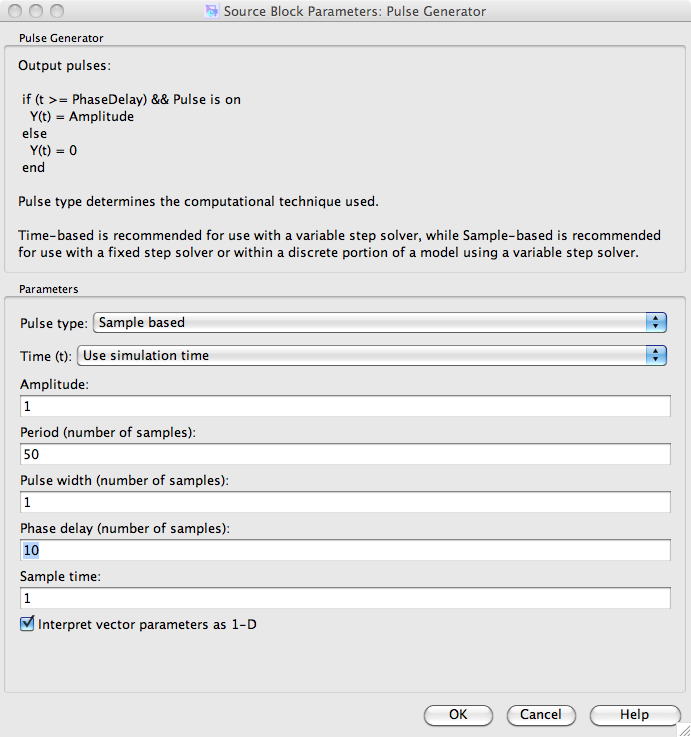
Właściwości bloczków można edytować klikając na nich dwukrotnie. Proszę ustawić własności Pulse Generator zgodnie z poniższym rysunkiem:

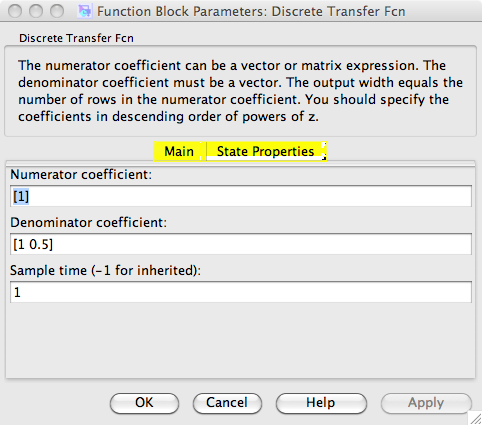
Własności bloczka Discrete Transfer Fnc proszę ustawić jak na rys:

Symulację uruchamiamy klikając Simulation->Start. Otwieramy Scope klikając w niego dwukrotnie i oglądamy wejściowe impulsy i odpowiedzi impulsowe systemu.

Uwaga: Proszę wydłużyć domyślny czas trwania symulacji na 200 jednostek. Można to zrobić w menu: Simulation->Configuration Parameters: Stop Time

Polecenia

1. Co to jest odpowiedź impulsowa?
2. Proszę zbadać, odpowiednio modyfikując podstawowy schemat (bloczki można łatwo powielać przeciągając je na schemacie prawym guzikiem myszy), czy system opisywany przez Transfer Fnc. jest:
   • Niezmienniczy w czasie (w bloczku generatora można zmieniać opóźnienie podania impulsu (Phase delay). Proszę zaobserwować, czy kolejne wersje odpowiedzi impulsowej różnią się od siebie?
   • Liniowy czyli:
     • czy przemnożenie impulsu wejściowego przez skalar (bloczek Gain) powoduje przemnożenie odpowiedzi układu przez ten sam skalar? [math]L(A*s) = A*L(s)[/math]
     • czy jeśli dwa impulsy pojawią się na wejściu na tyle szybko, że reakcja na pierwszy z nich jeszcze nie wygaśnie to czy odpowiedź na drugi z nich po prostu dadaje się do wartości odpowiedzi na pierwszy? [math]L(s_1 + s_2) = L(s_1) +L(s_2)[/math]
3. Proszę zbadać reakcje układu na różna funkcje. W tym celu proszę podmienić bloczek Pulse Generator na Signal Generator. Można przy jego pomocy wpuścić na wejście układu jeden z czterech typów funkcji:
   • sinus
   • prostokąt
   • trójkąt
   • szum

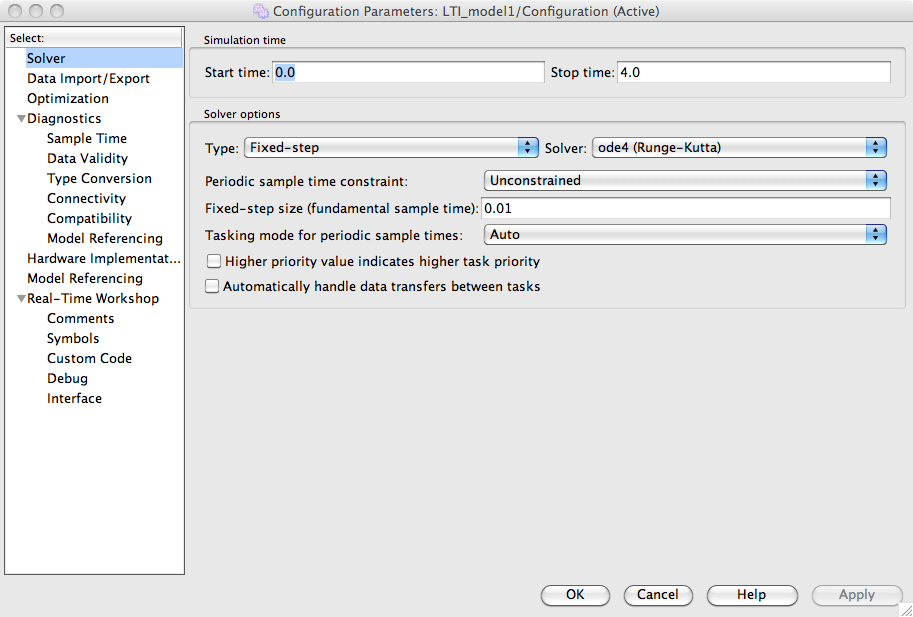
Czy któraś z tych funkcji jest funkcją własną systemu opisywanego przez nasz bloczek Transfer Fnc. ? Uwaga: W bloczkach TransferFuntion i Gain należy zmienić Sample Time na wartość np. 0.01 (taką samą jak w FixedStep Size na poniższym rysunku) Aby dogodnie obserwować powstające sygnały wejściowe i wyjściowe proszę przestawić parametry symulacji na zgodne z rysunkiem:

Splot

Splot

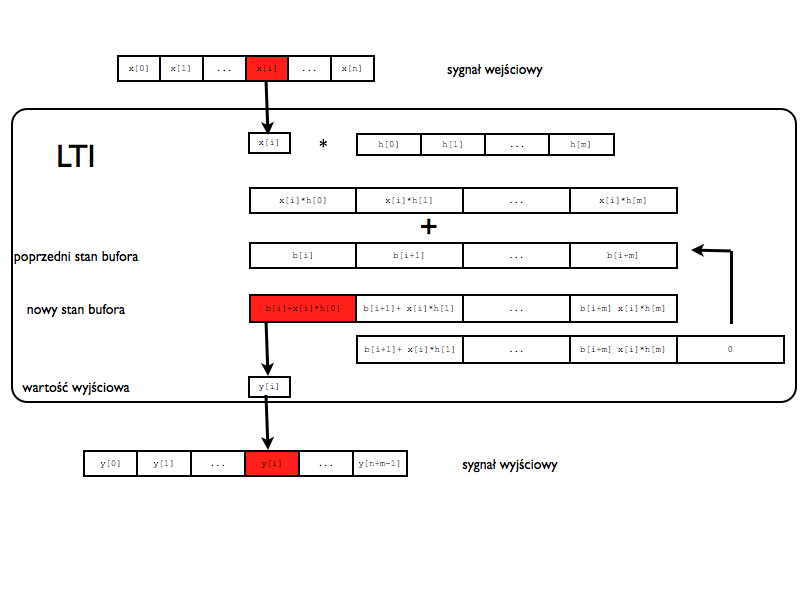
Działanie systemu LTI to splot wejścia z funkcją odpowiedzi impulsowej. Możemy to działanie opisać następującym algorytmem:

1. pobierz z wejścia próbke x[i]
2. przemnóż funkcję odpowiedzi impulsowej przez x[i]
3. otrzymany wektor dodaj do aktualnego bufora wyjściowego.
4. prześlij zerowy element otrzymanego wektora na wyjście.
5. zaktualizuj bufor wartościam z otrzymanego wektora przesuniętymi w lewo o jeden, ostatni element bufora ustaw na 0
6. wykonuj operacje 1-5 dopóki na wejściu są próbki
7. jeśli na wejściu nie ma więcej próbek przekaż na wyjście pozostałą zawartość bufora, oprócz ostatniego elementu

Ideę tą przedstawiono na poniższym rysunki:

Szablon:Wyjaśnienie

Własności splotu

Do obliczania splotu możemy stosować funkcję convolve z modułu scipy.signal. Proszę zaimportować moduł i zapoznać się z dokumentacją tej funkcji.

Splot jest operacją liniową. Proszę zatem sprawdzić numerycznie(tzn. wytworzyć kilkuelementowe wektory x, y, z i wykonać odpowiednie obliczenia), że ma on następujące własności:

• przemienność

[math]x(n)*y(n)=y(n)*x(n)[/math]

• łączność

[math][x(n)*y(n)]*z(n)=x(n)*[y(n)*z(n)][/math]

• rozdzielność względem dodawania

[math]x(n)*[y(n)+w(n)]=x(n)*y(n)+x(n)*w(n)[/math]