Matematyka 1 OO/Badanie przebiegu zmienności funkcji
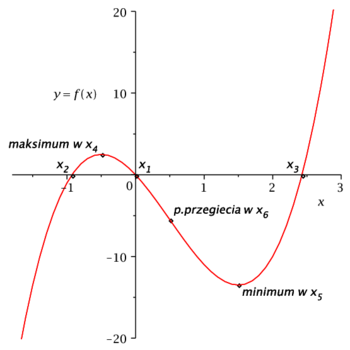
[math]f(x)=4x^3-6x^2-9x[/math]
dziedzina:
dziedziną tej funkcji jest zbiór liczb rzeczywistych [math]{\mathbb R}[/math].
miejsca zerowe [math]f(x)=0[/math]:
- [math] 0=4x^3-6x^2-9x=x(4x^2-6x-9) [/math]
Jednym z miejsc zerowych jest [math]x=0[/math], pozostałe znajdujemy rozwiązując równanie kwadratowe [math]4x^2-6x-9=0[/math]
- [math] \Delta =36+4\cdot 4\cdot 9=36(1+4)=36\cdot 5=6^2\cdot 5 [/math]
- [math] x=\frac{6\pm \sqrt{6^2\cdot 5}}{8}=\frac{3}{4}\pm \frac{3}{4}\sqrt{5} [/math]
miejsca zerowe: [math]x_1=0[/math], [math]x_2=\frac{3}{4}-\frac{3}{4}\sqrt{5}[/math], [math]x_3=\frac{3}{4}+\frac{3}{4}\sqrt{5}[/math].
ekstrema [math]f^{\prime }(x)=0[/math]:
- [math] 0=f^{\prime }(x)=12x^2-12x-9=3(4x^2-4x-3) [/math]
- [math] \Delta =16+4\cdot 4\cdot 3=16+48=64=8^2 [/math]
- [math] x=\frac{4\pm 8}{8} [/math]
ekstrema: [math]x_4=-\frac{1}{2}[/math], [math]x_5=\frac{3}{2}[/math].
punkty przegięcia [math]f^{\prime \prime }(x)=0[/math]:
- [math] 0=f^{\prime \prime }(x)=24x-12=12(2x-1) [/math]
punkt przegięcia [math]x_6=\frac{1}{2}[/math]
wypukłość (wklęsłość) [math]f^{\prime \prime }(x)\gt 0[/math] ([math]f^{\prime \prime }(x)\lt 0[/math]):
funkcja jest wypukła gdy [math]12(2x-1)\gt 0[/math] czyli dla [math]x\gt \frac{1}{2}[/math]
funkcja jest wklęsła gdy [math]12(2x-1)\lt 0[/math] czyli dla [math]x\lt \frac{1}{2}[/math]
granice:
- [math] \lim _{x\rightarrow \pm \infty }f(x)=\lim _{x\rightarrow \pm \infty }(4x^3-6x^2-9x)=\pm \infty [/math]
charakter ekstremów:
- [math] f^{\prime \prime }(x_4)=f^{\prime \prime }\left(-\frac{1}{2}\right)=12\left(2\left(-\frac{1}{2}\right)-1\right) =12(-1-1)=-24\lt 0 [/math]
- [math] f^{\prime \prime }(x_5)=f^{\prime \prime }\left(\frac{3}{2}\right)=12\left(2\left(\frac{3}{2}\right)-1\right) =12(3-1)=24\gt 0 [/math]
[math]\Rightarrow [/math] maksimum w punkcie [math]x_4[/math] i minimum w punkcie [math]x_5[/math].
wartości w punktach charakterystycznych:
- [math] f(x_4)=f\left(-\frac{1}{2}\right)=4/(-2)^3-6/(-2)^2-9/(-2)=-\frac{1}{2}-\frac{3}{2}+\frac{9}{2} =\frac{-1-3+9}{2}=\frac{5}{2} [/math]
- [math] f(x_5)=f\left(\frac{3}{2}\right)=4\cdot 3^3/2^3-6\cdot 3^2/2^2-9\cdot 3/2 =\frac{27}{2}-\frac{27}{2}-\frac{27}{2}=-\frac{27}{2} [/math]
- [math] f(x_6)=f\left(\frac{1}{2}\right)=4/(2)^3-6/(2)^2-9/2=\frac{1}{2}-\frac{3}{2}-\frac{9}{2} =\frac{1-3-9}{2}=\frac{-11}{2} [/math]
wykres:
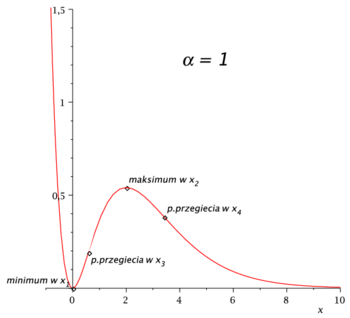
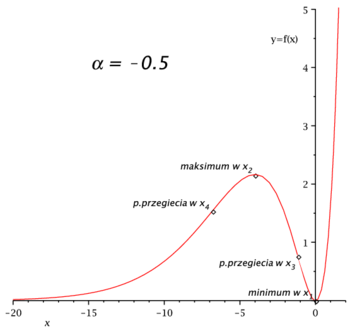
[math]f(x)=x^2e^{-\alpha x}[/math] dla [math]\alpha \ne 0[/math]
dziedzina:
dziedziną tej funkcji jest zbiór liczb rzeczywistych [math]{\mathbb R}[/math].
miejsca zerowe:
- [math] \left(0=x^2e^{-\alpha x}\right)\Leftrightarrow \left(x^2=0\right) \Leftrightarrow \left(x=0\right) [/math]
miejsce zerowe: [math]x_1=0[/math]
ekstrema:
- [math] 0=f^{\prime }(x)=2xe^{-\alpha x}-\alpha x^2 e^{-\alpha x} =x e^{-\alpha x}(2-\alpha x) [/math]
ekstrema: [math]x_1=0[/math], [math]x_2=\frac{2}{\alpha }[/math]
punkty przegięcia:
- [math] 0=f^{\prime \prime }(x)=2 e^{-\alpha x} -2\alpha xe^{-\alpha x}-2\alpha xe^{-\alpha x} +\alpha ^2 x^2 e^{-\alpha x} =e^{-\alpha x}\left(2-4\alpha x+\alpha ^2 x^2\right) [/math]
- [math] \Delta =16\alpha ^2-8\alpha ^2=8\alpha ^2 [/math]
- [math] x=\frac{4\alpha \pm \sqrt{8\alpha ^2}}{2\alpha ^2} =\frac{2\pm \sqrt{2}}{\alpha } [/math]
punkty przegięcia [math]x_3=\frac{2-\sqrt{2}}{\alpha }[/math], [math]x_4=\frac{2+\sqrt{2}}{\alpha }[/math]
wypukłość (wklęsłość):
- [math] \left[e^{-\alpha x}\left(2-4\alpha x+\alpha ^2 x^2\right)\gt 0\right] \Leftrightarrow \left[\left(2-4\alpha x+\alpha ^2 x^2\right)\gt 0\right] [/math]
funkcja jest wypukła gdy [math]x\in (-\infty ,x_3) \cup (x_4,\infty )[/math]
funkcja jest wklęsła gdy [math]x\in (x_3,x_4)[/math]
granice:
- [math] \lim _{x\rightarrow -\infty }f(x)=\lim _{x\rightarrow -\infty }x^2e^{-\alpha x}= \left\lbrace \begin{array}{ll} 0 & dla \alpha \lt 0 \\[8pt] +\infty & dla \alpha \gt 0 \end{array} \right. [/math]
- [math] \lim _{x\rightarrow +\infty }f(x)=\lim _{x\rightarrow +\infty }x^2e^{-\alpha x}= \left\lbrace \begin{array}{ll} +\infty & dla \alpha \lt 0 \\[8pt] 0 & dla \alpha \gt 0 \end{array} \right. [/math]
charakter ekstremów:
- [math] f^{\prime \prime }(x_1)=f^{\prime \prime }(0)=2\gt 0 [/math]
- [math] f^{\prime \prime }(x_2)=f^{\prime \prime }\left(\frac{2}{\alpha }\right)=e^2\left(2-4\alpha \frac{2}{\alpha } +\alpha ^2\left(\frac{2}{\alpha }\right)^2\right) =e^2(2-8+4)=-2e^2\lt 0 [/math]
[math]\Rightarrow [/math] minimum w punkcie [math]x_1[/math] i maksimum w punkcie [math]x_2[/math].
wartości w punktach charakterystycznych:
- [math] f(x_2)=f\left(-\frac{2}{\alpha }\right)=\frac{4}{\alpha ^2}e^{-2} =\left(\frac{2}{\alpha e}\right)^2 [/math]
- [math] f(x_3)=f\left(\frac{2-\sqrt{2}}{\alpha }\right) =\left(\frac{2-\sqrt{2}}{\alpha }\right)^2e^{2-\sqrt{2}} =\frac{6-4\sqrt{2}}{\alpha ^2}\,e^{2-\sqrt{2}} [/math]
- [math] f(x_4)=f\left(\frac{2+\sqrt{2}}{\alpha }\right) =\left(\frac{2+\sqrt{2}}{\alpha }\right)^2e^{2+\sqrt{2}} =\frac{6+4\sqrt{2}}{\alpha ^2}\,e^{2+\sqrt{2}} [/math]
wykres:
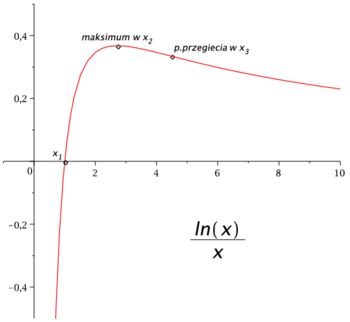
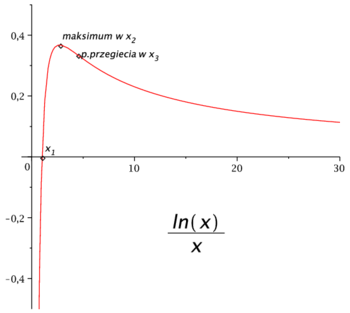
[math]f(x)=\displaystyle \frac{\ln {x}}{x}[/math]
dziedzina:
dziedziną tej funkcji jest zbiór liczb rzeczywistych dodatnich [math]x\in [0,\infty )[/math].
miejsca zerowe:
- [math] \left(0=\frac{\ln {x}}{x}\right)\Leftrightarrow \left(\ln {x}=0\right) \Leftrightarrow \left(x=1\right) [/math]
miejsce zerowe: [math]x_1=1[/math]
ekstrema:
- [math] \left( 0=f^{\prime }(x)=\frac{\frac{1}{x}\cdot x-1\cdot \ln {x}}{x^2} =\frac{1-\ln {x}}{x^2} \right) \Leftrightarrow \left(1-\ln {x}=0\right) \Leftrightarrow \left(\ln {x}=1\right) \Leftrightarrow \left(x=e\right) [/math]
ekstremum: [math]x_2=e[/math]
punkty przegięcia:
- [math] 0=f^{\prime \prime }(x)=\frac{-\frac{1}{x}x^2-2x(1-\ln {x})}{x^4} =\frac{-x-2x+2x\ln {x}}{x^4}=\frac{-3+2\ln {x}}{x^3} [/math]
- [math] \left(0=-3+2\ln {x}\right) \Leftrightarrow \left(x=e^{3/2}=e\sqrt{e}\right) [/math]
punkt przegięcia [math]x_3=e\sqrt{e}[/math].
wypukłość (wklęsłość):
- [math] \left[\frac{-3+2\ln {x}}{x^3}\gt 0\right] \Leftrightarrow \left[x\gt e\sqrt{e}\right] [/math]
funkcja jest wypukła gdy [math]x\in (e\sqrt{e},\infty )[/math]
funkcja jest wklęsła gdy [math]x\in (0,e\sqrt{e})[/math]
granice:
- [math] \lim _{x\rightarrow 0}f(x)=\lim _{x\rightarrow 0}\frac{\ln {x}}{x}=-\infty [/math]
- [math] \lim _{x\rightarrow +\infty }f(x)=\lim _{x\rightarrow +\infty }=\frac{\ln {x}}{x} =\lim _{x\rightarrow +\infty }\frac{(\ln {x})^{\prime }}{(x)^{\prime }} =\lim _{x\rightarrow +\infty }\frac{1}{x} =0 [/math]
charakter ekstremów:
- [math] f^{\prime \prime }(x_2)=f^{\prime \prime }(e)=\frac{-3+2\ln {e}}{e^3}=-\frac{1}{e^3}\lt 0 [/math]
[math]\Rightarrow [/math] maksimum w punkcie [math]x_2[/math].
wartości w punktach charakterystycznych:
- [math] f(x_2)=f(e)=\frac{\ln {e}}{e}=\frac{1}{e} [/math]
- [math] f(x_3)=f(e^{3/2})=\frac{\ln {e^{3/2}}}{e^{3/2}} =\frac{\frac{3}{2}}{e^{3/2}}=\frac{3}{2e\sqrt{e}} [/math]
wykres:
Na lewym (prawym) wykresie lepiej widać zachowanie badanej funkcji
dla małych (dużych) wartości argumentu [math]x[/math].