Fizyka I FM/Kinematyka0
Wektory, układ współrzędnych
Wielkości występujące w przyrodzie możemy podzielić na:
- Skalarne, to jest takie wielkości, które potrafimy opisać przy pomocy jednej liczby (skalara), np. masa, czy temperatura.
- Wektorowe, czyli wielkości które charakteryzujemy podając ich wartość oraz kierunek (np. prędkość, pęd, siła).
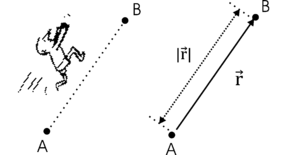
Historycznie pojęcie wektora wywodzi się z potrzeby opisu przemieszczenia. Opisując przemieszczenie jakiegoś obiektu, nie wystarczy podać wielkość tego przemieszczenia (np. 100 m) lecz również jego kierunek — np. obiekt przemieścił się o 100 m. w kierunku północno-zachodnim. Na rysunku %i 1 zaprezentowane są dwa punkty A i B. Przemieszczenie obiektu z punktu A do punktu B można wyrazić symbolicznie przy pomocy strzałki, której początek umieszczony jest w punkcie A, zaś grot w punkcie B. Kierunek wskazywany przez strzałkę określa kierunek przemieszczenia się obiektu, zaś długość strzałki wyraża wielkość przesunięcia. Wielkości, które zachowują się jak opisane powyżej przemieszczenie, nazywamy wektorami.
Graficznie wektory przedstawiane są za pomocą strzałki, pisząc je natomiast możemy użyć wytłuszczonej czcionki, np. a lub też rysować strzałkę nad litera symbolizującą wielkość wektorową, np. [math]\vec{a}[/math]. Często interesuje nas tylko wartość (długość) wektora, którą oznacza się w następujący sposób: [math]|\textbf{a}|[/math], a lub [math]|\vec{a}|[/math].
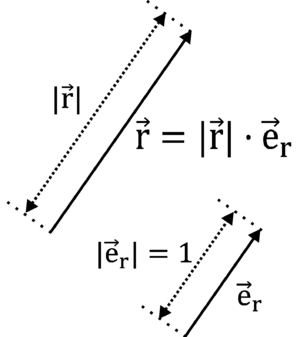
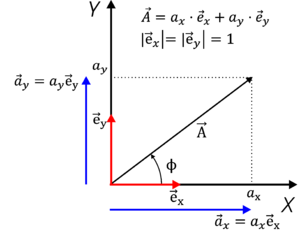
Przy opisie wektora wygodnie jest wprowadzić pojęcie wektora jednostkowego (wersora), to jest wektora o określonym kierunku i długości równej 1. Na rysunku %i 2 zaprezentowano wektor [math]\vec{e}_r[/math] o długości równej 1 i kierunku równoległym do wektora [math]\vec{r}[/math]. Wektory najczęściej wiążemy z pewnymi układami współrzędnych. Na rysunku %i 3 zaprezentowano wektor [math]\vec{A}[/math] w kartezjańskim układzie współrzędnych, utworzonym przez dwie prostopadłe do siebie osie. W fizyce stosuje się również inne układu współrzędnych (np. biegunowe, walcowe, sferyczne), w których opis rozpatrywanego zagadnienia może się uprościć. W kartezjańskim układzie współrzędnych, współrzędne wektora [math]\vec{A}[/math]wynoszą (patrz rysunek %i 3):
Z kolei mając współrzędne wektora, można określić jego długość i kierunek (rozumiany tutaj jako kąt pomiędzy wektorem a wyszczególnioną osią układu współrzędnych):
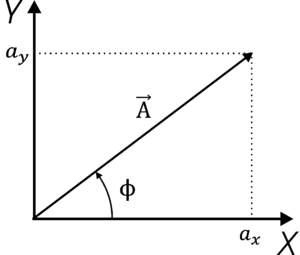
W układzie współrzędnych wektor można również rozłożyć na składowe, czyli rzuty wektora na osie układu współrzędnych, co bardzo często upraszcza dalsze rozwiązywanie danego problemu. Na rysunku %i 4 zaprezentowano dwuwymiarowy układ kartezjański, w którym wprowadzono dwa wersory [math]\vec{e}_x[/math] i [math]\vec{e}_y[/math] równoległe do osi układu oraz rozłożono wektor [math]\vec{A}[/math] na dwie składowe: [math]\vec{a}_x=a_x\vec{e}_x[/math] oraz [math]\vec{a}_y=a_y\vec{e}_y[/math].
Kinematyka — opis ruchu
Na początku przytoczymy definicję kilku pojęć, które pełnią niezwykle ważną role nie tylko w kinematyce lecz również w całej fizyce.
- Punkt materialny — ciało, którego rozmiary można zaniedbać w rozpatrywanym zagadnieniu (np. rozmiary Ziemi w porównaniu z promieniem orbity Ziemi w jej ruchu dookoła Słońca można pominąć), zaś stan określany jest wyłącznie poprzez położenie. Zazwyczaj obdarzony jest masą.
- Ruch — zmiana położenia ciała względem wybranego układu odniesienia.
- Układ odniesienia — ciało, które wyznaczamy jako punkt odniesienia, w dalszej części materiałów będzie oznaczany dużą literą 0.
- Układ współrzędnych — ilościowy sposób określenia położenia ciała. Układ współrzędnych zawsze związany jest z układem odniesienia.
Położenie dowolnego punktu P określa jednoznacznie wektor [math]\vec{r}=\vec{0P}[/math], czyli taki, którego początek umieszczony jest w układzie odniesienia, zaś koniec wskazuje na punkt materialny. Pojęcie ruchu jest nierozerwalnie związane z pojęciem układu odniesienia, względem którego ruch ten zachodzi. Dla opisu ruchu punktu musimy podać zbiór wielkości, które pozwalają na jednoznaczne określenie położenie punktu względem wybranego układu odniesienia w dowolnej chwili czasu. Tym zbiorem wielkości jest wektor [math]\vec{r}[/math], który najczęściej podajemy we współrzędnych kartezjańskich: [math]\vec{r}(t)=[x(t), y(t), z(t)][/math]. W zależności od rozpatrywanego problemu, w fizyce wykorzystuje się również inne układy współrzędnych (np. biegunowy, walcowy, sferyczny), w których dane zagadnienie może ulec uproszczeniu. Kolejne punkty, przez które przechodzi poruszający się punkt tworzą w przestrzeni krzywą, którą nazywamy torem ruchu.
Prędkość
Prędkość średnia:
gdzie:
- [math]\Delta t = t_2 - t_1[/math]
- [math]\Delta \vec{r} = \vec{r}(t_2) - \vec{r}(t_1)[/math]
Przykładem prędkości średniej jest prędkość samochodu np. na trasie Warszawa - Łódź. Odległość między tymi miejscowościami wynosi [math]|\vec{r}|[/math] = 130 km. Jeśli samochód przebył tę odległość w ciągu [math]\Delta t[/math] = 1 godziny, to jego średnia prędkość na trasie wyniosła: [math]|\vec{V}_s|[/math] = 130km/h.
Prędkość chwilowa:
Rozważmy ponownie samochód jadący na trasie Warszawa - Łódź. Średnia prędkość tego samochodu wyniosła [math]|\vec{V}_s|[/math] = 130km/h, jednakże w trakcie jazdy samochód mógł przyspieszać lub zwalniać. Dokładniejszą wartość prędkości uzyskamy wtedy, gdy będziemy analizowali ruch samochodu w kilku przedziałach czasowych, np. co 15 minut. Dlaczego jednak nie można by dokonywać pomiaru prędkości na podstawie przebytej drogi nie w ciągu 15 minut, tylko 1 minuty, a może 1 sekundy, a może w jeszcze krótszym czasie. Idąc tą drogą rozumowania dochodzimy do definicji prędkości chwilowej, którą jest następująca granica:
Taką granicę nazywamy pochodną położenia po czasie i oznaczamy w następujący sposób:
W układzie kartezjańskim wektor prędkości wyrażony jest w następujący sposób:
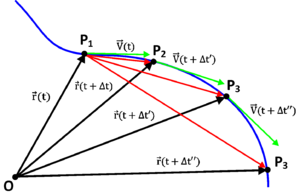
Wektor prędkości chwilowej jest zawsze styczny do toru. Można to zauważyć na rysunku %i 5, prześledziwszy jak zmienia się kierunek wektora [math]\Delta\vec{r}[/math] dla [math]\Delta t\rightarrow 0[/math].
Przyspieszenie:
Przyspieszenie średnie
Przyspieszenie średnie jest to przyrost prędkości w pewnym odstępie czasu:
gdzie:
- [math]\Delta t = t_2 - t_1[/math]
- [math]\Delta \vec{V} = \vec{V}(t_2) - \vec{V}(t_1)[/math]
Przyspieszenie chwilowe
Analogicznie do prędkości chwilowej możemy również zdefiniować przyspieszenie chwilowe, jako granicę następującego wyrażenia:
W układzie kartezjańskim wektor chwilowego przyspieszenie wyrażony jest w następujący sposób:
Wektor przyspieszenia rozkładamy często na sumę dwóch prostopadłych do siebie wektorów. ten o kierunku stycznym do toru nazywamy przyspieszeniem stycznym (jest ono zawsze, gdy zmienia się wartość wektora prędkości). Drugi wektor, o kierunku prostopadłym (normalnym) do toru nazywamy przyspieszeniem normalnym — jest ono związane ze zmianami kierunku wektora prędkości.
Klasyfikacja ruchu.
Na podstawie kształtu ruchu, ruchy dzielimy na:
- Prostoliniowe,
- Krzywoliniowe (np. ruch ruch po okręgu, elipsie, paraboli itd.).
Ruch można też klasyfikować na podstawie charakteru wektorów położenia, prędkości i przyspieszenia od czasu. Podstawowy podział to:
- Ruchy jednostajne, w których wartość wektora prędkości jest stała przez cały czas trwania ruchu (inaczej: droga w każdym przedziale czasu jest wprost proporcjonalna do długości tego przedziału).
- Ruchy zmienne — każdy ruch, który nie jest ruchem jednostajnym, czyli w którym wektor prędkości zmienia wartość.
- ruchy jednostajnie zmienny — to szczególna kategoria ruchu, w którym wektor przyspieszenia stycznego ma stałą wartość. Innymi słowy nie ulega zmianie wartość wektora prędkości, natomiast zmienia się kierunek wektora prędkości.
Ponadto możemy mówić o
- Ruchach przyspieszonych i opóźnionych.
- Okresowych (periodycznych) i nieokresowych.
Zadanie 1
Odcinek o stałej długości porusza się tak, że jego punkty końcowe A i B ślizgają się p osiach x i y pewnego prostokątnego układu współrzędnych. Jaki tor zakreśla punkt M dzielący odcinek AB w stosunku a:b? jaki kształt ma tor dla a=b?.