Fizyka I FM/Kinematyka4

Dwa układy odniesienia będące w ruchu.

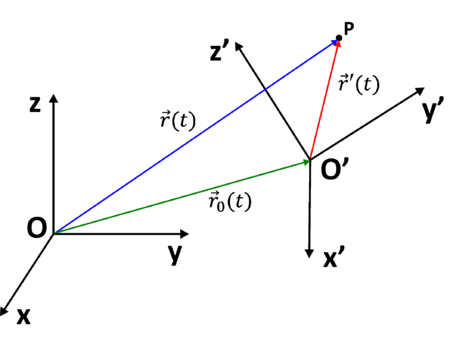
Wszystkie wielkości kinematyczne charakteryzujące ruch ciała zależą od wyboru układu odniesienia, w którym opisujemy ruch ciała. Na rysunku %i 1 zaprezentowano:

• Układ współrzędnych obserwatora 1 — U o początku w punkcie O i osiach x, y, z.
• Układ współrzędnych obserwatora 2 — U' o początku w punkcie O' i osiach x', y', z'.

Wektor [math]\vec{r}_0[/math] opisuje położenie punktu O' w układzie U, zaś kąty jakie tworzą osie układu U — x, y, z z osiami x', y', z', nazwiemy odpowiednio [math]\alpha[/math], [math]\beta[/math], [math]\gamma[/math]. Układ U' może poruszać się względem układu U, wtedy oczywiście [math]\vec{r}_0[/math], [math]\alpha[/math], [math]\beta[/math], [math]\gamma[/math] zmieniają się w czasie. Jeśli U' porusza się względem U ruchem postępowym (bez obrotów), zmianie ulega tylko wektor [math]\vec{r}_0[/math]. Jeśli układ U' obraca się, ale jego początek w punkcie O' pozostaje w spoczynku względem układu U, wtedy zmianie w czasie ulegają kąty [math]\alpha[/math],[math]\beta[/math], [math]\gamma[/math]. Dowolny ruch układu U' względem U jest złożeniem obydwu wymienionych ruchów, czyli postępowego i obrotowego.

Zachodzi następujące twierdzenie:

Na to, aby obserwatorzy w dwóch różnych układach odniesienia przypisywali ruchowi tego samego ciała w każdej chwili czasu identyczne wektory przyspieszenia, potrzeba i wystarcza, aby układy te poruszały się względem siebie ruchem postępowym jednostajnym prostoliniowym.

Możemy podzielić układy odniesienia na rozłączne klasy układów. W jednej klasie znajdują się te wszystkie układy odniesienia, w których obserwatorzy przypisują temu samemu poruszającemu się ciału jednakowe przyspieszenia. Są to więc układy odniesienia, które poruszają się względem siebie ruchem postępowym jednostajnym prostoliniowym. Układy należące do tej klasy nazywamy układami dynamicznie równoważnymi.

Niech układ U' porusza się względem U ruchem postępowym. Opis ruchu punktu P w układzie U można dokonać w następujący sposób:

[math]\left\{\begin{array}{l} \vec{r}=\vec{r}_0 + \vec{r'}\\ \\ \vec{V}=\vec{V}_0 + \vec{V'}\\ \\ \vec{a}=\vec{a}_0 + \vec{a'}\\ \end{array}\right. [/math]

gdzie:

• [math]\vec{V}=\frac{d\vec{r}}{dt}[/math] — prędkość punktu P w układzie U,
• [math]\vec{V}'=\frac{d\vec{r'}}{dt}[/math] — prędkość punktu P w układzie U',
• [math]\vec{V}'_0=\frac{d\vec{r_0}}{dt}[/math] — wektor prędkości punktu O' w układzie U, czyli prędkość ruchu postępowego układu U' względem układu U.
• [math]\vec{a}=\frac{d\vec{V}}{dt}[/math] — przyspieszenie punktu P w układzie U,
• [math]\vec{a'}=\frac{d\vec{V'}}{dt}[/math] — przyspieszenie punktu P w układzie U',
• [math]\vec{a_0'}=\frac{d\vec{V_0'}}{dt}=\frac{d^2\vec{r_0}}{dt^2}[/math] — przyspieszenie ruchu postępowego układu U' względem U.

Jeśli [math]\vec{a_0}=0[/math] to ruch układu U względem układu U' jest ruchem jednostajnym prostoliniowym i wtedy:

[math]\vec{a_0'}=\vec{a}[/math]

Jeśli osie układów U i U' są równoległe, to:

[math]\left\{\begin{array}{lcr} x = x_0 + x', & V_x = V_0 + V_x', & a_x = a_0 + a'_x \\ \\ y = y_0 + y', & V_y = V_0 + V_y', & a_y = a_0 + a'_y \\ \\ z = z_0 + y', & V_z = V_0 + V_z', & a_z = a_0 + a'_z \\ \end{array}\right. [/math]

Zadanie 1.

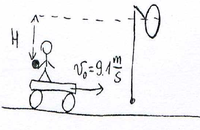
Ilustracja do zadania 1.

Człowiek porusza się na drezynie za stała prędkością [math]v_0=\unit{9,1}{m/s}[/math]. Chce przerzucić piłkę przez obręcz umocowaną do pręta przy torach i będącą [math]H=\unit{4,9}{m}[/math] powyżej wysokości jego reki, w taki sposób, aby piłka poruszała się z prędkością poziomą w momencie przechodzenia przez obręcz. Rzuca piłkę z prędkością [math]v’=\unit{10,8}{m/s}[/math] w stosunku do własnego układu odniesienia.

1. Jaka powinna być składowa pionowa prędkości początkowej piłki?
2. Po jakim czasie piłka przejdzie przez obręcz?
3. W jakiej odległości od obręczy liczonej poziomo, człowiek musi wykonać rzut?
4. Jaki jest kierunek prędkości początkowej piłki w układzie odniesienia człowieka?
5. Jaki jest kierunek prędkości początkowej piłki w układzie obserwatora stojącego przy torach?

Zadanie 2.

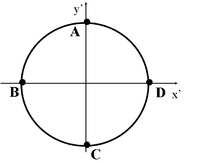
Ilustracja do zadania 2.

Koło wagonu kolejowego toczy się bez poślizgu po prostej szynie tak, że prędkość jego środka względem spoczywającego obserwatora (układ U) wynosi [math]\vec{V}_0 = \overrightarrow{const}[/math]. Oblicz prędkości chwilowe punktów A, B, C i D w układzie U i w układzie U’ o środku w środku koła. Wyznacz równanie ruchu, toru.