TI/Grafy

Krótki wstęp do teorii grafów

Graf

Graf jest to zbiór wierzchołków [math]V[/math] i zbiór krawędzi [math]E[/math]. Każdy wierzchołek [math] v\in V[/math] to po prostu jakiś obiekt, najczęściej po prostu etykieta. Natomiast każda krawędz [math] e\in E[/math] to para wierzchołków, czyli [math]e = (v_1, v_2)[/math]. Istnienie krawędzi oznacza istnienie relacji pomiędzy tymi dwoma wierzchołkami.

Jedna krawędź nie może związać ze sobą więcej niż dwóch wierzchołków. Dwa wierzchołki mogą być ze sobą związane więcej niż jedną krawędzią.

Definicja matematyczna

Grafem nazywamy parę uporządkowaną [math] G =\lt V, E \gt [/math] przy czym:

• [math]V[/math] — zbiór wierzchołków grafu,
• [math]E[/math] — zbiór krawędzi grafu, każde [math]e \in E[/math] to para elementów [math]V[/math], [math]e=(v_1, v_2), v_1 \in V, v_2 \in V[/math].

Krawędzie skierowane i nieskierowane

Są dwa typy grafów:

• graf nieskierowany, w którym krawędzie nie mają kierunku, czyli krawędź [math]e = (v_1, v_2)[/math] jest tym samym co krawędź [math]e' = (v_2, v_1)[/math]. Przykładem takiego grafu może być graf osób gdzie krawędzie reprezentują spotkania. Ponieważ jeśli A. spotkał B., to i B. spotkał A., więc graf jest nieskierowany.
• graf skierowany, w którym rozróżniamy krawedź [math](v_1, v_2)[/math] i [math](v_2, v_1)[/math]. Przykładem takiego grafu może być graf osób i tego czy się lubią — jeśli A. lubi B., to B. może też lubić A., ale niestety nie musi.

Jeśli [math](v_1, v_2)[/math] jest krawędzią w grafie skierowanym, to mówimy, że krawędź wychodzi z wierzchołka [math]v_1[/math] i wchodzi do wierzchołka [math]v_2[/math].

Sąsiedztwo

Jeżeli [math](u, v)[/math] jest krawędzią grafu, to mówimy, że wierzchołek [math]v [/math] jest sąsiadem wierzchołka [math]u[/math].

Jeżeli graf jest nieskierowany, relacja sąsiedztwa jest symetryczna. Jeżeli graf jest skierowany, relacja sąsiedztwa nie musi być symetryczna. W grafie skierowanym, jeżeli [math]v [/math] jest wierzchołkiem sąsiadującym z [math] u[/math], relacja ta jest często zapisywana jako [math] u\rightarrow v[/math].

Stopień wierzchołka

Stopniem wierzchołka jest liczba krawędzi wychodzących lub wchodzących do tego wierzchołka. W przypadku grafu nieskierowanego, kierunek nie ma znaczenia, więc jest to po prostu liczba krawędzi łączących dany wierzchołek z innymi.

Stopień wejściowy

W grafie skierowanym — liczba krawędzi wchodzących do wierzchołka.

Stopień wyjściowy

W grafie skierowanym — liczba krawędzi wychodzących z wierzchołka.

Oczywiście stopień wejściowy plus stopień wyjściowy muszą w sumie dać stopień wierzchołka.

Ścieżka

Ścieżka (droga) długości [math]k[/math] z wierzchołka [math]u[/math] do wierzchołka [math]u'[/math] w grafie [math]G=(V,E)[/math] jest ciagiem wierzchołków [math]\lt v_0, v_1,..,v_k\gt [/math] , takich że [math] u = v_0[/math] i [math] u'=v_k[/math], a pary [math](v_{i-1}, v_i)[/math] należą do zbioru krawędzi [math]E[/math] dla wszystkich [math]i[/math] od 1 do [math]k[/math].

Długość ścieżki jest liczbą krawędzi w ścieżce.

Ścieżka zawiera wierzchołki [math]v_0[/math], [math]v_1[/math],…, [math]v_k[/math] i krawędzie [math](v_0, v_1)[/math], [math](v_1, v_2)[/math],…, [math](v_{k-1}, v_k)[/math].

Ścieżka prosta

Ścieżka, której wszystkie wierzchołki są różne.

Osiągalność

W grafie [math]G=(V,E)[/math] o wierzchołku [math]v_1[/math] możemy powiedzieć, że jest osiągalny z wierzchołka [math]v_0[/math], jeżeli istnieje ścieżka [math]p[/math] z [math]v_0[/math] do [math]v_1[/math].

Cykl

W grafie skierowanym

W grafie skierowanym [math]G = (V,E)[/math] ścieżka [math]\lt v_0,v_1,\ldots,v_k\gt [/math] tworzy cykl, jeżeli [math]v_0=v_k[/math] i ścieżka zawiera co najmniej jedną krawędź.

Pętla jest cyklem o długości jeden.

Prosty

Cykl jest prosty jeżeli [math]v_1,v_2,\ldots,v_k[/math] są różne.

W grafie nieskierowanym

W grafie nieskierowanym [math]G = (V,E)[/math] ścieżka [math]\lt v_0,v_1,\ldots,v_k\gt [/math] tworzy cykl, jeżeli [math]v_0=v_k[/math], [math]v_1,v_2,\ldots,v_k[/math] są różne i [math]k \geq 2[/math].

Graf spójny

Graf nieskierowany jest spójny, jeżeli każda para wierzchołków jest połączona ścieżką.

Graf skierowany jest silnie spójny, jeżeli każde dwa wierzchołki są osiągalne jeden z drugiego.

Graf pełny

Graf nieskierowany, w którym każda para wierzchołków połączona jest krawędzią.

Graf dwudzielny

Graf nieskierowany, którego zbiór wierzchołków można podzielić na dwa rozłączne zbiory tak, że krawędzie nie łączą wierzchołków tego samego zbioru.

Pojęcie to można uogólnić na trzy i więcej zbiorów.

Graf acykliczny

Graf niezawierający cykli.

Graf wolny

Acykliczny graf nieskierowany.

Jak skonstruować graf skierowany z nieskierowanego i odwrotnie

W przypadku grafu nieskierowanego, każdą jego krawędź nieskierowaną [math](u,v)[/math] zamieniamy na dwie skierowane gałęzie [math](u,v)[/math] i [math](v,u)[/math].

Konstruując wersję nieskierowaną grafu skierowanego, usuwamy wszystkie pętle i zamieniamy wszystkie skierowane krawędzie na nieskierowane.

Zastosowania

Grafy ze względu na swoją ogólność są jednymi z najbardziej powszechnych modeli różnych strukur — zarówno tych stworzonych przez człowieka, jak i tych stworzonych przez naturę. Używa się ich do modelowania związków a także procesów dynamicznych w systemach fizycznych, biologicznych i społecznych, ale także i w ligwistyce.

Zadania

Zadanie 1

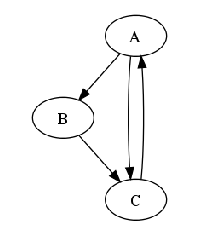
Który z przedstawionych grafów na rysunkach Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 jest grafem wolnym?

Jakie są cechy grafu wolnego?

Zadanie 2

Który z przedstawionych grafów Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 jest grafem pełnym?

Jakie są cechy grafu pełnego?

Zadanie 3

Wypisz sąsiadów wierzchołka(ów) o najwyższym stopniu w grafach na rysunkach Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6.

Zadanie 4

• Dla grafu na rysunku Figure 1:
  • Wypisz jakie wierzchołki są nieosiągalne dla wierzchołków 3 i 7.
  • Które wierzchołki nie mają żadnego osiągalnego wierdzchołka?
  • Jaka jest największa możliwa długość ścieżki?
• Dla grafu na rysunku Figure 5:
  • Czy graf ma wierzchołek, dla którego wszystkie inne wierzchołki są osiągalne?
  • Czy graf ma wierzchołek, który nie ma żadnego osiągalnego wierzchołka?
• Dla grafu na rysunku Figure 6
  • Wypisz najdłuższą możliwą ścieżkę.

Zadanie 5

Które z grafów przedstawionych na rysunkach Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 zawierają cykle?

Moduł przedstawiający reprezentację abstrakcyjnego grafu

Poniższy tekst programu jest autorstwa Niko Wilberta.

#!/usr/bin/env python
# -*- coding: utf-8 -*-

"""
This module contains all elements for an abstract graph representation.

Written by Niko Wilbert for the G-Node Python Winter School 2010.
"""

class Node(object):
    """Base class for nodes.
    
    To add additional data attributes to nodes you can derive subclasses.
    """
    
    def __init__(self):
        """Initialize the node."""
        self._out_edges = []  # outgoing edges
        self._in_edges = []  # incoming edges
        
    @property
    def out_edges(self):
        return self._out_edges
    

class Edge(object):
    """Edge class.
    
    This class also registers itself with the affected nodes, so it sits
    between Node and Graph in the hierarchy. The head and tail can also be
    None.
    """
    
    def __init__(self, head, tail):
        """Initialize the edge.
        
        head, tail -- The end and starting node of this edge, or can be None.
        """
        self._head = head
        if head is not None:
            head._in_edges.append(self)
        self._tail = tail
        if tail is not None:
            tail._out_edges.append(self)
        
    def _set_head(self, head):
        """Set the head and register this in the nodes as well.
        
        The head can also be None, then the edge is unregistered.
        """
        if self._head is not None:
            self._head._in_edges.remove(self)
        self._head = head
        if head is not None:
            self._head._in_edges.append(self)
            
    def _set_tail(self, tail):
        """Set the tail and register this in the nodes as well.
        
        The tail can also be None, then the edge is unregistered.
        """
        if self._tail is not None:
            self._tail._out_edges.remove(self)
        self._tail = tail
        if tail is not None:
            self._tail._out_edges.append(self)
    
    # use these public properties
    head = property(lambda self: self._head, _set_head)
    tail = property(lambda self: self._tail, _set_tail)

    def clear_nodes(self):
        """Clear the node references."""
        self._set_tail(None)
        self._set_head(None)


class GraphException(Exception):
    """Base Exception for Graph."""
    pass


class NoPathGraphException(GraphException):
    """Exception signaling that there is no path between nodes."""
    pass


class Graph(object):
    """Class to represent a complete graph with nodes and edges.
    
    Note that this class does not support nodes which do not belong to any
    edge (internally only edges are stored).
    """
    
    def __init__(self, edges=None):
        self._edges = set()
        if edges:
            for edge in edges:
                self.add_edge(edge)
                
    @property
    def edges(self):
        """Return list of the edges in this graph."""
        return self._edges
    
    @property
    def nodes(self):
        """Return set of nodes in this graph."""
        nodes = set()
        for edge in self._edges:
            nodes.add(edge.head)
            nodes.add(edge.tail)
        return nodes
        
    def add_edge(self, edge):
        """Add an edge to the graph."""
        self._edges.add(edge)
        
    def remove_edge(self, edge):
        """Remove an edge from the graph."""
        edge.clear_nodes()
        self._edges.remove(edge)

Zadania

Zadania są autorstwa Niko Wilberta i Bartosza Teleńczuka.

Powyżej przedstawiona jest implementacja klas reprezentujących obiekt. Na kartce dokonaj analizy kodu.

1. Wypisz wszystkie nazwy klas, ich metody i własności publiczne (czyli te, które nie zaczynają się od podkreślenia). Spróbuj zrozumieć jakie jest ich wszystkich działanie (przeczytaj docstringi!). Nie zawahaj się zapytać ćwiczeniowca, jeżeli masz jakieś wątpliwości. Znajdź ewentualne błędy implementacji. Jeżeli składnia @property jest dla Ciebie dziwna lub niezrozumiała, przeczytaj o dekoratorach i property.
2. Zastanów się, jak poszczególne klasy są ze sobą związane (dziedziczenie kontra wykorzystanie explicite cudzych metod). Narysuj prosty diagram.
3. Korzystając z klasy Graph zaimplementuj graf przedstawiony na rysunku Figure 5 (nr wierzchołka zmień na nazwę np. 1 na N1) i Figure 7.

Algorytm szukający najkrótszej ścieżki

Autor Niko Wilbert

Krótkie wprowadzenie do problemu poszukiwania najkrótszej ścieżki można znaleźć tu

#!/usr/bin/env python
#coding=utf-8

from heapq import heappop, heappush

def shortest_path(start_node, end_node, weight_func=lambda edge: 1):
    """Return the shortest path and its overall weight.
    
    weight_func -- Functions that maps an edge to a weight value, the
        default function maps all edges to 1.
    """
    ## this is basically Dijkstra's algorithm
    # store the shortest path to all nodes,
    # the value tuples contain the path length and the previous node 
    shortest_paths = {start_node: (0, None)}
    # we use this list as a priority cue with heapq
    # the tuples contain the overall path length and the edge itself
    edge_heap = []
    for edge in start_node.out_edges:
        heappush(edge_heap, (weight_func(edge), edge))
    while edge_heap:
        path_weight, edge = heappop(edge_heap)
        if ((edge.head not in shortest_paths) or
            (shortest_paths[edge.head][0] > path_weight)):
            shortest_paths[edge.head] = (path_weight, edge)
            # if we already visited this node then there may be edge
            # duplicates in the heap, but this is no problem because
            # the newer edges are guaranteed to come first
            for out_edge in edge.head.out_edges: 
                heappush(edge_heap, (path_weight + weight_func(out_edge),
                                        out_edge))
    if end_node not in shortest_paths:
        err = ("The is no connection from node %s" % str(start_node) +
                " to node %s." % str(end_node))
        raise NoPathGraphException(err)
    # assemble the shortest path from end to start
    path_weight = shortest_paths[end_node][0]
    path_edges = [shortest_paths[end_node][1]]
    current_node = path_edges[-1].tail
    while current_node is not start_node:
        path_edges.append(shortest_paths[current_node][1])
        current_node = path_edges[-1].tail
    return path_edges[::-1], path_weight

Zadania

Korzystając z kodu klasy Graph oraz shortest_path() napisz aplikację do planowania podróży. W tej aplikacji poszczególne miasta bedą reprezentowane jako węzły w grafie, a krawędzie pomiędzy węzłami będą reprezentowały możliwe środki komunikacji.

1. Napisz klasę CityNode, która roszerza klasę Node o nazwę (miasta), która definiowana jest przy inicjalizacji klasy.
2. Napisz klasę TransportationEdge rozszerzającą klasę Edge. Krawędzie powinny być skierowane i obarczone dwoma rodzajami wag — czasem podróży i kosztem; klasa powinna też zawierać pole description zawierające krótki opis środka transportu.
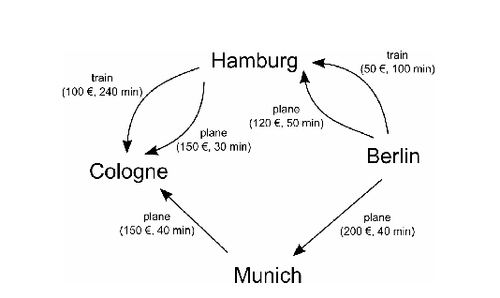
3. Zaimplementuj graf pokazany na rysunku Figure 8. Zastanów się pierw jakie operacje powinny być udostępnione przez ten graf, jakie może być jego zastosowanie.
4. Chciałbyś znaleźć najkrótszą drogę pomiędzy Berlinem a Kolonią. Funkcja shortest_path() znajduje najkrótszą drogę w grafie. Korzystając z tej funkcji rozszerz klasę Graph o metody poszukujące najkrótszej i najtańszej drogi.
5. Znajdź najkrótszą drogę między Berlinem a Kolonią.