Elektroencefalografia/Metody analizy sygnałów EEG - przykłady
Spis treści
Desynchronizacja i synchronizacja EEG związana z bodźcem (ERD/ERS)
W rozdziale dotyczącym analizy sygnałów EEG w dziedzinie czasu opisaliśmy klasyczne podejście do badania odpowiedzi mózgu na bodźce, tj. potencjały wywołane. Ale:
- W podobny sposób badać możemy też odpowiedzi na bodźce wewnętrzne, jak na przykład dobrowolna decyzja machnięcia palcem. Wtedy badanie systematycznych zmian w EEG/MEG również przed bodźcem nie będzie zaprzeczać przyczynowości.
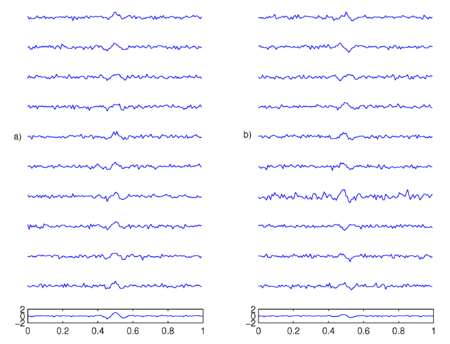
- Nie wszystkie systematyczne zmiany w sygnale będą widoczne po uśrednieniu -- na przykład aktywność występująca po każdym bodźcu w ściśle określonym paśmie częstości i zawsze z tym samym opóźnieniem, ale z przypadkowymi fazami, będzie znikać po uśrednieniu odpowiednio dużej ilości przebiegów (rys. 1).
Opisane powyżej odpowiedzi związane z bodźcem bez zachowania stałych zależności fazowych nazywamy aktywnością indukowaną (induced), w odróżnieniu od opisanej w poprzednim rozdziale aktywności wywołanej (evoked).
Definicja
Klasycznymi miarami takich odpowiedzi są desynchronizacja i synchronizacja EEG związana z bodźcem (event-related desynchronization and synchronization, ERD/ERS). Jest to spadek (desynchronizacja, ERD) lub wzrost (synchronizacja, ERS) mocy w określonym paśmie częstości, występujący w okolicy czasowej zdarzenia, mierzony jako procentowa zmiana w stosunku do odcinka sygnału odzwierciedlającego czynność mózgu nie związaną z bodźcem (Pfurtscheller i Arnibar, 1979). Względna zmiana mocy może przyjmować wartości dodatnie i ujemne. Tradycyjnie ujemne wartości nazywane są ERD, a dodatnie ERS. ERD/ERS można wyrazić następującym wzorem:
gdzie:
- [math]P_f(t)[/math] - średnia moc chwilowa w paśmie częstości [math]f[/math]. Uśrednianie przebiega po realizacjach.
- [math]R_f[/math] - średnia moc w paśmie [math]f[/math] w okresie referencyjnym. Uśrednianie przebiega po realizacjach i po czasie trwania okresu referencyjnego.
Interpretacja fizjologiczna
Tradycyjne nazwy ERD i ERS mają swoje źródło w fizjologicznej interpretacji zmian mocy sygnału w określonych pasmach. Wspominaliśmy już w naszym podęczniku Biofizyczne podstawy generacji sygnałów EEG[1]), że źródłem mierzalnego na zewnątrz głowy sygnału elektrycznego lub magnetycznego jest synchroniczna aktywność wielu neuronów (głównie piramidalnych kory). Szacuje się, że wpływ na wielkość sygnału EEG lub MEG ma głównie stopień synchronizacji neuronów wytwarzających ten sygnał, a w drugiej kolejności ich ilość. Tak więc wzrost mocy w pewnym paśmie (np. alfa ERS) interpretowany jest jako wzrost synchronizacji aktywności neuronów generujących aktywność EEG w tym paśmie, zaś spadek mocy (np. alfa ERD) interpretowany jest jako spadek synchronizacji neuronów generujących aktywność EEG w tym paśmie częstości. Przy takiej interpretacji należy pamiętać o skali w jakiej dokonywany jest pomiar. Zarówno elektrody EEG jak i sensory MEG mierzą sygnały średnie pochodzące od olbrzymich ilości neuronów. Zatem spadek mocy w tym sygnale odpowiada desynchronizacji w skali globalnej (rzędu 106 - 107 neuronów). Nie musi on jednak implikować desynchronizacji w skali mikro. Łatwo możemy wyobrazić sobie następujący model: w okresie referencyjnym mamy do czynienia ze słabo związaną oscylującą meta-populacją neuronów, która pod wpływem bodźca rozpada się na wiele mniejszych populacji neuronów, z których każda z osobna może mieć zwiększoną synchronizację wewnętrzną, ale pomiędzy sobą te populacje są rozsynchronizowane.
Klasyczne metody liczenia ERD/ERS

a) Przykładowy zapis EEG jednej z [math]N[/math] realizacji
b) przefiltrowany sygnał EEG w wybranym paśmie (tutaj: [15 25] Hz)
c) przefiltrowany sygnał podniesiony do kwadratu — w ten sposób uzyskujemy przebieg mocy pasmowej w czasie
d) uśredniony po realizacjach przebieg mocy pasmowej w czasie
e) wygładzony przebieg z d) za pomocą średniej biegnącej (tutaj okienko 0.25 s) czerwone pionowe linie wyznaczają okres referencyjny
f) ERD/ERS - względna zmiana sygnału e) w odniesieniu do okresu referencyjnego.
Klasycznie estymowanie ERD/ERS polega na wykonaniu następujących kroków (patrz rys.%i 2. ):
- filtrowanie pasmowe
- wyrównanie realizacji względem bodźca
- obliczanie mocy chwilowej (podniesienie do kwadratu wartości każdej próbki sygnału)
- uśrednienie mocy chwilowej po realizacjach
- wygładzenie przebiegu czasowego uśrednionej mocy chwilowej średnią biegnącą lub innym filtrem dolnoprzepustowym
- zastosowanie wzoru (%i 1) do wyliczenia względnych zmian mocy
Filtrowanie pasmowe dobrze jest wykonać przed pocięciem sygnału na realizacje aby zminimalizować efekty brzegowe filtra. Więcej na temat klasycznych metod liczenia można znaleźć w Pfurtscheller (1999), Pfurtscheller i Lopes da Silva (1999).
Rozszerzenie na przestrzeń czas-częstość
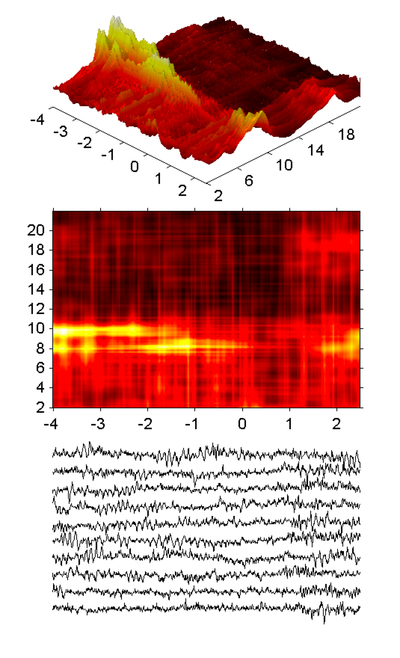
Klasyczna technika zaproponowana przez Pfurtscheller i Arnibar (1979) polega na uśrednianiu energii sygnałów przefiltrowanych w wybranym paśmie częstości. Wymaga ona wyboru reaktywnych pasm częstości, dających największe zmiany mocy. Pasm takich zwykle poszukiwano metodą prób i błędów. Pełen obraz zmian gęstości energii w przestrzeni czas - częstość można uzyskać uśredniając czasowo - częstościowe estymaty gęstości energii, obliczone dla każdego powtórzenia osobno. Najczęściej stosowanymi estymatorami są: spektrogram (krótkoczasowa transformata Fouriera- STFT) (Makeig, 1993) lub ciągłą transformata falkowa (CWT) (Tallon-Baudry et al., 1996). W sytuacjach gdy istotna jest wysoka rozdzielczość czasowo - częstotliwościowa stosowane jest dopasowanie kroczące (MP) (Durka et al., 2001) (rys. 3). Następnie dla każdego binu częstości, obliczana jest miara ERD/ERS, przy pomocy wzoru (%i 1). W efekcie uzyskiwana jest mapa prezentująca ERD/ERS w przestrzeni czas - częstość (rys. 3 środkowy panel).
Ocena istotności
Podobnie jak opisane w poprzednim rozdziale potencjały wywołane, ERD i ERS widoczne są jako efekty statystyczne w zapisach co najmniej kilkunastu powtórzeń. Klasyczne oraz czasowo - częstotliwościowe estymatory ERD/ERS obrazują zarówno istotne efekty jak i przypadkowe fluktuacje. Aby wyłowić istotne efekty musimy posłużyć się testami statystycznymi. Poniżej omówimy procedurę oceny istotności dla map czas - częstość (Durka et al., 2004; Zygierewicz et al., 2005). W przypadku klasycznym przebiega ona analogicznie.
- Każdą z map rozkładu gęstości energii dzielimy na elementy resele o rozmiarach [math] \Delta t [/math][math]\times[/math] [math]\Delta f [/math]. W ramach resela gęstość energii jest całkowana dając energię. Uzyskujemy w ten sposób podział przestrzeni na pasma częstości i na okienka czasowe.
- Następnie formułujemy zestaw hipotez. Dla każdego resela w analizowanym obszarze czas - częstość hipoteza zerowa [math]H_0[/math] stwierdza, że jego średnia energia jest równa średniej energii w reselach o tej samej częstości w okresie referencyjnym. Hipotezą alternatywną jest brak równości.
- Każdą z hipotez testuje się przy pomocy testu statystycznego (może to być test [math]t[/math], test permutacyjny lub repróbkowany, test nieparametryczny np. Wilcoxona (ten akurat testuje równość median). W wyniku, dla każdego resela dostajemy prawdopodobieństwo, że prawdziwa jest dla niego hipoteza [math]H_0[/math].
- Aby przyjąć bądź odrzucić hipotezę [math]H_0[/math] trzeba ustalić poziom istotności [math]\alpha[/math] biorąc pod uwagę fakt, że wykonaliśmy wiele testów. Odpowiedni poziom istotności można wyznaczyć stosując np. metodę FDR (False Discovery Rate) (Benjamini i Yekutieli, 2001).
- Ostatecznie w reselach dla których została odrzucona hipoteza [math]H_0[/math] prezentowany jest odpowiadający im fragment mapy ERD/ERS.
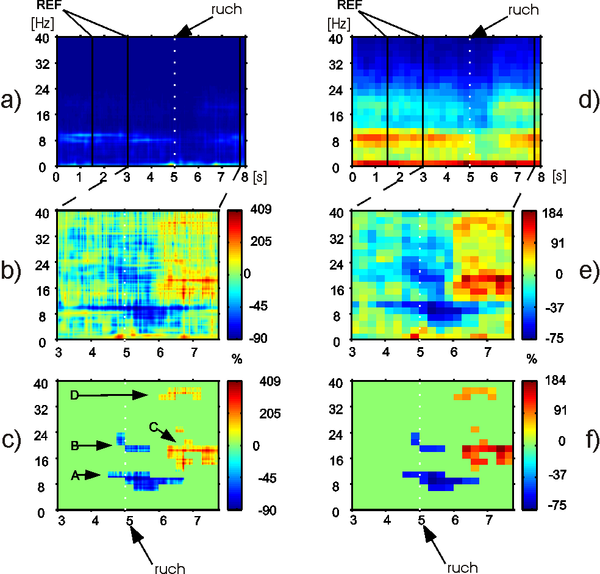
Procedura ta została zilustrowana na rys. 4.
Podstawowe wyniki eksperymentów
Poniżej wymienimy najczęściej obserwowane efekty ERD/ERS. Są one związane z poszczególnymi rytmami obserwowanymi w zapisach EEG i MEG. Bardzo ogólnie można powiedzieć, że rytm alfa jest interpretowany jako rytm spoczynkowy dużych populacji neuronów. Rytm beta wiązany jest z uwagą, zaś rytm gamma z aktywnym przetwarzaniem informacji.
- ERD w paśmie alfa
Spadek mocy w paśmie alfa w danej okolicy kory mózgowej interpretowany jest jako aktywacja znajdujących się tam neuronów, co powoduje ich wyjście ze stanu spoczynkowego. Blokowanie rytmu alfa często wywołane jest pojawieniem się bodźców w modalności, którą reprezentuje dany fragment kory (np. otwarcie oczu powoduje zanik rytmu alfa w korze wzrokowej, zaciśnięcie pięści blokuje fale o częstości alfa w korze czuciowej ręki). Spadek mocy w paśmie alfa często poprzedza zaangażowanie danego fragmentu kory w zamierzone działanie (np. ERD alfa w korze ruchowej ręki, zaczyna się już na 1 - 2 s przed wykonaniem zamierzonego ruchu tą ręką - rys 4c) struktura A).
- Efekt centrum-obrzeże
Efekt ten polega na wystąpieniu ERD w paśmie alfa w pewnym miejscu kory i jednoczesnym ERS w paśmie alfa w sąsiednich obszarach związanych z inną modalnością bądź kończyną (np. przy ruchu ręką obserwujemy ERD alfa w obszarze ręki i ERS alfa w obszarze nogi)
- ERD w paśmie beta
Efekt ten polega na spadku mocy w paśmie beta w obszarze kory mózgowej odpowiadającej modalności, na której skupiona jest uwaga, np. rys. 4c) struktura B.
- Odrzut ERS w paśmie beta
Efekt ten polega na przejściowym wzroście mocy powyżej poziomu z okresu referencyjnego, następujący po zakończeniu działania, któremu towarzyszył ERD w paśmie beta, np. rys 4c) struktura C.
- ERS w paśmie gamma
Efekt ten polegający na zwiększeniu mocy w paśmie gamma powyżej poziomu z okresu referencyjnego. Efekt ten obserwowany jest w niektórych eksperymentach EEG i w wielu eksperymentach z wykorzystaniem ECoG (elektrod umieszczonych bezpośrednio na korze) w trakcie gdy w danym fragmencie kory zachodzi przetwarzanie informacji. W EEG, gamma ERS zazwyczaj występuje w niskim paśmie około 40 Hz, natomiast w ECoG widoczne jest szerokopasmowe ERS gamma nawet w paśmie 40 - 120 Hz.
Literatura
Benjamini, Y., Yekutieli, Y. The control of the false discovery rate under dependency. Ann Stat 29: 1165–1188, 2001.
Durka, P.J. Matching Pursuit, Scholarpedia, p. 20910, 2007a [2]
Durka, P. J. Matching Pursuit and Unification in EEG analysis. Engineering in Medicine and Biology. Artech House, 2007b. ISBN 978-1-58053-304-1.
Durka, P. J., Ircha, D., Neuper, C., Pfurtscheller, G. Time-frequency microstructure of event-related desynchronization and synchronization. Med Biol Eng Comput 39(3): 315–321, 2001.
Durka, P.J., Zygierewicz, J., Klekowicz, H., Ginter, J., Blinowska, K. On the statistical significance of event-related EEG desynchronization and synchronization in the time-frequency plane. IEEE TransBiomed Eng 51: 1167–1175, 2004.
Makeig, S. Auditory event-related dynamics of the EEG spectrum and effects of exposure to tones. Electroencephalogr Clin Neurophysiol 86: 283–293, 1993.
Pfurtscheller, G. Quantification of ERD and ERS in the time domain. W Pfurtscheller, G., Lopes da Silva, F. H. (Edytorzy), Event-related desynchronization. Vol. 6. Elsevier, 89–105, 1999.
Pfurtscheller, G., Arnibar, A.Evaluation of event-related desynchronization(ERD) preceding and following voluntary self-paced movements. Electroencephalogr Clin Neurophysiol 46: 128–146, 1979.
Pfurtscheller, G., Lopes da Silva, F. H. Event-related EEG/MEG synchronization and desynchronization: basic principles. Clinical Neurophysiology 110: 1842–1857, 1999.
Tallon-Baudry, C., Bertrand, O., Delpuech, C., Pernier, J. Stimulus specificity of phase-locked and non-phase-locked 40Hz visual responses in human. Journal of Neuroscience 16(13): 4240–4249, 1996.
Zygierewicz, J., Durka, P., Klekowicz, H., Crone, N., Franaszczuk, P. Computationally efficient approaches to calculating significant ERD/ERS changes in the time-frequency plane. J Neurosci Methods 145(1–2): 267–276, 2005.
Problem odwrotny w elektro- i magnetoencefalografii
Jednym z najważniejszych i jednocześnie najtrudniejszych problemów elektroencefalografii (oraz MEG) jest lokalizacja przestrzenna źródeł aktywności rejestrowanej na zewnątrz czaszki, czyli rozwiązanie tzw. problemu odwrotnego EEG/MEG. Nawet przyjmując drastycznie uproszczony model źródeł jako dipoli prądowych, umieszczonych w jednorodnym przestrzennie przewodniku o kształcie idealnej kuli, stajemy przed problemem nie mającym jednoznacznego rozwiązania: istnieje nieskończenie wiele różnych konfiguracji prądów wewnątrz kuli, generujących dokładnie ten sam rozkład potencjałów na jej powierzchni -- co udowodnił von Helmholz już w roku 1853. Inaczej mówiąc, rozwiązania problemów odwrotnych są niejednoznaczne. Dlatego uzyskane tą drogą przestrzenne rozkłady źródeł aktywności są -- mimo pozornego podobieństwa -- czymś zupełnie innym niż obrazy uzyskiwane z tomografii komputerowej czy jądrowego rezonansu magnetycznego. W przypadku tych ostatnich, obraz trójwymiarowy rekonstruujemy z przekrojów o rozdzielczości znanej bezpośrednio z natury zjawisk fizycznych wykorzystywanych w procesie obrazowania. W przypadku rozwiązań odwrotnych EEG/MEG sytuacja jest niejako odwrócona: najpierw wybieramy zestaw kryteriów spośród wspomnianych w skrócie w dalszej części rozdziału, po czym na jego podstawie wybieramy jeden z możliwych rozkładów przestrzennych prądów, który na koniec możemy ew. wizualizować w postaci przekrojów. Dlatego nie powinno się używać w odniesieniu do rozwiązań problemu odwrotnego terminu tomografia.
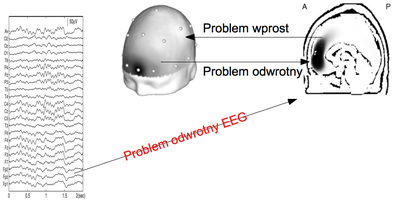
Pierwszym krokiem na drodze do rozwiązania problemu odwrotnego jest tzw. problem wprost, polegający na obliczeniu rozkładu potencjałów mierzonych na powierzchni głowy przy założeniu znanego rozkładu gęstości prądu wewnątrz mózgu. Należy jednak pamiętać, że:
- pola przenoszą się przez mózg, płyn owodniowy, czaszkę i skórę, mające różne przewodnictwa elektryczne. Przestrzenny kształt tych struktur anatomicznych jest różny dla każdego człowieka.
- nawet w/w ośrodki nie są jednorodne; szczególnie mózg, ze względu na obecność neuronów, wykazuje dużą anizotropowość przewodnictwa, czyli niejednorodność, zależnie od kierunku.
Zwykle przyjmuje się podział przestrzenny mózgu na elementy objętości zwane wokselami, od ang. volume element (analogicznie do piksela od picture element). W każdym wokselu przyjmujemy stałą wartość i kierunek gęstości prądu. Jeśli wartości te dla każdego woksela ułożymy w wektor [math]j[/math] o wymiarze trzykrotnie większym niż ilość wokseli [math]{N}_{v}[/math] (dla każdego woksela kierunek i wartość prądu określają trzy współrzędne przestrzenne), a potencjały mierzone na elektrodach umieścimy w wektorze [math]a[/math] o wymiarze [math]{n}_{e}[/math] równym liczbie czujników (elektrod), to propagację pola z każdego woksela do każdego czujnika opisywać będzie tzw. macierz przejścia (lead field) [math]\mathrm{K}[/math] o wymiarach [math]3 {N}_{v}[/math] na [math]{N}_{e}[/math]. Po uwzględnieniu nie objętego modelem szumu [math]e[/math], problem wprost przyjmuje postać z równania (Equation 2)
Macierz [math]\mathrm{K}[/math] znajdujemy rozwiązując równania Maxwella w przybliżeniu niskich częstości z więzami wyznaczonymi przez granice ośrodków. Najczęściej były one przybliżane modelem trzech koncentrycznych sfer, ale coraz częściej stosuje się np. metodę elementów skończonych dla obliczenia propagacji dla konkretnego mózgu, którego kształty znamy z segmentacji i trójwymiarowej rekonstrukcji obrazów MRI. W każdym przypadku informacje morfologiczne wykorzystuje się dla ograniczenia przestrzeni rozwiązań do fizjologicznie możliwych lokacji źródeł (np. kora mózgowa i hipokamp). W braku MRI dla danego pacjenta wykorzystuje się często dane z Atlasu Mózgu Człowieka (Talairach i Turnoux 1988).
Opisane powyżej problemy ze znalezieniem macierzy [math]\mathrm{K}[/math], czyli rozwiązaniem problemu wprost, to dopiero wstęp do rozwiązania problemu odwrotnego. Gęstości prądów [math]j[/math] dla wszystkich wokseli z powyższego równania wyznaczane są drogą minimalizacji szumu [math]e[/math]. Jednak choćby z faktu, że [math]{N}_{v} \gt \gt {N}_{e}[/math], widać konieczność przyjęcia dodatkowych więzów, takich jak np. jednoczesna minimalizacja normy rozwiązania (minimum energii) czy laplasjanu (maksymalna gładkość przestrzenna). Są to tzw. rozwiązania rozproszone (distributed solutions). W uzasadnionych przypadkach można też szukać rozwiązań w postaci z góry ustalonej liczby dipoli -- wtedy optymalizacji podlegać będą ich pozycje, kierunki i natężenia. Przegląd znanych rozwiązań znaleźć można w Scholarpedii (Ramirez i Makeig 2008).
Na koniec należy przypomnieć, że punktem wyjścia dla praktycznych rozwiązań problemu odwrotnego EEG nie są rozkłady potencjału, ale wielozmienne szeregi czasowe mierzone na każdej z elektrod (rys. 5). Można szukać rozwiązań dla każdego punktu w czasie z osobna, ale takie dane wejściowe będą obciążone dużym szumem, który szczególnie źle wpływa na rozwiązania odwrotne. Dlatego zwykle stosujemy przetwarzanie wstępne dla wyodrębnienia z danych aktywności związanych z badanym zjawiskiem, jak np. opisane rozdziale Metody analizy sygnałów EEG - analiza w dziedzinie czasu [3] uśrednianie potencjałów wywołanych. Duże nadzieje na poprawę jakości rozwiązań odwrotnych EEG/MEG daje czułość i selektywność adaptacyjnych przybliżeń czas-częstość (Durka 2007a, b; Durka et al., 2005).
Literatura
Durka, P.J. Matching Pursuit, Scholarpedia, p. 20910, 2007a [4]
Durka, P. J. Matching Pursuit and Unification in EEG analysis. Engineering in Medicine and Biology. Artech House, 2007b. ISBN 978-1-58053-304-1.
Durka, P. J., Matysiak, A., Montes, E. M., Valdes-Sosa P. i Blinowska, K. J. Multichannel matching pursuit and EEG inverse solutions. Journal of Neuroscience Methods, 148(1):49-59, 2005.
Ramírez R. R. i Makeig, S. Source localization, Scholarpedia, 2008 [http:www.scholarpedia.org/article/source_localization]
Talairach J. i Tournoux P. Co-Planar Stereotaxic Atlas of the Human Brain. Stuttgart, 1988.
Oprogramowanie do analizy danych EEG i MEG
Jako program do analizy danych EEG/MEG rozumiemy program implementujący przynajmniej część z metod analizy omówionych w poprzednim i bieżącym rozdziale. Pewną funkcjonalność w tym zakresie posiadają programy dostarczane przez producentów sprzętu rejesrującego czynność EEG/MEG. Każdy z nich ma przynajmniej możliwość wyświetlania sygnałów, bardzo często oznaczania interesujących fragmentów danych lub artefaktów, filtrowania w zadanych pasmach częstości, czasem możliwe jest wykonywanie analizy spektralnej dla zaznaczonego fragmentu danych.
Bardziej zaawansowane analizy prowadzi się zwykle w dedykowanych do tego programach. Poniżej krótko omówimy najbardziej popularne obecnie pakiety. Omówiony jest stan tych pakietów w czerwcu 2009. Dziedzina analizy sygnałów EEG i MEG rozwija się obecnie bardzo dynamicznie więc aktualne informację na temat każdego ze wspomnianych poniżej pakietów należy szukać na podanych stronach internetowych.
Pakiety otwarte (Open Source, GPL)
Obecnie dominują trzy pakiety. Wszystkie są toolboxami działającymi w środowisku Matlab. Każdy wyrósł z nieco odmiennych korzeni i stąd cechuje go pewna specyfika podejścia do problemów analizy, ale w chwili obecnej oferują one podobną funkcjonalność i zarówno dzięki wspólnej platformie jak i wysiłkom tworzących je ludzi możliwa jest mniej lub bardziej łatwa integracja funkcji z różnych toolboxów. Ponieważ pakiety te są wykonywane w Matlabie mają zaletę przenośności między różnymi systemami operacyjnymi, na których działa Matlab tzn. Linux, Unix, Windows i Mac OS X.
Fieldtrip
Fieldtrip jest typowym toolboxem tzn. nie posiada on własnego interface'u. W związku z tym wymaga on znajomości programowania w Matlabie. Dostarcza natomiast wielu funkcji służących do analiz czasowych i spektralnych sygnałów EEG/MEG. Jego specjalnością są implementacje metod rozwiązywania problemów wprost i odwrotnych i ich wizualizacja. Z funkcji dostępnych w toolboxie łatwo można składać skrypty do potokowego przetwarzania danych i lokalizacji źródeł.
Więcej informacji na stronie: http://fieldtrip.fcdonders.nl/
EEGLAB
EEGLAB jest interaktywnym toolboxem matlabowym do przetwarzania zarówno ciągłych jak i związanych z bodźcami danych EEG i MEG. Wyrósł jako narzędzie do analizy EEG na pozimie sensorów. Dostarcza on możliwość analizy składowych niezależnych (ICA), analiz czasowo-częstotliwościowych i wiele narzędzi do wizualizacji danych i wyników. Dzięki współpracy z toolboxem Fieldtrip możliwa jest lokalizacja źródeł czynności EEG i MEG.
EEGLAB ma dość przejrzysty interfejs użytkownika, tak że większość standardowych procedur analizy danych można "wyklikać". Dodatkowo tworzona jest historia wywoływanych funkcji. Ułatwia ona pisanie skryptów do obliczeń nieinteraktywnych. Mechanizm wtyczek (plug-inów) umożliwia rozbudowywanie funkcjonalności interfejcu EEGLABa.
Mocną stroną jest import wielu formatów danych. EEGLAB wspiera analizę zarówno pojedynczych datasetów jak i zbiorów danych agregowanych w tzw. studtset. Więcej informacji na stronie: http://sccn.ucsd.edu/eeglab/
SPM
SPM jest interaktywnym toolboxem. Ma bardzo rozbudowany interfejs. Ale wspiera też pisanie własych skryptów przetwarzania danych. Pakiet sięga korzeniami do analizy danych PET, MRI i fMRI. Aktualna wersja (SPM8) została rozbudowana o stosunkowo wygodną wersję do wczytywania i wstępnej obróbki szeregów czasowych. Bardzo mocną stroną SPM jest statystyczna obróbka wyników i bardzo dobra segmentacja obrazów MRI w oparciu o statysyki bayesowskie. Więcej szczegółów na stronie: http://www.fil.ion.ucl.ac.uk/spm/software/spm8/
Pakiety komercyjne
Curry
Curry oferuje pełną ścieżkę przetwarzania danych: od wstępnego przetwarzania danych, filtrowania sygnałów, przez analizy składowych głównych (PCA) lub składowych niezależnych (ICA) do lokalizacji źródeł aktywności elektrycznej.
Integruje informacje z różnych modalności obrazowych(MRI, fMRI, PET, SPECT and CT) do tworzenia indywidualnych modeli głowy metodą elementów granicznych BEM (Boundary Element Method).
Lokalizacja źródeł może być prowadzona przy użyciu indywidualnego modelu głowy, lub standardowych modeli głowy BEM lub modeli głowy opartych na elementach skończonych - Finite Element Method (FEM).
Metody lokalizacji źródeł to fitowanie dipoli, MUSIC, dla źródeł rozciągłych: beamforming, Lp norms, sLORETA, SWARM.
Możliwy jest eksport wyników do formatów Excel, MATLAB i SPM. Co ważne w zastosowaniach klinicznych produkt ma FDA Market Clearance for intended clinical applications.
Więcej szczegółów na stronie producenta: [5]
BESA
BESA jest programem nakierowanym na analizę źródeł czynności elektrycznej w mózgu. Można w niej przeprowadzić pełną ścieżkę od przeglądania i preprocesowania danych (filtrowanie, usuwanie artefaktów, uśrednianie) danych.
Do dyspozycji mamy standardowe modele głowy FEM.
Zaimplementowane metody lokalizacji źródeł dipolowych to multiple source probe scan (MSPS) for model validation i RAP-MUSIC z algorytmem genetycznym szukania optymalnego dopasowania.
Metody obrazowania źródeł rozciągłych: wieloźródłowy beamformer (multiple source beamformer (MSBF)), metody minimalizacji normy rozwiązania: LORETA, sLORETA, swLORETA, LAURA, SSLOFO.
Pakiet oferuje dodatkowo możliwości analiz czasowo - częstotliwościowych ERD/ERS oraz analizy koherencji źródeł.
Więcej informacji na stronie producenta: [6]