Fizyka III/Drgania wymuszone
Rozpatrujemy teraz układ w którym oprócz siły harmonicznej i siły oporu działa również siła (zwana siłą wymuszającą), która ma postać: [math]F_{wym}=F_0\cos(\Omega t)[/math]. Równanie ruchu jest wówczas następujące:
- [math]m\frac{\mathrm d^2 x}{\mathrm dt^2} +b\frac{\mathrm d x}{\mathrm dt}+kx = F_0\cos(\Omega t)[/math].
Po podzieleniu przez masę i wprowadzeniu oznaczenia [math]f_0=\frac{F_0}{m}[/math] otrzymujemy:
- [math]\ddot x +2\beta \dot x + \omega_0^2x = f_0\cos(\Omega t)[/math].
Jest to równanie niejednorodne, którego rozwiązaniem ogólnym jest suma rozwiązania równania jednorodnego i rozwiązania szczególnego równania niejednorodnego:
- [math]x(t)=x_j(t)+x_s(t)[/math].
Rozwiązanie równania jednorodnego dyskutowaliśmy w poprzednim rozdziale. Zajmijmy się na początek przypadkiem, gdy nie ma siły oporu. Wówczas musimy rozwiązać równanie:
- [math]\ddot x + \omega_0^2x = f_0\cos(\Omega t)[/math].
Rozwiązanie jednorodne możemy zapisać:
- [math]x_j(t)=C_1\cos(\omega_0t)+C_2\sin(\omega t)[/math].
Rozwiązanie szczególne szukamy korzystając z metody uzmiennia stałych:
- [math]x_s(t)=C_1(t)\cos(\omega_0t)+C_2(t)\sin(\omega t)[/math]
gdzie:
- [math]C_1(t) = -\frac 1 {m\omega_0}\int_0^tF(\tau)\sin(\omega_0\tau)\mathrm d\tau +A_1[/math]
- [math]C_2(t) = -\frac 1 {m\omega_0}\int_0^tF(\tau)\cos(\omega_0\tau)\mathrm d\tau +A_2[/math].
Ostatecznie uwzględniając warunki początkowe: [math]x(t=0)=x_0\ \mathrm{i}\ v(t=0)=v_0[/math] otrzymujemy rozwiązanie:
- [math]x(t)=\left(x_0-\frac{f_0}{\omega_0^2-\Omega^2}\right)\cos\omega_0t+\frac{v_0}{\omega_0}\sin\omega_0t+ \frac{f_0}{\omega_0^2-\Omega^2}\cos\Omega t[/math].
Zwróćmy uwagę, że jeśli [math]x_0[/math] i [math]v_0[/math] są równe zeru, to rozwiązanie jest następujące:
- [math]x(t)=\frac{f_0}{\omega_0^2-\Omega^2}\left(\cos\Omega t -\cos\omega_0t\right)=-\frac{f_0}{\omega_0^2-\Omega^2}\sin\frac{\Omega-\omega_0}{2}t\sin\frac{\Omega+\omega_0}{2}t[/math].
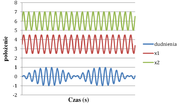
Jeśli częstość kołowa siły wymuszającej [math]\Omega[/math] jest bliska częstości drgań swobodnych układu [math]\omega_0[/math] to rozwiązanie jest złożeniem drgań o dwóch częstościach, częstości bliskiej [math]\omega[/math] oraz częstości bardzo małej [math]\frac{\Omega-\omega_0}{2}[/math]. Drgania o małej częstości nazywamy dudnieniami. Postać drgań pokazano na rysunku Figure 1.
Dla częstości siły wymuszającej [math]\Omega=\omega_0[/math] występuje tzw. rezonans. Amplituda drgań rośnie do nieskończoności, co możemy łatwo zauważyć:
- [math]x(t)\longrightarrow_{\Omega\rightarrow \omega_0} \frac{2f_0\cos\left(\frac{\Omega-\omega_0}{2}t\right)\frac 1 2 t}{2\Omega}\sin\left(\frac{\Omega+\omega_0}{2}t\right)\longrightarrow_{\Omega\rightarrow \omega_0}\frac{F_0t}{2m\Omega}\sin\omega_0t[/math].
W tym przypadku nawet jeśli amplituda siły wymuszającej [math]F_0[/math] jest bardzo mała, to i tak po dostatecznie długim czasie amplituda drgań będzie ogromna. Dlatego inżynierowie projektujący urządzenia, mosty, samoloty, etc. muszą uwzględniać zjawisko rezonansu w planowanych konstrukcjach.
Powszechnie wiadomo, że żołnierze przechodząc przez most nie maszerują “równym” krokiem, żeby nie wzbudzić drgań. Bardzo znany jest przypadek mostu Tacoma Bridge w USA, który wzbudzony do drgań przez wiejący wiatr zawalił się w 1943r w 4 miesiące i sześć dni po jego otwarciu. Częstotliwość rezonansowa wynosiła 0.2 Hz.
Rozpatrywany wyżej przykład jest “wyidealizowany”. W rzeczywistych układach zwykle działa siła oporu. Wracamy więc do przypadku ogólnego, tj. oscylatora harmonicznego wymuszonego z siłą tłumiącą. Skupmy uwagę na przypadku słabego tłumienia, a więc gdy rozwiązanie jednorodne jest postaci: [math]x_j(t)=A_0e^{-\beta t}\cos(\omega t +\Phi)[/math]. Rozwiązania szczególnego równania niejednorodnego będziemy poszukiwać, używając liczb zespolonych, tj. postulując rozwiązanie w formie: [math]z=Ae^{i\Omega t}[/math]. Rozwiązanie rzeczywiste (“prawdziwe”) otrzymamy biorąc część rzeczywistą z, tzn. [math]x=\mathrm{Re}(z)[/math]. Równanie ruchu w postaci zespolonej jest postaci:
- [math]\ddot z +2\beta\dot z+\omega_0^2z =\hat{f}[/math],
gdzie: [math]\hat f = f_0e^{i\Omega t}[/math]. Podstawiając postulowane rozwiązanie do równania, po prostych przekształceniach otrzymujemy rozwiązanie szczególne:
- [math]x_s= \frac{f_0}{\sqrt{(\omega_0^2-\Omega^2)+4\beta^2\Omega^2}}\cos(\Omega t +\Phi)[/math]
gdzie: [math]\tg\Phi = -\frac{2\beta\Omega}{\omega_0^2-\Omega^2}[/math]. Widzimy, że rozwiązanie szczególne odpowiada drganiom układu z częstością siły wymuszającej. Ruch jest jednak przesunięty w fazie względem tej siły. Czasami rozwiązanie szczególne przedstawiane jest w następującym zapisie:
- [math]x_s=\frac{f_0(\omega_0^2-\Omega^2)}{(\omega_0^2-\Omega^2)^2+4\beta^2\Omega^2}\cos\Omega t +\frac{2\beta\Omega f_0}{(\omega_0^2-\Omega^2)^2+4\beta^2\Omega^2}\sin(\Omega t)[/math].
Stała przed cosinusem nosi nazwę amplitudy elastycznej, natomiast stała przed sinusem amplitudy absorpcyjnej. Pełne rozwiązanie rozpatrywanego problemu jest następujące:
- [math]x=A_0e^{-\beta t}\cos(\omega t +\phi) +A\cos(\Omega t +\Phi)[/math]
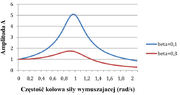
gdzie amplituda: [math]A=\frac{f_0}{\sqrt{(\omega_0^2-\Omega^2)^2+4\beta^2\Omega^2}}[/math]. Zwróćmy uwagę, że pierwszy składnik rozwiązania zanika z czasem. Po dostatecznie długim czasie składnik ten można pominąć i w rozwiązaniu ogólnym pozostaje tylko rozwiązanie szczególne. Mówimy, że w takim przypadku układ osiąga stan stacjonarny, a rozwiązanie opisujące ten stan nazywamy rozwiązaniem stacjonarnym. Amplituda A zależy od współczynnika tłumiącego [math]\beta[/math] oraz częstości siły wymuszającej [math]\Omega[/math]. Łatwo można policzyć, że amplituda osiąga maksimum dla częstości siły wymuszającej: [math]\Omega_r=\sqrt{\omega_0^2-2\beta^2}[/math]. Im współczynnik tłumienia większy tym amplituda mniejsza, a jej maksimum bardziej przesunięte w stronę mniejszych częstości względem [math]\omega_0[/math]
Prędkość wymuszonego oscylatora harmonicznego tłumionego z kolei opisana jest wzorem:
- [math]\dot x = -A\Omega \sin(\Omega t+\Phi)[/math].
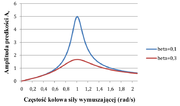
Łatwo możemy policzyć, że amplituda prędkości osiąga maksymalną wartość dla częstości siły wymuszającej: . W tym przypadku częstość rezonansowa nie zależy od współczynnika tłumienia. Na rysunku Figure 2 i Figure 3 pokazano zależność amplitudy położenia i prędkości od częstości siły wymuszającej.
Dokonajmy teraz analizy mocy dostarczanej przez siłę wymuszającą do układu dla stanu stacjonarnego. Moc ta zdefiniowana jest następująco:[math]P_{wym}=F_{wym}\cdot x[/math]. Podstawiając do tego wzoru rozwiązanie i licząc średnią po okresie drgań otrzymujemy wyrażenie:
- [math]\langle P_{wym}\rangle = \frac{F_0^2}{2m}\frac{2\beta\Omega^2}{4\beta^2\Omega^2+(\omega_0^2-\Omega^2)^2}[/math]
W analogiczny sposób możemy policzyć średnią moc traconą przez układ w związku z występowaniem siły oporu [math]\left(P_{op}(t)=\frac{\mathrm d E}{\mathrm dt}=\frac{F_t\mathrm dx}{\mathrm dt}=-b\frac{\mathrm dx}{\mathrm dt} \frac{\mathrm dx}{\mathrm dt}=-2\beta m \left(\frac{\mathrm dx}{\mathrm dt}\right)^2\right)[/math]:
- [math]\langle P_{op}(t) \rangle = -\frac 1 2 \frac{F_0^2}{m}\frac{2\beta\Omega^2}{4\beta^2\Omega^2+(\omega_0^2-\Omega^2)^2}[/math]
Otrzymaliśmy wyrażenie identyczne jak na średnią moc dostarczaną do układu, ale ze znakiem ujemnym. Oznacza to, ze w stanie stacjonarnym średnia moc układu (suma mocy dostarczanej do układu przez siłę wymuszającą i mocy traconej przez układ) wynosi zero, a więc średnia energia układu jest stała.
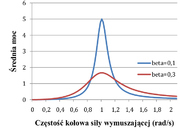
Zależność średniej mocy dostarczanej do układu przez siłę wymuszającą pokazano na rysunku Figure 4. Widzimy, że rezonans mocy (maksymalna wartość) występuje dla częstości siły wymuszającej: [math]\Omega_r=\omega_0[/math].
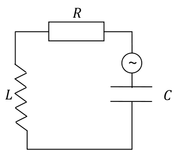
Na koniec rozważań dotyczących oscylatora wymuszonego dodajmy, że dla obwodów elektrycznych składających się ze zmiennego źródła napięcia [math]U(t)=U_0\cos\Omega t[/math] oraz opornika o oporze R, cewki o indukcyjności L i kondensatora o pojemności C połączonych szeregowo (patrz rysunek Figure 5) otrzymujemy analogiczne rozwiązania na ładunek na kondensatorze, Q oraz prąd płynący w obwodzie, I jak rozpatrywane wyżej rozwiązania na położenie i prędkość:
- [math]Q=A\cos(\Omega t+\Phi)\;[/math]
- [math]I=\dot Q = -A\Omega \sin(\Omega t+\Phi)[/math]
gdzie: [math]A=\frac{U_0}{\sqrt{(\Omega L-\frac 1 {\Omega}{C})^2+R^2}}[/math], [math]\Phi =\mathrm{arctg}\frac{-\frac{R}{L}\Omega}{\frac 1 {LC}-\Omega^2}[/math].