Fizyka III/Składanie drgań harmonicznych

Wstęp

Ze składaniem drgań harmonicznych zetknęliśmy się w poprzednim rozdziale, np. gdy mówiliśmy o oscylatorze wymuszonym. W przypadku braku tłumienia mieliśmy do czynienia ze zjawiskiem dudnień, natomiast gdy występuje siła oporu rozwiązanie jest postaci: [math]x(t) = Ae^{-\beta t }\cos(\omega t +\phi)+A\cos(\Omega t +\Phi)[/math]. Jak widzimy na powyższym przykładzie obowiązuje zasada superpozycji: wychylenie z położenia równowagi jest sumą wychyleń wywołanych przez poszczególne czynniki osobno. Zasada ta wynika z liniowości związku miedzy wychyleniem a siłą (oscylator harmoniczny).

Przejdźmy teraz do składania drgań odbywających się wzdłuż osi prostopadłych. Załóżmy następujące drgania:

[math]x = a\cos\omega t[/math]

[math]y=b\cos(\omega t+\delta)[/math]

Oba drgania harmoniczne odbywają się z tą samą częstością, ale są przesunięte w fazie o [math]\delta[/math]. Po prostych przekształceniach otrzymujemy ogólne równanie elipsy:

[math]\frac{y^2}{b^2}+\frac{x^2}{a^2}-\frac{2xy}{ab}\cos\delta = \sin^2\delta[/math]

W zależności od wartości przesunięcia fazowego ruch odbywa się po prostej lub po elipsie, np. Jeśli [math]\delta = 0,\pm\pi,\pm 2\pi,\ldots[/math], to ruch opisany jest równaniem:

[math]\left(\frac y b\mp\frac x a \right)^2=0[/math],

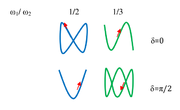
czyli równaniem prostej: [math]y=\mp \frac b a x[/math]. Z kolei jeśli [math]\delta = \pm \frac \pi 2[/math] to otrzymujemy równanie elipsy współosiowej z układem współrzędnych: [math]\frac{y^2}{b^2}+\frac{x^2}{a^2}=1[/math]. Ciekawą sytuację mamy gdy częstości składanych drgań harmonicznych są różne. W takim przypadku otrzymujemy tzw. Figury Lissajoux, których przykład pokazano na rysunku Figure 1. Jeśli spełniony jest warunek: [math]\frac{\omega_1}{\omega_2} = \frac k l[/math], gdzie k i l są liczbami naturalnymi to krzywe opisujące ruch są krzywymi zamkniętymi.

Przykłady figur Lissajoux dla różnych stosunków częstości oraz przesunięcia fazowego

W przypadku składania drgań harmonicznych niezwykle pomocne jest twierdzenie Fouriera. Mówi ono, że dowolne drgania periodyczne o okresie T opisane funkcją [math]x=f(t)=f(t+T)[/math] można rozłożyć na nieskończony zbieżny szereg drgań harmonicznych o częstotliwościach będących wielokrotnością częstotliwości podstawowej:

[math]f(t)=\Sigma_{n=0}^\infty[/math],

gdzie: [math]\omega = \frac{2\pi}{T}[/math]. Natomiast stałe w rozwinięciu wyznaczamy w oparciu o wzory:

[math]B_0=\frac 1 T \int_0^T f(t)dt[/math]

[math]A_m =\frac 2 T\int_0^Tf(t)\sin m\omega t\mathrm dt[/math]

[math]B_m = \frac 2 T\int_0^Tf(t)\cos m\omega t\mathrm dt[/math]

Dzięki temu twierdzeniu np. dowolną periodyczną siłę wymuszającą (źródło napięcia zmiennego w obwodzie elektrycznym) możemy przedstawić za pomocą składowych harmonicznych, a jak rozwiązywać problem harmonicznej siły wymuszającej nauczyliśmy się w poprzednim rozdziale.

Przykład

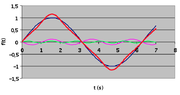
Na koniec przykład. Rozwińmy na szereg Fouriera funkcję w kształcie piły. Wynik rozwinięcia jest następujący:

Rozwinięcie funkcji “piła” na szereg Fouriera dla A=1 i [math]\omega=1[/math]

.

[math]f(t)=A\left(\frac{1}{1^2}\sin\omega t -\frac{1}{3^2}\sin3\omega t +\frac{1}{5^2}\sin5\omega t -\ldots\right)[/math]

Widzimy, że współczynniki stojące przy funkcjach sinus maleją ze wzrostem częstości. Na rysunku Figure 2 pokazano złożenie trzech pierwszych składników tego rozwinięcia. Ograniczenie tylko do tych wyrazów zupełnie dobrze odtwarza kształt funkcji, aczkolwiek w przypadku kształtów mających “ostre” kanty całkowite odtworzenie kształtu wymaga uwzględnienia praktyczne wszystkich składników rozwinięcia.