Fizyka III/Fale dźwiękowe
Fale dźwiękowe — wstęp
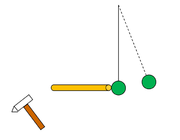
Falami dźwiękowymi nazywamy fale podłużne, które rozchodzą się w ośrodkach sprężystych. Ludzkie ucho rozpoznaje fale dźwiękowe o częstotliwości od około 20 Hz do około 20 kHz (zakres ten zależy od indywidualnych cech i może się trochę różnić dla konkretnego człowieka). Falę dźwiękową możemy wytworzyć uderzając np. młotkiem w cienki pręt metalowy tak jak to pokazano na rysunku Figure 1. Fala dźwiękowa rozchodząc się w pręcie zmienia lokalnie gęstość i naprężenia. Powstałe na końcu pręta odkształcenie powoduje „odskoczenie” piłeczki.
W przypadku struny, funkcja falowa opisywała wychylenie poszczególnych punktów struny z położenia równowagi. Co będzie opisywała funkcja falowa w przypadku fali dźwiękowej w cienkim pręcie?
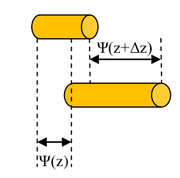
Wyobraźmy sobie mały kawałek (fragment) pręta w kształcie walca o długości [math]\Delta z[/math] i przekroju S (patrz rysunek Figure 2). W wyniku rozchodzenia się fali przesuną się denka walca, denko z lewej strony o [math]\Psi(z,t)[/math], natomiast denko z prawej strony o [math]\Psi(z+\delta z,t)[/math]. Jeśli [math]\Psi(z,t)= \Psi(z+\Delta z,t)[/math] to walec tylko się przesunie, bez zmiany długości. Jeśli [math]\Psi(z,t)\lt \Psi(z+\Delta z,t)[/math] to walec ulegnie rozciągnięciu, a w przypadku [math]\Psi(z,t)\gt \Psi(z+\Delta z,t)[/math] ściśnięciu. Przy zmianie długości walca na jego końce będzie działać siła wynikająca z prawa Hooke’a:
- [math]F = ES\frac{\Psi(z+\Delta z,t)-\Psi(z,t)}{\Delta z}\rightarrow_{\Delta z\rightarrow0}ES \frac{\partial\Psi}{\partial z}[/math]
gdzie parametr E jest modułem Younga. Uwzględniając siłę wypadkową działającą na walec (różnica sił działających na lewe i prawe denko) oraz masę walca: [math]m=\rho S \Delta z\;[/math] otrzymujemy równanie:
- [math]\frac{\partial^2 \Psi_z(z,t)}{\partial t^2}=\frac E\rho \frac{\partial^2 \Psi_z(z,t)}{\partial z^2}[/math]
Otrzymaliśmy podobnie jak dla struny klasyczne równanie falowe z prędkością rozchodzenia się fali dźwiękowej: [math]v=\sqrt{\frac E \rho}[/math].
Przykładowo, dla cienkiego ołowianego pręta korzystając z powyższego wzoru łatwo możemy wyliczyć prędkość:
- [math]E=\unit{1,6\cdot 10^{10}}{Pa},\ \rho=\unit{11,3\cdot 10^3}{\frac{kg}{m^3}}[/math]
stąd:
- [math]v=\sqrt{\frac E \rho}=\unit{1190}{\frac m s}[/math]
Przeprowadzane rozważania, w tym wyprowadzenie klasycznego równania falowego były oparte na prawie Hooke’a, a więc dotyczyły cienkich prętów. Okazuje się jednak, że postać klasycznego równania falowego dla fal jest taka sama dla dowolnych materiałów objętościowych (o dowolnych kształtach), musimy jedynie w równaniu zamienić moduł Younga na współczynnik sprężystości objętościowej nazywany również modułem ściśliwości, który jest oznaczany zwykle literą [math]B[/math]. Moduł ściśliwości jest zdefiniowany: [math]B=-\frac{\mathrm dp}{\frac{\mathrm dV}{V}}[/math], a równanie falowe ma postać:
- [math]\frac{\partial^2 \Psi_z(z,t)}{\partial t^2}=\frac B\rho \frac{\partial^2 \Psi_z(z,t)}{\partial z^2}[/math]
Prędkość rozchodzenia się fali wynosi zatem: [math]v=\sqrt{\frac B \rho}[/math]. Zwykle [math]B\gt E\;[/math], a więc fala dźwiękowa rozchodzi się szybciej w materiale objętościowym niż w cienkim pręcie. Poniżej zebrano przykładowe prędkości fali dźwiękowej w wybranych materiałach (objętościowych).
| Substancja | [math]\unit{v}{\left[\frac ms\right]}[/math] | Uwagi |
|---|---|---|
| Ciekły hel | 211 | 4 K |
| Rtęć | 1450 | 20° C |
| Woda | 1402 | 0° C |
| Woda | 1482 | 20° C |
| Woda | 1543 | 100° C |
| Aluminium | 6420 | fale podłużne |
| Miedź | 4700 | w materiałach |
| Ołów | 2160 | objętościowych |
| Stal | 5941 | niesk. rozciągł. |
| Pleksiglas | 2670 | 20° C |
Długość fali zależy od prędkości i częstotliwości [math]\lambda=\frac v f[/math]. Zmienia się więc gdy np. fala dźwiękowa przechodzi z jednego ośrodka do drugiego. Zwróćmy też uwagę, że zdolność rozdzielcza przyrządów akustycznych zależy od częstotliwości. Np. sonar, który jest używany do wykrywania podwodnych obiektów wysyła fale dźwiękowe o częstotliwości 262 Hz co odpowiada [math]\lambda=\unit{5,65}{m}[/math]. Fale odbite od podwodnych obiektów wracają do sonara. Sonar może więc wykrywać obiekty nie mniejsze niż długość fali a więc obiekty o rozmiarach co najmniej kilkumetrowych. Z kolei delfiny do wykrywania obiektów posługują się falami o długości [math]\lambda=\unit{1,48}{m}[/math] a więc mogą wykrywać mniejsze obiekty niż sonar, natomiast w badaniach lekarskich za pomocą techniki USG wykorzystującej fale dźwiękowe o częstotliwości 5 MHz (ultradźwięki) można wykrywać obiekty o rozmiarach: [math]\lambda=\unit{0,33}{m}[/math].
Przeprowadzając analogiczne rozważania jak wyżej dla gazów otrzymujemy identyczną postać klasycznego równania falowego. Możemy się zastanowić jakiej przemianie podlega gaz podczas rozchodzenia się w nim fali dźwiękowej, zakładając, że gaz jest idealny? Porównanie doświadczenia z wzorami teoretycznymi jednoznacznie wskazuje, że gaz podlega przemianie adiabatycznej. Wyprowadźmy zatem dla takiej przemiany wzór na prędkość rozchodzenia się fali. Dla przemiany adiabatycznej ciśnienie gazu wynosi: [math]p=\frac{p_0V_0^\chi}{V^\chi}[/math], gdzie wielkości z indeksem 0 odpowiadają ciśnieniu i objętości w stanie normalnym (gdy fala nie rozchodzi się w gazie) a [math]\chi=\frac{c_p}{c_V}[/math]. Dla tego przypadku moduł ściśliwości wynosi: [math]B=-V\frac{\mathrm dp}{\mathrm dV}=\chi p[/math].
Z drugiej strony dla gazu idealnego: [math]pV=nRT[/math], gdzie [math]n[/math] jest liczbą moli, [math]R[/math] stałą gazową a [math]T[/math] temperaturą. Po prostych przekształceniach otrzymujemy: [math]\frac p\rho=\frac nm RT = \frac{RT}{M}[/math], gdzie [math]\rho[/math] jest gęstością gazu, [math]m[/math] masą a [math]M[/math] masą molową. Stąd łącząc powyższe wzory otrzymujemy wyrażenie na prędkość fali dźwiękowej w gazie:
- [math]v=\sqrt{\frac{\chi RT}M}\propto \sqrt T[/math].
Prędkość jest więc proporcjonalna do pierwiastka z temperatury. Korzystając z tego wzoru możemy łatwo policzyć prędkość dźwięku w powietrzu uwzględniając dane:
- [math]T=\unit{20}{^oC}[/math]
- [math]M=\unit{28,8\cdot 10^{-3}}{\frac{kg}{mol}}[/math]
- [math]R=\unit{8,314472}{\frac J{mol K}}[/math]
- [math]\chi=1,4\;[/math]
stąd:
- [math]v=\sqrt{\frac{\chi RT}M}=\unit{344}{\frac ms}[/math]
Otrzymana wartość bardzo dobrze zgadza się z danymi doświadczalnymi. Zwróćmy uwagę, że gdyby podczas rozchodzenia się fali dźwiękowej gaz podlegał przemianie izotermicznej to wartość teoretyczna prędkości byłaby mniejsza około 1.18 razy czyli o około 18%.
Poniżej pokazano prędkość dźwięku dla wybranych gazów.
| Substancja | [math]v[/math] [m/s] | Uwagi |
|---|---|---|
| Hel | 981 | 0° C, 1 atm |
| Azot | 336 | 0° C, 1 atm |
| Tlen | 313 | 0° C, 1 atm |
| Wodór | 1300 | 0° C, 1 atm |
| Powietrze | 331 | 0° C, 1 atm |
| Powietrze | 344 | 20° C, 1 atm |
Zwróćmy uwagę, że w przypadku fali rozchodzącej się w strunie funkcja falowa miała prosta interpretację, oznaczała bowiem wychylenie struny z położenia równowagi w danym punkcie z w chwili czasu [math]t[/math]. W przypadku fali podłużnej interpretacja funkcji falowej jest trudniejsza, wedle naszych rozważań oznacza bowiem przesuniecie hipotetycznego denka wydzielonego walca materiału. Łatwo jednak możemy przejść do innych wielkości fizycznych jak zmiana ciśnienia lub gęstości ośrodka w którym rozchodzi się fala. Ciśnienie wyraża się bowiem wzorem: [math]p=p_0-B\frac{\partial\Psi}{\partial z}[/math], natomiast gęstość (co łatwo można wyprowadzić): [math]\rho=\frac{\rho_0}{1+\frac{\partial\Psi}{\partial z}}\approx \rho_\left(1-\frac{\partial\Psi}{\partial z}\right)[/math]. Możemy zatem rozchodzenie się fali rozpatrywać jako rozchodzenie się zaburzenia ciśnienia lub gęstości: [math]\Delta p =p-p_0,\ \Delta\rho=\rho=\rho_0[/math]. Dla fali harmonicznej otrzymujemy wyrażenia:
- [math]\Psi(z,t)=A\cos(kz-\omega t)[/math]
- [math]\Delta p(z,t) =\delta p_0\sin(kz-\omega t)[/math]
- [math]\Delta \rho(z,t)=\delta \rho_0\sin(kz-\omega t)[/math]
Jako przykład zastosowania powyższych wzorów policzmy: ile wynosi amplituda A dla fali o częstotliwości 1 kHz, jeśli amplituda fluktuacji ciśnienia jest równa [math]\Delta p_0=\unit{4\cdot 10^{-2}}{Pa}[/math]?
Zgodnie z powyższymi wzorami: [math]\Delta p(z,t) =-B\frac{\partial\Psi}{\partial z}=BA k \sin(kz -\omega t) = BA \frac\omega v \sin(kz -\omega t)[/math] oraz: [math]B=\unit{1,42\cdot 10^5}{Pa},\ v=\unit{344}{\frac ms}[/math] a stąd:
- [math]A=\frac{\Delta p_0 v}{2\pi f B}=\unit{1,2\cdot 10^{-8}}{m}[/math]
Natężenie fali dźwiękowej, podobnie jak dla struny, zdefiniowane jest jako średnia moc dostarczana na jednostkę powierzchni. W przeciwieństwie jednak do struny fala dźwiękowa (w materiałach objętościowych) rozchodzi się izotropowo we wszystkich kierunkach, tj. [math]I=\frac{P_\mathrm{zrodla}}{4\pi r^2}[/math] gdzie r jest odległością od źródła. Dla fali harmonicznej [math]\Psi(z,t)=A\cos(kz-\omega t)[/math] moc drgającej warstwy powietrza (czy innego ośrodka sprężystego) wynosi: [math]P=\Delta p S\frac{\partial\Psi}{\partial t}=BA\frac \omega v S A\sin^2 (k-\omega t )=v\rho A^2 \omega^2 S\sin^2(kz-\omega t)[/math], a stąd moc średnia: [math]\langle P\rangle_\mathrm{sr}=\frac 1 2 \rho v SA^2\omega^2[/math] i natężenie fali dźwiękowej wynosi:
- [math]I=\frac 12 \rho v A^2 \omega^2 =\frac 12 ZA^2\omega^2[/math],
Z jest oporem falowym. Otrzymaliśmy więc identyczne wyrażenie jak dla struny. Wspominaliśmy jednak, że opis fali dźwiękowej wygodniej, bo bardziej „fizycznie” jest przedstawiać za pomocą zmiany ciśnienia. Dla fali harmonicznej związek ten łatwo wyprowadzamy:
- [math]\Delta p=BA\frac \omega v \sin(kz-\omega t) =\rho vA\omega \sin(kz-\omega t)=\rho v A\omega\sin(kz-\omega t)[/math], a stąd:
- [math]\langle \delta p^2\rangle = \langle \rho^2 v^2 A^2 \omega^2 \sin^2(kz-\omega t)\rangle = \frac 1 2 Z^2 A^2\omega^2[/math], czyli ostatecznie:
- [math]I=\frac{\Delta p^2_\mathrm{sr}}{Z}[/math].
W języku ciśnienia natężenie dźwięku jest średnią kwadratu fluktuacji ciśnienia związanej z rozchodzeniem się fali przez opór falowy. Jako przykład policzmy ile wynosi amplituda A oraz średnia wartość fluktuacji ciśnienia fali o częstotliwości 1 kHz dla natężenia odpowiadającego progowi słyszalności ludzkiego ucha? Próg słyszalności zdrowego ucha wynosi: [math]I_0=\unit{10^{-12}}{\frac{W}{m^2}}[/math].
Korzystając z danych:
- [math]f=\unit{1}{kHz}[/math]
- [math]\rho=\unit{1,2}{\frac{kg}{m^3}}[/math]
- [math]v=\unit{344}{\frac ms}[/math]
otrzymujemy:
- [math]A=\unit{0,24\cdot 10^{-10}}{m}[/math]
- [math]\sqrt{\Delta p_\mathrm{sr}^2}=\unit{2\cdot 10^{-5}}{Ps}[/math].
Wyliczone wartości są niezwykle małe. Świadczą też o tym jak znakomitym narządem zmysłu jest ludzkie ucho. Ucho jest jedynym narządem, które potrafi odbierać dźwięki o natężeniu różniącym się 1012 razy!!! Jest to możliwe dzięki temu, że wrażenie dźwiękowe odbierane przez człowieka jest proporcjonalne do logarytmu natężenia dźwięku (prawo Webera-Fechnera). Dlatego dla opisu tych wrażeń wprowadza się pojecie głośności dźwięku, które jest zdefiniowane:
- [math]\beta =10\log\frac I{I_0}[/math]
gdzie [math]I_0=\unit{10^{-12}}{\frac{W}{m^2}}[/math] jest wspominanym wyżej progiem słyszalności. Jednostką słyszalność jest decybel.
Poniżej zebrano przykładowe wartości natężenia dźwięku i odpowiadającą jej wartość głośności.
| Źródło | [math]\unit{\beta}{[dB]}[/math] | [math]\unit{I}{\left[\frac W{m^2}\right]}[/math] |
|---|---|---|
| Samolot wojskowy (30m) | 140 | 102 |
| Granica bólu | 120 | 1 |
| Pociąg | 90 | 10-2 |
| Głośny ruch uliczny | 70 | 10-5 |
| „Zwykła” rozmowa | 65 | 3,2x10-6 |
| Cichy samochód | 50 | 10-7 |
| Ciche radio w domu | 40 | 10-8 |
| Średni szept | 20 | 10-10 |
| Szelest liści | 10 | 10-11 |
| Próg słyszalności (1 kHz) | 0 | 10-12 |
Rozwiążmy następujący prosty problem: o ile zmieni się głośność, jeśli odległość źródła dźwięku od słuchacza wzrośnie dwa razy?
Korzystając ze znanych wzorów otrzymujemy:
- [math]\beta_2-\beta_2=10\left(\log_{10}\frac{I_2}{I_0}-log_{10}\frac{I_1}{I_0}\right)=10\log_{10}\frac{I_2}{I_1}[/math].
Ponieważ: [math]\frac{I_2}{I_1}=\frac{r_1^2}{r_2^2}=\frac 1 4[/math] to ostatecznie otrzymujemy: [math]\beta_2-\beta_2=10\log_{10}\frac 1 4=\unit{-6}{dB}[/math].
Efekt Dopplera
Z falami dźwiękowymi wiąże się pewien charakterystyczny efekt, odkryty już w wieku XIX przez Christiana Dopplera i który nosi nazwę od odkrywcy efektem Dopplera. Jest to efekt klasyczny, nieuwzględniający efektów relatywistycznych, związany z poruszaniem się źródła dźwięku lub obserwatora względem ośrodka sprężystego w którym rozchodzi się fala dźwiękowa.
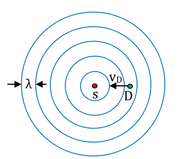
Załóżmy najpierw ze źródło dźwięku i obserwator są nieruchomi względem ośrodka sprężystego, tak jak na rysunku Figure 3.
Źródło emituje izotropowe fale o częstotliwości: [math]f_0[/math]. Częstotliwość odbierana przez obserwatora jest taka sama: [math]f=\frac{\frac{vt}{\lambda}}t[/math]. v jest prędkością fali, a [math]\lambda[/math] długością fali. Częstotliwość obserwator wyznacza w ten sposób, ze w określonym czasie t, liczy liczbę grzbietów fali. Gdy obserwator zbliża się do źródła z prędkością [math]v_D[/math] to liczba policzonych grzbietów rośnie, a więc i częstotliwość obserwowana przez obserwatora jest większa i wynosi: [math]f=\frac{\frac{vt+v_Dt}{\lambda}}t=f_0\frac{v+v_D}{v}[/math].
Analogicznie, jeśli obserwator oddala się od źródła o obserwuje częstotliwość wynosi: [math]f=\frac{\frac{vt-v_Dt}{\lambda}}t=f_0\frac{v-v_D}{v}[/math].
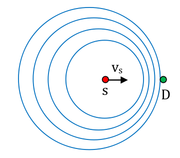
Inaczej wygląda sytuacja gdy obserwator jest nieruchomy a porusza się źródło z prędkością [math]v_S[/math]. Ruch źródła względem ośrodka powoduje, ze zmienia się długość fali dźwiękowej, a jej wartość zależy od kierunku, co pokazano na rysunku Figure 4.
Jeśli źródło zbliża się do obserwatora to obserwowana długość fali wynosi: [math]\lambda'=vT-v_ST[/math] (T jest okresem), a stąd częstotliwość obserwowana przez obserwatora:
- [math]f=\frac v\lambda =\frac{v}{vT-v_ST}=f_0\frac{v}{v-v_S}[/math].
Jeśli natomiast źródło oddala się od obserwatora, to analogiczne rozważania prowadzą do wyrażenia:
- [math]f=\frac v \lambda = \frac v{vT+v_ST}=f_0\frac{v}{v+v_S}[/math].
Możemy więc napisać ogólny wzór na wartość częstotliwości odbieranej przez obserwatora, dla przypadku gdy źródło lub/i obserwator poruszają się w kierunku do lub od obserwatora/źródła:
- [math]v_\pm = f_0\frac{v\pm v_D}{v\mp v_s}[/math].
Indeks plus odnosi się do sytuacji gdy źródło i obserwator zbliżają się do siebie, indeks minus, gdy się oddalają.
Jeśli natomiast kąt pomiędzy kierunkiem rozchodzenia się fali a kierunkiem prędkości obserwatora względem ośrodka wynosi [math]\phi[/math], a [math]\phi'[/math] jest kątem pomiędzy kierunkiem prędkości źródła, a kierunkiem od źródła do obserwatora to ogólny wzór na efekt Dopplera jest następujący:
- [math]f=f_0\frac{v-v_D\cos\phi}{v-v_S\cos\phi'}[/math].
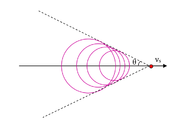
Zwróćmy uwagę, że źródło dźwięku może poruszać się z prędkością większą niż prędkość dźwięku, jak np. kula karabinowa czy samolot ponaddźwiękowy. W takim przypadku powstaje tzw. fala uderzeniowa, czyli front dużej fluktuacji ciśnienia wywołany nakładaniem się czuł fal dźwiękowych, co ilustruje rysunek Figure 5.
Połowa kąta rozwarcia powstałego stożka nosi nazwę kąta Macha. Zachodzi związek między katem Macha [math]\theta[/math] a prędkością dźwięku i źródła: [math]\sin\theta =\frac v{v_S}[/math].
Na koniec rozważań dotyczących fal dźwiękowych należy podkreślić, że podobnie jak dla fal w strunie, fale dźwiękowe mogą być biegnące lub stojące. Fale stojące są wytwarzane w instrumentach muzycznych, jak np. w trąbce czy organach. Dźwięki wytwarzane przez instrumenty muzyczne zwykle składają się nie z jednej częstotliwości ale kilku. Dlatego wrażenia słuchowe są różne od różnych instrumentów.