Pracownia EEG/EEG wlasnosci EEG spoczynkowego
Spis treści
Estymacja funkcji autokowariancji, autokorelacji i koherencji sygnału.
Wstęp
Z funkcjami tymi spotkaliśmy się już na zajęciach z analizy sygnałów.
Funkcja autokowariancji sygnału charakteryzuje liniową zależność wartości tego sygnału w danej określonej chwili czasu od wartości (tego samego sygnału) w innej chwili. W przypadku stacjonarnych procesów stochastycznych, przebieg tej funkcji nie zależy od czasu. Oznacza to, że obliczając funkcję autokorelacji sygnału pomiędzy chwilą czasu [math]x(t)[/math] i [math]x(t+\tau )[/math] otrzymamy tę samą wartość, jak dla przypadku obliczania funkcji autokorelacji pomiędzy momentami [math]x(t + T)[/math] i [math]x(t + T+\tau )[/math], gdzie [math]T[/math] to dowolny przedział czasu. Innymi słowy, funkcja autokorelacji procesu stacjonarnego zależy tylko od odstępu czasu pomiędzy próbkami [math]\tau[/math], dla którego jest wyznaczana, a nie od konkretnej chwili czasu. Odrębną klasę sygnałów stanowią procesy niestacjonarne, w przypadku których funkcja autokorelacji będzie zależeć od czasu [math]t[/math] w którym jest obliczana. Estymator funkcji autokowariancji uzyskuje się poprzez obliczanie iloczynów wartości sygnału [math]x[/math] w chwilach czasu [math]t[/math] czyli [math]x(t)[/math] i wartości sygnału [math]x[/math] w chwili czasu t+τ czyli [math]x(t+\tau)[/math] i uśredniając wartości iloczynów po czasie [math]T[/math]:
gdzie:
W przypadku sygnałów ciągłych estymację tę można zapisać w poniższy sposób:
natomiast dla sygnałów dyskretnych jako:
gdzie:
Funkcja autokowariancji może osiągać dowolne wartości, dlatego aby można było porównać przebieg tej funkcji np. pomiędzy dwoma sygnałami, wprowadzono wersję znormalizowaną tej funkcji - funkcję autokorelacji. Normalizacja ta wygląda następująco:
gdzie:
Wariancję sygnału ([math]\gamma (0)=\sigma ^2[/math]) można wyrazić przez funkcję autokowariancji dla przesunięcia [math]\tau =0[/math]. Wynika z tego, że funkcja korelacji przyjmuje wartości z zakresu [math][-1, \, 1][/math]. Ostatecznie estymator funkcji autokorelacji można zapisać jak poniżej:
Funkcję autokorelacji estymuje się w celu określenia, w jakim stopniu wartości sygnału w danej chwili czasu wpływają na wartości sygnału w kolejnych chwilach czasu. Ma to kluczowe znaczenie przy rozpoznawaniu rodzaju procesów fizycznych odpowiedzialnego za generowanie sygnału. Funkcja ta zawsze mam maksimum dla przesunięcia [math]\tau =0[/math].
Cechą charakterystyczną funkcji autokorelacji jest to, iż w przypadku sygnałów harmonicznych, przebieg funkcji ma charakter okresowy, z okresem takim samym o okres badanego sygnału. W przypadku szumu, funkcja autokorelacji ma kształt funkcji delta Diraca.
Polecenie:
Zaimplementuj funkcję do obliczania funkcji korelacji zgodnie ze wzorem (4). Funkcja powinna przyjmować dwa wektory i maksymalne przesunięcie wzajemne tych wektorów, natomiast zwracać powinna wektor zawierający funkcję autokorelacji. Wywołanie przykładowe:
a = np.array([1,2,3])
print koreluj(a,a,2)
powinno dać wynik:
[-0.5 0. 1. 0. -0.5]
Zadanie 1: Funkcje autokowariancji i autokorelacji
W tym zadaniu posłużymy się sygnałami zarejestrowanymi w punkcie 4. poprzedniego ćwiczenia. Zaobserwuj, na którym kanale rytm alfa osiąga najwyższą wartość. Następnie zaimplementuj w Pythonie następujące kroki:
- Wczytaj dane z wybranego kanału.
- Oblicz funkcję autokorelacji dla sygnału zarejestrowanego w warunkach, gdy osoba badana siedziała z otwartymi oczami. Narysuj autokorelogram, to jest wykres wartości funkcji autokorelacji względem przesunięcia [math]\tau [/math]. Oś [math]\tau [/math] wyskaluj w sekundach.
- Powtórz krok 2, tym razem za sygnału zebranego w warunkach czuwania z zamkniętymi oczami.
- Porównaj autokorelogramy.
Związek autokorelacji z widmem sygnału
Wstęp
Zgodnie z twierdzeniem Chinczyna, z którym zapoznaliśmy się na wykładzie z Analizy Sygnałów, widmową gęstość mocy sygnału można policzyć jako transformatę Fouriera funkcji autokowariancji:
gdzie:
- [math]f[/math] — częstość
- [math]S(f)[/math] — gęstość widmowa mocy
Polecenie 1
Zaimplementuj funkcję obliczającą transformatę Fouriera dyskretyzując wzór (9) dla zadanego wektora częstości f i zadanej częstości próbkowania sygnału (tutaj 10.0):
Wywołanie przykładowe:
t= np.arange(0,1,0.1)
x = np.sin(2*np.pi*2*t)
f = np.arange(-5,5,1)
X,f = fourier(x,f,10.0)
print X
Powinno dać:
[ 3.15975012e-16 +5.19678720e-16j 1.05325004e-16 +3.51083347e-16j -4.56408351e-16 -2.10650008e-16j 4.91516686e-16 +1.58113883e+00j -1.40433339e-16 -7.02166694e-17j 0.00000000e+00 +0.00000000e+00j -1.40433339e-16 +7.02166694e-17j 4.91516686e-16 -1.58113883e+00j -4.56408351e-16 +2.10650008e-16j 1.05325004e-16 -3.51083347e-16j]
Natomiast wywołanie:
t= np.arange(0,1,0.1)
x = np.sin(2*np.pi*2*t)
f = np.arange(-5,5,0.01)
X = fourier(x,f,10.0)
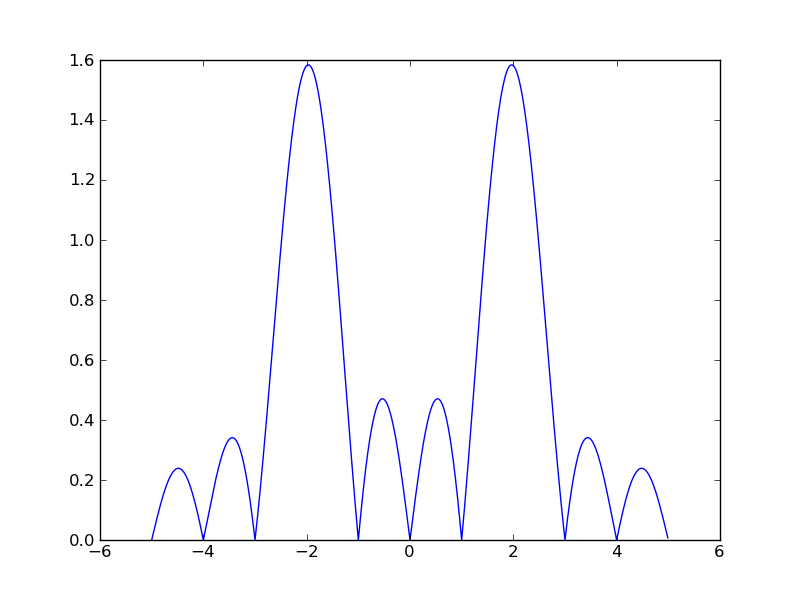
py.plot(f,np.abs(X))
py.show()
Powinno wytworzyć rysunek:
Zadanie 2: Związek autokorelacji z widmem sygnału
Oblicz gęstość widmową mocy sygnału zarejestrowanego w trakcie czuwania z zamkniętymi oczami, korzystając z twierdzenia Chinczyna oraz metodą Welcha. Znajdź częstość rytmu [math]\alpha[/math] dla osoby, która była badana.
Funkcja kowariancji i korelacji
Wstęp
W celu scharakteryzowania zależności wzajemnej dwóch sygnałów losowych, stosuje się funkcję kowariancji, zdefiniowaną w następujący sposób:
gdzie:
W przypadku sygnałów ciągłych estymację tę można zapisać w poniższy sposób:
natomiast dla sygnałów dyskretnych jako:
W odróżnieniu od funkcji autokowariancji, funkcja kowariancji nie musi mieć maksimum dla przesunięcia [math]\tau =0[/math]. Ponadto posiada ona następującą cechę:
Funkcję kowariancji można znormalizować:
Otrzymaną funkcję nazywamy funkcją korelacji. Jednym z zastosowań funkcji korelacji jest wyznaczanie czasu przejścia sygnału przez dany układ liniowy. Funkcja korelacji pomiędzy sygnałem na wejściu układu i sygnałem na jego wyjściu osiągnie wartość maksymalną dla przesunięcia [math]\tau [/math] równego czasowi, jaki potrzebował sygnał na pokonanie danego układu. Niestety, taka metoda wyznaczania opóźnienia obarczona jest pewną wadą — w przypadku gdy prędkość sygnału bądź jego droga zależą od częstości, wtedy na wykresie funkcji korelacji nie uzyskamy wyraźnego maksimum.
Zadanie 3: Funkcja kowariancji i korelacji
Zaimplementuj funkcję obliczającą funkcję kowariancji dla różnych sygnałów x i y (równanie 13) skorzystaj przy tym z własności opisanej równaniem (14). Przykładowe wywołanie:
a = np.array([1,2,3])
b = np.array([-1,-2,-3])
print koreluj(a,b,2)
powinno dać w wyniku:
[ 0.5 0. -1. 0. 0.5]
Z danych zarejestrowanych w trakcie czuwania z zamkniętymi oczami wybierz sygnały z następujących kanałów: Fp1, P3, Pz, P4, Fp2, O1, O2.
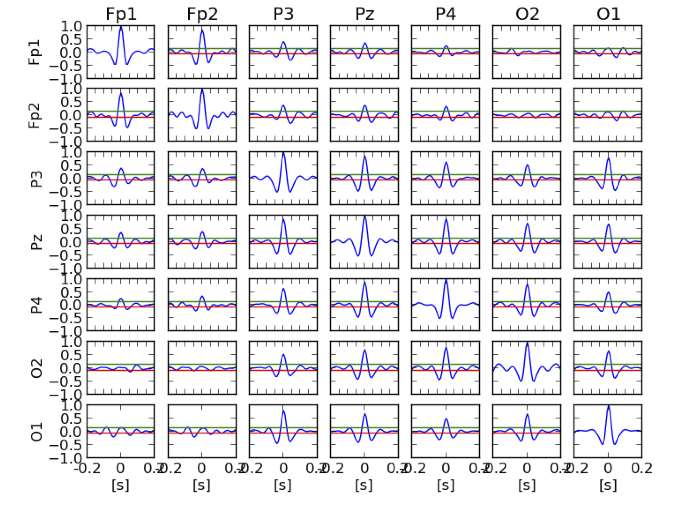
- Dla każdego kanału oblicz funkcję autokorelacji, zaś dla każdej pary kanałów oblicz funkcję korelacji wzajemnej. Wyniki zaprezentuj w formie kwadratowej macierzy wykresów (za pomocą funkcji subplot, tak jak na przykładowym rys. (rys. %i 1)). Na przekątnej macierzy narysuj funkcję autokorelacji odpowiednich kanałów, poza przekątną — funkcję korelacji wzajemnej. Wskaż kanały, które są najbardziej skorelowane ze sobą. Czy możliwe jest wyznaczenie opóźnienia sygnału pomiędzy tymi kanałami?
- Powtórz punkt 1, tym razem jednak funkcję autokorelacji i korelacji wzajemnej oblicz na sygnałach przefiltrowanych filtrem wąskopasmowym w paśmie alfa charakterystycznym dla badanej osoby. (przypomnienie konstrukcji filtrów)
-
Oszacuj istotność statystyczną zależności między parami kanałów. Twoją hipotezą zerową jest brak istotnej korelacji pomiędzy sygnałami zarejestrowanymi przez dwie różne elektrody EEG. Hipoteza alternatywna to występowanie zależności pomiędzy tymi sygnałami. Podanie estymatorów wariancji funkcji korelacji jest bardzo trudne, dlatego jednym ze sposobów oszacowania progu powyżej którego wartość funkcji korelacji można byłoby uznać za istotną statystycznie, jest zastosowanie metody bootstrap. Teoretycznie, funkcja korelacji policzona dla dwóch rzeczywistych, nieskorelowanych sygnałów, powinna wynosić 0 dla każdego przesunięcia [math]\tau[/math]. Tak jest jednak w przypadku sygnałów nieskończonych; w analizie sygnałów takowych nie spotkamy.
Dokonując losowej zamiany kolejności próbek, możemy doprowadzić do wytworzenia sygnałów zależnych losowo, które jednak ze względu na skończony czas trwania, dadzą niezerową funkcję korelacji. Poziom losowych fluktuacji tej funkcji oszacujemy wykonując następujące kroki:
- Losowa zamiana kolejności próbek w analizowanych sygnałach. Jeżeli pomiędzy dwoma sygnałami istnieją jakieś zależności, losowa zamiana próbek doprowadzi do zniszczenia tych związków. W ten sposób uzyskujemy sygnały, które teoretycznie są nieskorelowane.
- Obliczenie funkcji korelacji wzajemnej dla sygnałów policzonych w punkcie A.
- Powtórzenie kroków A i B wiele (np. 1000) razy.
- Oszacowanie 95 % przedziału ufności dla wartości średniej funkcji korelacji wzajemnej dla danego przesunięcia [math]\tau[/math] korzystając z otrzymanego w kroku C empirycznego rozkładu wartości tych funkcji dla sygnałów niezależnych.
- Powtórzenie kroków A-D dla kolejnych przesunięć [math]\tau[/math].
- Sprawdzenie, dla których przesunięć [math]\tau [/math] funkcje autokorelacji i korelacji obliczone dla oryginalnych sygnałów uzyskały wartości wyższe niż wartości progowe oszacowane dla sygnałów o losowych zależnościach.
Procedura opisana powyżej ma jednak pewną wadę. Staramy się w niej oszacować poziom przypadkowych korelacji pomiędzy dwoma sygnałami dla kolejnych przesunięć [math]\tau [/math], co jest niczym innym jak wielokrotnym powtórzeniem pewnego testu. Obserwowanie korelacji dla wielu par kanałów równocześnie również prowadzi do zwiększenia szansy na zaobserwowanie ekstremalnie dużych fluktuacji. Występuje tu zatem problem wielokrotnych porównań. Przypominamy, iż może to doprowadzić do przypadkowego uznania wyników jako „istotnych” statystycznie. Np. jeśli pojedynczy test wykonujemy na poziomie istotności 5% to dopuszczamy odrzucenie w 1 przypadku na 20 hipotezy zerowej pomimo, iż jest ona prawdziwa. Z drugiej jednak strony, jeśli powtórzymy wykonywany test 20 razy, to oczekujemy uzyskania 1 przypadku, w którym poziom [math]p[/math] będzie mniejszy od 5% co jest przesłanką za odrzuceniem hipotezy zerowej.
W przypadku wykonywania serii testów należałoby więc zastosować odpowiednie poprawki, np. korektę Bonferroniego czy false discovery rate (FDR). Innym rozwiązaniem w analizowanym przez nas problemie jest zastosowanie tzw. statystyk wartości ekstremalnych, które prowadzą do następujących zmian w procedurze (nie działa dla funkcji autokorelacji ze względu na jej normalizację do 1 dla zerowego przesunięcia):
- Losowa zmiana kolejności próbek w analizowanych sygnałach (we wszystkich analizowanych kanałach). Jeżeli pomiędzy dwoma sygnałami istnieją jakieś zależności, losowa zamiana próbek doprowadzi do zniszczenia tych związków. W ten sposób uzyskujemy sygnały, które teoretycznie są nieskorelowane.
- Obliczenie funkcji korelacji dla sygnałów otrzymanych w punkcie A.
- Zapamiętanie maksymalnej wartości bezwzględnej funkcji korelacji z punktu B (maksimum bierzemy po wszystkich przesunięciach i po wszystkich parach kanałów).
- Powtórzenie kroków A-C 1000 razy. Uzyskamy w ten sposób rozkład maksymalnych wartości funkcji korelacji możliwych do zaobserwowania dla sygnałów niezależnych.
- Wyznaczenie 95 centyla rozkładu wartości maksymalnych.
- Nałożenie na rysunki funkcji korelacji uzyskane w Zadaniu 2 poziomych linii symbolizujących poziom zależności dwóch sygnałów o losowych zależnościach i sprawdzenie, dla których przesunięć [math]\tau [/math] wartości funkcji korelacji przekraczają estymowane progi istotności statystycznej.
Wzajemna gęstość widmowa sygnałów i koherencja
--> to chyba przeniesiemy do Labu
Zadanie 4: Wzajemna gęstość widmowa sygnałów i koherencja
Wstęp
Podobnie jak w przypadku twierdzenia Chinczyna dla pojedynczego sygnału, możliwe jest policzenie transformaty Fouriera funkcji kowariancji. Uzyskana w ten sposób wielkość nazywa się funkcją wzajemnej gęstości mocy widmowej sygnału:
W celu dalszego omówienia własności funkcji wzajemnej mocy widmowej sygnałów funkcję tę zapiszemy w postaci:
Wartość bezwzględna funkcji wzajemnej gęstości mocy widmowej osiąga największą wartość dla częstości, w których sygnały [math]x(t)[/math] i [math]y(t)[/math] są ze sobą skorelowane. Funkcja wzajemnej mocy widmowej sygnałów pozbawiona jest zatem wady, która charakteryzowała funkcję korelacji, to jest problemu z wyznaczeniem czasu transmisji sygnału, w przypadku gdy czas ten zależał od częstości. Przy pomocy funkcji wzajemnej mocy widmowej, czas ten można oszacować przy pomocy fazy tej funkcji — [math]\phi _{xy}(f)[/math]. Jeśli funkcja wzajemnej mocy widmowej została wyznaczona pomiędzy sygnałami na wejściu i wyjściu układu liniowego, to faza ta reprezentuje przesunięcie fazowe sygnału przy przejściu przez układ. Czas tego przejścia można oszacować za pomocą następującej wyrażenia:
Podobnie jak w przypadku funkcji autokorelacji i korelacji wzajemnej, funkcję wzajemnej gęstości mocy widmowej można znormalizować:
Znormalizowaną postać funkcji wzajemnej gęstości mocy widmowej nazywamy funkcją koherencji. Koherencja jest wielkością zespoloną. Faza koherencji odzwierciedla różnicę faz pomiędzy dwoma sygnałami. Moduł koherencji reprezentuje stopień synchronizacji sygnałów i zawiera się w przedziale od 0.0 do 1.0. Moduł tej funkcji zawiera się w przedziale od 0 do 1. Wartości 0 odpowiada brak synchronizacji pomiędzy sygnałami, zaś wartości 1 pełna synchronizacja dwóch przebiegów czasowych. Należy również zwrócić uwagę na nazewnictwo - często sam moduł koherencji określany jest jako koherencja, w literaturze anglojęzycznej moduł koherencji posiada jednak odrębną nazwę: Magnitude Square Coherence (MSC). Istotny jest również sposób estymacji modułu koherencji, który wyprowadzono w następnym rozdziale, zaś sam estymator reprezentuje wzór (36).
Kilka słów o koherencji
Wzór (Equation 19), definiujący ilościową miarę koherencji, nie uwzględnia stochastycznego charakteru sygnałów. Łatwo zauważyć, że bezpośrednie zastosowanie tego wzoru do obliczenia koherencji dwóch sygnałów o tej samej częstości i różniących się jedynie amplitudą oraz fazą, zawsze da wynik równy 1. Prześledźmy to na następującym przykładzie.
Dane są dwa sygnały harmoniczne [math]x(t) = A\cos(\Omega t + \phi_x)[/math] oraz [math]y(t) = B\cos(\Omega t + \phi_y)[/math].
Widmo tych sygnałów, wyrażone za pomocą transformaty Fouriera, będzie miało następującą postać:
[math]X(f)=Ae^{-j\phi_x}[/math]
[math]Y(f)=Be^{-j\phi_y}[/math],
zaś ich widmo wzajemne:
[math]X(f)\cdot Y^*(f) = A\cdot Be^{-j(\phi_x - \phi_y)}[/math],
gdzie: [math]j=\sqrt{-1}[/math], a * oznacza sprzężenie liczby zespolonej.
Podstawienie wyrażeń na widmo sygnałów [math]x(t)[/math], [math]y(t)[/math] oraz ich widmo wzajemne do wzoru ??? da koherencję [math]K_{xy}(f) = 1[/math] niezależnie od amplitudy sygnałów [math]A[/math] i [math]B[/math] oraz ich faz [math]\phi_x[/math] i [math]\phi_y[/math].
W praktyce rzadko jednak mamy do czynienia z sygnałami harmonicznymi. Zwykle mierzone przez nas wielkości mają stochastyczny charakter bądź też ich pomiar jest zaburzany przez różne czynniki.
Rozważmy teraz najprostszy model pomiaru sygnału, w którym uwzględniono wpływ zakłóceń w postaci białego szumu. Na wejście układu LTI o funkcji impulsowej opisanej wyrażeniem [math]h(t)[/math] podamy sygnał [math]x(t)[/math] i widmie danym funkcją [math]X(f)[/math]. Układ LTI przetworzy sygnał wejściowy na przebieg [math]y(t)[/math] o widmie [math]Y(f)[/math]. Z uwagi na zaburzenia [math]n(t)[/math] o widmie [math]N(f)[/math] towarzyszące pomiarowi aparatura nie zarejestruje sygnał [math]y(t)[/math] lecz [math]z(t) = y(t) + n(t)[/math]. Opisane zależności możemy opisać za pomocą poniższych wzorów:
[math]y(t) = h(t)*x(t)[/math]
[math]z(t) = y(t) + n(t)[/math]
gdzie: [math]*[/math] - operacja splotu.
Dokonując transformacji powyższych wzorów do dziedziny częstości dostajemy:
[math]Y(f) = H(f)X(f)[/math]
[math]Z(f) = Y(f) + N(f)[/math]
gdzie: [math]H(f) = \textrm{FFT}\left\{h(t)\right\}[/math].
Wzory te można zapisać w postaci jednej zależności:
Załóżmy teraz, że w celu redukcji składowej losowej [math]n(t)[/math] wielokrotnie powtarzamy w tych samych warunkach pomiar sygnału [math]z(t)[/math]. Za każdym razem na wejściu układu LTI występuje ten sam sygnał [math]x(t)[/math]. Układ LTI również przetwarza sygnał wejściowy w ten sam sposób, jednak z uwagi na stochastyczny charakter zakłóceń, otrzymujemy kolejne różniące się do siebie przebiegi [math]z_i(t)[/math]. Niech liczbę powtórzeń pomiaru wynosi [math]K[/math]. Możemy napisać [math]K[/math] równań opisujących relację pomiędzy sygnałem wejściowym, wyjściowym i mierzonym:
Przemnóżmy teraz równania (Equation 21) obustronnie przez sprzężone widmo sygnału rejestrowanego [math]Z(f)[/math]. Dla uproszczenia zapisu operacji dokonamy na jednym, dowolnie wybranym [math]i[/math]-tym równaniu:
Na równaniu (Equation 22) dokonamy kolejno następujących przekształceń:
Dokonajmy teraz uśredniania (Equation 24) po kolejnych powtórzeniach pomiaru.
Zakładamy, że szum [math]N(f)[/math] jest nieskorelowany z sygnałem wejściowym, w związku z czym w wyniku uśredniania dwa ostatnie składniki równania (Equation 25) zostaną zredukowane: [math]\left\langle H(f)X(f)N_i^*(f)\right\rangle \approx 0 [/math], [math]\left\langle N_i(f)H^*(f)X^*(f)\right\rangle \approx 0 [/math]. Założyliśmy również za każdym razem na wejściu układu liniowego pojawia się ten sam sygnał [math]x(t)[/math], sam układ zaś nie zmienia swoich właściwości, w zwiazku z czym: [math]\left\langle|H(f)|^2|X(f)|^2\right\rangle = |H(f)|^2|X(f)|^2 [/math]. Ostatecznie uzyskaliśmy następującą zależność:
Dokonajmy kolejnego przekształcenia równania (Equation 21). tym razem przemnożymy obustronnie każde równanie przez sprzężone widmo sygnału wejściowego. W celu uproszczenia zapisu, operację tę wykonamy tylko na jednym dowolnie wybranym [math]i[/math]-tym równaniu:
,
gdzie: [math]Z_i(f)X^*(f)[/math] - to widmo wzajemne sygnałów [math]x(t)[/math] i [math]y(t)[/math]. Proste przekształcenie równania (Equation 27) prowadzi do następującego wyrażenia:
Uśrednimy teraz równanie (Equation 28) po kolejnych realizacjach pomiaru oraz obliczmy moduł uzyskanego wyniku:
Brak korelacji pomiędzy szumem [math]n(t)[/math] a sygnałem wejściowym [math]x(t)[/math] powoduje, że w wyniku uśredniania zostaje zredukowany drugi składnik równania (Equation 29): [math]\left\langle N_i(f)X^*(f)\right\rangle \approx 0[/math]. Ostatecznie uzyskujemy następującą zależność:
która wraz z równaniem (Equation 26) tworzy układ równań opisujących relacje pomiędzy widmami i widmami mocy sygnałów występujących w naszym modelu:
- [math] \left\langle|Z_i(f)|^2\right\rangle= |H(f)|^2 |X(f)|^2 + \left\langle|N_i(f)|^2\right\rangle [/math]
Z pierwszej zależności równania (Equation 31) wyznaczmy funkcję przejścia [math]|H(f)|[/math]:
[math]|H(f)| = \frac{|\left\langle Z_i(f)X^*(f)\right\rangle|}{|X(f)|^2}[/math]
i podstawy do drugiego równania układu (Equation 31). Otrzymujemy:
Równanie (Equation 32) możemy przekształcić do postaci:
a następnie do zależności:
Wyrażenie:
nazywana jest Magnitude Square Coherence pomiędzy sygnałami [math]x(t)[/math] i [math]z(t)[/math]. W przypadku, gdy wielkość ta jest równa 1 sygnały [math]x(t)[/math] i [math]z(t)[/math] są w pełni zsynchronizowane. Wielkość tę uzyskaliśmy dla sygnału na wejściu układu LTI oraz sygnału mierzonego na wyjściu. Funkcję MSC można jednak stosować do dowolnych dwóch sygnałów stochastycznych [math]x(t)[/math] i [math]y(t)[/math] przy założeniu, że istnieją pomiędzy nimi liniowe zależności:
gdzie: [math]\lt \gt [/math] - oznacza wartość średnia, [math]X_i(f), Y_i(f) [/math] to zespolone widma (policzone np. za pomocą Transformaty Fouriera), wyznaczone odpowiednio dla sygnałów X oraz Y w "i-tej" realizacji eksperymentu lub w "i-tym" oknie czasowym, na który te sygnały zostały podzielone. Wzór (36) reprezentuje estymator wartości bezwzględnej koherencji. Opierając się na podobnym co wyżej rozumowaniu, można wyprowadzić estymator funkcji koherencji, o następującej postaci:
Faza koherencji umożliwia nam estymację przesunięcia fazowego pomiędzy sygnałami X i Y, zaś moduł podniesiony do kwadratu funkcji C to MSC.
Polecenie 2
Zaimplementuj funkcję obliczającą koherencję dla pary kanałów. Oblicz i narysuj funkcję koherencji dla kolejnych par kanałów (tych samych co w zadaniu 3). Wyniki zaprezentuj w postaci kwadratowej macierzy rysunków. Ponieważ koherencja jest funkcją zespoloną, dobrze jest zaprezentować osobno jej wartość i fazę. Uzyskane wartości bezwzględne koherencje narysuj nad przekątną tej macierzy, a fazę pod przekątną. W celu obliczenia modułu koherencji i jej fazy wykorzystaj wzór 36 (wygenerowane sygnały należy podzielić na pewną liczbę odcinków)