PPy3/Matplotlib
Spis treści
Matplotlib - wizualizacja danych
Wprowadzenie do pakietu Matplotlib na przykładach
Pakiet Matplotlib bazuje na pakiecie numerycznym Numpy i korzysta z obiektów w nim zawartych. Pokażemy, jak z jego pomocą rysować różnorodne wykresy prezentujące graficznie przetwarzane dane i wyniki obliczeń. Zamiast wyliczać zawartość pakietu pokażemy ich użyteczność na przykładach. Zaczniemy od prostych i będziemy po drodze omawiać zastosowane w nich konstrukcje.
Wykresy funkcji
y = f(x)
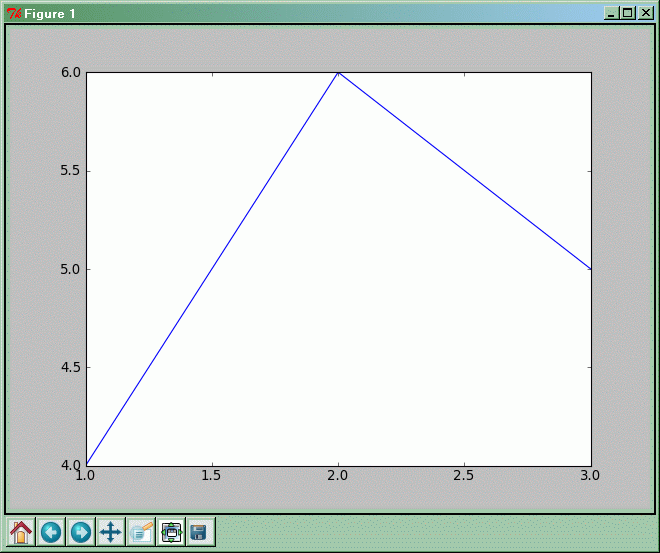
Prześledźmy działanie poniższego programu:
import matplotlib.pyplot as plt
x = [1,2,3]
y = [4,6,5]
plt.plot(x,y)
plt.show()
- Rezultat
- Jak to działa?
Aby skorzystać z pakietu graficznego Matplotlib importujemy go do naszego programu poleceniem import.
Pod-pakiet pyplot jest jednym z paru nieco różnych interfejsów do Matplotlib - tj. sposobów wykorzystania jego funkcjonalności. Inny, też często wykorzystywany, nazywa się pylab i można go importować wprost (import pylab). Pyplot zapewnie nieco większą elastyczność, chociaż dla najprostszych przykładów - takich, jakie tu omówimy - nie ma istotnej różnicy.
Wytwarzamy dwie listy x i y zawierające ciągi liczb 1, 2, 3 oraz 4, 6, 5.
Funkcja plot rysuje wykres i umieszcza na nim punkty o współrzędnych zawartych w listach przekazanych jej jako argumenty. Pierwszy argument zawiera współrzędne x-owe kolejnych punktów, a drugi argument współrzędne y-owe kolejnych punktów wykresu. Ponieważ listy mają po trzy elementy, tak więc wykres zawierać będzie trzy punkty o współrzędnych (1, 4), (2, 6) oraz (3, 5). Domyślnie punkty na wykresie łączone są ze sobą niebieską linią ciągłą. To oczywiście można zmienić - dodając opcjonalne parametry do wywołania plot można uzyskać linię o innym kolorze, linię przerywaną, z kropek, albo w ogóle brak linii - a za to np. duże kropki (trójkąty, gwiazdki, ...) w miejscach odpowiadających punktom danych.
Po wywołaniu funkcji plot wykres nie pokazuje się jeszcze na ekranie. Aby go pokazać, używamy funkcji show. Wykres pojawia się na ekranie w osobnym oknie, a Python czeka z wykonywaniem kolejnych instrukcji do momentu zamknięcia okna z wykresem.
W okienku wykresu mamy kilka guzików (po lewej stronie na dole). Służą one do manipulowania wyglądem rysunku. Guzikiem z krzyżykiem możemy zmniejszać/zwiększać skalę na osiach (wciskając prawy guzik myszy i przesuwając kursor po obrazku) oraz przesuwać cały wykres (wciskając lewy guzik myszy i przesuwając kursor po obrazku). Guzik z okienkiem i strzałkami pozwala także zmieniać rozmiar i położenie osi wykresu wewnątrz okna wybierając właściwe wartości. Guzik z domkiem przywraca wyjściowe ustawienia rysunku. Guzik z obrazkiem dyskietki (czy ktoś jeszcze wie, co to takiego?) pozwala zachować wykres (jego aktualny stan, czyli z uwzględnieniem dokonanych interaktywnie modyfikacji) jako plik graficzny jednego z kilku formatów.
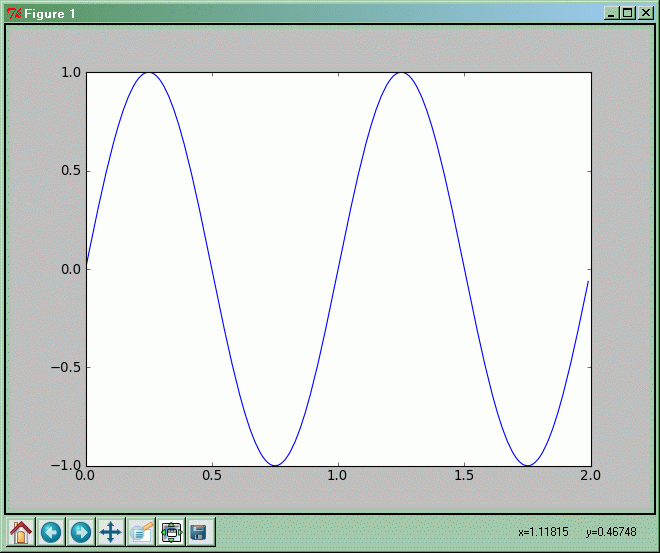
Rysujemy wykres funkcji sinus
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(0.0, 2.0, 0.01)
y = np.sin(2.0*np.pi*x)
plt.plot(x,y)
plt.show()
- Rezultat
- Jak to działa?
Oprócz funkcji z Matplotlib będziemu tu odwoływać się również wprost do elementów z pakietu NumPy.
Funkcja arange jest podobna do standardowej funkcji range wytwarzającej określone sekwencje liczb w postaci listy. Funkcja arange zamiast listy wytwarza tablicę zawierającą ciąg liczb zmiennoprzecinkowych zaczynający się od pierwszego podanego argumentu funkcji arange (u nas 0.0), a kończący się przed drugim argumentem (tradycyjnie, ciąg wynikowy nie zawiera wartości podanej jako drugi argument, u nas 2.0). Różnica między elementami wytworzonego ciągu domyślnie wynosi 1, ale jeśli podamy funkcji arange trzeci argument, to definiuje on nową różnicę ciągu, u nas wynosi on 0.01.
Tak więc zmienna x jest tablicą-wektorem zawierającą ciąg liczb od 0 do 1,99 co 0,01 (czyli 0, 0,01, 0,02, ..., 1,98, 1,99).
Funkcja sin służy do obliczania wartości funkcji sinus dla argumentu podanego w radianach. A co u nas jest argumentem tej funkcji? Wyrażenie będące argumentem zawiera mnożenie liczby 2.0 przez pi (pochodzące z pakietu NumPy), a następnie mnożenie wyniku przez tablicę x. Zmienna pi zawiera przybliżoną wartość matematycznej stałej π ≈ 3,1415926... Mnożenie liczby i tablicy, jak wiemy z poprzedniego punktu, daje w wyniku tablicę. Oznacza to, że argumentem funkcji sin jest nie liczba, ale tablica! Taka możliwość jest przewidziana przez twórców pakietu Numpy; wynikiem wywołania funkcji jest wtedy również tablica. Jest ona tej samej długości co tablica będąca argumentem wywołania funkcji.
Tak więc zmienna y zawiera ciąg wartości funkcji sinus policzonych dla wartości zawartych w zmiennej x pomnożonych każda przez 2π (czyli sin(2π·0), sin(2π·0,01), sin(2π·0,02), ..., sin(2π·1,98), sin(2π·1,99)).
Funkcja plot(x,y) narysuje zestaw punktów o współrzędnych (0, sin(2π·0)), (0,01, sin(2π·0,01)), (0,02, sin(2π·0,02)), ..., (1,98, sin(2π·1,98)), (1,99, sin(2π·1,99)) połączonych niebieską linią.
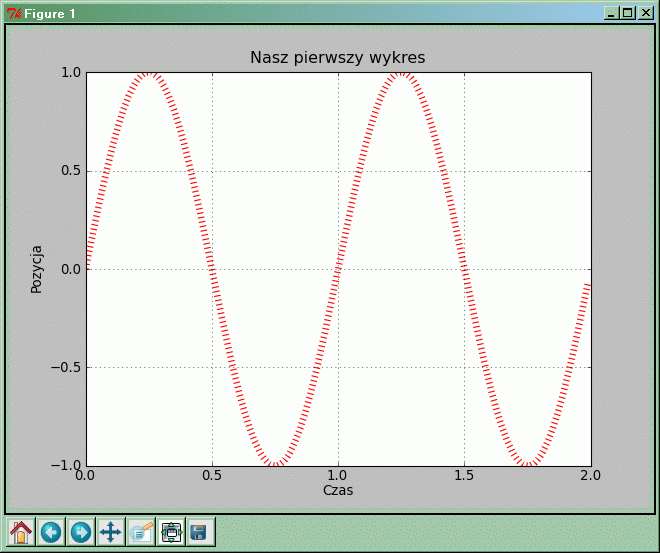
Ulepszamy wykres
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(0.0, 2.0, 0.01)
y = np.sin(2.0*p.pi*x)
plt.plot(x,y,'r:',linewidth=6)
plt.xlabel('Czas')
plt.ylabel('Pozycja')
plt.title('Nasz pierwszy wykres')
plt.grid(True)
plt.show()
- Rezultat
- Jak to działa?
W porównaniu z poprzednim przykładem pojawiło się na wykresie kilka drobnych zmian i „ozdobników”.
W funkcji plot pojawiły się dwa nowe parametry:
- 'r:' — ten parametr steruje wyglądem rysowanej linii wykresu. Pierwsza litera tego napisu określa kolor linii (na przykład r: czerwony, b: niebieski, g: zielony, y: żółty, k: czarny). Drugi znak napisu określa wygląd samej linii (np. -: ciągła, :: kropkowana, o: okrągłe punkty bez linii, +: krzyżyki bez linii, itd.).
- linewidth=6 — ten parametr zmienia grubość rysowanej linii.
Dodaliśmy też wywołania funkcji xlabel i ylabel. Ich argumentami są napisy, które pojawią się jako opisy osi, odpowiednio poziomej i pionowej. Wywołanie funkcji title wypisuje przekazany jej napis jako tytuł całego wykresu.
Funkcja grid dorysowuje siatkę prostokątną na wykresie w wybranych punktach opisujących wartości na osiach wykresu. Punkty, w których wybierane są wartości opisane na osiach (ang. tick) są wybierane automatycznie (oczywiście jeśli chcemy, możemy zmieniać ich położenie i opisy odpowiednią funkcją, powiemy o tym później).