WnioskowanieStatystyczne/CLT

Wnioskowanie_Statystyczne_-_wykład

Rozkład Gaussa

Rozkład Gaussa (zwany też rozkładem normalnym lub krzywą dzwonową) zależy od parametrów [math]\mu[/math] i [math]\sigma[/math]. Jego gęstość prawdopodobieństwa określona jest wzorem:

[math] p(x)=N(\mu, \sigma)= \frac{1}{\sqrt{2\pi }\sigma }e^{\frac{-(x-\mu )^{2}}{2\sigma ^{2}}}. [/math]

Parametry te są tak dobrane, że wartość oczekiwana wynosi [math]\mu[/math], a wariancja [math]\sigma^2[/math].

[math]N(0,1)[/math], czyli standardowy rozkład Gaussa o zerowej średniej ([math]\mu=0[/math]) i jednostkowej wariancji ([math]\sigma=1[/math]).

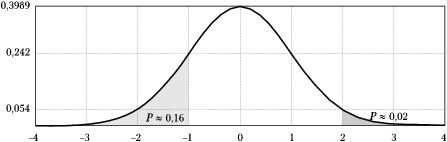
Rozkład Gaussa dla zerowej wartości oczekiwanej i jednostkowej wariancji ([math]\mu=0, \sigma^2=1[/math]) zwiemy standardowym rozkładem Gaussa i oznaczamy zwykle [math]N(0,1)[/math]. Na wykresie zaznaczono na nim m. in. wartość całki od [math]-\infty[/math] do [math]-1[/math], czyli prawdopodobieństwo, że wylosowana z tego rozkładu liczba będzie mniejsza niż [math]-1[/math]. Jak widać, wynosi ono ok. 16%, a jeśli weźmiemy pod uwagę również wartości większe od 1, będzie to aż 32%! Oznacza to, że przy losowaniu wielu liczb z tego rozkładu niemal 1/3 wyników może znaleźć się w odległości większej niż [math]\sigma[/math] od wartości oczekiwanej.

[math] x\in N(\mu,\sigma)\quad \Rightarrow \quad \begin{cases} P(\left| x-\mu \right| \geq \sigma )\approx 0,\!317,\\ P(\left| x-\mu \right| \geq 2\sigma )\ \approx 0,\!046,\\ \ P(\left| x-\mu \right| \geq 3\sigma )\approx 0,\!003. \end{cases} [/math]

Rozkład Gaussa pełni w statystyce bardzo znaczącą rolę ze względu na Centralne Twierdzenie Graniczne, mówiące o asysmptotycznym rozkładzie sumy dużej liczby niezależnych zmiennych losowych, których rozkłady spełniają pewne warunki. Udowodnimy je w najprostszym przypadku, kiedy wszystkie te zmienne pochodzą z tego samego rozkładu gęstości prawdopodobieństwa. Na potrzeby tego dowodu musimy najpierw wprowadzić pojęcie funkcji charakterystycznej.

Funkcja charakterystyczna rozkładu prawdopodobieństwa

Dla zmiennej losowej [math]x[/math] jest to wartość oczekiwana wyrażenia [math]e^{itx}[/math], gdzie [math]i=\sqrt{-1}[/math]. Dla rozkładów ciągłych jest to transformata Fouriera funkcji gęstości prawdopodobieństwa [math]f(x)[/math]:

[math] \phi_x (t)=E(e^{itx})=\underset{-\infty }{\overset{\infty }{\int }} e^{itx}f\left( x\right) dx [/math]

Użyteczne będą poniższe związki, które wyprowadzić można bezpośrednio z definicji:

Funkcja charakterystyczna rozkładu sumy zmiennych niezależnych

Dla niezależnych zmiennych [math]x[/math] i [math]y[/math]:

[math] w=x+y\Rightarrow \phi _{w}(t) =\phi _{x}\left( t\right) \cdot \phi_{y}(t). [/math]

Dowód:

[math] \phi _{w}(t) = E(e^{it(x+y)})=E(e^{itx}\cdot e^{ity}) = E(e^{itx})\cdot E(e^{ity})=\phi _{x}\left( t\right) \cdot \phi_{y}(t). [/math]

Pochodna funkcji charakterystycznej

Bezpośrednio z definicji (różniczkujemy po [math]dt[/math], więc przy każdym różniczkowaniu spada nam z wykładnika [math]i x[/math], [math]x[/math] zostaje pod całką a [math]i[/math] jako stała wychodzi przed całkę) widać, że:

[math] \frac{d^{n}\phi (t)}{dt^{n}}=i^{n}\underset{}{\underset{-\infty }{\overset{ \infty }{\int }}x^{n}}\ e^{itx}f(x) dx [/math]

Związek pochodnej funkcji charakterystycznej z momentami zmiennej losowej

[math]n[/math]-ta pochodna funkcji charakterystycznej w zerze (czyli dla [math]t=0[/math]) wynosi

[math] \phi^{(n)}(0)= i^{n}\underset{}{\underset{-\infty }{\overset{\infty }{\int }}x^{n}}\ e^{i 0 x} f(x) dx = i^{n}\underset{}{\underset{-\infty }{\overset{\infty }{\int }}x^{n}} f(x) dx = i^{n}E(x^{n}) [/math]

Twierdzenie Lindeberga–Lévy'ego

Zakładamy, że [math]x_{i}[/math] są niezależnymi zmiennymi podlegającymi (dowolnemu) rozkładowi o skończonej wartości oczekiwanej [math]\mu[/math] i wariancji [math]\sigma^{2}[/math] — czyli wszystkie sumowanie zmienne [math]x_i[/math] pochodzą z tego samego rozkładu prawdopodobieństwa, o którym nie zakładamy nic ponad to, że ma skończone [math]\mu[/math] i [math]\sigma[/math]. Dla [math]n\rightarrow \infty[/math], wielkość

[math] S=\dfrac{ \sum\limits_{i=1}^{n}x_{i}\; -\; n\mu}{\sigma \sqrt{n}} [/math]

podlega rozkładowi normalnemu o wartości średniej 0 i wariancji 1.

Dowód twierdzenia Lindeberga–Lévy'ego

Rozważmy zmienną [math]y_i[/math] o zerowej wartości oczekiwanej i jednostkowej wariancji

[math] y_{i} = \dfrac{x_{i}-\mu}{\sigma} . [/math]

Funkcję charakterystyczną rozkładu zmiennej [math]y_i[/math]

[math]\phi_{y_i}(z) = E(e^{i z y_i}) [/math]

możemy rozwinąć w szereg Taylora wokół [math]z=0[/math]

[math] \phi_{y_i}(z)=\underset{n=0}{\overset{\infty }{\sum }}\frac{\phi^{(n)}(0)}{n!}z^n [/math]

Z wyprowadzonej wcześniej własności funkcji charakterystycznej (4) [math] \phi^{(n)}(0)= i^{n}E(x^{n}) [/math] wynika, że

[math]\phi_{y_i}^{(0)}(0)=1[/math],

[math]\phi_{y_i}^{(1)}(0)=0[/math] (wartość oczekiwana),

[math]\phi_{y_i}^{(2)}(0)=-1[/math] ([math]i^2[/math] * wariancja),

czyli funkcja charakterystyczna zmiennej [math]y_i[/math] rozwinięta w szereg Taylora (6) do wyrazów drugiego rzędu będzie miała postać

[math] \phi_{y_i}(z)=1-\frac{z^{2}}{2}+\cdots . [/math]

Wrócmy do występującej w twierdzeniu sumy [math]S[/math]

[math] S=\dfrac{ \sum\limits_{i=1}^{n}x_{i}\; -\; n\mu}{\sigma \sqrt{n}} = \dfrac{1}{\sigma \sqrt{n}} \sum\limits_{i=1}^{n}(x_{i} -\mu) = \dfrac{1}{\sqrt{n}} \sum\limits_{i=1}^{n}\dfrac{x_{i} -\mu}{\sigma} = \dfrac{1}{\sqrt{n}} \sum\limits_{i=1}^{n} y_i [/math]

Jej funkcja charakterystyczna

[math]\phi_S(z) = E(e^{izS}) = E\left(e^{iz \frac{1}{\sqrt{n}} \sum\limits_{i=1}^{n} y_i} \right) [/math] [math] = E\left(\prod_{i=1}^{n} e^{iz \frac{1}{\sqrt{n}} y_i} \right) [/math]

ponieważ zmienne [math]y_i[/math] są wzajemnie niezależne,

[math]\phi_S(z)= \prod_{i=1}^{n} E\left( e^{i\frac{z}{\sqrt{n}} y_i } \right) = \prod_{i=1}^{n} \phi_{y_i}\left(\frac{z}{\sqrt{n}}\right) [/math]

ponieważ zmienne [math]y_i[/math] pochodzą z tego samego rozkładu prawdopodobieństwa,

[math]\phi_S(z)= \prod_{i=1}^{n} \phi_{y_i}\left(\frac{z}{\sqrt{n}}\right) = \left( \phi_{y_i}\left(\frac{z}{\sqrt{n}}\right) \right)^n = \left( 1-\frac{(z/\sqrt{n})^{2}}{2}+\cdots \right)^n = \left( 1-\frac{z^2}{2n}+\cdots \right)^n [/math]

Przy przejściu z [math]n[/math] do nieskończoności (i pomijaniu wyrazów rzędu wyższego niż drugi) dostajemy

[math] \phi_y(z)\rightarrow \underset{n\rightarrow \infty }{\lim }\left(1-\frac{z^2}{2n}\right)^n= e^{\frac{-z^{2}}{2}} [/math]

bo [math]e^x=\lim_{n\rightarrow\infty} (1+x/n)^n[/math]

Pozostaje pokazać, że jest to postać funkcji charakterystycznej rozkładu Gaussa.

Transformata Fouriera funkcji Gaussa

Funkcja charakterystyczna rozkładu normalnego o wartości oczekiwanej 0 i jednostkowej wariancji będzie miała postać

[math] \phi _{x}(t)= \int\limits_{-\infty}^\infty e^{itx}\frac{1}{\sqrt{2\pi }} e^{\frac{-x^{2}}{2}} dx = [/math]

[math] \dfrac{1}{\sqrt{2\pi}} \int\limits_{-\infty}^\infty \left( \cos(tx) + i \sin(tx) \right) e^{\frac{-x^2}{2}} dx = [/math]

[math] \dfrac{1}{\sqrt{2\pi}} \int\limits_{-\infty}^\infty \cos(tx) e^{\frac{-x^2}{2}} dx + \dfrac{1}{\sqrt{2\pi}} \int\limits_{-\infty}^\infty i \sin(tx) e^{\frac{-x^2}{2}} dx [/math]

ponieważ funkcja [math]\sin(x)[/math] jest antysymetryczna, druga całka znika. Dostajemy

[math] \int\limits_{-\infty}^\infty e^{itx}\frac{1}{\sqrt{2\pi }} e^{\frac{-x^2}{2}} dx = \dfrac{1}{\sqrt{2\pi}} \int\limits_{-\infty}^\infty \cos(tx) e^{\frac{-x^2}{2}} dx [/math]

Dla części symetrycznej znajdujemy w tablicach całkę oznaczoną

[math] \int\limits_{0}^{\infty} e^{-a^2 x^2} \cos(b x) dx = \frac{ \sqrt{\pi} e^{-\tfrac{b^2}{4a^2}} } {2 a} [/math]

po wymnożeniu przez 2 i podstawieniu [math] b=t[/math] i [math]a^2=\frac{1}{2}[/math] dostajemy

[math] \int\limits_{-\infty}^{\infty} e^{-\frac{1}{2} x^2} \cos(t x) dx = \frac{ \sqrt{\pi} e^{ -\frac{t^2} { 4 \frac{1}{2} } } } {\frac{1}{\sqrt{2}}} = \sqrt{2\pi} e^{-\frac{t^2}{2}} [/math] , czyli

[math] \phi _{x}(t) = \int\limits_{-\infty}^\infty e^{itx}\frac{1}{\sqrt{2\pi }} e^{\frac{-x^{2}}{2}} dx = e^{-t^2 / 2} [/math]

W analizie sygnałów wynik ten będzie oznaczał, że transformacja Fouriera funkcji Gaussa jest funkcją Gaussa. W tym konkretnym przypadku otrzymaliśmy funkcję tożsamą z funkcją charakterystyczną rozkładu rozważanej sumy zmiennych, czyli rozkład ten będzie (w przypadku granicznym) miał postać funkcji Gaussa.

Ilustracja działania Centralnego Twierdzenia Granicznego. Zmienną [math]x_i[/math] bierzemy z rozkładu równomiernego, kolejne histogramy przedstawiają sumę 2, 3 i 4 zmiennych [math]x_i[/math] dla 10 000 losowań. Widać dużą zgodność z dopasowanym rozkładem normalnym (ciągła linia) już dla niewielu sumowanych zmiennych.

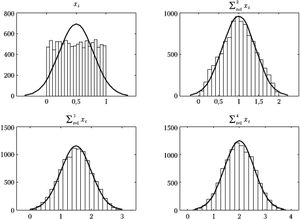
Rysunek 1 ilustruje powyższe twierdzenie dla przypadku sumy zmiennych pochodzących z rozkładu równomiernego. Jak widać, już dla sumy 3 zmiennych rozkład wydaje się bardzo podobny do normalnego. Niestety, często istotne bywają różnice dla wartości bardzo dużych lub bardzo małych. Otóż według wzoru wartości gęstości prawdopodobieństwa rozkładu normalnego dążą do zera dla dużych wartości bezwzględnych zmiennej asymptotycznie, lecz zera faktycznie nie osiągają. Inaczej mówiąc, prawdopodobieństwo wylosowania dowolnie dużej wartości z rozkładu Gaussa będzie małe, ale nie zerowe. Za to suma np. czterech zmiennych z rozkładu równomiernego od zera do jedynki (prawy dolny wykres rys. 1) nie przekroczy nigdy wartości 4, czyli prawdopodobieństwo dla [math]x\gt 4[/math] będzie dokładnie zerem. I choć w skali rysunku 1 efekt ten jest prawie niewidoczny, warto pamiętać, że testy oparte na założeniu normalności rozkładów często operują właśnie w okolicach tych "ogonów", gdzie przybliżenie rozkładu normalnego, uzyskane za pomocą tej prostej procedury, zawodzi.

---