Elektrodynamika/Seria 2: Różnice pomiędzy wersjami
SuperAdmin (dyskusja | edycje) (Utworzono nową stronę "<div align="center"> <b>Elektrodynamika dla Neuroinformatyki</b> <b>Seria 2</b> </div> ==Zadanie 1== Dwa ładunki punktowe <math> 3q </math> oraz <math> -q </math>...") |
SuperAdmin (dyskusja | edycje) |
||
| Linia 18: | Linia 18: | ||
! | ! | ||
|- | |- | ||
| − | | | + | | [[File:seria2_3.png|150px|left]] |
| <figure id="uid2">[[File:seria2_4.png|150px|left]]</figure> | | <figure id="uid2">[[File:seria2_4.png|150px|left]]</figure> | ||
| <figure id="uid3">[[File:seria2_5.png|150px|left]]</figure> | | <figure id="uid3">[[File:seria2_5.png|150px|left]]</figure> | ||
Wersja z 09:49, 19 maj 2015
Elektrodynamika dla Neuroinformatyki
Seria 2
Spis treści
Zadanie 1
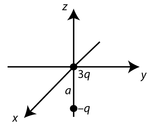
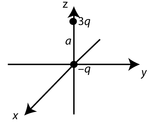
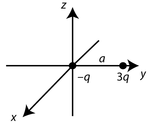
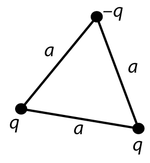
Dwa ładunki punktowe [math] 3q [/math] oraz [math] -q [/math] umieszczono w próżni w odległości [math] a [/math] od siebie. Dla każdego z układóww przedstawionych na poniższych rysunkach znaleźć moment monopolowy oraz dipolowy. Następnie znaleźć przybliżoną postać potencjału elektrycznego (we współrzędnych sferycznych) dla dużych odległości [math] \vec{r} [/math].
Zadanie 2
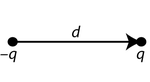
Znaleźć moment dipolowy dla dyskretnych układów ładunków przedstawionych na rysunkach. Sprawdzić, jak zmienia się wynik w zależności od wyboru początku układu współrzędnych.
Zadanie 3
Na cienkim pręcie, ułożonym wzdłuż osi [math] z [/math] i rozciągającym się od [math] z=-a [/math] do [math] z=+a [/math], umieszczono ładunek o podanej niżej gęstości liniowej. Dla każdego przypadku znaleźć wiodący człon rozwinięcia multipolowego dla potencjału.
- [math] \lambda = k \cos (\frac{\pi z}{2a}) [/math],
- [math] \lambda = k \sin (\frac{\pi z}{2a}) [/math],
- [math] \lambda = k \cos (\frac{\pi z}{a}) [/math],
gdzie [math] k [/math] jest pewną stałą.
Zadanie 4
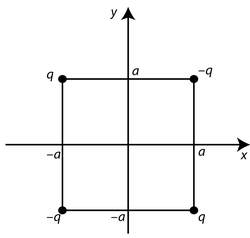
Znaleźć moment dipolowy oraz kwadrupolowy przedstawionego na rysunku układu ładunków. Czy i jak zmieni się wynik, jeśli przemieścimy układ współrzędnych o wektor [math] r\prime = [a , a , 0] [/math]? Jak w takiej sytuacji zachowa się moment dipolowy tego układu?
Zadanie 5
Znaleźć magnetyczny moment dipolowy dla prądu pochodzącego od poruszających się ładunków punktowych.
Zadanie 6
Znaleźć magnetyczny moment dipolowy płaskiego obwodu o polu powierzchni [math]S[/math], w którym płynie prąd o natężeniu [math] I [/math].