Laboratorium EEG/Analiza czas-częstość w matlabie: Różnice pomiędzy wersjami

Z Brain-wiki
Linia 206: Linia 206:
 
: <math> \Pi(t,f) =  \int_{-\infty}^{\infty}\int_{-\infty}^{\infty} f(\xi, \tau) e^{-i 2 \pi (f\tau + \xi t)} dt df</math>  
 
: <math> \Pi(t,f) =  \int_{-\infty}^{\infty}\int_{-\infty}^{\infty} f(\xi, \tau) e^{-i 2 \pi (f\tau + \xi t)} dt df</math>  
 
Najczęściej <math> \Pi</math>  wybiera się jako pewną funkcję gładzącą &mdash; w zależności od tego wyboru będziemy mieli w różnym stopniu osłabiane wyrazy mieszane.
 
Najczęściej <math> \Pi</math>  wybiera się jako pewną funkcję gładzącą &mdash; w zależności od tego wyboru będziemy mieli w różnym stopniu osłabiane wyrazy mieszane.
−
 
−
===MP &mdash; dopasowanie kroczące===
 
−
====Definicja====
 
−
Algorytm dopasowania kroczącego (ang. ''matching pursuit'', ''MP'') jest algorytmem iteracyjnie rozkładającym sygnał <math>s(t)</math> na funkcje bazowe (tzw. '''atomy czas-częstość''') <math>g_{\gamma_n}</math>  pochodzące ze zbioru <math>D</math> (zwanego '''słownikiem'''):
 
−
: <math>
 
−
\left \{
 
−
\begin{array}{l}
 
−
  R^0s =  s\\
 
−
  R^ns = \langle R^ns,g_{\gamma_n} \rangle g_{\gamma_n}+R^{n+1}s\\
 
−
  g_{\gamma_n} = \arg \max_{g_{\gamma_i} \in D } |\langle R^ns, g_{\gamma_i}\rangle|
 
−
\end{array}
 
−
\right .
 
−
</math>
 
−
gdzie:
 
−
<math>\arg \max_{g_{\gamma_i} \in D }</math> oznacza tego <math> g_{\gamma_i}</math>, który daje największy iloczyn skalarny z aktualnym residuum:  <math>|\langle R^ns, g_{\gamma_i}\rangle|</math>.
 
−
 
−
Słowniki mogą być dowolne, ale najczęściej składamy je z funkcji Diraca, sinus i Gabora:
 
−
: <math>
 
−
g_\gamma (t) = K(\gamma)e^{ -\pi\left( \frac{t-u}{\sigma} \right)^2}
 
−
\sin\left(2 \pi  f (t-u)+\phi\right)
 
−
</math>
 
−
normalizacja <math> K(\gamma)</math>  jest taka, że <math> ||g_{\gamma}||=1</math>, <math>\gamma=\{ u, f, \sigma,
 
−
\phi \}</math> to parametry funkcji w słowniku (<math>u</math> &mdash; translacja w czasie, <math> f</math> &mdash; częstość, <math> \sigma</math> &mdash; szerokość w czasie, <math> \phi</math> &mdash; faza).
 
−
 
−
====Dystrybucja energii====
 
−
Reprezentację czas-częstość uzyskujemy z dekompozycji MP sumując dystrybucje WVD pojedynczych atomów:
 
−
: <math>
 
−
W_{ g_{\gamma_n}}(t, f)=\int g_{\gamma_n} \bigl (t + \frac{\tau}{2} \bigr)\;
 
−
g_{\gamma_n}^*\left(t- \frac{\tau}{2} \right) e^{- i 2 \pi f \tau } d \tau
 
−
</math>
 
−
 
−
: <math>
 
−
E^{MP}  = \sum_{n=0}^M |\langle R^n s, \;g_{\gamma_n} \rangle|^2 \; W_{g_{\gamma_n}} (t, f)
 
−
</math>
 
−
 
−
W wyrażeniu tym nie ma wyrazów mieszanych :-)
 
  
 
==Krótkoczasowa transformacja Fouriera i spektrogram==
 
==Krótkoczasowa transformacja Fouriera i spektrogram==

Wersja z 14:08, 12 lut 2016

Laboratorium_EEG/Czas-częstość

Estymacja i analiza względnych zmian gęstości energii sygnału EEG w przestrzeni czas-częstość

Moduł czas-częstość w Matlabie

Zasada nieoznaczoności dla przestrzeni czas-częstość

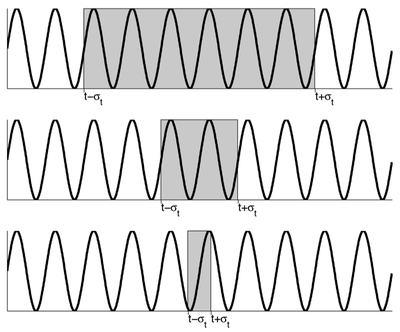
Poniższy rysunek obrazuje koncepcję zasady nieoznaczoności w przypadku analizy czas-częstość: im dokładniej znamy lokalizację interesującego nas fragmentu sygnału (struktury) w czasie tym mniej dokładnie możemy poznać jego częstość.

Zasada nieoznaczonosci tf.png

Zasadę tą można wyrazić formalnie w następujący sposób. Potraktujmy moc sygnału [math]x(t)[/math] (o skończonej energii) jak rozkład zmiennej losowej. Aby rozkład był unormowany trzeba podzielić go przez energię sygnału: [math]E_x = \int_{-\infty}^{\infty} |x(t)|^2 dt \lt \infty[/math]. Zatem rozkład ten jest postaci: [math]p(t) = \frac{1}{E_x}|x(t)|^2 [/math].

Jako lokalizację występowania sygnału w czasie przyjmujemy średnie położenie jego energii:

[math]t_0 = \frac{1}{E_x} \int_{-\infty}^{\infty}t |x(t)|^2 dt[/math]

zaś jako miarę skupienia energii wokół tego położenia przyjmujemy wariancję:

[math]\sigma_t^2 = \frac{1}{E_x}\int_{-\infty}^{\infty} (t - t_0)^2 |x(t)|^2 dt [/math]

Analogicznie w dziedzinie częstości:

[math]f_0 = \frac{1}{E_x} \int_{-\infty}^{\infty}f |X(f)|^2 df[/math]
[math]\sigma_f^2 = \frac{1}{E_x}\int_{-\infty}^{\infty} (f - f_0)^2 |X(f)|^2 df [/math]

Można pokazać (np. Pinsky, 2002), że iloczyn wariancji energii w czasie i w częstości jest ograniczony od dołu:

[math]\sigma_t^2 \sigma_f^2 \ge \frac{1}{16 \pi^2}[/math]

Estymatory gęstości widmowej dla przestrzeni czas-częstość

Energię sygnału w jednej z dziedzin, czasu bądź częstości, możemy policzyć tak:

[math] E_x=\int_{-\infty}^{\infty}{|x(t)|^2 dt} = \int_{-\infty}^{\infty}{|X(f)|^2 df}[/math]

i interpretujemy [math]|x(t)|^2[/math] albo [math]|X(f)|^2[/math] jako gęstości energii. Stąd pomysł, żeby rozszerzyć tą koncepcję na obie dziedziny jednocześnie i wprowadzić pojęcie gęstości energii w dziedzinie czas-częstość [math]\rho_x(t,f)[/math]:

[math] E_x=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}{\rho_x(t,f) dt df}[/math]

muszą też być spełnione własności brzegowe:

[math] \int_{-\infty}^{\infty}{\rho_x(t,f) dt}=|X(f)|^2[/math]
[math] \int_{-\infty}^{\infty}{\rho_x(t,f) df} = |x(t)|^2[/math]

Dystrybucja energii

Podobnie jak widmo mocy, gęstość energii fizycznego sygnału nie może być obliczona, może być jedynie estymowana. W celu estymacji gęstości energii można posłużyć się dwuwymiarowymi dystrybucjami energii. Jedną z podstawowych dystrybucji jest dystrybucja Wigner-Ville'a (WVD):

[math] W_x(t,f)=\int_{-\infty}^{\infty}x(t+\tau/2)x^*(t-\tau/2)e^{-i 2 \pi f \tau} d\tau[/math]

lub

[math] W_x(t,f) = \int_{-\infty}^{\infty} X(f+\xi/2)X^*(f-\xi/2) e^{i 2 \pi \xi t} d\xi[/math]

Implementacja

Przykładowa implementacja WVD dla sygnału rzeczywistego:

"wersja w matlabie" 

function [Tfr,ts,f]=tf_wvd(x,Fs,varargin)

doplot = true;
switch nargin
    case 0:1
        disp('tf_wvd - not enough input arguments');
        return
    case 2

    otherwise
        doplot=varargin{1};
end

x = hilbert(x);
samples = length(x);
N = floor(samples/2);
t = 0:samples; t(end)= [];
tfr = zeros(N,samples);
for ti=t
    for tau=0:min(ti,samples-ti)-1
        tfr(tau+1,ti+1) = x(ti+tau+1).*conj(x(ti-tau+1));
    end
end

Tfr = fft(tfr,samples,1);
ts = t./Fs;
f = linspace(0,Fs/2,N);

if doplot
    pcolor(linspace(0,ts(end),size(Tfr,2)),linspace(0,f(end),size(Tfr,1)),real(Tfr)); shading interp;
end

Własności

Własności WVD:

  • zachowanie energii
  • własności brzegowe
  • zachowywanie przesunięcia w czasie i w częstości
[math] y(t) = x(t-t_0) \Rightarrow W_y(t,f) = W_x(t-t_0,f)[/math]
[math] y(t) = x(t)e^{i 2 \pi f_0 t} \Rightarrow W_y(t,f) = W_x(t,f-f_0)[/math]
  • zachowywanie skalowania
[math] y(t)=\sqrt{k}x(kt) \Rightarrow W_y(t,f) = W_x(kt, f/k)[/math]

Wyrazy mieszane

WVD jest reprezentacją kwadratową więc:

[math] y(t) = x_1(t)+x_2(t) \Rightarrow W_y(t, f) = W_{x_1}(t, f)+W_{x_2}(t, f)+W_{x_1,x_2}(t, f)+W_{x_2,x_1}(t, f)[/math]

gdzie

[math] W_{x_1,x_2}(t, f) = \int_{-\infty}^{\infty} x_1(t+\tau/2)x_2^*(t-\tau/2)e^{-i 2 \pi f \tau} d\tau[/math]

Rozdzielczość

  • idealnie dla chirpów liniowych (sygnał o liniowo zmieniającej się częstości chwilowej):

Wersja w Matlabie 

Fs = 512.0;
T = 1.0;
t = tf_czas(T,Fs);
ch = tf_chirp(5,Fs/2-5,T,Fs);
[Tfr,ts,f] = tf_wvd(ch,Fs,false);
subplot(2,1,1)
plot(t,ch)
subplot(2,1,2)
pcolor(linspace(0,ts(end),size(Tfr,2)),linspace(0,f(end),size(Tfr,1)),real(Tfr)); shading interp;


  • struktura wyrazów mieszanych: zaobserwuj, że niezależnie od tego jak bardzo odseparowane są struktury w przestrzeni czas-częstość pomiędzy nimi powstają wyrazy mieszane. Zauważ, że wyrazy mieszane mają wysoką częstość przestrzennej zmienności.

Wersja w Matlabie 

Fs = 512.0;
T = 1.0;
t = tf_czas(T,Fs);
s1 = tf_gabor(0.3, 0.05, 1.0, 100, 0, Fs);
s2 = tf_gabor(0.7, 0.05, 1.0, 200, 0, Fs);
s = s1 + s2;
[Tfr,ts,f] = tf_wvd(s,Fs,false);
subplot(2,1,1)
plot(t,s)
subplot(2,1,2)
pcolor(linspace(0,ts(end),size(Tfr,2)),linspace(0,f(end),size(Tfr,1)),real(Tfr)); shading interp;


Klasa Cohena

WVD jest najprostszym elementem klasy Cohena. Ponieważ wyrazy mieszane mają wysoką częstość przestrzenną w płaszczyźnie czas-częstość to można je częściowo zniwelować poprzez zastosowanie odpowiedniego filtra. Koncepcja ta jest wykorzystywana w klasie Cohena. Ogólnie klasę tę można zapisać jako:

[math] C_x(t,f,\Pi) = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} \Pi(s-t, \xi - f) W_x(s,\xi) ds d\xi[/math]

gdzie

[math] \Pi(t,f) = \int_{-\infty}^{\infty}\int_{-\infty}^{\infty} f(\xi, \tau) e^{-i 2 \pi (f\tau + \xi t)} dt df[/math]

Najczęściej [math] \Pi[/math] wybiera się jako pewną funkcję gładzącą — w zależności od tego wyboru będziemy mieli w różnym stopniu osłabiane wyrazy mieszane.

Krótkoczasowa transformacja Fouriera i spektrogram

Definicja krótkoczasowej transformacji Fouriera

Krótkoczasowa transformacja Fouriera (ang. short-time Fourier transform, STFT) może być rozumiana jako seria transformacji Fouriera wykonanych na sygnale podzielonym na okienka, przy czym położenie okienka w czasie jest w ramach takiej serii przesuwane monotonicznie. W wersji ciągłej możemy to zapisać tak:

[math]F_x(t,f; h)= \int_{-\infty}^{\infty}{x(u) h^*(u-t)e^{- i 2 \pi u f} du} [/math]

Własności

Jeśli okienko ma skończoną energię to STFT jest transformacją odwracalną i można odzyskać z niej sygnał w reprezentacji czasowej:

[math] x(t) = \frac{1}{E_h}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}F_x(u,f;h)h(t-u)e^{i 2\pi t f}\,du\,df [/math]

gdzie [math]E_h=\int_{-\infty}^{\infty}|h(t)|^2\,dt [/math] Tak więc sygnał może być rozłożony na liniową kombinację elementarnych falek-„atomów” postaci:

[math]h_{t,f}(u)=h(u-t)e^{i 2 \pi f u}[/math]

Każdy atom uzyskiwany jest przez translację pojedynczego okna [math]h[/math] w czasie i jego modulację częstością [math]f[/math].

Spektrogram

Definicja

Spektrogram: kwadrat modułu STFT jest estymatą gęstości energii w przestrzeni czas-częstość:

[math]S_x(t, f) =\left|\int_{-\infty}^{\infty}{x(u) h^*(u - t) e^{-i 2\pi f u} du}\right|^2[/math]

Implementacja

  • Spektrogram zaiplementowany jest w pythonie w module matplotlib.pyplot jako funkcja specgram (dokumentacja).
  • W matlabie spectrogram jest zaimplementowany w signal procesing toolbox:

dokumentacja

Własności

Przesunięcia

Spektrogram zachowuje przesunięcie:

w czasie

[math]y(t) = x(t - t_0)\Rightarrow S_y(t, f; h) = S_x(t - t_0, f; h)[/math]

Wersja w Matlabie 

% parametry
t0    = 1.0;
sigma = 0.1;
T     = 4.0;
f     = 10;
phi   = 0;
Fs    = 128.0;
NFFT  = floor(Fs);
 
sig1 = tf_gabor(t0, sigma, T, f, phi, Fs); 
        % sygnał
sig2 = tf_gabor(t0 + 2, sigma, T, f, phi, Fs); 
        % sygnał przesunięty w czasie
 
subplot(2,2,1);
sig1_padded = [zeros(1,floor(NFFT/2)), sig1, zeros(1,floor(NFFT/2))];
P=spectrogram(sig1_padded,NFFT,NFFT-1,NFFT,Fs);
pcolor(linspace(0,T,size(P,2)),linspace(0,Fs/2,size(P,1)),abs(P)); shading interp;

subplot(2,2,2)
sig2_padded = [zeros(1,floor(NFFT/2)), sig2, zeros(1,floor(NFFT/2))];
P=spectrogram(sig2_padded,NFFT,NFFT-1,NFFT,Fs);
pcolor(linspace(0,T,size(P,2)),linspace(0,Fs/2,size(P,1)),abs(P)); shading interp;

subplot(2,2,3)
time    = tf_czas(T, Fs);
plot(time,sig1);
  
subplot(2,2,4)
plot(time ,sig2);


i w częstości:

[math]y(t) = x(t) e ^{i 2 \pi f_0 t}\Rightarrow S_y(t, f; h) = S_x(t, f - f_0; h)[/math]

Wersja w Matlabie 

% parametry
t0    = 1.0;
sigma = 0.1;
T     = 4.0;
f     = 10;
phi   = 0;
Fs    = 128.0;
NFFT  = floor(Fs);
time    = tf_czas(T, Fs);
sig1 = tf_gabor(t0, sigma, T, f, phi, Fs); 
        % sygnał
sig2 = tf_gabor(t0, sigma, T, f+20, phi, Fs);
        % sygnał przesunięty w częstości
 
subplot(2,2,1);
sig1_padded = [zeros(1,floor(NFFT/2)),sig1,zeros(1,floor(NFFT/2))];
P=spectrogram(sig1_padded,NFFT,NFFT-1,NFFT,Fs);
pcolor(linspace(0,T,size(P,2)),linspace(0,Fs/2,size(P,1)),abs(P)); shading interp;
 
subplot(2,2,2)
sig2_padded = [zeros(1,floor(NFFT/2)),sig2,zeros(1,floor(NFFT/2))];
P=spectrogram(sig2_padded,NFFT,NFFT-1,NFFT,Fs);
pcolor(linspace(0,T,size(P,2)),linspace(0,Fs/2,size(P,1)),abs(P)); shading interp;
 
subplot(2,2,3)
plot(time,sig1);
 
subplot(2,2,4)
plot(time ,sig2);


Wyrazy mieszane

Spektrogram jest reprezentacją kwadratową. Spektrogram sumy sygnałów nie jest sumą spektrogramów sygnałów składowych, jest tam jeszcze coś:

[math]y(t) = x_1(t)+x_2(t) \Rightarrow S_y(t, f) = S_{x_1}(t, f)+S_{x_2}(t, f)+S_{x_1,x_2}(t, f)+S_{x_2,x_1}(t, f)[/math]

gdzie

[math]S_{x_1,x_2}(t, f) = F_{x_1}(t, f)F^*_{x_2}(t, f)[/math]

Jak mogą wyglądać wyrazy mieszane ilustruje poniższy kod. Kolejne subploty pokazują spektrogramy uzyskane dla sygnału będącego sumą dwóch funkcji Gabora o częstościach różniących się o 2 Hz i położeniach różniących się o kolejne wielokrotności 0,1 s.

Wersja w Matlabie 

% parametry
t0    = 1.0;
sigma = 0.05;
T     = 2.0;
f0    = 20;
phi   = 0;
Fs    = 128.0;
NFFT  = floor(Fs);
time  = tf_czas(T, Fs);
 
for i=0:8
    subplot(3,3,i+1)
    sig1  = tf_gabor(t0, sigma, T, f0, phi, Fs); % sygnal
    sig2  = tf_gabor(t0+i*0.1, sigma, T, f0+2, phi, Fs);
        % sygnał przesunięty w częstości o 2 Hz i w czasie o i*0.1 s
    sig1_padded = [zeros(1,floor(NFFT/2)),sig1,zeros(1,floor(NFFT/2))];
    sig2_padded = [zeros(1,floor(NFFT/2)),sig2,zeros(1,floor(NFFT/2))];
    P=spectrogram(sig1_padded+sig2_padded,NFFT,NFFT-1,NFFT,Fs);
    pcolor(linspace(0,T,size(P,2)),linspace(0,Fs/2,size(P,1)),abs(P)); shading interp;
end


Wyrazy mieszane występują także w przypadku pojedynczej struktury dla sygnału rzeczywistego. „Mieszające się” obiekty to energia zlokalizowana w dodatniej i ujemnej części widma częstości. Efekt jest stosunkowo słaby i uwidacznia się dopiero na mapach czas-częstość logarytmu gęstości energii. Problem ten można obejść stosując transformację Hilberta, gdyż po tej transformacji cała energia skupiona jest w dodatniej części widma. Własność tę ilustruje poniższy program:


Wersja w Matlabie 

% parametry
t0    = 0.5;
sigma = 0.1;
T     = 1.0;
f     = 30;
phi   = 0;
Fs    = 256.0;
NFFT  = 32;
Fs2   = floor(Fs/2);
 
s = tf_gabor(t0, sigma, T, f, phi, Fs);
t = tf_czas(T, Fs);
f = linspace(-Fs2,Fs2,NFFT+1); f(end) = [];
 
subplot(4,1,1)
plot(t,s);
 
subplot(4,1,2)
P=spectrogram(s,NFFT,NFFT-1,f,Fs);
pcolor(linspace(0,T,size(P,2)),linspace(f(1),f(end),size(P,1)),abs(P)); shading interp;
 
subplot(4,1,3)
pcolor(linspace(0,T,size(P,2)),linspace(f(1),f(end),size(P,1)),log(abs(P))); shading interp;
 
subplot(4,1,4)
s_ana = hilbert(s); % sygnał analityczny
P=spectrogram(s_ana,NFFT,NFFT-1,f,Fs);
pcolor(linspace(0,T,size(P,2)),linspace(f(1),f(end),size(P,1)),log(abs(P))); shading interp;

Ćwiczenie:

  • Proszę zbadać rozdzielczość czasową spektrogramu posługując się funkcją delta oraz rozdzielczość częstotliwościową posługując się funkcją sinus (Trzeba „przeskanować” czas funkcją delta, a częstości sinusem). Proszę wykonać to dla kilku długości okienek h.
  • Proszę zbadać rozdzielczość spektrogramu przy pomocy dwóch funkcji Gabora, dla różnych ich odległości w czasie i w częstości. Zaobserwować strukturę wyrazów mieszanych.


Ciągła transformata falkowa i skalogram

Ciągłą transformata falkowa

Definicja

Ciągła transformacja falkowa (ang. Continuous Wavelet Transform, CWT) dana jest wzorem:

[math] P_x(t,a;\Psi)= \int_{-\infty}^{\infty}{x(s)\Psi^*_{t,a}(s) ds}[/math]

gdzie

[math] \Psi_{t,a}(s) = \frac{1}{\sqrt{|a|}} \Psi\left(\frac{s-t}{a}\right)[/math]

a jest skalą. Od falki [math]\Psi[/math] wymagamy żeby miała średnią 0.

Transformację tę można interpretować jako rzutowanie sygnału na kolejne wersje falki [math]\Psi[/math] przesunięte o t i przeskalowane o a.

Inne spojrzenie na transformację falkową uwidacznia się gdy połączymy dwa powyższe wzory:

[math]P_x(t,a;\Psi)= \frac{1}{\sqrt{|a|}}\int_{-\infty}^{\infty}{x(s) \Psi^*\left(\frac{s-t}{a}\right) ds} [/math]

Tu widać, że dla ustalonej skali a transformacja falkowa jest splotem sygnału z falką o skali a. Ten sposób myślenia o transformacji falkowej umożliwia zastosowanie szybkiego algorytmu obliczeniowego bazującego na tym, że splot w dziedzinie czasu odpowiada mnożeniu w dziedzinie częstości.

Skalogram

Podobnie jak dla STFT i spektrogramu, możemy dla CWT wprowadzić pojęcie skalogramu, będącego estymatą gęstości energii w przestrzeni czas-skala.

[math]S_x(t,a;\Psi)=\left| P_x(t,a;\Psi)\right|^2[/math]

Dla falek, które są dobrze skupione wokół częstości [math]f_0[/math] dla skali [math]a_0=1[/math] można wprowadzić utożsamienie [math]f=\frac{f_0}{a}[/math]. Utożsamienie to pozwala przekształcić reprezentację czas-skala w reprezentację czas-częstość:

[math]S_x(t,f;\Psi)=\left| P_x(t,f_0/f;\Psi)\right|^2[/math]

Implementacja

Przykładowa implementacja obliczania skalogramu dla falek Morleta przedstawiona jest poniżej. Korzysta ona z własności splotu.

Wersja w Matlabie 

function [P,f,t]=tf_cwt(x,MinF,MaxF,Fs,varargin)

w = 7;
df = 1;
doplot = true;
switch nargin
    case 0:3
        disp('tf_cwt - not enough input arguments');
        return
    case 4

    case 5
        w=varargin{1};
    case 2
        w=varargin{1};
        df=varargin{2};
    otherwise
        w=varargin{1};
        df=varargin{2};
        doplot=varargin{3};
end

T = length(x)/Fs;
M = length(x);
t = 0:1/Fs:T; t(end) = [];
freqs = MinF:df:MaxF; freqs(end) = [];
P = zeros(length(freqs),M);
X = fft(x);

for i=1:length(freqs)
    f = freqs(i);
    s = T*f/(2*w);
    psi = fft(tf_morlet(M,w,s,true));
    psi = psi./sqrt(sum(abs(psi).^2));
    tmp = fftshift(ifft(X.*psi));
    P(i,:) = abs(tmp).^2;
end

if doplot
    pcolor(linspace(0,T,size(P,2)),linspace(MinF,MaxF,size(P,1)),P); shading interp;
end

Matching pursuit

Dopasowanie kroczące (ang. matching pursuit, MP) jest procedurą polegającą na rozłożeniu sygnału na funkcje składowe pochodzące z określonego zbioru funkcji (słownika). Słowniki wykorzystywane w metodach czas-częstość często składają się z funkcji Gabora tj. funkcji sinus modulowanej funkcją Gaussa. MP jest algorytmem iteracyjnym. W pierwszym kroku wybierana jest funkcja dająca największy iloczyn skalarny z sygnałem. W każdym następnym kroku funkcja jest analogicznie dopasowywana do residuum sygnału, pozostałego po odjęciu wyniku poprzedniej iteracji.

Ćwiczenia

Zadanie 1

  • Zapoznać się z opisem metod czas-częstość, wykonując polecenia opisane przy każdej z metod.
  • Zbadać własności metod czas-częstość, m.in.:
    • Proszę przyjrzeć się definicjom transformaty falkowej i STFT i opowiedzieć o analogiach i różnicach.
    • Proszę zbadać własności przesunięć w czasie i w częstości dla skalogramu w sposób analogiczny jak było to pokazane dla spektrogramu.
    • Proszę zbadać strukturę wyrazów mieszanych w sposób analogiczny jak było to pokazane dla spektrogramu.

Zadanie 2

Zbadaj działanie algorytmu MP na samodzielnie wytworzonych sygnałach symulowanych:

  • Trzech funkcjach Gabora o różnych częstościach, amplitudach i położeniach w czasie i o podobnej rozciągłości w czasie tak, aby zasadniczo nie nachodziły na siebie (patrz rysunek). Wykonaj dopasowanie dla trzech atomów, narysuj sygnał oryginalny i nałożony na niego sygnał zrekonstruowany z wyliczonych atomów, różnicę tych sygnałów (residuum) oraz mapę czas-częstość.
Eeglab gabory3.png
  • Dwóch jednakowych funkcji Gabora położonych w pewnej odległości od siebie w czasie. Zbadaj jakość dopasowania dokonując rekonstrukcji dwoma i trzema atomami na rysunkach podobnych jak w poprzedniej części zadania. Sprawdź co się dzieje przy zwiększaniu odległości w czasie pomiędzy tymi funkcjami Gabora.
Eeglab gabory2.png

Eeglab gabory2 dalej.png

Zadanie 3

Korzystając z danych SSVEP zebranych podczas zajęć w semestrze zimowym:

  • Uśrednić odcinki sygnałów zbierane dla tych samych częstości stymulacji, zostawiając przed i po sygnale okres referencyjny (np. 2 s).
  • Wykonać mapy czas-częstość za pomocą spektrogramu, korzystając z reprezentacji falek Morleta i Wignera-Villa.
  • Wykonać analizę czas-częstość posługując się pakietem EEGLAB.

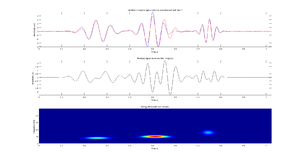
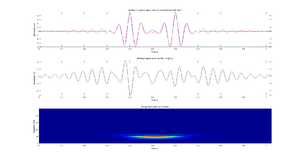
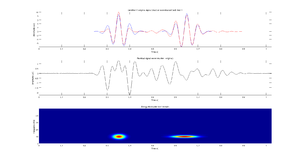
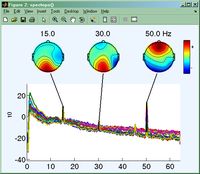
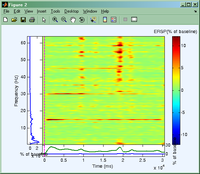
Rysunki poniżej przedstawiają przykład analizy danych EEG zebranych podczas stymulacji SSVEP o częstości 15 Hz.

Eeglab ssvep1.png

Eeglab ssvep2.png

Zadanie 4

Pobrać plik z danymi: https://brain.fuw.edu.pl/~suffa/LabEEG/Characterize_ch4_F50_G4.mat

Opis danych: dane zawierają zapisy z lokalnych potencjałów polowych (LFP) z kory czuciowej małpy podczas podawania bodźca wibracyjnego do palca. Macierz zawiera 50 powtórzeń po 3 sekundy. Częstość próbkowania wynosi 5000 Hz. Bodziec podawany był pomiędzy 1 a 2 sekundą.

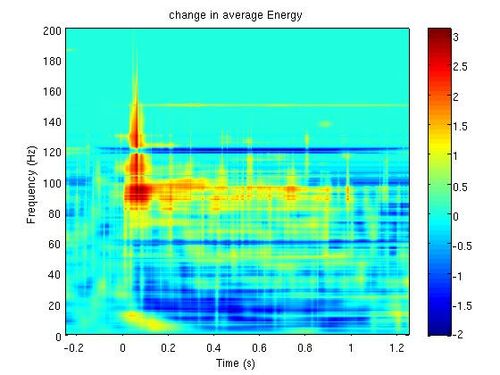
Analiza zapisów LFP z kory czuciowej małpy podczas podawania bodźca wibracyjnego do palca, o częstości 50 Hz. Mapa czas-częstość przedstawia względną gęstość energii (w skali dB) względem okresu referencyjnego 200-50 ms przed początkiem stymulacji. Dane opisane są w pracy: Supratim Ray, Steven S. Hsiao, Nathan E. Crone, Piotr J. Franaszczuk, and Ernst Niebur. Effect of Stimulus Intensity on the Spike—Local Field Potential Relationship in the Secondary Somatosensory Cortex. The Journal of Neuroscience, 2008, 28(29):7334-7343.

Zadania do wykonania:

  • Otrzymać mapy czas-częstość dla pojedynczych realizacji a następnie uśrednić je po realizacjach.
  • Na średniej mapie poszukać występowania odpowiedzi w częstościach high-gamma (100-200 Hz).
  • W przypadku braku widocznej odpowiedzi, rozważyć następujące operacje:
    • usunąć częstości sieci (60 Hz i wyższe harmoniczne);
    • zastosować logarytmiczną skalę energii;
    • policzyć zmiany gęstości energii względem jej wartości w okresie referencyjnym.

Mapa czas-częstość średniej gęstości energii otrzymaną metodą Matching Pursuit jest przedstawiona na rys. 1.

Zadanie 5

Wykonać analizę metodą MP dla danych z zadania 3.

Problem wyboru optymalnego estymatora gęstości energii w przestrzeni czas-częstość dla sygnałów EEG

Dwa aspekty, które trzeba wziąć pod uwagę w praktyce analizy sygnałów EEG to:

  • rozdzielczość czas-częstość oferowaną przez daną metodę;
  • łatwość interpretacji wyników dla sygnałów złożonych z wielu, a priori nieznanych struktur — takim niezwykle złożonym sygnałem jest EEG.

Jeśli chodzi o rozdzielczość czasowo-częstościową estymatorów gęstości energii sygnałów to wiadomo, że jest ona ograniczona przez zasadę nieoznaczoności Heisenberga w analizie sygnałów.

Minimum iloczynu wariancji w dziedzinie czasu i wariancji w dziedzinie częstości, osiągane jest przez dystrybucję Wigner-Villa dla sygnału będącego funkcją Gabora. Dystrybucja Wigner-Villa jest formą kwadratową. W przypadku bardziej złożonych sygnałów własność ta prowadzi do powstawania wyrazów mieszanych, które utrudniają prawidłową interpretację wyników. Dystrybucje wywodzące się z dystrybucji Wigner-Villa tworzą klasę dystrybucji Cohena. W klasie tych dystrybucji do tłumienia wyrazów mieszanych stosowane jest jądro, będące efektywnie czasowo-częstościowym filtrem dolnoprzepustowym. Często stosowanym w czasowo-częstościowej analizie sygnałów reprezentantem klasy dystrybucji Cohena jest dystrybucja Choi-Williamsa, gdzie jądrem filtru jest dwuwymiarowa funkcja Gaussa. Odpowiedni dobór własności jądra umożliwia stłumienie niektórych wyrazów mieszanych --- metoda ta może być szczególnie efektywna jeśli znane są \emph{a priori} czasowo-częstościowe własności struktur obecnych w sygnale. Należy także pamiętać, że filtrowanie prowadzi do zmniejszenia rozdzielczości czas-częstość. Alternatywą dla dystrybucji czas-częstość są metody oparte o liniowe reprezentacje czas-częstość takie jak krótkoczasowa transformata Fouriera (spektrogram) czy transformata falkowa (skalogram). W metodach tych sygnał analizowany jest przy pomocy funkcji zlokalizowanych w czasie i częstości. Zastosowanie funkcji zlokalizowanych częściowo zmniejsza problem wyrazów mieszanych, jednak ich rozdzielczość czas-częstość jest związana z rozciągłością czasowo-częstościową stosowanych funkcji. Metody te nie zapewniają dopasowania do struktur obecnych w sygnale.

W pracy {\bf H1} zademonstrowano, że najbardziej optymalne dla analizy sygnałów EEG własności posiada metoda oparta o dekompozycję sygnału algorytmem Matching Pursuit (MP). Ten estymator gęstości energii konstruowany jest jako suma dystrybucji Wigner-Villa poszczególnych składowych wyodrębnionych z sygnału w trakcie dekompozycji. W sposób wynikający bezpośrednio z konstrukcji, estymator ten nie posiada wyrazów mieszanych oferując jednocześnie najwyższą możliwą rozdzielczość czasowo-częstościową. Kompromis pomiędzy rozdzielczością w czasie a rozdzielczością w częstości jest w każdej iteracji algorytmu MP optymalizowany ze względu na struktury występujące w sygnale. W tym sensie metoda ta jest lokalnie adaptywną reprezentacją czas-częstość, w odróżnieniu od krótkoczasowej transformaty Fouriera czy transformat falkowych.


Klasyczna technika pomiaru efektów ERD/ERS opisana w sekcji \ref{sect:ERDS_klasycznie} bazuje na uśrednianiu energii sygnałów przefiltrowanych w wybranym paśmie częstości. Wymaga ona wyboru \emph{reaktywnych} (dających największe zmiany mocy) pasm częstości. Pasm takich zwykle poszukiwano metodą prób i błędów. Ze względu na dużą zmienność osobniczą pasm reaktywnych, znacznie lepszym podejściem, które umożliwia całościowe spojrzenie na efekty modyfikacji widma mocy sygnału EEG, jest analiza czasowo-częstościowa. Polega ona na estymowaniu gęstości energii w przestrzeni czas-częstość dla każdego powtórzenia osobno. Następnie dla każdej częstości, obliczana jest miara ERD/ERS, przy pomocy równania \eqref{eq:ERD_klasyczny}. W efekcie uzyskiwana jest mapa prezentująca zjawiska ERD/ERS w przestrzeni czas-częstość.

Najczęściej stosowanymi do szacowania ERD/ERS estymatorami gęstości energii są: spektrogram \citep{Makeig_1993}, skalogram \citep{Tallon_1996}, dystrybucje klasy Cohena \citep{Lachaux_2000} lub filtrowanie pasmowe w zachodzących na siebie pasmach częstości \citep{Graimann_2002}. W sytuacjach gdy istotna jest wysoka rozdzielczość czasowo-częstościowa zaproponowana została metoda Matching Pursuit \citep{Durka_2001}. Raportowane wyniki zależą w pewnym stopniu od własności sygnału, ale również w pewnym stopniu od zastosowanego estymatora i jego parametrów.

Prace innych autorów zwykle skupiały się na zastosowaniach jednego konkretnego estymatora. Nie dyskutowano w nich jaki wpływ na identyfikację efektów reakcji na bodziec ma wybór metody estymacji gęstości energii. Problem ten został zbadany w pracach {\bf H2} i {\bf H3}. Wszystkie badane estymatory zostały zastosowane do tych samych zestawów danych co umożliwiło praktyczne porównanie wpływu estymatora na czytelność i jednoznaczność wyników. W pracy {\bf H2} pokazano, że algorytm MP daje estymaty o wyższej rozdzielczości niż spektrogram, niemniej w kontekście identyfikacji obszarów przestrzeni czas-częstość, w których przejawia się reakcja związana z bodźcem, wyniki otrzymane przy pomocy obu estymatorów są podobne i spójne. W pracy {\bf H3} zagadnienie badania optymalności estymatora zostało rozszerzone w dwóch aspektach. Do porównania włączono skalogram zaś porównanie metod przeprowadzono zarówno dla danych EEG jak i ECoG. Wykazane zostało, że wszystkie wymienione powyżej metody estymacji gęstości energii w dziedzinie czas-częstość dają spójne wyniki. Wykazano, że estymator oparty o dekompozycję MP umożliwia badanie mikrostruktury zmian gęstości energii dzięki najwyższej rozdzielczości czas-częstość. Jednocześnie, dzięki lokalnie adaptywnemu kompromisowi pomiędzy rozdzielczością w czasie a rozdzielczością w częstości daje on wyniki, w których eksponowana jest struktura sygnału nie obarczona w sposób systematyczny własnościami rozdzielczości czasowo-częstościowej metody. W przypadku pozostałych metod, przy interpretacji otrzymanych map czas-częstość należy brać pod uwagę specyficzną dla danej metody strukturę wyrazów mieszanych i zależność pomiędzy rozdzielczością w czasie a rozdzielczością w częstości (porównaj {\bf H3}, Rys.\,3).

Problem istotności statystycznej efektów ERD i ERS w przestrzeni czas-częstość

W badaniach naukowych bardzo ważnym elementem jest ocena istotności statystycznej obserwowanych zjawisk. Dążeniem naszym jest aby identyfikowane zmiany mocy sygnału był efektem związanym z bodźcem, a nie jedynie artefaktem fluktuacji statystycznych. Problem prawidłowej oceny istotności statystycznej zmian w rozkładach gęstości energii w dziedzinie czas-częstość został opisany w serii dwóch artykułów {\bf H2} i {\bf H3}. Zaproponowane rozwiązanie opiera się na masowym zastosowaniu testów jednowymiarowych i korygowaniu wyników uwzględniając wielokrotność testowania. Zbadano dwa zagadnienia: \begin{itemize} \item wybór statystyki \item rodzaj korekty poziomu istotności testów ze względu na wielokrotność porównań. \end{itemize}


Wcześniejsze prace innych autorów nie wskazywały poprawnego metodologicznie rozwiązania zagadnienia wielokrotnych porównań, które stanowi tu główny problem. Przykładowo \citet{Makeig_1993} jako rozwiązanie problemu wielokrotnych porównań proponuje przyjęcie poziomu istotności pojedynczego testu jako 0.001. W pracy \citet{Lachaux_2000} istotność wzrostu mocy była szacowana dla pojedynczego pasma częstości, problem wielokrotnych porównań był wspomniany, ale nie rozwiązany w przypadku porównywania aktywności wielu pasmach jednocześnie. W pracy \citep{Graimann_2002} szacowano istotność statystyczną w poszczególnych pasmach niezależnie, a następnie prezentowano mapę stworzoną z tych pasm nie korygując poziomów istotności.

Przyczyny takiego stanu rzeczy można upatrywać w fakcie, że powszechnie stosowaną poprawką na poziom błędu I rodzaju ze względu na wielokrotność porównań jest poprawka Bonferroniego. Poprawka ta daje prawidłową korektę poziomu istotności dla testów niezależnych. W przypadku testów skorelowanych poprawka ta jest zbyt konserwatywna. W analizie czasowo-częstościowej mamy do czynienia z bardzo dużą ilością testów, które są ze sobą skorelowane w \emph{a priori} nieznanym stopniu. Zastosowanie tu poprawki Bonferroniego prowadzi do testów skrajnie konserwatywnych. Jako rozwiązanie tego problemu w pracy {\bf H2} została zaproponowana rezygnacja z kontroli błędu I rodzaju na rzecz kontroli frakcji fałszywych odkryć (false discovery rate, FDR) \citep{FDR}. W kolejnych paragrafach omówione zostaną istotne elementy rozwiązań zaproponowanych w pracach {\bf H2} i {\bf H3}.

Podział przestrzeni czas-częstość.

W pracy {\bf H2} stwierdzono, że aby móc wygodnie sformułować hipotezy i poddać je testom należy podzielić przestrzeń czas-częstość na elementy rozdzielczościowe (ang. resolution element---\emph{resel}). Iloczyn rozciągłości czasowej i częstościowej jest od dołu ograniczony przez zasadę nieoznaczoności. W praktyce, co zostało zbadane w pracy {\bf H2}, rozmiar resela musi być większy ze względu na wariancję estymatorów i wariancję danych pomiędzy realizacjami.

\paragraph{Hipotezy.} Stosując opisany powyżej podział przestrzeni czas-częstość na resele można sformułować następującą rodzinę hipotez: dla każdego resela hipoteza zerowa stwierdza, że średnia energia rozważanego resela równa jest średniej energii reseli o tej samej częstości należących do okresu referencyjnego, hipoteza alternatywna stwierdza, że średnia energia w okresie referencyjnym i w rozważanym reselu są różne. Uśrednianie przebiega po realizacjach.

Wybór statystyki.

W pracy {\bf H2} zademonstrowano, że rozkłady energii w reselach są zależne od zastosowanego estymatora gęstości energii, ale w większości przypadków są dalekie od rozkładów normalnych. Wykazano, że zastosowanie intensywnych obliczeniowo testów nieparametrycznych prowadzi do poprawnych i nieobciążonych wyników. Spośród dwóch zbadanych testów bardziej efektywnym okazał się test oparty na estymowaniu empirycznego rozkładu statystyki pseudo-t w okresie referencyjnym.

W pracy {\bf H3} wykazano, że w wielu praktycznych przypadkach poprawne rezultaty można uzyskać stosując odpowiednio testy parametryczne. Pierwszym koniecznym krokiem jest normalizacja danych, czyli poddanie energii reseli takiej transformacji, że rozkład otrzymanych danych jest dobrze przybliżony rozkładem normalnym. Zaproponowano w tym celu zastosowanie transformacji Boxa-Coxa \citep{boxcox}. Kolejną cechą rozważanych testów jest niejednorodność wariancji w okresie referencyjnym i pobodźcowym. Teoretycznym rozwiązaniem tego problemu jest test $t$ ze zmodyfikowaną ilością stopni swobody zgodnie z poprawką Welcha \citep{welch}. W pracy {\bf H3} pokazano, że dla danych testowych zarówno EEG (Rys. 1) jak i ECoG (Rys. 2) standardowy test $t$ jak i test $t$ z poprawką Welcha daje wyniki niemal identyczne z testem nieparametrycznym zaproponowanym w {\bf H2}. Zastosowanie testów parametrycznych znacząco redukuje złożoność obliczeniową problemu oceny istotności statystycznej zmian mocy sygnału w dziedzinie czas-częstość.


Problem wielokrotnych porównań.

Ocena istotności statystycznej dla wszystkich analizowanych reseli w dziedzinie czas-częstość prowadzi w naturalny sposób do powstania problemu wielokrotnych porównań. Jak wspomniano we wstępie do tej sekcji, we wcześniejszych pracach dotyczących analizy odpowiedzi fazowo nie związanej z bodźcem w dziedzinie czas-częstość nie zaproponowano poprawnego rozwiązania problemu wielokrotnych porównań. W pracy {\bf H2} jako efektywne i ścisłe rozwiązanie problemu wielokrotnych porównań została zaproponowana metoda kontroli frakcji fałszywych odkryć \citep{FDR} (false discovery rate, FDR). Rozważono założenia i porównano wyniki otrzymywane dla klasycznej metody kontrolowania błędu I rodzaju dla problemu wielokrotnych porównań Bonferroniego-Holmsa z metodą opartą o kontrolę FDR. Aby praktycznie zilustrować efektywność i skuteczność metody kontroli błędów w oparciu o podejście FDR zaprojektowano i przeprowadzono eksperyment, w którym celowo wydłużono czas rejestracji sygnału EEG, tak aby zawierał on znaczący udział zapisu spoczynkowego, w którym \emph{a priori} nie powinny występować efekty związane z bodźcem. Otrzymano poprawną kontrolę ilości fałszywych detekcji zachowując jednocześnie moc testów wystarczającą do potwierdzenia istotności znanych efektów ERD/ERS. Ilustracją tego wyniku są Rys. 4 i 5 z pracy {\bf H2}. Z przedstawionych w pracy {\bf H2} wyników wyciągnięto wniosek, że w przypadku wielokrotnych testów wykonywanych dla reseli w dziedzinie czas-częstość procedura Bonferroniego-Holmsa jest zbyt konserwatywna, natomiast procedura FDR zachowuje wystarczającą moc aby być w praktyce przydatną.

Literatura

S. Mallat and Z. Zhang (1993) Matching pursuit with time-frequency dictionaries. IEEE Transactions on Signal Processing, 41:3397-3415.

Pinsky, Mark (2002), Introduction to Fourier Analysis and Wavelets, Brooks/Cole, ISBN 0-534-37660-6


Laboratorium_EEG/Czas-częstość

Źródło: „http://brain.fuw.edu.pl/edu/index.php?title=Laboratorium_EEG/Analiza_czas-częstość_w_matlabie&oldid=4712”