USG/Doppler: Różnice pomiędzy wersjami
| (Nie pokazano 15 wersji utworzonych przez 2 użytkowników) | |||
| Linia 1: | Linia 1: | ||
| − | =Metoda dopplerowska= | + | =Metoda dopplerowska impulsowa (Pulsed Wave)= |
| − | Do dyspozycji mamy zestaw zrekonstruowanych danych RF z 64 kolejnych nadań pod stałym kątem (zerowym) falą płaską o parametrach: | + | Do dyspozycji mamy zestaw zrekonstruowanych danych RF ([http://www.fuw.edu.pl/~jarekz/FUW-FID-2016/raw-data/usg3_doppler_circle_10lh.npy link]) z 64 kolejnych nadań pod stałym kątem (zerowym) falą płaską o parametrach: |
| + | |||
<source lang = python> | <source lang = python> | ||
| − | f0 = | + | f0 = 5.5e6 # Częstotliwość nadawcza [Hz] |
| − | z_step = | + | z_step = 3.079291762894534e-05 # Odległość między kolejnymi punktami w głębokości na siatce rekonstruowanego obrazu [m] |
| − | T_PRF = 1./ | + | PRF = 1000 # Pulse Repetition Frequency [Hz] |
| + | T_PRF = 1./PRF # czas między kolejnymi nadaniami [s] | ||
</source> | </source> | ||
| Linia 14: | Linia 16: | ||
==Demodulacja sygnału RF== | ==Demodulacja sygnału RF== | ||
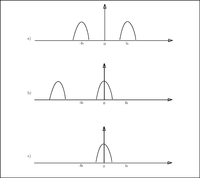
| − | Estymator autokorelacyjny stosowany jest zdemodulowanym sygnale | + | Estymator autokorelacyjny stosowany jest na zdemodulowanym sygnale kwadraturowym I/Q (ang. In-Phase/Quadrature). Sygnał RF rejestrowany bezpośrednio z przetworników odbiorczych jest sygnałem rzeczywistym (zerowa część urojona) o pasmowej charakterystyce widmowej. Informacja istotna z naszego punktu widzenia położona jest w paśmie, którego środek znajduje się częstotliwości nadawczej; szerokość tego pasma zależna jest od fizycznych właściwości głowicy ultradźwiękowej i nazywana jest pasmem przenoszenia głowicy. Demodulacja jest operacją pozwalającą na przekształcenie takiego sygnału w sygnał zespolony o paśmie położonym wokół częstotliwości zerowej. Taki zabieg pozwala na zmniejszenie częstotliwości próbkowania - potencjalnie poniżej częstotliwości Nyquista określonej dla składowych sygnału niezdemodulowanego. |
| − | [[Plik:Rys_demodulation.png|200px|thumb|right|Widmo sygnału: a) przed demodulacją; b) po demodulacji; c)po demodulacji i filtrowaniu.]] | + | [[Plik:Rys_demodulation.png|200px|thumb|right|Widmo sygnału: a) przed demodulacją; b) po demodulacji; c) po demodulacji i filtrowaniu.]] |
| + | |||
Demodulację możemy przeprowadzić zarówno na danych surowych RF, jak i na danych po rekonstrukcji. W naszym wypadku zastosujemy to drugie rozwiązanie. | Demodulację możemy przeprowadzić zarówno na danych surowych RF, jak i na danych po rekonstrukcji. W naszym wypadku zastosujemy to drugie rozwiązanie. | ||
| − | + | ||
| − | Na początku stworzymy funkcję dokonującą demodulacji każdego z obrazów, tj. dla | + | Na początku stworzymy funkcję dokonującą demodulacji każdego z obrazów, tj. dla każdej próbki o współrzędnych <math>(x,y)</math> |
| − | <math>IQ(x,y)=RF(x,y)\cdot e^{-i\cdot2\pi f_{0}t} </math> | + | |
| + | <math>IQ(x,y)=RF(x,y)\cdot e^{-i\cdot2\pi f_{0}t} </math> | ||
| + | |||
gdzie <math>IQ</math> - sygnał po demodulacji; <math>RF</math> - sygnał przed demodulacją; <math>t</math> - czas odpowiadający momentowi akwizycji próbki z danej głębokości; możemy przyjąć uproszczone założenie, że: | gdzie <math>IQ</math> - sygnał po demodulacji; <math>RF</math> - sygnał przed demodulacją; <math>t</math> - czas odpowiadający momentowi akwizycji próbki z danej głębokości; możemy przyjąć uproszczone założenie, że: | ||
<math>t=2y/c </math>; jak widać, pierwszy wymiar (szerokość) jest w naszej procedurze nieistotny. | <math>t=2y/c </math>; jak widać, pierwszy wymiar (szerokość) jest w naszej procedurze nieistotny. | ||
| − | Po demodulacji | + | Po demodulacji sygnał należy przefiltrować dolnoprzepustowo w zakresie pasma podstawowego (tzw. baseband). Dla naszych danych wystarczający powinien być filtr o częstotliwości odcięcia równej 5.55MHz. |
| − | + | ||
| + | ===Zadanie=== | ||
# Zbadać widmo amplitudowe sygnału przed i po demodulacji (po filtrowaniu). Jak zmieniło się widmo? Gdzie jest położona średnia widma? Czy rozkłady dla ujemnych i dodatnich częstotliwości są swoimi odbiciami? | # Zbadać widmo amplitudowe sygnału przed i po demodulacji (po filtrowaniu). Jak zmieniło się widmo? Gdzie jest położona średnia widma? Czy rozkłady dla ujemnych i dodatnich częstotliwości są swoimi odbiciami? | ||
# Porównać widmo amplitudowe sygnału zdemodulowanego przed i po filtracji. Jakich składowych w częstości się pozbyliśmy (nie licząc szumu)? | # Porównać widmo amplitudowe sygnału zdemodulowanego przed i po filtracji. Jakich składowych w częstości się pozbyliśmy (nie licząc szumu)? | ||
| Linia 30: | Linia 36: | ||
==Estymator autokorelacyjny== | ==Estymator autokorelacyjny== | ||
===Rys teoretyczny=== | ===Rys teoretyczny=== | ||
| − | Dotychczas traktowaliśmy | + | Dotychczas traktowaliśmy rekonstruowane obrazy jako sygnały dwuwymiarowe. Teraz, do zmierzenia średniej prędkości obiektów poruszających się w danym punkcie, konieczna będzie analiza wielu następujących po sobie obrazów, które zostały zebrane ze stałym interwałem czasowym (tzw. PRF - Pulse Repetition Frequency). W poniższych rozważaniach pomijamy wymiary przestrzenne - całe rozumowania przeprowadzone są dla sygnału <math>s(i)</math> na ustalonej głębokości i szerokości. Należy mieć na uwadze, że w praktyce ciężko mówić o estymacji prędkości w punkcie, ponieważ w naszej procedurze estymacji uwzględniamy efektywnie informacje z pewnego obszaru pomiarowego (energia danego piksela zawiera informację z pewnej objętości pomiarowej, co wynika z kształtu wiązki ultradźwiękowej). |
| − | Średnią prędkość będziemy mogli obliczyć korzystając ze średniego przesunięcia dopplerowskiego <math>\Delta f</math> w oparciu o szkolny wzór na [[Fizyka_III/Fale_dźwiękowe#Efekt_Dopplera|częstotliwość Dopplera]]: | + | Średnią prędkość będziemy mogli obliczyć korzystając ze średniego przesunięcia dopplerowskiego <math>\Delta f</math> w oparciu o szkolny wzór na [[Fizyka_III/Fale_dźwiękowe#Efekt_Dopplera|częstotliwość Dopplera]]: |
| − | <math>\Delta f=\frac{2f_{0}v\mbox{cos}\theta}{c}</math> | + | |
| − | gdzie <math>v</math> średnia prędkość w punkcie pomiarowym; <math>\theta</math> kąt między kierunkiem przepływu a wiązką nadawczą. | + | <math>\Delta f=\frac{2f_{0}v\mbox{cos}\theta}{c}</math>, |
| − | Przesunięcie dopplerowskie jest różnicą między średnią częstotliwością <math>f_0</math> sygnału nadanego a średnią częstotliwością <math>f_s</math> sygnału odebranego (pochodzącego od rozpraszaczy przemieszczających się w kierunku do lub od głowicy). Przypomnijmy, że zdemodulowany sygnał jest sygnałem o widmie pasmowym położonym w pobliżu częstości zerowej. Pozwala nam to przyjąć, że średnie przesunięcie częstotliwości odpowiada średniej częstotliwości tego sygnału | + | |
| − | + | gdzie <math>v</math> średnia prędkość w punkcie pomiarowym; <math>\theta</math> kąt między kierunkiem przepływu a wiązką nadawczą. | |
| − | Średnia częstość kołowa <math>\bar{\omega}</math> widma dopplerowskiego <math>P(\omega)</math> może być zdefiniowana jako | + | Przesunięcie dopplerowskie jest różnicą między średnią częstotliwością <math>f_0</math> sygnału nadanego a średnią częstotliwością <math>f_s</math> sygnału odebranego (pochodzącego od rozpraszaczy przemieszczających się w kierunku do lub od głowicy). Przypomnijmy, że zdemodulowany sygnał jest sygnałem o widmie pasmowym położonym w pobliżu częstości zerowej. Pozwala nam to przyjąć, że średnie przesunięcie częstotliwości odpowiada średniej częstotliwości tego sygnału <math>\Delta f = f_s-f_0 = f_s</math>. |
| + | Średnią częstotliwość możemy estymować na wiele sposób - np. licząc średnią ważoną z widma otrzymanego przez dyskretną transformację Fouriera. My zastosujemy do tego estymator autokorelacyjny<ref>Kasai, Chihiro, et al. "Real-time two-dimensional blood flow imaging using an autocorrelation technique." IEEE Trans. Sonics Ultrason 32.3 (1985): 458-464.</ref>, oparty na czasowej reprezentacji sygnału. | ||
| + | Średnia częstość kołowa <math>\bar{\omega}</math> widma dopplerowskiego <math>P(\omega)</math> może być zdefiniowana jako | ||
| + | |||
<math>\bar{\omega}=\frac{\int^{\infty}_{-\infty}\omega P(\omega)\mbox{d}\omega}{P(\omega)\mbox{d}\omega}</math> | <math>\bar{\omega}=\frac{\int^{\infty}_{-\infty}\omega P(\omega)\mbox{d}\omega}{P(\omega)\mbox{d}\omega}</math> | ||
| − | + | ||
| − | Jednocześnie, przy założeniu słabej stacjonarności sygnału dopplerowskiego, na mocy [[Twierdzenie_Wienera-Chinczyna|twierdzenia Wienera-Chinczyna]], funkcję autokorelacji <math>R(\tau)</math> tego sygnału możemy wyrazić jako | + | Jednocześnie, przy założeniu słabej stacjonarności sygnału dopplerowskiego, na mocy [[Twierdzenie_Wienera-Chinczyna|twierdzenia Wienera-Chinczyna]], funkcję autokorelacji <math>R(\tau)</math> tego sygnału możemy wyrazić jako: |
| − | <math>R(\tau)=\int^{\infty}_{-\infty} P(\omega)e^{j\omega\tau}\mbox{d}\omega</math> | + | |
| − | + | <math> R(\tau)=\int^{\infty}_{-\infty} P(\omega)e^{j\omega\tau}\mbox{d}\omega</math> | |
| − | Różniczkując powyższe dostajemy | + | |
| − | <math>\dot{R}(\tau)=j\int^{\infty}_{-\infty} \omega P(\omega)e^{j\omega\tau}\mbox{d}\omega</math> | + | Różniczkując powyższe dostajemy: |
| − | oraz | + | |
| − | <math>\ddot{R}(\tau)=-\int^{\infty}_{-\infty} \omega^{2} P(\omega)e^{j\omega\tau}\mbox{d}\omega</math> | + | <math> \dot{R}(\tau)=j\int^{\infty}_{-\infty} \omega P(\omega)e^{j\omega\tau}\mbox{d}\omega</math> |
| − | Stąd, częstotliwość średnia możemy być również przedstawiona jako | + | |
| − | <math>\bar{\omega}=-j\frac{\dot{R}(0)}{R(0)}</math> | + | oraz |
| + | |||
| + | <math> \ddot{R}(\tau)=-\int^{\infty}_{-\infty} \omega^{2} P(\omega)e^{j\omega\tau}\mbox{d}\omega</math>. | ||
| + | |||
| + | Stąd, częstotliwość średnia możemy być również przedstawiona jako | ||
| + | |||
| + | <math> \bar{\omega}=-j\frac{\dot{R}(0)}{R(0)}</math> | ||
| + | |||
W celu uproszczenia obliczeń przyjmuje się często następujące uproszczenie | W celu uproszczenia obliczeń przyjmuje się często następujące uproszczenie | ||
| − | + | ||
| − | gdzie <math>A(\tau)</math> jest funkcją parzystą i <math>e^{j\phi(\tau)}</math> jest funkcją nieparzystą. Wtedy | + | <math> R(\tau)= |R(\tau)|e^{j\phi(\tau)}=A(\tau)e^{j\phi(\tau)} </math>, |
| − | + | ||
| + | gdzie <math>A(\tau)</math> jest funkcją parzystą i <math>e^{j\phi(\tau)}</math> jest funkcją nieparzystą. Wtedy | ||
| + | |||
| + | <math> \dot{R}(\tau)=(\dot{A}(\tau)+jA(\tau)\dot{\phi}(\tau)e^{j\phi(\tau)} </math> | ||
| + | |||
i stąd | i stąd | ||
| − | + | ||
| + | <math> \dot{R}(0)=jA(0)\dot{\phi}(0) </math> | ||
| + | |||
oraz | oraz | ||
| − | + | ||
| + | <math> R(0)=A(0) </math>. | ||
| + | |||
Korzystając ze wcześniejszych równań dostajemy | Korzystając ze wcześniejszych równań dostajemy | ||
| − | + | ||
| − | gdzie <math>T_{PRF}</math> - czas między kolejnymi strzałami. | + | <math>\bar{\omega}=\dot{\phi}(0)\approx \frac{\phi(T_{PRF})-\phi(0)}{T_{PRF}}=\frac{\phi(T_{PRF})}{T_{PRF}}=\frac{1}{T_{PRF}}\frac{\mbox{Im}(R(T_{PRF}))}{\mbox{Re}(R(T_{PRF}))} </math>, |
| + | |||
| + | gdzie <math>T_{PRF}</math> - czas między kolejnymi strzałami (odwrotność PRF). | ||
| + | |||
====Estymator Millera-Rochwargera==== | ====Estymator Millera-Rochwargera==== | ||
Wartość <math>R(T_{PRF})</math> estymować możemy np. w oparciu o estymator Millera-Rochwargera <ref>Miller, Kenneth, and M. Rochwarger. "A covariance approach to spectral moment estimation." IEEE Transactions on Information Theory 18.5 (1972): 588-596.</ref>. Jest to [[wikipedia:Maximum_likelihood_estimation|estymator maksymalnej wiarygodności]] (maximum likehood estimator). Estymator ten jest skonstruowany dla par obserwacji zespolonego procesu <math>s</math> próbkowanych w równych odstępach czasu (w naszym przypadku <math>T_{PRF}</math>). W naszym przypadku jako pary obserwacji traktuje się pary próbek z kolejnych par następujących po sobie pomiarów (oddzielonych wartością <math>T_{PRF}</math>). Otrzymujemy wtedy oszacowanie wartości autokorelacji w oknie czasowym długości <math>N-1</math> | Wartość <math>R(T_{PRF})</math> estymować możemy np. w oparciu o estymator Millera-Rochwargera <ref>Miller, Kenneth, and M. Rochwarger. "A covariance approach to spectral moment estimation." IEEE Transactions on Information Theory 18.5 (1972): 588-596.</ref>. Jest to [[wikipedia:Maximum_likelihood_estimation|estymator maksymalnej wiarygodności]] (maximum likehood estimator). Estymator ten jest skonstruowany dla par obserwacji zespolonego procesu <math>s</math> próbkowanych w równych odstępach czasu (w naszym przypadku <math>T_{PRF}</math>). W naszym przypadku jako pary obserwacji traktuje się pary próbek z kolejnych par następujących po sobie pomiarów (oddzielonych wartością <math>T_{PRF}</math>). Otrzymujemy wtedy oszacowanie wartości autokorelacji w oknie czasowym długości <math>N-1</math> | ||
| − | + | ||
| + | <math>\bar{\omega}=\frac{1}{T_{PRF}}\mbox{arctan}\frac{Im(\sum^{N-2}_{i=0}s(i+1)\cdot \overline{s(i)})}{Re(\sum^{N-2}_{i=0}s(i+1)\cdot \overline{s(i)})} </math> | ||
| + | |||
Pamiętając zależność między średnią częstotliwością <math>f_s</math> a średnią częstością kołową <math>fs=(1/2\pi)\bar{\omega}</math> dostajemy | Pamiętając zależność między średnią częstotliwością <math>f_s</math> a średnią częstością kołową <math>fs=(1/2\pi)\bar{\omega}</math> dostajemy | ||
| − | + | ||
| − | <math>f_s=\frac{1}{2\pi T_{PRF}}\mbox{arctan}\frac{Im(\sum^{N-2}_{i=0}s(i+1)\cdot \overline{s(i)})}{Re(\sum^{N-2}_{i=0}s(i+1)\cdot \overline{s(i)})} </math | + | <math>f_s=\frac{1}{2\pi T_{PRF}}\mbox{arctan}\frac{Im(\sum^{N-2}_{i=0}s(i+1)\cdot \overline{s(i)})}{Re(\sum^{N-2}_{i=0}s(i+1)\cdot \overline{s(i)})} </math> |
===Zadanie=== | ===Zadanie=== | ||
| − | Proszę przygotować funkcję estymującą częstotliwość średnią w oparciu o powyższy estymator dla jednowymiarowego zespolonego | + | Proszę przygotować funkcję estymującą częstotliwość średnią w oparciu o powyższy estymator dla jednowymiarowego sygnału zespolonego. |
==Prezentacja Kolor== | ==Prezentacja Kolor== | ||
Po estymacji średnich prędkości w obszarach odpowiadających punktom na siatce użytej do rekonstrukcji obrazu, możemy nałożyć taką mapę na obraz B-mode w celu uzyskania obrazu "Kolor". Mając tablicę z danymi B-mode oraz tablicę prędkości, możemy otrzymać połączony obraz za pomocą poniższego skryptu: | Po estymacji średnich prędkości w obszarach odpowiadających punktom na siatce użytej do rekonstrukcji obrazu, możemy nałożyć taką mapę na obraz B-mode w celu uzyskania obrazu "Kolor". Mając tablicę z danymi B-mode oraz tablicę prędkości, możemy otrzymać połączony obraz za pomocą poniższego skryptu: | ||
| − | <source lang=python> | + | |
| − | #BMode - tablica zrekonstruowanych danych po przefiltrowaniu, obwiedni itp. | + | <source lang=python> |
| − | #flow - tablica przepływów | + | # BMode - tablica zrekonstruowanych danych po przefiltrowaniu, obwiedni itp. |
| + | # flow - tablica przepływów | ||
Frame = Image.fromarray(np.uint8(cm.bone(BMode)*255)) | Frame = Image.fromarray(np.uint8(cm.bone(BMode)*255)) | ||
flowMask = np.copy(flow) | flowMask = np.copy(flow) | ||
| Linia 88: | Linia 118: | ||
Frame.paste(flow, (0,0), flow) | Frame.paste(flow, (0,0), flow) | ||
</source> | </source> | ||
| + | |||
===Zadanie=== | ===Zadanie=== | ||
Zaimplementować funkcję otrzymującą na wejściu trójwymiarową tablicę zawierającą obrazy RF z <math>N</math> kolejnych chwil pomiarowych i zwracającą obrazy z nałożoną na nią mapą prędkości obliczonych przy użyciu estymatora autokorelacyjnego. | Zaimplementować funkcję otrzymującą na wejściu trójwymiarową tablicę zawierającą obrazy RF z <math>N</math> kolejnych chwil pomiarowych i zwracającą obrazy z nałożoną na nią mapą prędkości obliczonych przy użyciu estymatora autokorelacyjnego. | ||
| Linia 95: | Linia 126: | ||
===Rozpoznawanie ruchu=== | ===Rozpoznawanie ruchu=== | ||
| − | Jedną z pierwszy obserwacji jakiej można dokonać, to zauważenie, że nasza mapa jest niezerowa w punktach w których nie spodziewamy się żadnego ruchu. Pewnym rozwiązaniem tego problemu może być zastosowanie prostego kryterium rozpoznawania ruchu. Możemy przyjąć, że sygnał pochodzący od struktur pozostających w spoczynku powinien być stały w czasie. W praktyce sygnały takie różnić będą się głównie o składową szumu elektronicznego. Jednocześnie, sygnał pochodzący od ruchomych struktur będzie charakteryzować się względnie dużą zmiennością w czasie. | + | Jedną z pierwszy obserwacji jakiej można dokonać, to zauważenie, że nasza mapa jest niezerowa w punktach w których nie spodziewamy się żadnego ruchu. Pewnym rozwiązaniem tego problemu może być zastosowanie prostego kryterium rozpoznawania ruchu. Możemy przyjąć, że sygnał pochodzący od struktur pozostających w spoczynku powinien być stały w czasie. W praktyce sygnały takie różnić będą się głównie o składową szumu elektronicznego. Jednocześnie, sygnał pochodzący od ruchomych struktur będzie charakteryzować się względnie dużą zmiennością w czasie. |
| + | |||
====Zadanie==== | ====Zadanie==== | ||
Zaimplementować procedurę zerującą estymatę prędkości w punkcie, jeśli średnia różnica między wartościami sygnału w tym punkcie w kolejnych chwilach czasu jest względnie mała (próg proszę dobrać eksperymentalnie - zaczynając np. od progu 10% średniej różnicy w obrazie). | Zaimplementować procedurę zerującą estymatę prędkości w punkcie, jeśli średnia różnica między wartościami sygnału w tym punkcie w kolejnych chwilach czasu jest względnie mała (próg proszę dobrać eksperymentalnie - zaczynając np. od progu 10% średniej różnicy w obrazie). | ||
===Filtr medianowy=== | ===Filtr medianowy=== | ||
| − | Dobrym rozwiązaniem w tego typu przypadkach jest zastosowanie filtru medianowego. Filtr medianowy przekształca wartość w punkcie na medianę wartości sygnału w ustalonej liczbie sąsiednich próbek (w obu wymiarach): | + | Dobrym rozwiązaniem w tego typu przypadkach jest zastosowanie filtru medianowego. Filtr medianowy przekształca wartość w punkcie na medianę wartości sygnału w ustalonej liczbie sąsiednich próbek (w obu wymiarach): |
| − | <math>s_{med}(x,y) = \sum^{K-1}_{i=0}\sum^{K-1}_{j=0}s(x+i,y+j) </math> | + | |
| + | <math>s_{med}(x,y) = \sum^{K-1}_{i=0}\sum^{K-1}_{j=0}s(x+i,y+j) </math>, | ||
| + | |||
gdzie <math>K</math> - rozmiar okna filtru. | gdzie <math>K</math> - rozmiar okna filtru. | ||
Filtr taki usuwa skrajne wartości w dużo większym stopniu niż np. filtr oparty o średnią arytmetyczną. W bibliotece scipy istnieje gotowa funkcja filtrująca tablicę filtrem medianowym: | Filtr taki usuwa skrajne wartości w dużo większym stopniu niż np. filtr oparty o średnią arytmetyczną. W bibliotece scipy istnieje gotowa funkcja filtrująca tablicę filtrem medianowym: | ||
| + | |||
<source lang=python> | <source lang=python> | ||
scipy.signal.medfilt2d(array, K) | scipy.signal.medfilt2d(array, K) | ||
</source> | </source> | ||
| + | |||
====Zadanie==== | ====Zadanie==== | ||
| − | Porównać mapy prędkości przed i po filtracji medianowej (dla kilku różnych rozmiarów okna filtracji) | + | Porównać mapy prędkości przed i po filtracji medianowej (dla kilku różnych rozmiarów okna filtracji). |
| + | |||
| + | ---- | ||
Aktualna wersja na dzień 08:30, 29 lip 2016
Spis treści
Metoda dopplerowska impulsowa (Pulsed Wave)
Do dyspozycji mamy zestaw zrekonstruowanych danych RF (link) z 64 kolejnych nadań pod stałym kątem (zerowym) falą płaską o parametrach:
f0 = 5.5e6 # Częstotliwość nadawcza [Hz]
z_step = 3.079291762894534e-05 # Odległość między kolejnymi punktami w głębokości na siatce rekonstruowanego obrazu [m]
PRF = 1000 # Pulse Repetition Frequency [Hz]
T_PRF = 1./PRF # czas między kolejnymi nadaniami [s]
Obrazowany jest przekrój fantomu przepływowego złożonego z rurek umieszczonych w materiale tkankopodobnym.
Pompa wymusza jednostajny przepływ płynu krwiopodobnego znajdującego się w rurkach. Będziemy starali się wykorzystać metodę dopplerowską do stworzenia mapy obrazującej zwrot i prędkość przepływu. Średnie odchylenie dopplerowskie szacować będziemy przy użyciu estymatora autokorelacyjnego.
Demodulacja sygnału RF
Estymator autokorelacyjny stosowany jest na zdemodulowanym sygnale kwadraturowym I/Q (ang. In-Phase/Quadrature). Sygnał RF rejestrowany bezpośrednio z przetworników odbiorczych jest sygnałem rzeczywistym (zerowa część urojona) o pasmowej charakterystyce widmowej. Informacja istotna z naszego punktu widzenia położona jest w paśmie, którego środek znajduje się częstotliwości nadawczej; szerokość tego pasma zależna jest od fizycznych właściwości głowicy ultradźwiękowej i nazywana jest pasmem przenoszenia głowicy. Demodulacja jest operacją pozwalającą na przekształcenie takiego sygnału w sygnał zespolony o paśmie położonym wokół częstotliwości zerowej. Taki zabieg pozwala na zmniejszenie częstotliwości próbkowania - potencjalnie poniżej częstotliwości Nyquista określonej dla składowych sygnału niezdemodulowanego.
Demodulację możemy przeprowadzić zarówno na danych surowych RF, jak i na danych po rekonstrukcji. W naszym wypadku zastosujemy to drugie rozwiązanie.
Na początku stworzymy funkcję dokonującą demodulacji każdego z obrazów, tj. dla każdej próbki o współrzędnych [math](x,y)[/math]
[math]IQ(x,y)=RF(x,y)\cdot e^{-i\cdot2\pi f_{0}t} [/math]
gdzie [math]IQ[/math] - sygnał po demodulacji; [math]RF[/math] - sygnał przed demodulacją; [math]t[/math] - czas odpowiadający momentowi akwizycji próbki z danej głębokości; możemy przyjąć uproszczone założenie, że: [math]t=2y/c [/math]; jak widać, pierwszy wymiar (szerokość) jest w naszej procedurze nieistotny. Po demodulacji sygnał należy przefiltrować dolnoprzepustowo w zakresie pasma podstawowego (tzw. baseband). Dla naszych danych wystarczający powinien być filtr o częstotliwości odcięcia równej 5.55MHz.
Zadanie
- Zbadać widmo amplitudowe sygnału przed i po demodulacji (po filtrowaniu). Jak zmieniło się widmo? Gdzie jest położona średnia widma? Czy rozkłady dla ujemnych i dodatnich częstotliwości są swoimi odbiciami?
- Porównać widmo amplitudowe sygnału zdemodulowanego przed i po filtracji. Jakich składowych w częstości się pozbyliśmy (nie licząc szumu)?
- Zmienić w demodulacji wartość częstotliwości nośnej (np. zmniejszyć o połowę) i ponownie porównać widmo przed i po demodulacji.
Estymator autokorelacyjny
Rys teoretyczny
Dotychczas traktowaliśmy rekonstruowane obrazy jako sygnały dwuwymiarowe. Teraz, do zmierzenia średniej prędkości obiektów poruszających się w danym punkcie, konieczna będzie analiza wielu następujących po sobie obrazów, które zostały zebrane ze stałym interwałem czasowym (tzw. PRF - Pulse Repetition Frequency). W poniższych rozważaniach pomijamy wymiary przestrzenne - całe rozumowania przeprowadzone są dla sygnału [math]s(i)[/math] na ustalonej głębokości i szerokości. Należy mieć na uwadze, że w praktyce ciężko mówić o estymacji prędkości w punkcie, ponieważ w naszej procedurze estymacji uwzględniamy efektywnie informacje z pewnego obszaru pomiarowego (energia danego piksela zawiera informację z pewnej objętości pomiarowej, co wynika z kształtu wiązki ultradźwiękowej). Średnią prędkość będziemy mogli obliczyć korzystając ze średniego przesunięcia dopplerowskiego [math]\Delta f[/math] w oparciu o szkolny wzór na częstotliwość Dopplera:
[math]\Delta f=\frac{2f_{0}v\mbox{cos}\theta}{c}[/math],
gdzie [math]v[/math] średnia prędkość w punkcie pomiarowym; [math]\theta[/math] kąt między kierunkiem przepływu a wiązką nadawczą. Przesunięcie dopplerowskie jest różnicą między średnią częstotliwością [math]f_0[/math] sygnału nadanego a średnią częstotliwością [math]f_s[/math] sygnału odebranego (pochodzącego od rozpraszaczy przemieszczających się w kierunku do lub od głowicy). Przypomnijmy, że zdemodulowany sygnał jest sygnałem o widmie pasmowym położonym w pobliżu częstości zerowej. Pozwala nam to przyjąć, że średnie przesunięcie częstotliwości odpowiada średniej częstotliwości tego sygnału [math]\Delta f = f_s-f_0 = f_s[/math]. Średnią częstotliwość możemy estymować na wiele sposób - np. licząc średnią ważoną z widma otrzymanego przez dyskretną transformację Fouriera. My zastosujemy do tego estymator autokorelacyjny[1], oparty na czasowej reprezentacji sygnału. Średnia częstość kołowa [math]\bar{\omega}[/math] widma dopplerowskiego [math]P(\omega)[/math] może być zdefiniowana jako
[math]\bar{\omega}=\frac{\int^{\infty}_{-\infty}\omega P(\omega)\mbox{d}\omega}{P(\omega)\mbox{d}\omega}[/math]
Jednocześnie, przy założeniu słabej stacjonarności sygnału dopplerowskiego, na mocy twierdzenia Wienera-Chinczyna, funkcję autokorelacji [math]R(\tau)[/math] tego sygnału możemy wyrazić jako:
[math] R(\tau)=\int^{\infty}_{-\infty} P(\omega)e^{j\omega\tau}\mbox{d}\omega[/math]
Różniczkując powyższe dostajemy:
[math] \dot{R}(\tau)=j\int^{\infty}_{-\infty} \omega P(\omega)e^{j\omega\tau}\mbox{d}\omega[/math]
oraz
[math] \ddot{R}(\tau)=-\int^{\infty}_{-\infty} \omega^{2} P(\omega)e^{j\omega\tau}\mbox{d}\omega[/math].
Stąd, częstotliwość średnia możemy być również przedstawiona jako
[math] \bar{\omega}=-j\frac{\dot{R}(0)}{R(0)}[/math]
W celu uproszczenia obliczeń przyjmuje się często następujące uproszczenie
[math] R(\tau)= |R(\tau)|e^{j\phi(\tau)}=A(\tau)e^{j\phi(\tau)} [/math],
gdzie [math]A(\tau)[/math] jest funkcją parzystą i [math]e^{j\phi(\tau)}[/math] jest funkcją nieparzystą. Wtedy
[math] \dot{R}(\tau)=(\dot{A}(\tau)+jA(\tau)\dot{\phi}(\tau)e^{j\phi(\tau)} [/math]
i stąd
[math] \dot{R}(0)=jA(0)\dot{\phi}(0) [/math]
oraz
[math] R(0)=A(0) [/math].
Korzystając ze wcześniejszych równań dostajemy
[math]\bar{\omega}=\dot{\phi}(0)\approx \frac{\phi(T_{PRF})-\phi(0)}{T_{PRF}}=\frac{\phi(T_{PRF})}{T_{PRF}}=\frac{1}{T_{PRF}}\frac{\mbox{Im}(R(T_{PRF}))}{\mbox{Re}(R(T_{PRF}))} [/math],
gdzie [math]T_{PRF}[/math] - czas między kolejnymi strzałami (odwrotność PRF).
Estymator Millera-Rochwargera
Wartość [math]R(T_{PRF})[/math] estymować możemy np. w oparciu o estymator Millera-Rochwargera [2]. Jest to estymator maksymalnej wiarygodności (maximum likehood estimator). Estymator ten jest skonstruowany dla par obserwacji zespolonego procesu [math]s[/math] próbkowanych w równych odstępach czasu (w naszym przypadku [math]T_{PRF}[/math]). W naszym przypadku jako pary obserwacji traktuje się pary próbek z kolejnych par następujących po sobie pomiarów (oddzielonych wartością [math]T_{PRF}[/math]). Otrzymujemy wtedy oszacowanie wartości autokorelacji w oknie czasowym długości [math]N-1[/math]
[math]\bar{\omega}=\frac{1}{T_{PRF}}\mbox{arctan}\frac{Im(\sum^{N-2}_{i=0}s(i+1)\cdot \overline{s(i)})}{Re(\sum^{N-2}_{i=0}s(i+1)\cdot \overline{s(i)})} [/math]
Pamiętając zależność między średnią częstotliwością [math]f_s[/math] a średnią częstością kołową [math]fs=(1/2\pi)\bar{\omega}[/math] dostajemy
[math]f_s=\frac{1}{2\pi T_{PRF}}\mbox{arctan}\frac{Im(\sum^{N-2}_{i=0}s(i+1)\cdot \overline{s(i)})}{Re(\sum^{N-2}_{i=0}s(i+1)\cdot \overline{s(i)})} [/math]
Zadanie
Proszę przygotować funkcję estymującą częstotliwość średnią w oparciu o powyższy estymator dla jednowymiarowego sygnału zespolonego.
Prezentacja Kolor
Po estymacji średnich prędkości w obszarach odpowiadających punktom na siatce użytej do rekonstrukcji obrazu, możemy nałożyć taką mapę na obraz B-mode w celu uzyskania obrazu "Kolor". Mając tablicę z danymi B-mode oraz tablicę prędkości, możemy otrzymać połączony obraz za pomocą poniższego skryptu:
# BMode - tablica zrekonstruowanych danych po przefiltrowaniu, obwiedni itp.
# flow - tablica przepływów
Frame = Image.fromarray(np.uint8(cm.bone(BMode)*255))
flowMask = np.copy(flow)
flowMask = np.abs(flowMask)
flowMask = flowMask/(np.max(flowMask))*255
flow = flow+np.abs(np.min(flow))
flow = flow/np.max(flow)
flow = Image.fromarray(np.uint8(cm.jet(flow)*255))
flowMask = Image.fromarray(np.uint8(flowMask), 'L')
flow.putalpha(flowMask)
Frame.paste(flow, (0,0), flow)
Zadanie
Zaimplementować funkcję otrzymującą na wejściu trójwymiarową tablicę zawierającą obrazy RF z [math]N[/math] kolejnych chwil pomiarowych i zwracającą obrazy z nałożoną na nią mapą prędkości obliczonych przy użyciu estymatora autokorelacyjnego.
Filtracja obrazu
Mapa częstości estymowana metodą autokorelacyjną jest dość wrażliwa na błędy estymacji powodowane m.in. obecność w sygnale informacji z dużego obszaru pomiarowego. Stosować można kilka metod mających na celu poprawę wynikowego obrazu - progowanie (zignorowanie względnie małych prędkości), rozpoznawanie ruchu i filtrowanie.
Rozpoznawanie ruchu
Jedną z pierwszy obserwacji jakiej można dokonać, to zauważenie, że nasza mapa jest niezerowa w punktach w których nie spodziewamy się żadnego ruchu. Pewnym rozwiązaniem tego problemu może być zastosowanie prostego kryterium rozpoznawania ruchu. Możemy przyjąć, że sygnał pochodzący od struktur pozostających w spoczynku powinien być stały w czasie. W praktyce sygnały takie różnić będą się głównie o składową szumu elektronicznego. Jednocześnie, sygnał pochodzący od ruchomych struktur będzie charakteryzować się względnie dużą zmiennością w czasie.
Zadanie
Zaimplementować procedurę zerującą estymatę prędkości w punkcie, jeśli średnia różnica między wartościami sygnału w tym punkcie w kolejnych chwilach czasu jest względnie mała (próg proszę dobrać eksperymentalnie - zaczynając np. od progu 10% średniej różnicy w obrazie).
Filtr medianowy
Dobrym rozwiązaniem w tego typu przypadkach jest zastosowanie filtru medianowego. Filtr medianowy przekształca wartość w punkcie na medianę wartości sygnału w ustalonej liczbie sąsiednich próbek (w obu wymiarach):
[math]s_{med}(x,y) = \sum^{K-1}_{i=0}\sum^{K-1}_{j=0}s(x+i,y+j) [/math],
gdzie [math]K[/math] - rozmiar okna filtru. Filtr taki usuwa skrajne wartości w dużo większym stopniu niż np. filtr oparty o średnią arytmetyczną. W bibliotece scipy istnieje gotowa funkcja filtrująca tablicę filtrem medianowym:
scipy.signal.medfilt2d(array, K)
Zadanie
Porównać mapy prędkości przed i po filtracji medianowej (dla kilku różnych rozmiarów okna filtracji).
- ↑ Kasai, Chihiro, et al. "Real-time two-dimensional blood flow imaging using an autocorrelation technique." IEEE Trans. Sonics Ultrason 32.3 (1985): 458-464.
- ↑ Miller, Kenneth, and M. Rochwarger. "A covariance approach to spectral moment estimation." IEEE Transactions on Information Theory 18.5 (1972): 588-596.