TI/Programowanie dla Fizyków Medycznych/Optymalizacja: Różnice pomiędzy wersjami
| (Nie pokazano 13 wersji utworzonych przez jednego użytkownika) | |||
| Linia 20: | Linia 20: | ||
[[Plik:opt1.png]] | [[Plik:opt1.png]] | ||
| − | Na rozważanym przedziale [0.2,2] powyższa | + | Na rozważanym przedziale [0.2,2] powyższa funkcja ma tylko jedno ekstremum lokalne. Taką funkcję nazywamy unimodalną. Zmienna licznikTestowej umożliwi nam zliczanie wywołań funkcji testowej przez analizowane procedury. |
| − | Zagadnienie którym teraz będziemy się zajmować to problem numerycznego znajdowania takiego ekstremum. Jak | + | Zagadnienie, którym teraz będziemy się zajmować to problem numerycznego znajdowania takiego ekstremum. Jak w każdym problemie numerycznym ekstremum szukać będziemy zakładając pewną dokładność otrzymanego wyniku, którą oznaczmy xtol. Na wstępie przyjmijmy, że poszukujemy ekstremum z dokładnością xtol=0.01. Najprostszą metodą będzie policzenie wartości funkcji dla wszystkich wartości x z podanego przedziału co xtol. Jest to metoda siłowa i wielokrotnie licząca wartość funkcji. Jej kod możemy znaleźć poniżej. |
<source lang="python"> | <source lang="python"> | ||
def bruteForce(func,xmin,xmax,args=(),xtol=0.01): | def bruteForce(func,xmin,xmax,args=(),xtol=0.01): | ||
| Linia 28: | Linia 28: | ||
return xlist[ylist.index(max(ylist))] | return xlist[ylist.index(max(ylist))] | ||
</source> | </source> | ||
| − | Innym, znacznie efektywniejszym sposobem znajdowania minimum | + | Innym, znacznie efektywniejszym sposobem znajdowania minimum może być następująca procedura rekurencyjna: |
| − | *podzielmy | + | *podzielmy przedział [xmin,xmax] na 3 równe część: [xmin,xL],[xL,xR] oraz [xR,xmax] |
| − | *jeżeli wartość funkcji w xL jest mniejsza od wartości funkcji w xR to powtórz procedurę dla przedziału [xmin,xR]. W przeciwnym przypadku powtórz | + | *jeżeli wartość funkcji w xL jest mniejsza od wartości funkcji w xR to powtórz procedurę dla przedziału [xmin,xR]. W przeciwnym przypadku powtórz procedurę dla przedziału [xL,xmax]. |
| − | *zakończ działanie gdy badany przedział jest krótszy | + | *zakończ działanie gdy badany przedział jest krótszy niż xtol. |
| − | Przykładowa | + | Przykładowa implementacja tej metody wygląda następująco |
<source lang="python"> | <source lang="python"> | ||
def twoMidPointsR(func,xmin,xmax,args=(),xtol=0.01): | def twoMidPointsR(func,xmin,xmax,args=(),xtol=0.01): | ||
| Linia 45: | Linia 45: | ||
return twoMidPointsR(func,xL,xmax,args,xtol) | return twoMidPointsR(func,xL,xmax,args,xtol) | ||
</source> | </source> | ||
| − | Tą metodą możemy już szukać minimum | + | Tą metodą możemy już szukać minimum z dowolną dokładnością, co nie będzie skutkowało znacznie większym czasem obliczeń. Zauważmy jednak, że w każdej iteracji wartość minimalizowanej funkcji liczona jest dwukrotnie. Jeżeli mamy do czynienia z funkcją, dla której obliczenie pojedynczej wartości jest bardzo czasochłonne to warto się zastanowić czy nie można tego wyniku poprawić. Zauważmy, że dla działania tej metody wcale nie jest konieczne dzielenie badanego odcinka dokładnie na trzy równe części. Można dokonać tego podziału w zupełnie innej proporcji. Warto tak dobrać punkty xL i xR, aby xR pokrywał się z xL (lub xL z xR) w kolejnym kroku iteracji. Jeżeli dodatkowo stworzymy zmienne przechowujące wcześniej liczone wartości funkcji to uda nam się ograniczyć liczbę wywołań funkcji o połowę. Opisana metoda to tak zwana '''metoda złotego podziału'''. Przykładowa implementacja wygląda następująco |
<source lang="python"> | <source lang="python"> | ||
| Linia 71: | Linia 71: | ||
return 0.5*(xmax+xmin) | return 0.5*(xmax+xmin) | ||
| + | </source> | ||
| + | Napisanej metody optymalizacji możemy użyć w celu dopasowania funkcji do danych empirycznych metodą najmniejszych kwadratów. Przykład takiego zastosowania poniżej. | ||
| − | + | <source lang="python"> | |
| − | + | #suma kwadratów | |
| − | |||
| − | |||
| − | # | ||
def squares(a,func,xlist,ylist): | def squares(a,func,xlist,ylist): | ||
return sum([(func(xlist[i],*a)-ylist[i])**2 for i in range(len(xlist))]) | return sum([(func(xlist[i],*a)-ylist[i])**2 for i in range(len(xlist))]) | ||
| Linia 82: | Linia 81: | ||
#funkcja liniowa | #funkcja liniowa | ||
def liniowa(x,a): return x*a | def liniowa(x,a): return x*a | ||
| − | |||
| − | |||
| − | |||
#generujemy przykladowe xlist | #generujemy przykladowe xlist | ||
xlist=np.arange(0,1,0.001) | xlist=np.arange(0,1,0.001) | ||
| + | |||
#generujemy wartosci funkcji z szumem | #generujemy wartosci funkcji z szumem | ||
| − | ylist=[ | + | ylist=[liniowa(x,1.23)+0.000001*np.random.randn() for x in xlist] |
| − | # | + | |
| − | + | #najlepsze dopasowanie metoda golden ration | |
| + | print GoldenRatioRearch(squares,0,10,args=(liniowa,xlist,ylist),xtol=0.01) | ||
| + | </source> | ||
| + | |||
| + | ==Optymalizacja wielowymiarowa== | ||
| + | Przejście od optymalizacji jedno- do wielowymiarowej fundamentalnie komplikuje problem. Pierwszym problemem jest istnienie tak zwanych punktów siodłowych. Nie istnieją zatem metody które zawsze znajdują szukane minimum, nawet jeżeli wiadomo że takie istnieje. Najpopularniejszą metodą jest downhill symplex lub inaczej metoda Neldera-Meada. Z powodu znacznego stopnia komplikacji nie będziemy jej samodzielnie implementować, a jedynie posłużymy się implementacją z biblioteki scipy.optimize. Dzięki niej możemy np. dopasowywać funkcję z więcej niż jednym parametrem do danych eksperymentalnych. | ||
| + | <source lang="python"> | ||
| + | import scipy.optimize as so | ||
| + | |||
| + | #suma kwadratów | ||
| + | def squares(a,func,xlist,ylist): | ||
| + | return sum([(func(xlist[i],*a)-ylist[i])**2 for i in range(len(xlist))]) | ||
| − | # | + | #funkcja liniowa |
| − | + | def liniowa(x,a,b): return x*a+b | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | # | + | #generujemy przykladowe xlist |
| − | + | xlist=np.arange(0,1,0.001) | |
| − | |||
| − | #najlepsze dopasowanie metoda | + | #generujemy wartosci funkcji z szumem |
| − | print so.fmin(squares,(1,0),args=( | + | ylist=[liniowa(x,1.23,-0.73)+0.000001*np.random.randn() for x in xlist] |
| + | |||
| + | #najlepsze dopasowanie metoda golden ration | ||
| + | print so.fmin(squares,(1,0),args=(liniowa,xlist,ylist)) | ||
</source> | </source> | ||
| + | Oczywiście dopasowywanie możemy przeprowadzać nie tylko metodą najmniejszych kwadratów. | ||
| + | ===Zadanie - rozkład Cauchy'ego=== | ||
| + | Wylosuj 10000 liczb z rozkładu Cauchy'ego z parametrami loc=1.23 i scale=2.0. Do wylosowanych danych dopasuj rozkład Cauche'ego trzema metodami | ||
| + | *METODA 1 - stwórz histogram otrzymanych wartości, znormalizuj go i metodą najmniejszych kwadratów dopasauj gęstość rozkładu do histogramu | ||
| + | *METODA 2 - dopasuj gęstość rozkładu do wylosowanych danych metodą największej wiarygodności | ||
| + | *METODA 3 - z wylosowanych danych stwórz dystrybuantę empiryczną. Metodą najmniejszych kwadratów dopasuj dystrybuantę rozkładu Cauchy'ego do dystrybuanty empirycznej. | ||
| + | |||
| + | ===Rozwiązanie=== | ||
| − | |||
<source lang="python"> | <source lang="python"> | ||
| − | |||
| − | |||
import scipy.optimize as so | import scipy.optimize as so | ||
| − | |||
| − | |||
| − | |||
def rho_cauchy(x,loc,scale): | def rho_cauchy(x,loc,scale): | ||
return (np.pi*scale*(1.0+(x-loc)**2/(scale**2)))**(-1.0) | return (np.pi*scale*(1.0+(x-loc)**2/(scale**2)))**(-1.0) | ||
| Linia 129: | Linia 134: | ||
| − | #losujemy 10000 liczb z rozkladu | + | #losujemy 10000 liczb z rozkladu Cauchyego o loc=1.23 i scale=2.0 |
x=2*np.random.standard_cauchy(10000)+1.23 | x=2*np.random.standard_cauchy(10000)+1.23 | ||
N=len(x) | N=len(x) | ||
| Linia 186: | Linia 191: | ||
</source> | </source> | ||
| − | ===Zadanie=== | + | ===Zadanie - Data Container=== |
| − | Napisz | + | Napisz klasę funkcja przyjmującą w konstruktorze parametry funkcji i posiadającą reprezentację tekstową. Napisz dowolną funkcję dziedziczącą po klasie funkcja, której metoda call przyjmuje jeden argument i zwraca wartość funkcji dla podanego argumentu i parametrów podanych w konstruktorze. |
| + | Napisz klasę DataContainer przyjmującą w konstruktorze dwie serie danych empirycznych o tej samej długości odpowiadające współrzędnym x i y. Obiekt klasy DataContainer powinien być wyposażony w metodę o nazwie fit, która przyjmuje jako argument obiekt klasy funkcja. Metoda fit powinna zwracać obiekt takiej samej klasy jak otrzymany w argumencie, ale z parametrami, dla których funkcja jest najlepiej (metodą najmniejszych kwadratów) dopasowana do przechowywanych w obiekcie danych. | ||
| + | |||
| + | ===Rozwiązanie=== | ||
<source lang="python"> | <source lang="python"> | ||
import numpy as np | import numpy as np | ||
| Linia 236: | Linia 244: | ||
py.plot(d.x,map(f,d.x)) | py.plot(d.x,map(f,d.x)) | ||
py.show() | py.show() | ||
| − | |||
| − | |||
</source> | </source> | ||
[["Programowanie dla Fizyków Medycznych"]] | [["Programowanie dla Fizyków Medycznych"]] | ||
Aktualna wersja na dzień 13:18, 16 lut 2017
Spis treści
Optymalizacja jednowymiarowa
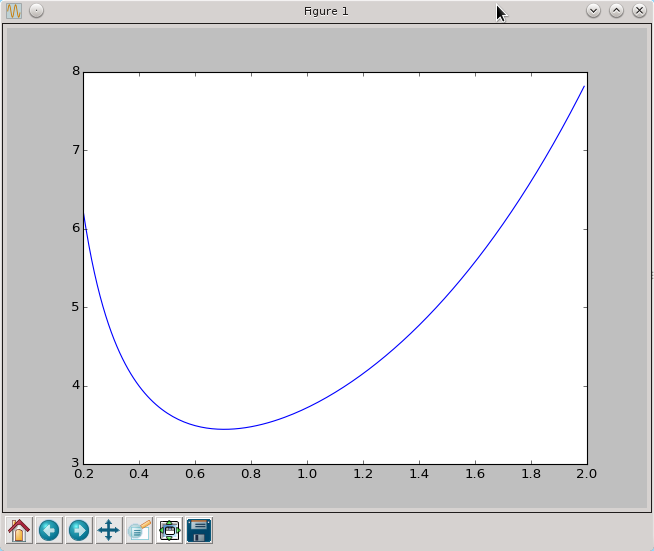
Omawianie zagadnienia optymalizacji rozpocznijmy od prostego przykładu. Zdefiniujmy pewną funkcję i zobaczmy jak wygląda jej wykres.
import numpy as np
import pylab as py
licznikTestowej=0
def testowa(x):
global licznikTestowej
licznikTestowej+=1
return 1/x+np.exp(x)
xtest=np.arange(0.2,2,0.01)
ytest=[testowa(x) for x in xtest]
py.plot(xtest,ytest)
py.show()
Na rozważanym przedziale [0.2,2] powyższa funkcja ma tylko jedno ekstremum lokalne. Taką funkcję nazywamy unimodalną. Zmienna licznikTestowej umożliwi nam zliczanie wywołań funkcji testowej przez analizowane procedury. Zagadnienie, którym teraz będziemy się zajmować to problem numerycznego znajdowania takiego ekstremum. Jak w każdym problemie numerycznym ekstremum szukać będziemy zakładając pewną dokładność otrzymanego wyniku, którą oznaczmy xtol. Na wstępie przyjmijmy, że poszukujemy ekstremum z dokładnością xtol=0.01. Najprostszą metodą będzie policzenie wartości funkcji dla wszystkich wartości x z podanego przedziału co xtol. Jest to metoda siłowa i wielokrotnie licząca wartość funkcji. Jej kod możemy znaleźć poniżej.
def bruteForce(func,xmin,xmax,args=(),xtol=0.01):
xlist=np.arange(xmin,xmax,xtol)
ylist=[func(x,*args) for x in xlist]
return xlist[ylist.index(max(ylist))]
Innym, znacznie efektywniejszym sposobem znajdowania minimum może być następująca procedura rekurencyjna:
- podzielmy przedział [xmin,xmax] na 3 równe część: [xmin,xL],[xL,xR] oraz [xR,xmax]
- jeżeli wartość funkcji w xL jest mniejsza od wartości funkcji w xR to powtórz procedurę dla przedziału [xmin,xR]. W przeciwnym przypadku powtórz procedurę dla przedziału [xL,xmax].
- zakończ działanie gdy badany przedział jest krótszy niż xtol.
Przykładowa implementacja tej metody wygląda następująco
def twoMidPointsR(func,xmin,xmax,args=(),xtol=0.01):
if xmax-xmin<xtol: return 0.5*(xmax+xmin)
xL=xmin+(xmax-xmin)/3.0
xR=xmax-(xmax-xmin)/3.0
fxL=func(xL,*args)
fxR=func(xR,*args)
if fxL>fxR:
return twoMidPointsR(func,xmin,xR,args,xtol)
else:
return twoMidPointsR(func,xL,xmax,args,xtol)
Tą metodą możemy już szukać minimum z dowolną dokładnością, co nie będzie skutkowało znacznie większym czasem obliczeń. Zauważmy jednak, że w każdej iteracji wartość minimalizowanej funkcji liczona jest dwukrotnie. Jeżeli mamy do czynienia z funkcją, dla której obliczenie pojedynczej wartości jest bardzo czasochłonne to warto się zastanowić czy nie można tego wyniku poprawić. Zauważmy, że dla działania tej metody wcale nie jest konieczne dzielenie badanego odcinka dokładnie na trzy równe części. Można dokonać tego podziału w zupełnie innej proporcji. Warto tak dobrać punkty xL i xR, aby xR pokrywał się z xL (lub xL z xR) w kolejnym kroku iteracji. Jeżeli dodatkowo stworzymy zmienne przechowujące wcześniej liczone wartości funkcji to uda nam się ograniczyć liczbę wywołań funkcji o połowę. Opisana metoda to tak zwana metoda złotego podziału. Przykładowa implementacja wygląda następująco
def GoldenRatioRearch(func,xmin,xmax,args=(),xtol=0.01):
golden=0.5*(np.sqrt(5.0)-1.0)
xL=xmax-golden*(xmax-xmin)
xR=xmin+golden*(xmax-xmin)
fxL=func(xL,*args)
fxR=func(xR,*args)
while xmax-xmin>xtol:
if fxL<fxR:
xmin=xmin
xmax=xR
xR=xL
fxR=fxL
xL=xmax-golden*(xmax-xmin)
fxL=func(xL,*args)
else:
xmin=xL
xmax=xmax
xL=xR
fxL=fxR
xR=xmin+golden*(xmax-xmin)
fxR=func(xR,*args)
return 0.5*(xmax+xmin)
Napisanej metody optymalizacji możemy użyć w celu dopasowania funkcji do danych empirycznych metodą najmniejszych kwadratów. Przykład takiego zastosowania poniżej.
#suma kwadratów
def squares(a,func,xlist,ylist):
return sum([(func(xlist[i],*a)-ylist[i])**2 for i in range(len(xlist))])
#funkcja liniowa
def liniowa(x,a): return x*a
#generujemy przykladowe xlist
xlist=np.arange(0,1,0.001)
#generujemy wartosci funkcji z szumem
ylist=[liniowa(x,1.23)+0.000001*np.random.randn() for x in xlist]
#najlepsze dopasowanie metoda golden ration
print GoldenRatioRearch(squares,0,10,args=(liniowa,xlist,ylist),xtol=0.01)
Optymalizacja wielowymiarowa
Przejście od optymalizacji jedno- do wielowymiarowej fundamentalnie komplikuje problem. Pierwszym problemem jest istnienie tak zwanych punktów siodłowych. Nie istnieją zatem metody które zawsze znajdują szukane minimum, nawet jeżeli wiadomo że takie istnieje. Najpopularniejszą metodą jest downhill symplex lub inaczej metoda Neldera-Meada. Z powodu znacznego stopnia komplikacji nie będziemy jej samodzielnie implementować, a jedynie posłużymy się implementacją z biblioteki scipy.optimize. Dzięki niej możemy np. dopasowywać funkcję z więcej niż jednym parametrem do danych eksperymentalnych.
import scipy.optimize as so
#suma kwadratów
def squares(a,func,xlist,ylist):
return sum([(func(xlist[i],*a)-ylist[i])**2 for i in range(len(xlist))])
#funkcja liniowa
def liniowa(x,a,b): return x*a+b
#generujemy przykladowe xlist
xlist=np.arange(0,1,0.001)
#generujemy wartosci funkcji z szumem
ylist=[liniowa(x,1.23,-0.73)+0.000001*np.random.randn() for x in xlist]
#najlepsze dopasowanie metoda golden ration
print so.fmin(squares,(1,0),args=(liniowa,xlist,ylist))
Oczywiście dopasowywanie możemy przeprowadzać nie tylko metodą najmniejszych kwadratów.
Zadanie - rozkład Cauchy'ego
Wylosuj 10000 liczb z rozkładu Cauchy'ego z parametrami loc=1.23 i scale=2.0. Do wylosowanych danych dopasuj rozkład Cauche'ego trzema metodami
- METODA 1 - stwórz histogram otrzymanych wartości, znormalizuj go i metodą najmniejszych kwadratów dopasauj gęstość rozkładu do histogramu
- METODA 2 - dopasuj gęstość rozkładu do wylosowanych danych metodą największej wiarygodności
- METODA 3 - z wylosowanych danych stwórz dystrybuantę empiryczną. Metodą najmniejszych kwadratów dopasuj dystrybuantę rozkładu Cauchy'ego do dystrybuanty empirycznej.
Rozwiązanie
import scipy.optimize as so
def rho_cauchy(x,loc,scale):
return (np.pi*scale*(1.0+(x-loc)**2/(scale**2)))**(-1.0)
def F_cauchy(x,loc,scale):
return 0.5+np.arctan((x-loc)*1.0/scale)/np.pi
#losujemy 10000 liczb z rozkladu Cauchyego o loc=1.23 i scale=2.0
x=2*np.random.standard_cauchy(10000)+1.23
N=len(x)
#METODA 1 - Dopasowanie metoda najmniejszych kwadratow do histogramu
#tworzymy histogram
hist,bins= np.histogram(x,bins=np.linspace(-20,20,61))
#dlugosc przedzialu histogramowania
przedzial=bins[1]-bins[0]
#normalizujemy histogram aby moc go porownac z gestoscia
hist=hist*1.0/len(x)/przedzial
#liczymy wsp. srodkow przedzialow histogramowania
xhist=bins[:-1]+0.5*przedzial
#definiujemy sume kwadratow
def squares((loc,scale)):
return sum([(rho_cauchy(xhist[i],loc,scale)-hist[i])**2 for i in range(len(hist))])
#szukamy minimum funkcja fmin
fit1=tuple(so.fmin(squares,(0,1)))
print 'wynik metody1 to '+str(fit1)
#ogladamy wynik
py.plot(xhist,hist)
xtest=np.linspace(-20,20,1001)
ytest=[rho_cauchy(a,*fit1) for a in xtest]
py.plot(xtest,ytest)
py.show()
#METODA 2 - Metoda najwiekszej wiarygodnosci
#definiujemy -funkcje wiarygodnosci
def L((loc,scale)):
return -sum([np.log(rho_cauchy(a,loc,scale)) for a in x])
#szukamy minimum
fit2=tuple(so.fmin(L,(0,1)))
print 'wynik metody2 to '+str(fit2)
#METODA 3 - dopasowanie dystrybuant
xx=sorted(x)
yy=np.linspace(0,1,N)
#definiujemy funkcje KS bedaca maksimum z roznicy miedzy dystrybuanta empiryczna a teoretyczna
def KS((loc,scale)):
return max([abs(F_cauchy(xx[i],loc,scale)-yy[i]) for i in xrange(N)])
#szukamy minimum
fit3=tuple(so.fmin(KS,(0,1)))
print 'wynik metody3 to '+str(fit3)
#ogladamy wynik
cut=100
py.plot(xx[cut:-cut],yy[cut:-cut])
xtest=np.linspace(-20,20,1001)
ytest=[F_cauchy(x,*fit3) for x in xtest]
py.plot(xtest,ytest)
py.show()
Zadanie - Data Container
Napisz klasę funkcja przyjmującą w konstruktorze parametry funkcji i posiadającą reprezentację tekstową. Napisz dowolną funkcję dziedziczącą po klasie funkcja, której metoda call przyjmuje jeden argument i zwraca wartość funkcji dla podanego argumentu i parametrów podanych w konstruktorze. Napisz klasę DataContainer przyjmującą w konstruktorze dwie serie danych empirycznych o tej samej długości odpowiadające współrzędnym x i y. Obiekt klasy DataContainer powinien być wyposażony w metodę o nazwie fit, która przyjmuje jako argument obiekt klasy funkcja. Metoda fit powinna zwracać obiekt takiej samej klasy jak otrzymany w argumencie, ale z parametrami, dla których funkcja jest najlepiej (metodą najmniejszych kwadratów) dopasowana do przechowywanych w obiekcie danych.
Rozwiązanie
import numpy as np
import pylab as py
import time
import scipy.optimize as so
class funkcja(object):
def __init__(self,*args):
self.args=args
def __str__(self):
return 'to jest funkcja o nazwie '+self.__class__.__name__+' i argumentach '+str(self.args)
class liniowa(funkcja):
def __call__(self,x):
return self.args[0]*x*x+self.args[1]
class DataContainer(object):
def __init__(self,x,y):
self.x=np.array(x)
self.y=np.array(y)
self.n=len(x)
def __str__(self):
return '''to jest Data Container z danymi:
x[:10]:'''+str(self.x[:10])+'''
y[:10]:'''+str(self.y[:10])
def fit(self,funkcja):
parametry_poczatkowe=funkcja.args
def squares(parametry):
funkcja.__init__(*tuple(parametry))
return sum((map(funkcja,self.x)-self.y)**2)
parametry_dopasowane=so.fmin(squares,parametry_poczatkowe)
funkcja.__init__(*tuple(parametry_dopasowane))
return funkcja
#generujemy przykladowe xlist
xlist=np.arange(0,1,0.001)
#generujemy wartosci funkcji z szumem
f=liniowa(1.23,-0.73)
ylist=[f(x)+0.05*np.random.randn() for x in xlist]
d=DataContainer(xlist,ylist)
f=liniowa(1,2)
f=d.fit(f)
py.plot(d.x,d.y)
py.plot(d.x,map(f,d.x))
py.show()