Laboratorium EEG/Analiza czas-częstość w matlabie: Różnice pomiędzy wersjami
m (→Implementacja) |
m (→Zadanie 3) |
||
| (Nie pokazano 34 wersji utworzonych przez 3 użytkowników) | |||
| Linia 1: | Linia 1: | ||
[[Laboratorium_EEG]]/Czas-częstość | [[Laboratorium_EEG]]/Czas-częstość | ||
| − | = | + | [https://drive.google.com/open?id=0BzwQ_Lscn8yDRlBmOGRoVkEydEE paczka z materiałami do pierwszej części ćwiczeń] |
| + | |||
[http://www.fuw.edu.pl/~suffa/LabEEG/TF.zip Moduł czas-częstość w Matlabie] | [http://www.fuw.edu.pl/~suffa/LabEEG/TF.zip Moduł czas-częstość w Matlabie] | ||
| − | + | =Zasada nieoznaczoności dla przestrzeni czas-częstość= | |
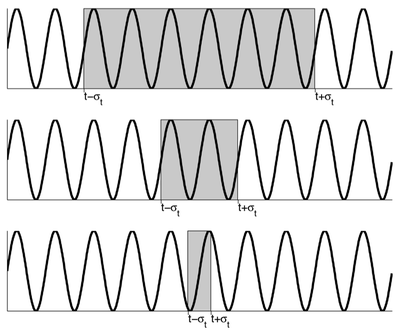
Poniższy rysunek obrazuje koncepcję zasady nieoznaczoności w przypadku analizy czas-częstość: im dokładniej znamy lokalizację interesującego nas fragmentu sygnału (struktury) w czasie tym mniej dokładnie możemy poznać jego częstość. | Poniższy rysunek obrazuje koncepcję zasady nieoznaczoności w przypadku analizy czas-częstość: im dokładniej znamy lokalizację interesującego nas fragmentu sygnału (struktury) w czasie tym mniej dokładnie możemy poznać jego częstość. | ||
| Linia 17: | Linia 18: | ||
: <math>\sigma_t^2 = \frac{1}{E_x}\int_{-\infty}^{\infty} (t - t_0)^2 |x(t)|^2 dt </math> | : <math>\sigma_t^2 = \frac{1}{E_x}\int_{-\infty}^{\infty} (t - t_0)^2 |x(t)|^2 dt </math> | ||
| − | Analogicznie w dziedzinie częstości: | + | Analogicznie w dziedzinie częstości (tu traktujemy gęstość widmową mocy jak gęstość prawdopodobieństwa): |
: <math>f_0 = \frac{1}{E_x} \int_{-\infty}^{\infty}f |X(f)|^2 df</math> | : <math>f_0 = \frac{1}{E_x} \int_{-\infty}^{\infty}f |X(f)|^2 df</math> | ||
| Linia 25: | Linia 26: | ||
: <math>\sigma_t^2 \sigma_f^2 \ge \frac{1}{16 \pi^2}</math> | : <math>\sigma_t^2 \sigma_f^2 \ge \frac{1}{16 \pi^2}</math> | ||
| − | + | =Estymatory gęstości widmowej dla przestrzeni czas-częstość= | |
Energię sygnału w jednej z dziedzin, czasu bądź częstości, możemy policzyć tak: | Energię sygnału w jednej z dziedzin, czasu bądź częstości, możemy policzyć tak: | ||
: <math> E_x=\int_{-\infty}^{\infty}{|x(t)|^2 dt} = \int_{-\infty}^{\infty}{|X(f)|^2 df}</math> | : <math> E_x=\int_{-\infty}^{\infty}{|x(t)|^2 dt} = \int_{-\infty}^{\infty}{|X(f)|^2 df}</math> | ||
| Linia 35: | Linia 36: | ||
: <math> \int_{-\infty}^{\infty}{\rho_x(t,f) df} = |x(t)|^2</math> | : <math> \int_{-\infty}^{\infty}{\rho_x(t,f) df} = |x(t)|^2</math> | ||
| − | + | ==Dystrybucja energii== | |
Podobnie jak widmo mocy, gęstość energii fizycznego sygnału nie może być obliczona, może być jedynie estymowana. W celu estymacji gęstości energii można posłużyć się dwuwymiarowymi dystrybucjami energii. | Podobnie jak widmo mocy, gęstość energii fizycznego sygnału nie może być obliczona, może być jedynie estymowana. W celu estymacji gęstości energii można posłużyć się dwuwymiarowymi dystrybucjami energii. | ||
Jedną z podstawowych dystrybucji jest dystrybucja Wigner-Ville'a (WVD): | Jedną z podstawowych dystrybucji jest dystrybucja Wigner-Ville'a (WVD): | ||
| Linia 42: | Linia 43: | ||
: <math> W_x(t,f) = \int_{-\infty}^{\infty} X(f+\xi/2)X^*(f-\xi/2) e^{i 2 \pi \xi t} d\xi</math> | : <math> W_x(t,f) = \int_{-\infty}^{\infty} X(f+\xi/2)X^*(f-\xi/2) e^{i 2 \pi \xi t} d\xi</math> | ||
| − | + | ===Implementacja=== | |
Przykładowa implementacja WVD dla sygnału rzeczywistego: | Przykładowa implementacja WVD dla sygnału rzeczywistego: | ||
| Linia 74: | Linia 75: | ||
{{hidden end}} | {{hidden end}} | ||
| − | + | '''Wersja w Matlabie''' | |
<source lang = matlab> | <source lang = matlab> | ||
function [Tfr,ts,f]=tf_wvd(x,Fs,varargin) | function [Tfr,ts,f]=tf_wvd(x,Fs,varargin) | ||
| Linia 109: | Linia 110: | ||
</source> | </source> | ||
| − | + | ===Własności=== | |
Własności WVD: | Własności WVD: | ||
* zachowanie energii | * zachowanie energii | ||
| Linia 119: | Linia 120: | ||
: <math> y(t)=\sqrt{k}x(kt) \Rightarrow W_y(t,f) = W_x(kt, f/k)</math> | : <math> y(t)=\sqrt{k}x(kt) \Rightarrow W_y(t,f) = W_x(kt, f/k)</math> | ||
| − | + | ===Wyrazy mieszane=== | |
| − | WVD jest reprezentacją kwadratową więc: | + | WVD jest reprezentacją kwadratową — dekompozycja sumy sygnałów nie jest sumą ich dekopozycji. Mamy więc: |
: <math> y(t) = x_1(t)+x_2(t) \Rightarrow W_y(t, f) = W_{x_1}(t, f)+W_{x_2}(t, f)+W_{x_1,x_2}(t, f)+W_{x_2,x_1}(t, f)</math> | : <math> y(t) = x_1(t)+x_2(t) \Rightarrow W_y(t, f) = W_{x_1}(t, f)+W_{x_2}(t, f)+W_{x_1,x_2}(t, f)+W_{x_2,x_1}(t, f)</math> | ||
gdzie | gdzie | ||
: <math> W_{x_1,x_2}(t, f) = \int_{-\infty}^{\infty} x_1(t+\tau/2)x_2^*(t-\tau/2)e^{-i 2 \pi f \tau} d\tau</math> | : <math> W_{x_1,x_2}(t, f) = \int_{-\infty}^{\infty} x_1(t+\tau/2)x_2^*(t-\tau/2)e^{-i 2 \pi f \tau} d\tau</math> | ||
| − | + | ===Rozdzielczość=== | |
* idealnie dla chirpów liniowych (sygnał o liniowo zmieniającej się częstości chwilowej): | * idealnie dla chirpów liniowych (sygnał o liniowo zmieniającej się częstości chwilowej): | ||
| Linia 161: | Linia 162: | ||
| − | * struktura wyrazów mieszanych: zaobserwuj, że niezależnie od tego jak bardzo odseparowane są struktury w przestrzeni czas-częstość pomiędzy nimi powstają wyrazy mieszane. Zauważ, że wyrazy mieszane mają wysoką częstość przestrzennej zmienności. | + | * struktura wyrazów mieszanych: zaobserwuj, że niezależnie od tego jak bardzo odseparowane są struktury w przestrzeni czas-częstość, pomiędzy nimi powstają wyrazy mieszane. Zauważ, że wyrazy mieszane mają wysoką częstość przestrzennej zmienności. |
{{hidden begin|title=wersja w pythonie}} | {{hidden begin|title=wersja w pythonie}} | ||
| Linia 197: | Linia 198: | ||
pcolor(linspace(0,ts(end),size(Tfr,2)),linspace(0,f(end),size(Tfr,1)),real(Tfr)); shading interp;</source> | pcolor(linspace(0,ts(end),size(Tfr,2)),linspace(0,f(end),size(Tfr,1)),real(Tfr)); shading interp;</source> | ||
| − | + | ==Klasa Cohena== | |
| − | + | WVD jest najprostszym elementem klasy Cohena — klasy kwadratowych rozkładów energii w dziedzinie czas-częstość, niezmienniczych przy translacjach czasu i częstości. | |
| − | WVD jest najprostszym elementem klasy Cohena. | ||
Ponieważ wyrazy mieszane mają wysoką częstość przestrzenną w płaszczyźnie czas-częstość to można je częściowo zniwelować poprzez zastosowanie odpowiedniego filtra. Koncepcja ta jest wykorzystywana w klasie Cohena. | Ponieważ wyrazy mieszane mają wysoką częstość przestrzenną w płaszczyźnie czas-częstość to można je częściowo zniwelować poprzez zastosowanie odpowiedniego filtra. Koncepcja ta jest wykorzystywana w klasie Cohena. | ||
Ogólnie klasę tę można zapisać jako: | Ogólnie klasę tę można zapisać jako: | ||
| Linia 206: | Linia 206: | ||
: <math> \Pi(t,f) = \int_{-\infty}^{\infty}\int_{-\infty}^{\infty} f(\xi, \tau) e^{-i 2 \pi (f\tau + \xi t)} dt df</math> | : <math> \Pi(t,f) = \int_{-\infty}^{\infty}\int_{-\infty}^{\infty} f(\xi, \tau) e^{-i 2 \pi (f\tau + \xi t)} dt df</math> | ||
Najczęściej <math> \Pi</math> wybiera się jako pewną funkcję gładzącą — w zależności od tego wyboru będziemy mieli w różnym stopniu osłabiane wyrazy mieszane. | Najczęściej <math> \Pi</math> wybiera się jako pewną funkcję gładzącą — w zależności od tego wyboru będziemy mieli w różnym stopniu osłabiane wyrazy mieszane. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Krótkoczasowa transformacja Fouriera i spektrogram== | ==Krótkoczasowa transformacja Fouriera i spektrogram== | ||
| Linia 249: | Linia 213: | ||
: <math>F_x(t,f; h)= \int_{-\infty}^{\infty}{x(u) h^*(u-t)e^{- i 2 \pi u f} du} </math> | : <math>F_x(t,f; h)= \int_{-\infty}^{\infty}{x(u) h^*(u-t)e^{- i 2 \pi u f} du} </math> | ||
| − | + | ===Własności=== | |
Jeśli okienko ma skończoną energię to STFT jest transformacją odwracalną i można odzyskać z niej sygnał w reprezentacji czasowej: | Jeśli okienko ma skończoną energię to STFT jest transformacją odwracalną i można odzyskać z niej sygnał w reprezentacji czasowej: | ||
: <math> x(t) = \frac{1}{E_h}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}F_x(u,f;h)h(t-u)e^{i 2\pi t f}\,du\,df </math> | : <math> x(t) = \frac{1}{E_h}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}F_x(u,f;h)h(t-u)e^{i 2\pi t f}\,du\,df </math> | ||
| Linia 255: | Linia 219: | ||
Tak więc sygnał może być rozłożony na liniową kombinację elementarnych falek-„atomów” postaci: | Tak więc sygnał może być rozłożony na liniową kombinację elementarnych falek-„atomów” postaci: | ||
: <math>h_{t,f}(u)=h(u-t)e^{i 2 \pi f u}</math> | : <math>h_{t,f}(u)=h(u-t)e^{i 2 \pi f u}</math> | ||
| − | Każdy atom uzyskiwany jest przez translację pojedynczego okna | + | Każdy atom uzyskiwany jest przez translację pojedynczego okna ''h'' w czasie i jego modulację częstością ''f''. |
===Spektrogram=== | ===Spektrogram=== | ||
| Linia 574: | Linia 538: | ||
* Proszę zbadać rozdzielczość czasową spektrogramu posługując się funkcją delta oraz rozdzielczość częstotliwościową posługując się funkcją sinus (Trzeba „przeskanować” czas funkcją delta, a częstości sinusem). Proszę wykonać to dla kilku długości okienek ''h''. | * Proszę zbadać rozdzielczość czasową spektrogramu posługując się funkcją delta oraz rozdzielczość częstotliwościową posługując się funkcją sinus (Trzeba „przeskanować” czas funkcją delta, a częstości sinusem). Proszę wykonać to dla kilku długości okienek ''h''. | ||
* Proszę zbadać rozdzielczość spektrogramu przy pomocy dwóch funkcji Gabora, dla różnych ich odległości w czasie i w częstości. Zaobserwować strukturę wyrazów mieszanych. | * Proszę zbadać rozdzielczość spektrogramu przy pomocy dwóch funkcji Gabora, dla różnych ich odległości w czasie i w częstości. Zaobserwować strukturę wyrazów mieszanych. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| Linia 731: | Linia 638: | ||
end</source> | end</source> | ||
| − | === | + | ==Matching pursuit (MP) — dopasowanie kroczące== |
| + | ===Definicja=== | ||
| + | Dopasowanie kroczące (ang. ''matching pursuit'', MP) jest procedurą polegającą na rozłożeniu sygnału <math>s(t)</math> na funkcje składowe <math>g_{\gamma_n}</math> pochodzące z określonego zbioru funkcji <math>D</math> (tzw. słownika). Słowniki wykorzystywane w metodach czas-częstość często składają się z funkcji Gabora tj. funkcji sinus modulowanej funkcją Gaussa. MP jest algorytmem iteracyjnym. W pierwszym kroku wybierana jest funkcja dająca największy iloczyn skalarny z sygnałem. W każdym następnym kroku funkcja jest analogicznie dopasowywana do residuum sygnału, pozostałego po odjęciu wyniku poprzedniej iteracji. | ||
| + | |||
| + | Formalnie wygląda to następująco: | ||
| + | : <math> | ||
| + | \left \{ | ||
| + | \begin{array}{l} | ||
| + | R^0s = s\\ | ||
| + | R^ns = \langle R^ns,g_{\gamma_n} \rangle g_{\gamma_n}+R^{n+1}s\\ | ||
| + | g_{\gamma_n} = \arg \max_{g_{\gamma_i} \in D } |\langle R^ns, g_{\gamma_i}\rangle| | ||
| + | \end{array} | ||
| + | \right . | ||
| + | </math> | ||
| + | gdzie: | ||
| + | <math>\arg \max_{g_{\gamma_i} \in D }</math> oznacza tego <math> g_{\gamma_i}</math>, który daje największy iloczyn skalarny z aktualnym residuum: <math>|\langle R^ns, g_{\gamma_i}\rangle|</math>. | ||
| + | |||
| + | Słowniki mogą być dowolne, ale najczęściej składamy je z funkcji Diraca, sinus i Gabora: | ||
| + | : <math> | ||
| + | g_\gamma (t) = K(\gamma)e^{ -\pi\left( \frac{t-u}{\sigma} \right)^2} | ||
| + | \sin\left(2 \pi f (t-u)+\phi\right) | ||
| + | </math> | ||
| + | normalizacja <math> K(\gamma)</math> jest taka, że <math> ||g_{\gamma}||=1</math>, <math>\gamma=\{ u, f, \sigma, | ||
| + | \phi \}</math> to parametry funkcji w słowniku (<math>u</math> — translacja w czasie, <math> f</math> — częstość, <math> \sigma</math> — szerokość w czasie, <math> \phi</math> — faza). | ||
| + | |||
| + | ===Dystrybucja energii=== | ||
| + | Reprezentację czas-częstość uzyskujemy z dekompozycji MP sumując dystrybucje WVD pojedynczych atomów: | ||
| + | : <math> | ||
| + | W_{ g_{\gamma_n}}(t, f)=\int g_{\gamma_n} \bigl (t + \frac{\tau}{2} \bigr)\; | ||
| + | g_{\gamma_n}^*\left(t- \frac{\tau}{2} \right) e^{- i 2 \pi f \tau } d \tau | ||
| + | </math> | ||
| + | |||
| + | : <math> | ||
| + | E^{MP} = \sum_{n=0}^M |\langle R^n s, \;g_{\gamma_n} \rangle|^2 \; W_{g_{\gamma_n}} (t, f) | ||
| + | </math> | ||
| + | |||
| + | W wyrażeniu tym nie ma wyrazów mieszanych :-) | ||
| + | |||
| + | |||
| + | |||
| − | |||
<!-- | <!-- | ||
[https://brain.fuw.edu.pl/~suffa/LabEEG/mp.tar.gz Moduł czas-częstość metodą MP] | [https://brain.fuw.edu.pl/~suffa/LabEEG/mp.tar.gz Moduł czas-częstość metodą MP] | ||
| Linia 749: | Linia 694: | ||
*Do definicji ścieżek w Matlabie dołączyć katalog z pakietem MP. | *Do definicji ścieżek w Matlabie dołączyć katalog z pakietem MP. | ||
*Uruchomić skrypt <tt>example.m</tt> w celu przetestowania działania programu MP. | *Uruchomić skrypt <tt>example.m</tt> w celu przetestowania działania programu MP. | ||
| + | --> | ||
| − | + | Implementacja MP, jest dostępna bezpośrednio w środowisku Matlab, jako plugin do EEGLAB. Program można pobrać ze strony [git.nimitz.pl/mp-eeglab-plugin.git/snapshot/18ad395338572078632297cd071ba5e925b7b22e.tar.gz], jednak wygodniejsze wydaje się bezpośrednie skopiowanie repozytorium. W tym celu należy: | |
*otworzyć terminal, | *otworzyć terminal, | ||
*przejść do folderu, gdzie zainstalowany został EEGLAB, | *przejść do folderu, gdzie zainstalowany został EEGLAB, | ||
| Linia 758: | Linia 704: | ||
Po ponownym uruchomieniu EEGLABa, MP będzie dostępne w zakładce <i>tools</i>. Wynik działania skryptu zapisywany jest do struktury BOOK. Przed wykonaniem kolejnych obliczeń, należy zapisać wyniki poprzednich. W przeciwnym razie zostaną one nadpisane. Do programu dołączone zostały stosowne narzędzia wizualizujące wyniki. | Po ponownym uruchomieniu EEGLABa, MP będzie dostępne w zakładce <i>tools</i>. Wynik działania skryptu zapisywany jest do struktury BOOK. Przed wykonaniem kolejnych obliczeń, należy zapisać wyniki poprzednich. W przeciwnym razie zostaną one nadpisane. Do programu dołączone zostały stosowne narzędzia wizualizujące wyniki. | ||
| − | + | =Ćwiczenia= | |
| − | + | == Zadanie 1 == | |
| − | |||
| − | |||
<!-- | <!-- | ||
* Ściągnąć pakiet plików Matlaba do analizy czas-częstość: | * Ściągnąć pakiet plików Matlaba do analizy czas-częstość: | ||
https://brain.fuw.edu.pl/~suffa/LabEEG/TF.zip | https://brain.fuw.edu.pl/~suffa/LabEEG/TF.zip | ||
--> | --> | ||
| − | + | * Zapoznać się z implementacją matlabową analiz czas-częstość. | |
* Zapoznać się z opisem metod czas-częstość, wykonując polecenia opisane przy każdej z metod. | * Zapoznać się z opisem metod czas-częstość, wykonując polecenia opisane przy każdej z metod. | ||
* Zbadać własności metod czas-częstość, m.in.: | * Zbadać własności metod czas-częstość, m.in.: | ||
| Linia 773: | Linia 717: | ||
** Proszę zbadać strukturę wyrazów mieszanych w sposób analogiczny jak było to pokazane dla spektrogramu. | ** Proszę zbadać strukturę wyrazów mieszanych w sposób analogiczny jak było to pokazane dla spektrogramu. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ==Zadanie 2 == | |
Korzystając z danych SSVEP zebranych podczas zajęć w semestrze zimowym: | Korzystając z danych SSVEP zebranych podczas zajęć w semestrze zimowym: | ||
| − | * | + | * Wytnij odcinki sygnałów zbierane dla tych samych częstości stymulacji, zostawiając przed i po sygnale okres referencyjny (np. 2 s). |
| − | * | + | * Sprawdź poprawność wycięcia danych: uśrednij odcinki sygnałów zbierane dla tych samych częstości stymulacji i obejrzyj uśrednione dane z kanału zawierającego sygnał bodźca. |
| − | * Wykonać analizę czas-częstość posługując się pakietem EEGLAB. | + | * Przefiltruj odcinki filtrami dolno- i górnoprzepustowym o częstościach odcięcia odpowiednio 1 Hz i 45 Hz. Uśrednij przefiltrowane odcinki. |
| + | * Wybierz kanał, na którym odpowiedź SSVEP była najsilniejsza. Obejrzyj uśredniony odcinek danych. Czy widać odpowiedź w wybranej częstości? | ||
| + | * Wykonaj mapy czas-częstość dla wybranego kanału oraz dla kanału bodźca za pomocą: | ||
| + | ** spektrogramu, | ||
| + | ** korzystając z reprezentacji falek Morleta, | ||
| + | ** korzystając z reprezentacji falek Wignera-Villa. | ||
| + | * Powtórz analizę wykonując mapy czas-częstość dla każdego odcinka danych osobno i uśredniając uzyskane mapy. | ||
| + | * Wykonaj mapy ERD/ERS dla wybranego kanału. | ||
| + | <!-- | ||
| + | * Wykonać analizę czas-częstość posługując się pakietem EEGLAB. W tym celu: | ||
| + | ** przefiltrować dane SSVEP (ciągłe) w paśmie 1-45 Hz filtrem Butterwortha rzędu 1; | ||
| + | ** wczytać je do EEGLABa - dane należy umieścić w strukturze EEG.data, oraz wypełnić pozostałe pola tej struktury, w szczególności pola EEG.event, tak aby była możliwość wybrania tych realizacji eksperymentu, które były stymulowane określoną częstością; | ||
| + | ** dla wybranej „dobrej” częstości i najlepszego kanału wykonać dekompozycję MP na dwa sposoby: | ||
| + | *** dla pojedynczych realizacji; | ||
| + | *** dla uśrednionego sygnału. | ||
| + | *** Uwaga: te dekompozycje robimy na odcinkach wyciętych od 1 s przed rozpoczęciem do 1 s po zakończeniu stymulacji. | ||
| + | ** Obejrzeć mapy czas-częstość. | ||
| + | ** Czy w każdej realizacji widać SSVEP? | ||
| + | ** Czy SSVEP w pojedynczych realizacjach jest spójną oscylacją? | ||
| + | |||
| + | |||
Rysunki poniżej przedstawiają przykład analizy danych EEG zebranych podczas stymulacji SSVEP o częstości 15 Hz. | Rysunki poniżej przedstawiają przykład analizy danych EEG zebranych podczas stymulacji SSVEP o częstości 15 Hz. | ||
[[Plik:eeglab_ssvep1.png|200px|left]][[Plik:eeglab_ssvep2.png|200px]] | [[Plik:eeglab_ssvep1.png|200px|left]][[Plik:eeglab_ssvep2.png|200px]] | ||
| + | --> | ||
| − | + | == Zadanie 3 == | |
Pobrać plik z danymi: | Pobrać plik z danymi: | ||
| − | + | http://www.fuw.edu.pl/~suffa/LabEEG/Characterize_ch4_F50_G4.mat | |
Opis danych: | Opis danych: | ||
dane zawierają zapisy z lokalnych potencjałów polowych (LFP) z kory czuciowej małpy podczas podawania bodźca wibracyjnego do palca. | dane zawierają zapisy z lokalnych potencjałów polowych (LFP) z kory czuciowej małpy podczas podawania bodźca wibracyjnego do palca. | ||
| − | Macierz zawiera 50 powtórzeń po 3 sekundy. Częstość próbkowania wynosi 5000 Hz. Bodziec podawany był pomiędzy 1 a 2 sekundą. | + | Macierz zawiera 50 powtórzeń po 3 sekundy. Częstość próbkowania wynosi 5000 Hz. Bodziec podawany był pomiędzy 1. a 2. sekundą. |
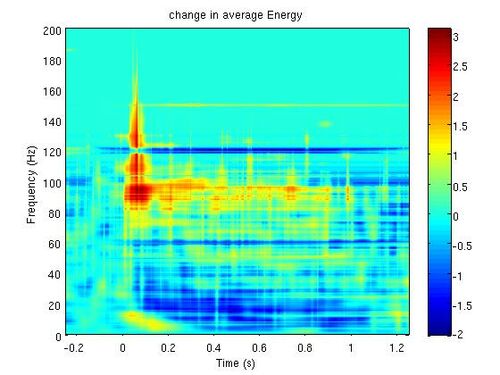
| − | [[Plik:MP_LFP_13_02.jpg|500px|thumb| | + | [[Plik:MP_LFP_13_02.jpg|500px|thumb|center|<figure id="fig:1"/> Analiza zapisów LFP z kory czuciowej małpy podczas podawania bodźca wibracyjnego do palca, o częstości 50 Hz. Mapa czas-częstość przedstawia względną gęstość energii (w skali dB) względem okresu referencyjnego 200-50 ms przed początkiem stymulacji. Dane opisane są w pracy: Supratim Ray, Steven S. Hsiao, Nathan E. Crone, Piotr J. Franaszczuk, and Ernst Niebur. Effect of Stimulus Intensity on the Spike—Local Field Potential Relationship in the Secondary Somatosensory Cortex. The Journal of Neuroscience, 2008, 28(29):7334-7343.]] |
Zadania do wykonania: | Zadania do wykonania: | ||
| − | * Otrzymać mapy czas-częstość dla pojedynczych realizacji a następnie uśrednić je po realizacjach. | + | * Otrzymać mapy czas-częstość dla pojedynczych realizacji za pomocą ciągłej transformacji falkowej (sklaogramy) a następnie uśrednić je po realizacjach. |
* Na średniej mapie poszukać występowania odpowiedzi w częstościach high-gamma (100-200 Hz). | * Na średniej mapie poszukać występowania odpowiedzi w częstościach high-gamma (100-200 Hz). | ||
* W przypadku braku widocznej odpowiedzi, rozważyć następujące operacje: | * W przypadku braku widocznej odpowiedzi, rozważyć następujące operacje: | ||
| − | ** usunąć częstości sieci (60 Hz i wyższe harmoniczne); | + | ** usunąć częstości sieci (60 Hz i wyższe harmoniczne) filtrem pasmowo zaporowym; |
** zastosować logarytmiczną skalę energii; | ** zastosować logarytmiczną skalę energii; | ||
| − | ** policzyć zmiany gęstości energii względem jej wartości w okresie referencyjnym. | + | ** policzyć zmiany gęstości energii względem jej wartości w okresie referencyjnym - okres referencyjny wybrać na podstawie średniego skalogramu. |
Mapa czas-częstość średniej gęstości energii otrzymaną metodą Matching Pursuit jest przedstawiona na <xr id="fig:1">rys. %i</xr>. | Mapa czas-częstość średniej gęstości energii otrzymaną metodą Matching Pursuit jest przedstawiona na <xr id="fig:1">rys. %i</xr>. | ||
{{clear}} | {{clear}} | ||
| − | + | ==Zadanie 4 == | |
| − | Wykonać analizę metodą MP dla danych z zadania | + | Wykonać analizę metodą MP dla danych z zadania 2. |
| − | + | =Literatura= | |
S. Mallat and Z. Zhang (1993) Matching pursuit with time-frequency dictionaries. IEEE Transactions on Signal Processing, 41:3397-3415. | S. Mallat and Z. Zhang (1993) Matching pursuit with time-frequency dictionaries. IEEE Transactions on Signal Processing, 41:3397-3415. | ||
Aktualna wersja na dzień 09:09, 1 kwi 2020
Laboratorium_EEG/Czas-częstość
paczka z materiałami do pierwszej części ćwiczeń
Moduł czas-częstość w Matlabie
Spis treści
- 1 Zasada nieoznaczoności dla przestrzeni czas-częstość
- 2 Estymatory gęstości widmowej dla przestrzeni czas-częstość
- 3 Ćwiczenia
- 4 Literatura
Zasada nieoznaczoności dla przestrzeni czas-częstość
Poniższy rysunek obrazuje koncepcję zasady nieoznaczoności w przypadku analizy czas-częstość: im dokładniej znamy lokalizację interesującego nas fragmentu sygnału (struktury) w czasie tym mniej dokładnie możemy poznać jego częstość.
Zasadę tą można wyrazić formalnie w następujący sposób. Potraktujmy moc sygnału [math]x(t)[/math] (o skończonej energii) jak rozkład zmiennej losowej. Aby rozkład był unormowany trzeba podzielić go przez energię sygnału: [math]E_x = \int_{-\infty}^{\infty} |x(t)|^2 dt \lt \infty[/math]. Zatem rozkład ten jest postaci: [math]p(t) = \frac{1}{E_x}|x(t)|^2 [/math].
Jako lokalizację występowania sygnału w czasie przyjmujemy średnie położenie jego energii:
- [math]t_0 = \frac{1}{E_x} \int_{-\infty}^{\infty}t |x(t)|^2 dt[/math]
zaś jako miarę skupienia energii wokół tego położenia przyjmujemy wariancję:
- [math]\sigma_t^2 = \frac{1}{E_x}\int_{-\infty}^{\infty} (t - t_0)^2 |x(t)|^2 dt [/math]
Analogicznie w dziedzinie częstości (tu traktujemy gęstość widmową mocy jak gęstość prawdopodobieństwa):
- [math]f_0 = \frac{1}{E_x} \int_{-\infty}^{\infty}f |X(f)|^2 df[/math]
- [math]\sigma_f^2 = \frac{1}{E_x}\int_{-\infty}^{\infty} (f - f_0)^2 |X(f)|^2 df [/math]
Można pokazać (np. Pinsky, 2002), że iloczyn wariancji energii w czasie i w częstości jest ograniczony od dołu:
- [math]\sigma_t^2 \sigma_f^2 \ge \frac{1}{16 \pi^2}[/math]
Estymatory gęstości widmowej dla przestrzeni czas-częstość
Energię sygnału w jednej z dziedzin, czasu bądź częstości, możemy policzyć tak:
- [math] E_x=\int_{-\infty}^{\infty}{|x(t)|^2 dt} = \int_{-\infty}^{\infty}{|X(f)|^2 df}[/math]
i interpretujemy [math]|x(t)|^2[/math] albo [math]|X(f)|^2[/math] jako gęstości energii. Stąd pomysł, żeby rozszerzyć tą koncepcję na obie dziedziny jednocześnie i wprowadzić pojęcie gęstości energii w dziedzinie czas-częstość [math]\rho_x(t,f)[/math]:
- [math] E_x=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}{\rho_x(t,f) dt df}[/math]
muszą też być spełnione własności brzegowe:
- [math] \int_{-\infty}^{\infty}{\rho_x(t,f) dt}=|X(f)|^2[/math]
- [math] \int_{-\infty}^{\infty}{\rho_x(t,f) df} = |x(t)|^2[/math]
Dystrybucja energii
Podobnie jak widmo mocy, gęstość energii fizycznego sygnału nie może być obliczona, może być jedynie estymowana. W celu estymacji gęstości energii można posłużyć się dwuwymiarowymi dystrybucjami energii. Jedną z podstawowych dystrybucji jest dystrybucja Wigner-Ville'a (WVD):
- [math] W_x(t,f)=\int_{-\infty}^{\infty}x(t+\tau/2)x^*(t-\tau/2)e^{-i 2 \pi f \tau} d\tau[/math]
lub
- [math] W_x(t,f) = \int_{-\infty}^{\infty} X(f+\xi/2)X^*(f-\xi/2) e^{i 2 \pi \xi t} d\xi[/math]
Implementacja
Przykładowa implementacja WVD dla sygnału rzeczywistego:
import numpy as np
import pylab as py
import scipy.signal as ss
def wvd(x, Fs, plot=True):
samples = len(x)
N = samples / 2
z = np.zeros(samples)
xh = ss.hilbert(x)
x_period_h = np.concatenate((z,xh,z));
t = range(0, samples, 1) # czas w samplach
tfr = np.zeros((samples , samples), dtype=complex)
for ti in t:
for tau in range(-samples/2,samples/2):
tfr[samples/2 + tau, ti] = x_period_h[samples+ti + tau] * x_period_h[samples+ti - tau].conj()
tfr = np.fft.fftshift(tfr,axes = 0)
Tfr = np.fft.fft(tfr, samples, axis=0)/samples
ts = np.array(t, dtype=float) / (float(Fs))
f = np.linspace(0, Fs / 2, N)
if plot:
py.imshow( Tfr.real, interpolation='nearest', extent=[0, ts[-1], 0, f[-1]], origin='lower', aspect='auto')
py.show()
return Tfr, ts, f
Wersja w Matlabie
function [Tfr,ts,f]=tf_wvd(x,Fs,varargin)
doplot = true;
switch nargin
case 0:1
disp('tf_wvd - not enough input arguments');
return
case 2
otherwise
doplot=varargin{1};
end
x = hilbert(x);
samples = length(x);
N = floor(samples/2);
t = 0:samples; t(end)= [];
tfr = zeros(N,samples);
for ti=t
for tau=0:min(ti,samples-ti)-1
tfr(tau+1,ti+1) = x(ti+tau+1).*conj(x(ti-tau+1));
end
end
Tfr = fft(tfr,samples,1);
ts = t./Fs;
f = linspace(0,Fs/2,N);
if doplot
pcolor(linspace(0,ts(end),size(Tfr,2)),linspace(0,f(end),size(Tfr,1)),real(Tfr)); shading interp;
end
Własności
Własności WVD:
- zachowanie energii
- własności brzegowe
- zachowywanie przesunięcia w czasie i w częstości
- [math] y(t) = x(t-t_0) \Rightarrow W_y(t,f) = W_x(t-t_0,f)[/math]
- [math] y(t) = x(t)e^{i 2 \pi f_0 t} \Rightarrow W_y(t,f) = W_x(t,f-f_0)[/math]
- zachowywanie skalowania
- [math] y(t)=\sqrt{k}x(kt) \Rightarrow W_y(t,f) = W_x(kt, f/k)[/math]
Wyrazy mieszane
WVD jest reprezentacją kwadratową — dekompozycja sumy sygnałów nie jest sumą ich dekopozycji. Mamy więc:
- [math] y(t) = x_1(t)+x_2(t) \Rightarrow W_y(t, f) = W_{x_1}(t, f)+W_{x_2}(t, f)+W_{x_1,x_2}(t, f)+W_{x_2,x_1}(t, f)[/math]
gdzie
- [math] W_{x_1,x_2}(t, f) = \int_{-\infty}^{\infty} x_1(t+\tau/2)x_2^*(t-\tau/2)e^{-i 2 \pi f \tau} d\tau[/math]
Rozdzielczość
- idealnie dla chirpów liniowych (sygnał o liniowo zmieniającej się częstości chwilowej):
import tf as tf
import pylab as py
Fs = 512.0
T = 1.0
t = tf.czas(T,Fs)
ch = tf.chirp(5,Fs/2-5,T,Fs)
Tfr,ts,f = tf.wvd(ch,Fs,False)
py.subplot(2,1,1)
py.plot(t,ch)
py.subplot(2,1,2)
py.imshow(Tfr.real,interpolation= 'nearest',extent=[0,ts[-1],0,f[-1]],origin='lower',aspect='auto')
py.show()
Wersja w Matlabie
Fs = 512.0;
T = 1.0;
t = tf_czas(T,Fs);
ch = tf_chirp(5,Fs/2-5,T,Fs);
[Tfr,ts,f] = tf_wvd(ch,Fs,false);
subplot(2,1,1)
plot(t,ch)
subplot(2,1,2)
pcolor(linspace(0,ts(end),size(Tfr,2)),linspace(0,f(end),size(Tfr,1)),real(Tfr)); shading interp;
- struktura wyrazów mieszanych: zaobserwuj, że niezależnie od tego jak bardzo odseparowane są struktury w przestrzeni czas-częstość, pomiędzy nimi powstają wyrazy mieszane. Zauważ, że wyrazy mieszane mają wysoką częstość przestrzennej zmienności.
import tf as tf
import pylab as py
Fs = 512.0
T = 1.0
t = tf.czas(T,Fs)
s1 = tf.gabor(t0=0.3, sigma = 0.05, T = 1.0, f=100, phi = 0,Fs=Fs)
s2 = tf.gabor(t0=0.7, sigma = 0.05, T = 1.0, f=200, phi = 0,Fs=Fs)
s = s1 + s2
Tfr,ts,f = tf.wvd(s,Fs,False)
py.subplot(2,1,1)
py.plot(t,s)
py.subplot(2,1,2)
py.imshow(Tfr.real,interpolation= 'nearest',extent=[0,ts[-1],0,f[-1]],origin='lower',aspect='auto')
py.show()
Wersja w Matlabie
Fs = 512.0;
T = 1.0;
t = tf_czas(T,Fs);
s1 = tf_gabor(0.3, 0.05, 1.0, 100, 0, Fs);
s2 = tf_gabor(0.7, 0.05, 1.0, 200, 0, Fs);
s = s1 + s2;
[Tfr,ts,f] = tf_wvd(s,Fs,false);
subplot(2,1,1)
plot(t,s)
subplot(2,1,2)
pcolor(linspace(0,ts(end),size(Tfr,2)),linspace(0,f(end),size(Tfr,1)),real(Tfr)); shading interp;
Klasa Cohena
WVD jest najprostszym elementem klasy Cohena — klasy kwadratowych rozkładów energii w dziedzinie czas-częstość, niezmienniczych przy translacjach czasu i częstości. Ponieważ wyrazy mieszane mają wysoką częstość przestrzenną w płaszczyźnie czas-częstość to można je częściowo zniwelować poprzez zastosowanie odpowiedniego filtra. Koncepcja ta jest wykorzystywana w klasie Cohena. Ogólnie klasę tę można zapisać jako:
- [math] C_x(t,f,\Pi) = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} \Pi(s-t, \xi - f) W_x(s,\xi) ds d\xi[/math]
gdzie
- [math] \Pi(t,f) = \int_{-\infty}^{\infty}\int_{-\infty}^{\infty} f(\xi, \tau) e^{-i 2 \pi (f\tau + \xi t)} dt df[/math]
Najczęściej [math] \Pi[/math] wybiera się jako pewną funkcję gładzącą — w zależności od tego wyboru będziemy mieli w różnym stopniu osłabiane wyrazy mieszane.
Krótkoczasowa transformacja Fouriera i spektrogram
Definicja krótkoczasowej transformacji Fouriera
Krótkoczasowa transformacja Fouriera (ang. short-time Fourier transform, STFT) może być rozumiana jako seria transformacji Fouriera wykonanych na sygnale podzielonym na okienka, przy czym położenie okienka w czasie jest w ramach takiej serii przesuwane monotonicznie. W wersji ciągłej możemy to zapisać tak:
- [math]F_x(t,f; h)= \int_{-\infty}^{\infty}{x(u) h^*(u-t)e^{- i 2 \pi u f} du} [/math]
Własności
Jeśli okienko ma skończoną energię to STFT jest transformacją odwracalną i można odzyskać z niej sygnał w reprezentacji czasowej:
- [math] x(t) = \frac{1}{E_h}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}F_x(u,f;h)h(t-u)e^{i 2\pi t f}\,du\,df [/math]
gdzie [math]E_h=\int_{-\infty}^{\infty}|h(t)|^2\,dt [/math] Tak więc sygnał może być rozłożony na liniową kombinację elementarnych falek-„atomów” postaci:
- [math]h_{t,f}(u)=h(u-t)e^{i 2 \pi f u}[/math]
Każdy atom uzyskiwany jest przez translację pojedynczego okna h w czasie i jego modulację częstością f.
Spektrogram
Definicja
Spektrogram: kwadrat modułu STFT jest estymatą gęstości energii w przestrzeni czas-częstość:
- [math]S_x(t, f) =\left|\int_{-\infty}^{\infty}{x(u) h^*(u - t) e^{-i 2\pi f u} du}\right|^2[/math]
Implementacja
- Spektrogram zaiplementowany jest w pythonie w module matplotlib.pyplot jako funkcja specgram (dokumentacja).
- W matlabie spectrogram jest zaimplementowany w signal procesing toolbox:
Własności
Przesunięcia
Spektrogram zachowuje przesunięcie:
w czasie
- [math]y(t) = x(t - t_0)\Rightarrow S_y(t, f; h) = S_x(t - t_0, f; h)[/math]
import matplotlib.pyplot as py
from tf import czas, gabor
import numpy as np
import scipy.signal as ss
# parametry
t0 = 1.0
sigma = 0.1
T = 4.0
f = 10
phi = 0
Fs = 128.0
NFFT = int(Fs)
sig1 = gabor(t0, sigma, T, f, phi, Fs) # sygnał
sig2 = gabor(t0 + 2, sigma, T, f, phi, Fs) # sygnał przesunięty w czasie
py.subplot(221)
h = ss.hamming(NFFT)
sig1_padded = (np.concatenate((np.zeros(NFFT/2),sig1,np.zeros(NFFT/2))))
P,f,t,im1 = py.specgram(sig1_padded,NFFT = len(h),Fs = Fs,window = h, noverlap = NFFT-1, sides = 'onesided')
py.imshow(P,aspect='auto',origin='lower',extent=(t[0]-(NFFT/2)/Fs,t[-1]-(NFFT/2)/Fs,f[0],f[-1]),interpolation='nearest')
py.subplot(222)
sig2_padded = (np.concatenate((np.zeros(NFFT/2),sig2,np.zeros(NFFT/2))))
P,f,t,im2 = py.specgram(sig2_padded,NFFT = len(h),Fs = Fs,window = h, noverlap = NFFT-1, sides = 'onesided')
py.imshow(P,aspect='auto',origin='lower',extent=(t[0]-(NFFT/2)/Fs,t[-1]-(NFFT/2)/Fs,f[0],f[-1]),interpolation='nearest')
py.subplot(223)
time = czas(T, Fs)
py.plot(time,sig1)
py.subplot(224)
py.plot(time ,sig2)
py.show()
Wersja w Matlabie
% parametry
t0 = 1.0;
sigma = 0.1;
T = 4.0;
f = 10;
phi = 0;
Fs = 128.0;
NFFT = floor(Fs);
sig1 = tf_gabor(t0, sigma, T, f, phi, Fs);
% sygnał
sig2 = tf_gabor(t0 + 2, sigma, T, f, phi, Fs);
% sygnał przesunięty w czasie
subplot(2,2,1);
sig1_padded = [zeros(1,floor(NFFT/2)), sig1, zeros(1,floor(NFFT/2))];
P=spectrogram(sig1_padded,NFFT,NFFT-1,NFFT,Fs);
pcolor(linspace(0,T,size(P,2)),linspace(0,Fs/2,size(P,1)),abs(P)); shading interp;
subplot(2,2,2)
sig2_padded = [zeros(1,floor(NFFT/2)), sig2, zeros(1,floor(NFFT/2))];
P=spectrogram(sig2_padded,NFFT,NFFT-1,NFFT,Fs);
pcolor(linspace(0,T,size(P,2)),linspace(0,Fs/2,size(P,1)),abs(P)); shading interp;
subplot(2,2,3)
time = tf_czas(T, Fs);
plot(time,sig1);
subplot(2,2,4)
plot(time ,sig2);
i w częstości:
- [math]y(t) = x(t) e ^{i 2 \pi f_0 t}\Rightarrow S_y(t, f; h) = S_x(t, f - f_0; h)[/math]
import matplotlib.pyplot as py
from tf import czas, gabor
import numpy as np
import scipy.signal as ss
# parametry
t0 = 1.0
sigma = 0.1
T = 4.0
f = 10
phi = 0
Fs = 128.0
NFFT = int(Fs)
time = czas(T, Fs)
sig1 = gabor(t0, sigma, T, f, phi, Fs) # sygnał
sig2 = gabor(t0, sigma, T, f+20, phi, Fs)# sygnał przesunięty w częstości
py.subplot(221)
h = ss.hamming(NFFT)
sig1_padded = (np.concatenate((np.zeros(NFFT/2),sig1,np.zeros(NFFT/2))))
P,f,t,im1 = py.specgram(sig1_padded,NFFT = len(h),Fs = Fs,window = h, noverlap = NFFT-1, sides = 'onesided')
py.imshow(P,aspect='auto',origin='lower',extent=(t[0]-(NFFT/2)/Fs,t[-1]-(NFFT/2)/Fs,f[0],f[-1]),interpolation='nearest')
py.subplot(222)
sig2_padded = (np.concatenate((np.zeros(NFFT/2),sig2,np.zeros(NFFT/2))))
P,f,t,im2 = py.specgram(sig2_padded,NFFT = len(h),Fs = Fs,window = h, noverlap = NFFT-1, sides = 'onesided')
py.imshow(P,aspect='auto',origin='lower',extent=(t[0]-(NFFT/2)/Fs,t[-1]-(NFFT/2)/Fs,f[0],f[-1]),interpolation='nearest')
py.subplot(223)
py.plot(time,sig1)
py.subplot(224)
py.plot(time ,sig2)
py.show()
Wersja w Matlabie
% parametry
t0 = 1.0;
sigma = 0.1;
T = 4.0;
f = 10;
phi = 0;
Fs = 128.0;
NFFT = floor(Fs);
time = tf_czas(T, Fs);
sig1 = tf_gabor(t0, sigma, T, f, phi, Fs);
% sygnał
sig2 = tf_gabor(t0, sigma, T, f+20, phi, Fs);
% sygnał przesunięty w częstości
subplot(2,2,1);
sig1_padded = [zeros(1,floor(NFFT/2)),sig1,zeros(1,floor(NFFT/2))];
P=spectrogram(sig1_padded,NFFT,NFFT-1,NFFT,Fs);
pcolor(linspace(0,T,size(P,2)),linspace(0,Fs/2,size(P,1)),abs(P)); shading interp;
subplot(2,2,2)
sig2_padded = [zeros(1,floor(NFFT/2)),sig2,zeros(1,floor(NFFT/2))];
P=spectrogram(sig2_padded,NFFT,NFFT-1,NFFT,Fs);
pcolor(linspace(0,T,size(P,2)),linspace(0,Fs/2,size(P,1)),abs(P)); shading interp;
subplot(2,2,3)
plot(time,sig1);
subplot(2,2,4)
plot(time ,sig2);
Wyrazy mieszane
Spektrogram jest reprezentacją kwadratową. Spektrogram sumy sygnałów nie jest sumą spektrogramów sygnałów składowych, jest tam jeszcze coś:
- [math]y(t) = x_1(t)+x_2(t) \Rightarrow S_y(t, f) = S_{x_1}(t, f)+S_{x_2}(t, f)+S_{x_1,x_2}(t, f)+S_{x_2,x_1}(t, f)[/math]
gdzie
- [math]S_{x_1,x_2}(t, f) = F_{x_1}(t, f)F^*_{x_2}(t, f)[/math]
Jak mogą wyglądać wyrazy mieszane ilustruje poniższy kod. Kolejne subploty pokazują spektrogramy uzyskane dla sygnału będącego sumą dwóch funkcji Gabora o częstościach różniących się o 2 Hz i położeniach różniących się o kolejne wielokrotności 0,1 s.
import matplotlib.pyplot as py
from tf import czas, gabor
import numpy as np
import scipy.signal as ss
# parametry
t0 = 1.0
sigma = 0.05
T = 2.0
f0 = 20
phi = 0
Fs = 128.0
NFFT = int(Fs)
time = czas(T, Fs)
h = ss.hamming(NFFT)
for i in range(9):
py.subplot(3,3,i+1)
sig1 = gabor(t0, sigma, T, f0, phi, Fs) # sygnal
sig2 = gabor(t0+i*0.1, sigma, T, f0+2, phi, Fs)# sygnał przesunięty w częstości o 2 Hz i w czasie o i*0.1 s
sig1_padded = (np.concatenate((np.zeros(NFFT/2),sig1,np.zeros(NFFT/2))))
sig2_padded = (np.concatenate((np.zeros(NFFT/2),sig2,np.zeros(NFFT/2))))
P,f,t,im1 = py.specgram(sig1_padded+sig2_padded,NFFT = len(h),Fs = Fs,window = h, noverlap = NFFT-1, sides = 'onesided')
py.imshow(P,aspect='auto',origin='lower',extent=(t[0]-(NFFT/2)/Fs,t[-1]-(NFFT/2)/Fs,f[0],f[-1]),interpolation='nearest')
py.show()
Wersja w Matlabie
% parametry
t0 = 1.0;
sigma = 0.05;
T = 2.0;
f0 = 20;
phi = 0;
Fs = 128.0;
NFFT = floor(Fs);
time = tf_czas(T, Fs);
for i=0:8
subplot(3,3,i+1)
sig1 = tf_gabor(t0, sigma, T, f0, phi, Fs); % sygnal
sig2 = tf_gabor(t0+i*0.1, sigma, T, f0+2, phi, Fs);
% sygnał przesunięty w częstości o 2 Hz i w czasie o i*0.1 s
sig1_padded = [zeros(1,floor(NFFT/2)),sig1,zeros(1,floor(NFFT/2))];
sig2_padded = [zeros(1,floor(NFFT/2)),sig2,zeros(1,floor(NFFT/2))];
P=spectrogram(sig1_padded+sig2_padded,NFFT,NFFT-1,NFFT,Fs);
pcolor(linspace(0,T,size(P,2)),linspace(0,Fs/2,size(P,1)),abs(P)); shading interp;
end
Wyrazy mieszane występują także w przypadku pojedynczej struktury dla sygnału rzeczywistego. „Mieszające się” obiekty to energia zlokalizowana w dodatniej i ujemnej części widma częstości. Efekt jest stosunkowo słaby i uwidacznia się dopiero na mapach czas-częstość logarytmu gęstości energii. Problem ten można obejść stosując transformację Hilberta, gdyż po tej transformacji cała energia skupiona jest w dodatniej części widma. Własność tę ilustruje poniższy program:
from matplotlib.pyplot import specgram, plot, subplot, show, imshow
from tf import czas, gabor
from numpy import pi, log
from scipy.signal import hamming, hilbert
# parametry
t0 = 0.5
sigma = 0.1
T = 1.0
f = 30
phi = 0
Fs = 256.0
s = gabor(t0, sigma, T, f, phi, Fs)
t = czas(T, Fs)
subplot(411)
plot(t,s)
subplot(412)
h = hamming(32)
NFFT =len(h)
P,f,t,im1 = specgram(s,NFFT = len(h),Fs = Fs,window = h, noverlap = 31,sides = 'twosided')
imshow(P,aspect='auto',origin='lower',extent=(t[0]-(NFFT/2)/Fs,t[-1]-(NFFT/2)/Fs,f[0],f[-1]),interpolation='nearest')
subplot(413)
imshow(log(P),aspect='auto',origin='lower',extent=(t[0]-(NFFT/2)/Fs,t[-1]-(NFFT/2)/Fs,f[0],f[-1]),interpolation='nearest')
subplot(414)
s_ana = hilbert(s) # sygnał analityczny
P,f,t,im2 = specgram(s_ana,NFFT = len(h),Fs = Fs,window = h, noverlap = 31, sides = 'twosided')
imshow(log(P),aspect='auto',origin='lower',extent=(t[0]-(NFFT/2)/Fs,t[-1]-(NFFT/2)/Fs,f[0],f[-1]),interpolation='nearest')
show()
Wersja w Matlabie
% parametry
t0 = 0.5;
sigma = 0.1;
T = 1.0;
f = 30;
phi = 0;
Fs = 256.0;
NFFT = 32;
Fs2 = floor(Fs/2);
s = tf_gabor(t0, sigma, T, f, phi, Fs);
t = tf_czas(T, Fs);
f = linspace(-Fs2,Fs2,NFFT+1); f(end) = [];
subplot(4,1,1)
plot(t,s);
subplot(4,1,2)
P=spectrogram(s,NFFT,NFFT-1,f,Fs);
pcolor(linspace(0,T,size(P,2)),linspace(f(1),f(end),size(P,1)),abs(P)); shading interp;
subplot(4,1,3)
pcolor(linspace(0,T,size(P,2)),linspace(f(1),f(end),size(P,1)),log(abs(P))); shading interp;
subplot(4,1,4)
s_ana = hilbert(s); % sygnał analityczny
P=spectrogram(s_ana,NFFT,NFFT-1,f,Fs);
pcolor(linspace(0,T,size(P,2)),linspace(f(1),f(end),size(P,1)),log(abs(P))); shading interp;
Ćwiczenie:
- Proszę zbadać rozdzielczość czasową spektrogramu posługując się funkcją delta oraz rozdzielczość częstotliwościową posługując się funkcją sinus (Trzeba „przeskanować” czas funkcją delta, a częstości sinusem). Proszę wykonać to dla kilku długości okienek h.
- Proszę zbadać rozdzielczość spektrogramu przy pomocy dwóch funkcji Gabora, dla różnych ich odległości w czasie i w częstości. Zaobserwować strukturę wyrazów mieszanych.
Ciągła transformata falkowa i skalogram
Ciągłą transformata falkowa
Definicja
Ciągła transformacja falkowa (ang. Continuous Wavelet Transform, CWT) dana jest wzorem:
- [math] P_x(t,a;\Psi)= \int_{-\infty}^{\infty}{x(s)\Psi^*_{t,a}(s) ds}[/math]
gdzie
- [math] \Psi_{t,a}(s) = \frac{1}{\sqrt{|a|}} \Psi\left(\frac{s-t}{a}\right)[/math]
a jest skalą. Od falki [math]\Psi[/math] wymagamy żeby miała średnią 0.
Transformację tę można interpretować jako rzutowanie sygnału na kolejne wersje falki [math]\Psi[/math] przesunięte o t i przeskalowane o a.
Inne spojrzenie na transformację falkową uwidacznia się gdy połączymy dwa powyższe wzory:
- [math]P_x(t,a;\Psi)= \frac{1}{\sqrt{|a|}}\int_{-\infty}^{\infty}{x(s) \Psi^*\left(\frac{s-t}{a}\right) ds} [/math]
Tu widać, że dla ustalonej skali a transformacja falkowa jest splotem sygnału z falką o skali a. Ten sposób myślenia o transformacji falkowej umożliwia zastosowanie szybkiego algorytmu obliczeniowego bazującego na tym, że splot w dziedzinie czasu odpowiada mnożeniu w dziedzinie częstości.
Skalogram
Podobnie jak dla STFT i spektrogramu, możemy dla CWT wprowadzić pojęcie skalogramu, będącego estymatą gęstości energii w przestrzeni czas-skala.
- [math]S_x(t,a;\Psi)=\left| P_x(t,a;\Psi)\right|^2[/math]
Dla falek, które są dobrze skupione wokół częstości [math]f_0[/math] dla skali [math]a_0=1[/math] można wprowadzić utożsamienie [math]f=\frac{f_0}{a}[/math]. Utożsamienie to pozwala przekształcić reprezentację czas-skala w reprezentację czas-częstość:
- [math]S_x(t,f;\Psi)=\left| P_x(t,f_0/f;\Psi)\right|^2[/math]
Implementacja
Przykładowa implementacja obliczania skalogramu dla falek Morleta przedstawiona jest poniżej. Korzysta ona z własności splotu.
def cwt(x, MinF,MaxF,Fs,w=7.0,df =1.0,plot = True):
'''w - parametr falki Morleta,
wiąże się z jej częstościa centralną i skalą w następujacy sposób:
f = 2*a*w / T
gdzie: a-skala, T-długość sygnału w sek.'''
T= len(x)/Fs
M = len(x)
t = np.arange(0,T,1./Fs)
freqs = np.arange(MinF,MaxF,df)
P = np.zeros((len(freqs),M))
X = np.fft.fft(x) # transformacja sygnału do dziedziny czestosci
for i,f in enumerate(freqs): # petla po kolejnych czestosciach
a = T*f/(2*w) # obliczenie skali dla danej czestosci
psi = np.fft.fft(ss.morlet(M, w=w, s=a, complete=True)) # transformacja falki Morleta do dziedziny czestosci. W bardziej wydajnym kodzie moznaby zastosowac analityczna postac tej falki w dziedzinie czestosci.
psi /= np.sqrt(np.sum(psi*psi.conj())) # normalizacja energii falki
CWT = np.fft.fftshift(ss.ifft(X*psi))
P[i,:] = (CWT*CWT.conj()).real
if plot:
py.imshow(P,aspect='auto',origin='lower',extent=(0,T,MinF, MaxF))
py.show()
return P,f,t
Wersja w Matlabie
function [P,f,t]=tf_cwt(x,MinF,MaxF,Fs,varargin)
w = 7;
df = 1;
doplot = true;
switch nargin
case 0:3
disp('tf_cwt - not enough input arguments');
return
case 4
case 5
w=varargin{1};
case 2
w=varargin{1};
df=varargin{2};
otherwise
w=varargin{1};
df=varargin{2};
doplot=varargin{3};
end
T = length(x)/Fs;
M = length(x);
t = 0:1/Fs:T; t(end) = [];
freqs = MinF:df:MaxF; freqs(end) = [];
P = zeros(length(freqs),M);
X = fft(x);
for i=1:length(freqs)
f = freqs(i);
s = T*f/(2*w);
psi = fft(tf_morlet(M,w,s,true));
psi = psi./sqrt(sum(abs(psi).^2));
tmp = fftshift(ifft(X.*psi));
P(i,:) = abs(tmp).^2;
end
if doplot
pcolor(linspace(0,T,size(P,2)),linspace(MinF,MaxF,size(P,1)),P); shading interp;
end
Matching pursuit (MP) — dopasowanie kroczące
Definicja
Dopasowanie kroczące (ang. matching pursuit, MP) jest procedurą polegającą na rozłożeniu sygnału [math]s(t)[/math] na funkcje składowe [math]g_{\gamma_n}[/math] pochodzące z określonego zbioru funkcji [math]D[/math] (tzw. słownika). Słowniki wykorzystywane w metodach czas-częstość często składają się z funkcji Gabora tj. funkcji sinus modulowanej funkcją Gaussa. MP jest algorytmem iteracyjnym. W pierwszym kroku wybierana jest funkcja dająca największy iloczyn skalarny z sygnałem. W każdym następnym kroku funkcja jest analogicznie dopasowywana do residuum sygnału, pozostałego po odjęciu wyniku poprzedniej iteracji.
Formalnie wygląda to następująco:
- [math] \left \{ \begin{array}{l} R^0s = s\\ R^ns = \langle R^ns,g_{\gamma_n} \rangle g_{\gamma_n}+R^{n+1}s\\ g_{\gamma_n} = \arg \max_{g_{\gamma_i} \in D } |\langle R^ns, g_{\gamma_i}\rangle| \end{array} \right . [/math]
gdzie: [math]\arg \max_{g_{\gamma_i} \in D }[/math] oznacza tego [math] g_{\gamma_i}[/math], który daje największy iloczyn skalarny z aktualnym residuum: [math]|\langle R^ns, g_{\gamma_i}\rangle|[/math].
Słowniki mogą być dowolne, ale najczęściej składamy je z funkcji Diraca, sinus i Gabora:
- [math] g_\gamma (t) = K(\gamma)e^{ -\pi\left( \frac{t-u}{\sigma} \right)^2} \sin\left(2 \pi f (t-u)+\phi\right) [/math]
normalizacja [math] K(\gamma)[/math] jest taka, że [math] ||g_{\gamma}||=1[/math], [math]\gamma=\{ u, f, \sigma, \phi \}[/math] to parametry funkcji w słowniku ([math]u[/math] — translacja w czasie, [math] f[/math] — częstość, [math] \sigma[/math] — szerokość w czasie, [math] \phi[/math] — faza).
Dystrybucja energii
Reprezentację czas-częstość uzyskujemy z dekompozycji MP sumując dystrybucje WVD pojedynczych atomów:
- [math] W_{ g_{\gamma_n}}(t, f)=\int g_{\gamma_n} \bigl (t + \frac{\tau}{2} \bigr)\; g_{\gamma_n}^*\left(t- \frac{\tau}{2} \right) e^{- i 2 \pi f \tau } d \tau [/math]
- [math] E^{MP} = \sum_{n=0}^M |\langle R^n s, \;g_{\gamma_n} \rangle|^2 \; W_{g_{\gamma_n}} (t, f) [/math]
W wyrażeniu tym nie ma wyrazów mieszanych :-)
Implementacja MP, jest dostępna bezpośrednio w środowisku Matlab, jako plugin do EEGLAB. Program można pobrać ze strony [git.nimitz.pl/mp-eeglab-plugin.git/snapshot/18ad395338572078632297cd071ba5e925b7b22e.tar.gz], jednak wygodniejsze wydaje się bezpośrednie skopiowanie repozytorium. W tym celu należy:
- otworzyć terminal,
- przejść do folderu, gdzie zainstalowany został EEGLAB,
- odnaleźć katalog plugins i przejść do niego,
- wpisać komendę: git clone git://git.nimitz.pl/mp-eeglab-plugin.git.
Po ponownym uruchomieniu EEGLABa, MP będzie dostępne w zakładce tools. Wynik działania skryptu zapisywany jest do struktury BOOK. Przed wykonaniem kolejnych obliczeń, należy zapisać wyniki poprzednich. W przeciwnym razie zostaną one nadpisane. Do programu dołączone zostały stosowne narzędzia wizualizujące wyniki.
Ćwiczenia
Zadanie 1
- Zapoznać się z implementacją matlabową analiz czas-częstość.
- Zapoznać się z opisem metod czas-częstość, wykonując polecenia opisane przy każdej z metod.
- Zbadać własności metod czas-częstość, m.in.:
- Proszę przyjrzeć się definicjom transformaty falkowej i STFT i opowiedzieć o analogiach i różnicach.
- Proszę zbadać własności przesunięć w czasie i w częstości dla skalogramu w sposób analogiczny jak było to pokazane dla spektrogramu.
- Proszę zbadać strukturę wyrazów mieszanych w sposób analogiczny jak było to pokazane dla spektrogramu.
Zadanie 2
Korzystając z danych SSVEP zebranych podczas zajęć w semestrze zimowym:
- Wytnij odcinki sygnałów zbierane dla tych samych częstości stymulacji, zostawiając przed i po sygnale okres referencyjny (np. 2 s).
- Sprawdź poprawność wycięcia danych: uśrednij odcinki sygnałów zbierane dla tych samych częstości stymulacji i obejrzyj uśrednione dane z kanału zawierającego sygnał bodźca.
- Przefiltruj odcinki filtrami dolno- i górnoprzepustowym o częstościach odcięcia odpowiednio 1 Hz i 45 Hz. Uśrednij przefiltrowane odcinki.
- Wybierz kanał, na którym odpowiedź SSVEP była najsilniejsza. Obejrzyj uśredniony odcinek danych. Czy widać odpowiedź w wybranej częstości?
- Wykonaj mapy czas-częstość dla wybranego kanału oraz dla kanału bodźca za pomocą:
- spektrogramu,
- korzystając z reprezentacji falek Morleta,
- korzystając z reprezentacji falek Wignera-Villa.
- Powtórz analizę wykonując mapy czas-częstość dla każdego odcinka danych osobno i uśredniając uzyskane mapy.
- Wykonaj mapy ERD/ERS dla wybranego kanału.
Zadanie 3
Pobrać plik z danymi: http://www.fuw.edu.pl/~suffa/LabEEG/Characterize_ch4_F50_G4.mat
Opis danych: dane zawierają zapisy z lokalnych potencjałów polowych (LFP) z kory czuciowej małpy podczas podawania bodźca wibracyjnego do palca. Macierz zawiera 50 powtórzeń po 3 sekundy. Częstość próbkowania wynosi 5000 Hz. Bodziec podawany był pomiędzy 1. a 2. sekundą.
Zadania do wykonania:
- Otrzymać mapy czas-częstość dla pojedynczych realizacji za pomocą ciągłej transformacji falkowej (sklaogramy) a następnie uśrednić je po realizacjach.
- Na średniej mapie poszukać występowania odpowiedzi w częstościach high-gamma (100-200 Hz).
- W przypadku braku widocznej odpowiedzi, rozważyć następujące operacje:
- usunąć częstości sieci (60 Hz i wyższe harmoniczne) filtrem pasmowo zaporowym;
- zastosować logarytmiczną skalę energii;
- policzyć zmiany gęstości energii względem jej wartości w okresie referencyjnym - okres referencyjny wybrać na podstawie średniego skalogramu.
Mapa czas-częstość średniej gęstości energii otrzymaną metodą Matching Pursuit jest przedstawiona na rys. 1.
Zadanie 4
Wykonać analizę metodą MP dla danych z zadania 2.
Literatura
S. Mallat and Z. Zhang (1993) Matching pursuit with time-frequency dictionaries. IEEE Transactions on Signal Processing, 41:3397-3415.
Pinsky, Mark (2002), Introduction to Fourier Analysis and Wavelets, Brooks/Cole, ISBN 0-534-37660-6
Laboratorium_EEG/Czas-częstość