Laboratorium EEG/CSP: Różnice pomiędzy wersjami
m (→Formalizm) |
|||
| (Nie pokazano 47 pośrednich wersji utworzonych przez tego samego użytkownika) | |||
| Linia 4: | Linia 4: | ||
[https://brain.fuw.edu.pl/edu/images/2/2f/BSS.pdf slajdy z prezentacji] | [https://brain.fuw.edu.pl/edu/images/2/2f/BSS.pdf slajdy z prezentacji] | ||
| − | =Ślepa separacja źródeł= | + | =Ślepa separacja źródeł (BSS)= |
| + | {{hidden begin|title=Wstęp teoretyczny do BSS}} | ||
Rozważmy ''N''-kanałowy sygnał EEG. | Rozważmy ''N''-kanałowy sygnał EEG. | ||
Próbkę tego sygnału możemy przedstawić jako punkt w przestrzeni rozpiętej przez osie, z których każda reprezentuje wartość potencjału w jednym kanale. Cały sygnał tworzy w tej przestrzeni chmurę punktów. Rozciągłość tej chmury w danym kierunku mówi nam o wariancji (zmienności) sygnału w tym kierunku. | Próbkę tego sygnału możemy przedstawić jako punkt w przestrzeni rozpiętej przez osie, z których każda reprezentuje wartość potencjału w jednym kanale. Cały sygnał tworzy w tej przestrzeni chmurę punktów. Rozciągłość tej chmury w danym kierunku mówi nam o wariancji (zmienności) sygnału w tym kierunku. | ||
| Linia 51: | Linia 52: | ||
: <math>J(w) = \frac{w^T C_T w}{w^T C_{NT} w} </math> | : <math>J(w) = \frac{w^T C_T w}{w^T C_{NT} w} </math> | ||
Ekstremum tego ilorazu można znaleźć poprzez policzenie gradientu <math>J(w)</math> i przyrównanie go do zera: | Ekstremum tego ilorazu można znaleźć poprzez policzenie gradientu <math>J(w)</math> i przyrównanie go do zera: | ||
| − | :<math> \nabla J(w) = \frac{ 2 C_{T} w \left(w^T C_{NT} w\right) | + | :<math> \nabla J(w) = \frac{ 2 C_{T} w \left(w^T C_{NT} w\right) -2C_{NT} w \left(w^T C_{T} w \right)}{\left(w^T C_{NT} w\right)^2} = \frac{ 2}{w^T C_{NT} w}\left[ C_{T}w -\frac{w^T C_{T} w}{w^T C_{NT} w} C_{NT} w \right]</math> |
| − | |||
| − | |||
| − | |||
Przyrównując to wyrażenie do zera dostajemy do rozwiązania tzw. uogólnione zagadnienie własne: | Przyrównując to wyrażenie do zera dostajemy do rozwiązania tzw. uogólnione zagadnienie własne: | ||
:<math> C_{T}w =\frac{w^T C_{T} w}{w^T C_{NT} w} C_{NT} w </math> | :<math> C_{T}w =\frac{w^T C_{T} w}{w^T C_{NT} w} C_{NT} w </math> | ||
| Linia 60: | Linia 58: | ||
Aby znaleźć <math> \lambda</math> i <math>w</math> możemy wykorzystać w Matlabie funkcję <tt>eig</tt>. Funkcja ta rozwiązuje (również) uogólnione zagadnienia własne postaci ''Aw''=λ''Bw'' dostarczając w wyniku macierz wektorów własnych (w kolumnach) oraz macierz zawierającą na przekątnej odpowiadające im wartości własne. | Aby znaleźć <math> \lambda</math> i <math>w</math> możemy wykorzystać w Matlabie funkcję <tt>eig</tt>. Funkcja ta rozwiązuje (również) uogólnione zagadnienia własne postaci ''Aw''=λ''Bw'' dostarczając w wyniku macierz wektorów własnych (w kolumnach) oraz macierz zawierającą na przekątnej odpowiadające im wartości własne. | ||
| + | {{hidden end}} | ||
<!-- | <!-- | ||
| Linia 93: | Linia 92: | ||
--> | --> | ||
| − | ===Ćwiczenie symulacyjne === | + | ====Ćwiczenie symulacyjne ==== |
{{hidden begin|title=kod przykładowy}} | {{hidden begin|title=kod przykładowy}} | ||
<source lang = matlab> | <source lang = matlab> | ||
| Linia 188: | Linia 187: | ||
title('ilustracja sytuacji pomiarowej -\newline znane są potencjały na elektrodach w dwóch warunkach eksperymentalnych') | title('ilustracja sytuacji pomiarowej -\newline znane są potencjały na elektrodach w dwóch warunkach eksperymentalnych') | ||
subplot(2,2,3); | subplot(2,2,3); | ||
| − | plot(t(baseline_ind),(squeeze(X(:, | + | plot(t(baseline_ind),(squeeze(X(:,2,baseline_ind)))','b'); hold on |
plot(t(ERP_ind),(squeeze( X(:,2,ERP_ind)))','r'); hold off | plot(t(ERP_ind),(squeeze( X(:,2,ERP_ind)))','r'); hold off | ||
xlabel('elektroda 2') | xlabel('elektroda 2') | ||
| Linia 241: | Linia 240: | ||
==Zastosowanie filtra CSP do detekcji potencjału P300== | ==Zastosowanie filtra CSP do detekcji potencjału P300== | ||
| + | {{hidden begin|title=Eksperyment}} | ||
===Eksperyment=== | ===Eksperyment=== | ||
* Proszę zapoznać się z instrukcją: http://laboratorium-eeg.braintech.pl/rozdz10.html | * Proszę zapoznać się z instrukcją: http://laboratorium-eeg.braintech.pl/rozdz10.html | ||
| Linia 287: | Linia 287: | ||
# Danych z kalibracji potrzebować będziemy kilka zestawów. Proszę powtórzyć kilkukrotnie scenariusz „kalibracjaP300”. Przed każdym uruchomieniem trzeba zmienić string w pliku <tt>file_id_name</tt> np. na <tt>test???</tt> gdzie <tt>???</tt> oznacza kolejne numery. | # Danych z kalibracji potrzebować będziemy kilka zestawów. Proszę powtórzyć kilkukrotnie scenariusz „kalibracjaP300”. Przed każdym uruchomieniem trzeba zmienić string w pliku <tt>file_id_name</tt> np. na <tt>test???</tt> gdzie <tt>???</tt> oznacza kolejne numery. | ||
--> | --> | ||
| − | + | {{hidden end}} | |
===Analiza wstępna=== | ===Analiza wstępna=== | ||
Poszczególne etapy analizy proszę kodować w osobnych funkcjach. Funkcje te powinny być wywoływane z nadrzędnego skryptu, który powinien umożliwic wykoanie całości analiz. | Poszczególne etapy analizy proszę kodować w osobnych funkcjach. Funkcje te powinny być wywoływane z nadrzędnego skryptu, który powinien umożliwic wykoanie całości analiz. | ||
* Wczytać dane kalibracyjne do Matlaba i pociąć je na realizacje typu T — „target” (związane z wystąpieniami litery „B”) i NT — „non-target” (pozostałe litery) o długości −200 do +800 ms wokół triggerów. Dla każdej realizacji odjąć trend liniowy. | * Wczytać dane kalibracyjne do Matlaba i pociąć je na realizacje typu T — „target” (związane z wystąpieniami litery „B”) i NT — „non-target” (pozostałe litery) o długości −200 do +800 ms wokół triggerów. Dla każdej realizacji odjąć trend liniowy. | ||
| − | * Sygnał zmontować wzgl. „połączonych uszu” i wyświetlić średnie przebiegi dla warunku T i NT w układzie topograficznym — wykorzystać w tym celu | + | * Sygnał zmontować wzgl. „połączonych uszu” i wyświetlić średnie przebiegi dla warunku T i NT w układzie topograficznym — można wykorzystać w tym celu poniższy fragment kodu. |
| + | {{hidden begin|title= fragment kodu do rysowania dwóch ERPów -- zamiast funkcji plottopo}} | ||
| + | <source lang = matlab> | ||
| + | %% stworzenie osi | ||
| + | % zakładam, że dane do rysowania są w dwóch strukturach EEG1 i EEG2 (struktury eeglab), | ||
| + | % te dane są podzielone na realizacje i mają kształt (kanały , czas, epoki) | ||
| + | % i że mamy już załadowane położenia elektrod we współrzędnych | ||
| + | % biegunowych | ||
| + | w = 0.125; | ||
| + | h = 0.125; | ||
| + | sc = 0.8; | ||
| + | figure() | ||
| + | for chanNum = 1:length(EEG1.chanlocs) | ||
| + | r =EEG1.chanlocs(chanNum).radius; | ||
| + | theta = EEG1.chanlocs(chanNum).theta; | ||
| + | x = r* sin(theta/180*pi)*sc+0.46; | ||
| + | y = r* cos(theta/180*pi)*sc+0.46; | ||
| + | ax(chanNum) = axes('Position', [x, y, w, h]); | ||
| + | end | ||
| + | %%uśredniam EEG po powtórzeniach aby otrzymać ERP | ||
| + | ERP1 =squeeze( mean( EEG1.data,3)) ; | ||
| + | ERP2 =squeeze( mean( EEG2.data,3)) ; | ||
| + | %% rysowanie uśrednionych potencjałów z dwóch struktur EEG | ||
| + | for chanNum = 1:length(EEG1.chanlocs) | ||
| + | hold(ax(chanNum),'on'); | ||
| + | plot(ax(chanNum), EEG1.times, ERP1(chanNum ,:)); | ||
| + | plot(ax(chanNum), EEG2.times, ERP2(chanNum ,:)); | ||
| + | title(ax(chanNum),EEG1.chanlocs(chanNum).labels ); | ||
| + | hold(ax(chanNum),'off'); | ||
| + | end | ||
| + | </source> | ||
| + | {{hidden end}} | ||
| − | Poniżej zaprezentowany jest przykładowy skrypt do cięcia danych wokół znaczników. Działa on z plikami zawartymi w archiwum: | + | <small>Poniżej zaprezentowany jest przykładowy skrypt do cięcia danych wokół znaczników. Działa on z plikami zawartymi w archiwum: |
: [[Plik:KalibracjaP300.tar.gz]] | : [[Plik:KalibracjaP300.tar.gz]] | ||
Korzysta z funkcji pomocniczych dostępnych w dystrybucji obci w katalogu | Korzysta z funkcji pomocniczych dostępnych w dystrybucji obci w katalogu | ||
: /usr/share/openbci/analysis/matlab_obci_signal_processing | : /usr/share/openbci/analysis/matlab_obci_signal_processing | ||
| − | Openbci można pobrać z https://github.com/BrainTech/openbci | + | Openbci można pobrać z https://github.com/BrainTech/openbci</small> |
{{hidden begin|title=przykładowy skrypt}} | {{hidden begin|title=przykładowy skrypt}} | ||
| Linia 390: | Linia 421: | ||
{{hidden end}} | {{hidden end}} | ||
| − | ===Analiza CSP=== | + | ===ZADANIE: Analiza CSP=== |
| − | |||
| − | * | + | Przegląd badań o P300: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2715154/ |
| + | |||
| + | Link do Read menager [https://drive.google.com/file/d/1OgOduK5Zn7GgNl5XdCyLWXHJ7wTJIWcC/view?usp=share_link] | ||
| + | <!--- | ||
| + | [https://drive.google.com/open?id=0BzwQ_Lscn8yDS3RXNWdBbkxEQ2c] | ||
| + | ---> | ||
| + | * Wykonać analizę CSP wzmacniającą potencjał P300. | ||
* Zaprezentować średnią ze wszystkich kanałów źródłowych z warunku target (jeden kolor) i non-target (inny kolor) w subplotach ułożonych w prostokątnej siatce. Zaobserwować dla którego kanału średnie różnią się najbardziej. Czy jest związek tego kanału z wartościami własnymi? | * Zaprezentować średnią ze wszystkich kanałów źródłowych z warunku target (jeden kolor) i non-target (inny kolor) w subplotach ułożonych w prostokątnej siatce. Zaobserwować dla którego kanału średnie różnią się najbardziej. Czy jest związek tego kanału z wartościami własnymi? | ||
| Linia 399: | Linia 435: | ||
** filtrowi przestrzennemu | ** filtrowi przestrzennemu | ||
** rzutu topograficznego źródła na elektrody. | ** rzutu topograficznego źródła na elektrody. | ||
| + | <!--- | ||
| + | * Zbadać powtarzalność topografii pomiędzy plikami konfiguracyjnymi. | ||
| + | ---> | ||
| − | + | {{hidden begin|title=Wybór i separacja cech}} | |
===Wybór i separacja cech=== | ===Wybór i separacja cech=== | ||
| Linia 410: | Linia 449: | ||
** i sumujemy je w wybranym zakresie czasu. | ** i sumujemy je w wybranym zakresie czasu. | ||
* Zaobserwuj jak zmienia się separacja w grupach target i non-target. | * Zaobserwuj jak zmienia się separacja w grupach target i non-target. | ||
| + | {{hidden end}} | ||
==Filtry przestrzenne dla SSEP == | ==Filtry przestrzenne dla SSEP == | ||
| − | + | {{hidden begin|title=Filtry przestrzenne dla SSEP}} | |
=== Teoria=== | === Teoria=== | ||
Ciekawa koncepcja filtra przestrzennego dla SSVEP zaprezentowana jest tu: http://www.eurasip.org/Proceedings/Eusipco/Eusipco2009/contents/papers/1569193209.pdf | Ciekawa koncepcja filtra przestrzennego dla SSVEP zaprezentowana jest tu: http://www.eurasip.org/Proceedings/Eusipco/Eusipco2009/contents/papers/1569193209.pdf | ||
| Linia 483: | Linia 523: | ||
PP=0; | PP=0; | ||
for rep = 1:numberOfTrials | for rep = 1:numberOfTrials | ||
| − | x = signal(rep,i,:); | + | x = squeeze(signal(rep,i,:)); |
[Pxx,ff] = pwelch(x, X.sampling, 1, X.sampling, X.sampling); | [Pxx,ff] = pwelch(x, X.sampling, 1, X.sampling, X.sampling); | ||
PP =PP + Pxx; | PP =PP + Pxx; | ||
| Linia 495: | Linia 535: | ||
PP=0; | PP=0; | ||
for rep = 1:numberOfTrials | for rep = 1:numberOfTrials | ||
| − | s = S(rep,i,:); | + | s = squeeze(S(rep,i,:)); |
[Pss,ff]=pwelch(s, X.sampling, 1, X.sampling, X.sampling); | [Pss,ff]=pwelch(s, X.sampling, 1, X.sampling, X.sampling); | ||
PP =PP + Pss; | PP =PP + Pss; | ||
| Linia 506: | Linia 546: | ||
| + | ====ZADANIE: Analiza danych z eksperymentu własnego ==== | ||
| + | # Przefiltruj sygnały EEG w paśmie 1-45 Hz za pomocą procedury <tt>filtfilt</tt>. | ||
| + | # Na podstawie sygnału trigger oraz danych zapisanych w pliku wyodrębnij sygnały EEG zarejestrowane w trakcie stymulacji z odpowiednimi częstościami. | ||
| + | # Uśrednij sygnały odpowiadające stymulacji tą samą częstością. | ||
| + | # Obejrzyj uśrednione sygnały. (Zaprezentuj je). | ||
| + | |||
| + | #* Sposób I: | ||
| + | #**Dla każdej realizacji wyestymuj przy pomocy metody Welcha widmo mocy sygnału EEG. | ||
| + | #**Dla każdej częstości stymulacji wyznacz poziom tła na podstawie widm pochodzących ze stymulacji innymi częstościami. Np. dla stymulacji częstością 10 Hz poziom tła można wyznaczyć jako 95 centyl ze zbioru wartości widma w częstości 10 Hz dla stymulacji częstościami {4, 7, 13, 16, 20, 25, 30, 35, 40} Hz. | ||
| + | #**Dla każdej częstości stymulacji wyznacz miarę odpowiedzi SSVEP (amplitudę widma odpowiadającą częstości stymulacji powyżej poziomy tła dla pojedynczej próby). | ||
| + | #**Zaprezentuj widma otrzymane przy stymulacjach różnymi częstościami wraz z korytarzem odpowwiadajacym 95% przedziałowi ufności wyznaczonemu dla widm z pojedynczych realizacji. | ||
| + | #**Sporządź wykres odpowiedzi SSVEP od częstości z zaznaczeniem przedziałów ufności i poziomu tła. | ||
| + | #* Sposób II: | ||
| + | #**Wyestumuj filtr CSP-SSVEP wspólny dla wszystkich częstości stymulacji | ||
| + | #**Powtórz kroki ze sposobu I dla uzyskanych komponentów. | ||
| + | #**Zaprezentuj filtry przestrzenne i topografie dla poszczególnych komponentów | ||
| + | #**Dla przypomnienia: | ||
| + | #***Filtr to zestaw współczynników z jakimi należy zsumować sygnały z poszczególnych kanałów EEG aby dostać komponenty odpowiadające hipotetycznym źródłom nieskorelowanym. Filtr można zilustrować na głowie, przypisując poszczególnym pozycjom elektrod wagi równe współrzędnym wektora w (kolumna macierzy W). | ||
| + | #***Topografia źródła to zestaw współczynników z jakimi docierają one do poszczególnych kanałów EEG. Topografia zawarta jest w wierszach macierzy odwrotnej do W. | ||
| + | #**Można rysunki wykonać jako macierze 5x5 i w pozycji elektrody kolorujemy proporcjonalnie do współczynnika. | ||
| + | |||
| + | ===SSVEP-BCI=== | ||
| + | W zajęciach tych przydadzą nam się informacje z: | ||
| + | https://brain.fuw.edu.pl/edu/index.php/Laboratorium_EEG/Wprowadzenie_do_syg_online | ||
| + | ====Wstęp==== | ||
| + | Naszym celem będzie stworzenie prostego interfejsu wykorzystującego zjawisko SSVEP. | ||
| + | Po dwóch stronach monitora zamocujemy diody. Każda będzie migać ze swoją ustaloną częstością (np. 16 i 22 Hz) - warto zadbać aby nie były to częstości powiązane ze sobą harmonicznie, a z drugiej strony aby, biorąc pod uwagę wyniki poprzedniego zadania, dawały dobra odpowiedź SSVEP. | ||
| + | |||
| + | Eksperyment będzie miał dwie cześci: sesję kalibracje i sesję on-line. Pomiędzy tymi sesjami będziemy uczyć kalsyfikator. Na podstawie części kalibracyjnej ustalimy jakie parametry przetwarznego on-line sygnału świadczą o patrzeniu się na diodę z lewej a jakie na tą z prawej strony ekranu. | ||
| + | |||
| + | Potem w sesji online będziemy porównywać (za pomocą predykcji klasyfikatora) rejestrowany sygnał z tymi warościami kalibracyjnymi i na tej podstawie system będzie zwracał informację o wyborze lewej lub prawej diody. To powinno umożliwić prostą komunikację na zasadzie pytanie i odpowiedź TAK/NIE. | ||
| + | |||
| + | ==== Sesja kalibracycjna==== | ||
| + | * Zakładamy czepek | ||
| + | * Częstość próbkowania ustawiamy na 256Hz | ||
| + | * Na podstawie kodu: https://brain.fuw.edu.pl/edu/index.php/Laboratorium_EEG/Wprowadzenie_do_syg_online#.C4.86wiczenie:_Wykorzystanie_pomiaru_EMG_do_sterowania_on-line | ||
| + | tworzymy programik, który zamiast pętli while tworzy odpowiednie pętle for aby: | ||
| + | * pięciokrotnie zarejestrować sekwencję trzech warunków eksperymentalnych: | ||
| + | ** patrz 5s na diodę z lewej (warunek l) | ||
| + | ** patrz 5s na środek ekranu (warunek s) | ||
| + | ** patrz 5s na diodę z prawej (warunek p) | ||
| + | * w czasie tego patrzenia: | ||
| + | ** odbieramy próbki w pakietach o długości 0.5s | ||
| + | ** każdy pakiet filtrujem (technika filtrowania on-line) w pasmach dookoła wybranych dwóch częstości (PASMO_LEWE / PASMO_PRAWE) | ||
| + | ** przefiltrowany pakiet przeliczamy na RMS | ||
| + | ** zbieramy sześć zbiorów wyników - zestawy RMSów związane z każdym z waunków kalibracyjnych (LEWY/SPOCZYNEK/PRAWY) dla PASMO_LEWE i PASMO_PRAWE. | ||
| + | * Normalizujemy RMSy. Dla pasma lewego obliczamy (RMS_(l/p/s) - np.mean(RMS_s)) / np.sdt(RMS_s) i analogicznie dla pasma prawego. Małe indeksy oznaczaają tu warunki. Zapamiętujemy współczynniki normalizacyjne. | ||
| + | ** Ogladamy rozkłady uzyskanych wielkości (znormalizowanych RMSów). | ||
| + | ** Uczymy klasyfikator np. regresję logistyczną (https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegression.html) do rozpoznawania, z którym warunkiem patrzenia mamy do czynienia. | ||
| + | |||
| + | ==== Sesja online==== | ||
| + | * wczytujemy wyuczony model i kalibracyjne wartości np.mean(RMS_s)) i np.sdt(RMS_s) dla pasm lewego i prawego | ||
| + | * Odbieramy próbki w pakietach o długości 0.5s | ||
| + | ** każdy pakiet filtrujem (technika filtrowania on-line) w pasmach dookoła wybranych dwóch częstości (PASMO_LEWE / PASMO_PRAWE) | ||
| + | ** przefiltrowany pakiet przeliczamy na RMS | ||
| + | ** Normalizujemy RMSy. Dla pasma lewego obliczamy (RMS_(l/p/s) - np.mean(RMS_s)) / np.sdt(RMS_s) i analogicznie dla pasma prawego. Małe indeksy oznaczaają tu warunki. | ||
| + | ** robimy predykcję klasyfikatora, z którym warunkiem patrzenia mamy do czynienia. Wyświetlamy na ekranie komunikat. | ||
| + | * Testujemy czy powyższy schemat analizy pozwala na komunikację. | ||
| + | {{hidden end}} | ||
<!-- | <!-- | ||
===Eksperyment ASSR=== | ===Eksperyment ASSR=== | ||
| Linia 543: | Linia 642: | ||
==ICA jako filtr przestrzenny== | ==ICA jako filtr przestrzenny== | ||
| + | {{hidden begin|title=Wstęp teoretyczny do ICA}} | ||
===Definicja === | ===Definicja === | ||
Independent Component Analysis (ICA) jest metodą statystycznej analizy sygnałów, która dokonuje dekompozycji wielokanałowych zapisów na składowe niezależne w sensie statystycznym. | Independent Component Analysis (ICA) jest metodą statystycznej analizy sygnałów, która dokonuje dekompozycji wielokanałowych zapisów na składowe niezależne w sensie statystycznym. | ||
| Linia 595: | Linia 695: | ||
===Obliczenia=== | ===Obliczenia=== | ||
| − | Intuicyjna heurystyka poszukiwania najbardziej niegaussowskich składowych może być użyta do wyprowadzenia różnych funkcji kosztu, których optymalizacja daje model ICA, np. kurtoza. Procedura wykorzystywana w eeglabie („runica”, Makeig 1996) dąży do minimalizacji informacji wzajemnej. Oba podejścia są w przybliżeniu równoważne (Hyvärinen, 2000), chociaż owo przybliżenie dla sygnałów elektrofizjologicznych nie zostało to jeszcze w pełni wyeksplorowane. | + | Intuicyjna heurystyka poszukiwania najbardziej niegaussowskich składowych może być użyta do wyprowadzenia różnych funkcji kosztu, których optymalizacja daje model ICA, np. kurtoza. |
| + | |||
| + | <math>kurt(y) = E\{y^4\} - 3(E{y^2})^2</math> | ||
| + | |||
| + | Inną miarą gassowskości jest neg-entropia, którą można wyprowadzić z entropii: | ||
| + | Entropia jest miarą średniego zdziwienia wynikiem obserwacji zmiennej losowej: | ||
| + | <math>H(Y) = - \sum_i P(Y= a_i) \log(P(Y=a_i)) </math> | ||
| + | |||
| + | Negentropia jest zdefiniowana: | ||
| + | |||
| + | <math> J(y) = H(y_{gauss}) -H(y)</math> | ||
| + | gdzie <math> y_{gauss} </math> jest gassuwską zmienną losową o takiej samej kowaiancji jak <math> y </math>. | ||
| + | |||
| + | Negentropia jest skomplikowana obliczeniow, więc w praktyce używana jest formuła przybliżona: | ||
| + | |||
| + | <math> J(y) \varpropto [E\{G (y)\} - E\{G(\nu)\}]</math> | ||
| + | |||
| + | <math>\nu </math> jest zmienną losową ze standardowego rozkładu normalnego , a G są pewnymi niekwadratowymi funkcjami. | ||
| + | |||
| + | W algorytmie FastICA extremum negentropii jest znajdowane w procedurze bazującej na optymalizacji Netwona. | ||
| + | (szczegóły np.: sekcja 6 w https://www.cs.helsinki.fi/u/ahyvarin/papers/NN00new.pdf) | ||
| + | |||
| + | |||
| + | Procedura wykorzystywana w eeglabie („runica”, Makeig 1996) dąży do minimalizacji informacji wzajemnej. Oba podejścia są w przybliżeniu równoważne (Hyvärinen, 2000), chociaż owo przybliżenie dla sygnałów elektrofizjologicznych nie zostało to jeszcze w pełni wyeksplorowane. | ||
Dla sygnałów o niskiej wymiarowości i spełniających dokładnie założenia ICA wszystkie powszechnie wykorzystywane algorytmy dają niemal identyczne wyniki. | Dla sygnałów o niskiej wymiarowości i spełniających dokładnie założenia ICA wszystkie powszechnie wykorzystywane algorytmy dają niemal identyczne wyniki. | ||
| Linia 608: | Linia 731: | ||
===Bibliografia=== | ===Bibliografia=== | ||
| + | Bazowa praca: | ||
| + | * A. Hyvärinen. Fast and Robust Fixed-Point Algorithms for Independent Component Analysis. IEEE Transactions on Neural Networks 10(3):626-634, 1999 http://www.cs.helsinki.fi/u/ahyvarin/papers/TNN99_reprint.pdf | ||
| + | |||
| + | Nieco prościej opisana wersja z przykładami: | ||
| + | * Hyvärinen, A. and Oja, E. (2000). Independent component analysis: Algorithms and applications. Neural Networks, 13(4-5):411–430. | ||
| + | https://www.cs.helsinki.fi/u/ahyvarin/papers/NN00new.pdf | ||
| + | |||
* Grau, C., Fuentemilla, L., Marco-Pallars, J. (2007). Functional neural dynamics underlying auditory event-related n1 and n1 suppression response. Neuroimage, 36(6):522–31. | * Grau, C., Fuentemilla, L., Marco-Pallars, J. (2007). Functional neural dynamics underlying auditory event-related n1 and n1 suppression response. Neuroimage, 36(6):522–31. | ||
| − | |||
* Makeig, S., Bell, A., Jung, T.-P., Sejnowski,T. (1996). Independent component analysis of electroencephalographic data. W: Touretzky, D., Mozer, M., and Hasselmo, M., editors, Advances in Neural Information Processing Systems, volume 8, pages 145–151. MIT Press, Cambridge, MA. | * Makeig, S., Bell, A., Jung, T.-P., Sejnowski,T. (1996). Independent component analysis of electroencephalographic data. W: Touretzky, D., Mozer, M., and Hasselmo, M., editors, Advances in Neural Information Processing Systems, volume 8, pages 145–151. MIT Press, Cambridge, MA. | ||
* Onton, J., Makeig, S. (2006). Information-based modeling of event-related brain dynamics. Prog Brain Res., 159:99–120. | * Onton, J., Makeig, S. (2006). Information-based modeling of event-related brain dynamics. Prog Brain Res., 159:99–120. | ||
| Linia 615: | Linia 744: | ||
* http://sccn.ucsd.edu/~arno/indexica.html | * http://sccn.ucsd.edu/~arno/indexica.html | ||
* http://cis.legacy.ics.tkk.fi/aapo/papers/IJCNN99_tutorialweb/ | * http://cis.legacy.ics.tkk.fi/aapo/papers/IJCNN99_tutorialweb/ | ||
| + | {{hidden end}} | ||
| + | {{hidden begin|title=Wydobywanie interesujących komponentów}} | ||
| − | === Wydobywanie interesujących komponentów === | + | === ZADANIE: Wydobywanie interesujących komponentów === |
Dane do tej części ćwiczeń proszę pobrać i rozpakować w swoim katalogu: | Dane do tej części ćwiczeń proszę pobrać i rozpakować w swoim katalogu: | ||
| Linia 639: | Linia 770: | ||
** Czy uzyskiwane komponenty są powtarzalne? | ** Czy uzyskiwane komponenty są powtarzalne? | ||
** Swoje wyniki porównać też z sąsiednimi grupami. | ** Swoje wyniki porównać też z sąsiednimi grupami. | ||
| + | {{hidden end}} | ||
| − | === Identyfikacja artefaktów === | + | ===ZADANIE: Identyfikacja artefaktów === |
Proszę pobrać dane: | Proszę pobrać dane: | ||
| Linia 656: | Linia 788: | ||
* obejrzyj topografię komponentów | * obejrzyj topografię komponentów | ||
* zidentyfikuj komponenty odpowiadające mruganiu i aktywności mięśniowej. | * zidentyfikuj komponenty odpowiadające mruganiu i aktywności mięśniowej. | ||
| + | ;UWAGA: Aktualnie do wykrywania komponentów artefaktowych warto posłużyć się wtyczkami do eeglaba dostępnymi przez stronę: | ||
| + | |||
| + | https://sccn.ucsd.edu/eeglab/plugin_uploader/plugin_list_all.php | ||
| + | |||
| + | * ICLabel | ||
| + | * MARA | ||
| + | |||
| + | ====W raporcie: ==== | ||
| + | * zaprezentuj fragmenty sygnału zawierającego artefakty oczne i mięśniowe przed i po zastosowaniu czyszczenia poprzez usuwanie komponentów zdominowanych przez artefakty. | ||
| + | * zaprezentuj topografię i przebiegi czasowe komponentów zidentyfikowanych jako artefakty oczne i mięśniowe. | ||
| + | |||
| + | |||
<!-- | <!-- | ||
| Linia 663: | Linia 807: | ||
--> | --> | ||
| + | <!--- | ||
==Eksperyment ASSR== | ==Eksperyment ASSR== | ||
W eksprymencie wykorzystujemy układ do generacji potencjałów słuchowych stanu ustalonego (ASSR). Wejście układu ASSR typu mini-jack wkładamy w wyjście słuchawkowe w laptopie. Drugie wejście układu ASSR wkładamy do wyjścia triggera we wzmacniaczu. Uruchamiamy plik dźwiękowy MM40tr.wav. Można go znalezc w: http://www.fuw.edu.pl/~suffa/LabEEG/MM40tr.wav | W eksprymencie wykorzystujemy układ do generacji potencjałów słuchowych stanu ustalonego (ASSR). Wejście układu ASSR typu mini-jack wkładamy w wyjście słuchawkowe w laptopie. Drugie wejście układu ASSR wkładamy do wyjścia triggera we wzmacniaczu. Uruchamiamy plik dźwiękowy MM40tr.wav. Można go znalezc w: http://www.fuw.edu.pl/~suffa/LabEEG/MM40tr.wav | ||
| Linia 694: | Linia 839: | ||
Transformacja Hjortha jest przybliżeniem numerycznym transformacji Laplace'a, czyli drugiej pochodnej przestrzennej. Obliczamy ją jako różnicę potencjału pomiędzy daną elektrodą i średnią z czterech sąsiednich elektrod. | Transformacja Hjortha jest przybliżeniem numerycznym transformacji Laplace'a, czyli drugiej pochodnej przestrzennej. Obliczamy ją jako różnicę potencjału pomiędzy daną elektrodą i średnią z czterech sąsiednich elektrod. | ||
Przelicz potencjały z elektrod, w których występuję odpowiedź ASSR na montaż Hjortha i powtórz analizę opisaną powyżej. | Przelicz potencjały z elektrod, w których występuję odpowiedź ASSR na montaż Hjortha i powtórz analizę opisaną powyżej. | ||
| + | ---> | ||
Wersja z 08:47, 14 maj 2024
Laboratorium_EEG/BSS
Spis treści
Prezentacja
Ślepa separacja źródeł (BSS)
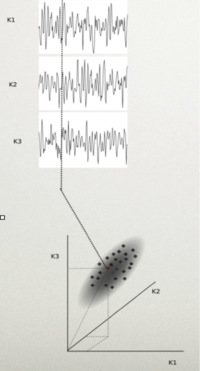
Rozważmy N-kanałowy sygnał EEG. Próbkę tego sygnału możemy przedstawić jako punkt w przestrzeni rozpiętej przez osie, z których każda reprezentuje wartość potencjału w jednym kanale. Cały sygnał tworzy w tej przestrzeni chmurę punktów. Rozciągłość tej chmury w danym kierunku mówi nam o wariancji (zmienności) sygnału w tym kierunku.
Taki zbiór punktów wygodniej jest analizować w układzie współrzędnych zgodnym z osiami głównymi macierzy kowariancji. W dalszej części rozważań założymy, że te przestrzenie, w których rozważamy sygnały są przestrzeniami wektorowymi, a pojedyncze próbki wielokanałowego sygnału są wektorami.
Filtry przestrzenne i ślepa separacja źródeł
Sygnał EEG jest superpozycją aktywności elektrycznej wielu źródeł. Jak można estymować aktywność samych źródeł?
Niech:
- [math]s(t)[/math] - aktywność niezależnych źródeł,
- [math]x(t)[/math] mierzony sygnał
- [math]A[/math] macierz przejścia taka, że:
- [math]x(t) = A s(t)[/math] (*)
- [math]s(t) = A^{-1}x(t) = P x(t)[/math]
Macierz kowariancji dla sygnałów [math]x(t)[/math] estymujemy tak:
- [math] C_x = E[x(t)x(t)^T][/math]
Podstawiając (*) mamy:
- [math] C_x = E[x x^T] = E[As(As)^T] = A E[s s^T] A^T = A C_s A^T[/math]
Z założenia, że źródła są niezależne wynika, że macierz [math]C_s[/math] jest diagonalna. Przekształcając powyższe równanie możemy zapisać:
- [math]A^{-1} C_x (A^T)^{-1} = P C_x P^T = C_s[/math]
Odwzorowanie [math]P = A^{-1}[/math] diagonalizuje macierz [math]C_x[/math].
Powyższe rozumowanie jest słuszne w przypadku gdy mamy do czynienia z sygnałem stacjonarnym, tzn. jego macierz kowariancji jest niezależna od czasu, czyli przez cały czas aktywna jest ta sama konfiguracja źródeł niezależnych. W przypadku gdy tak nie jest to konstrukcję filtra przestrzennego można oprzeć o jednoczesną diagonalizację macierzy kowariancji odpowiadających różnym stanom osoby badanej.
Common Spatial Pattern
Koncepcja
Dla ustalenia uwagi możemy myśleć o eksperymencie wywołującym potencjał P300. Mamy w nim dwie sytuacje eksperymentalne. Oznaczmy [math]T[/math] (target) próby, w których pojawił się oczekiwany bodziec, zaś [math]NT[/math] (non-target) gdy pojawił się bodziec standardowy. Chcielibyśmy znaleźć taki montaż (czyli taką kombinację liniową kanałów), który maksymalizuje stosunek mocy (wariancji) sygnałów rejestrowanych w dwóch rożnych warunkach eksperymentalnych.
Formalizm
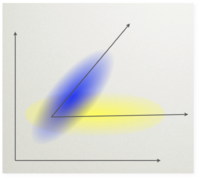
Metoda ta polega na znalezieniu takiego kierunku [math]w[/math] w przestrzeni sygnałów, że sygnał z warunku [math]T[/math] rzutowany na ten kierunek ma dużą wariancje a sygnał z warunku [math]NT[/math] ma wariancję małą.
Rzutowanie sygnału [math]x(t)[/math] na kierunek [math]w[/math] odbywa się przez policzenie iloczynu skalarnego dla każdej chwili czasu [math]t[/math]:
- [math] s_w(t) = w^T x(t)[/math]
Wariancja tego rzutowanego sygnału to:
- [math] \mathrm{var}(s_w) = E[s_w s_w^T] = E[ w^T x (w^T x)^T] = w^T E[x x^T] w = w^T C_x w [/math]
Zatem znalezienie właściwego kierunku rzutowania można wyrazić jako szukanie maksimum wyrażenia [math] J(w) [/math] (jest to tzw. iloraz Rayleigha):
- [math]J(w) = \frac{w^T C_T w}{w^T C_{NT} w} [/math]
Ekstremum tego ilorazu można znaleźć poprzez policzenie gradientu [math]J(w)[/math] i przyrównanie go do zera:
- [math] \nabla J(w) = \frac{ 2 C_{T} w \left(w^T C_{NT} w\right) -2C_{NT} w \left(w^T C_{T} w \right)}{\left(w^T C_{NT} w\right)^2} = \frac{ 2}{w^T C_{NT} w}\left[ C_{T}w -\frac{w^T C_{T} w}{w^T C_{NT} w} C_{NT} w \right][/math]
Przyrównując to wyrażenie do zera dostajemy do rozwiązania tzw. uogólnione zagadnienie własne:
- [math] C_{T}w =\frac{w^T C_{T} w}{w^T C_{NT} w} C_{NT} w [/math]
We wzorze tym liczba [math]\lambda=\frac{w^T C_{T} w}{w^T C_{NT} w}[/math] spełniająca to równanie jest uogólnioną wartością własną, wtedy [math]w[/math] jest uogólnionym wektorem własnym odpowiadającym tej wartości.
Aby znaleźć [math] \lambda[/math] i [math]w[/math] możemy wykorzystać w Matlabie funkcję eig. Funkcja ta rozwiązuje (również) uogólnione zagadnienia własne postaci Aw=λBw dostarczając w wyniku macierz wektorów własnych (w kolumnach) oraz macierz zawierającą na przekątnej odpowiadające im wartości własne.
Ćwiczenie symulacyjne
% symulowany eksperyment składa się z sinusoidy udającej alfę spoczynkową i
% funkcji Gaussa udającego potencjał wywołany
% źródła te są symulowane niezależnie a potem mieszane przez macierz A
% symulujemy źródła
% s1 - symuluje alfę
% s2 - symuluje "potencjał wywołany" (ERP)
%ustawiamy parametry do symulacji sygnałów
Fs = 100;
T = 1;
t = 0:1/Fs:T-1/Fs;
N_rep = 100;
N_chan = 2;
s = zeros(N_rep,N_chan, length(t));
X = zeros(N_rep,N_chan, length(t));
% filtr przestrzenny - z takimi wagami trzeba wziąść kanały EEG aby odzyskać sygnały źródłowe
P = [1 2
1.5 1.3];
% topografie - z takimi wagami źródła dokładają się do poszczególnych elektrod
A = P^(-1);
for r =1:N_rep % tworzymy kolejne realizacje "eksperymentu"
s1 = sin(2*pi*11*t +pi/2+ 0*2*pi*rand())+ 0.02*randn(size(t)); % źródło alfa
s2 = exp(-((t-0.8)/0.05).^2)+ 0.01*randn(size(t)); % źródło ERP
s(r,1,:) = s1;
s(r,2,:) = s2;
tmp = squeeze(s(r,:,:));
n = 0*randn(size(tmp));
X(r,:,:) = A*tmp +n; % rzutujemy sygnały źródłowe na elektrody s -> x
end
% wycinamy warunki
% baseline_ind to indeksy pierwszej połowy każdego powtórzenia "baseline"
% ERP_ind to indeksy drugiej połowy każdego powtórzenia zawierająca "ERP"
baseline_ind = find(t<0.5);
ERP_ind = find(t>=0.5);
x_baseline_kan_1 = X(:,1,baseline_ind);
x_baseline_kan_2 = X(:,2,baseline_ind);
x_ERP_kan_1 = X(:,1,ERP_ind);
x_ERP_kan_2 = X(:,2,ERP_ind);
% liczymy średnie macierze kowariancji:
R_E = zeros(N_chan,N_chan);
R_B = zeros(N_chan,N_chan);
for r =1:N_rep
B = squeeze(X(r,:,baseline_ind));
tmp =cov(B');
R_B = R_B + tmp./trace(tmp);%B*B' ;
E = squeeze(X(r,:,ERP_ind));
tmp = cov(E');
R_E = R_E + tmp./trace(tmp);%E*E' ;
end
R_B = R_B/N_rep;
R_E = R_E/N_rep;
% rozwiązujemy uogólnione zagadnienie własne
[W,Lambda]=eig(R_E,R_B); % możliwa jest też optymalizacja wzg. średniej macierzy kowariancji (R_B+R_A)/2);
% odzyskujemy sygnały źródeł
for r =1:N_rep
S(r,:,:) = W'*squeeze(X(r,:,:));
end
% pobieramy wycinki odpowiadające obu częściom eksperymentu z estymowanych
% źródeł
s_baseline_estymowany_kan1 = squeeze( S(:,1,baseline_ind));
s_baseline_estymowany_kan2 = squeeze( S(:,2,baseline_ind));
s_ERP_estymowany_kan1 = squeeze(S(:,1,ERP_ind));
s_ERP_estymowany_kan2 = squeeze(S(:,2,ERP_ind));
%%%%%%%%%%%%%% Ilustracje %%%%%%%%%%%%%%%%%%%%%%%
% ilustracja sygnałów mierzonych
figure(1);clf
subplot(2,2,1);
plot(t(baseline_ind),(squeeze(X(:,1,baseline_ind)))','b'); hold on
plot(t(ERP_ind),(squeeze( X(:,1,ERP_ind)))','r'); hold off
xlabel('elektroda 1')
title('ilustracja sytuacji pomiarowej -\newline znane są potencjały na elektrodach w dwóch warunkach eksperymentalnych')
subplot(2,2,3);
plot(t(baseline_ind),(squeeze(X(:,2,baseline_ind)))','b'); hold on
plot(t(ERP_ind),(squeeze( X(:,2,ERP_ind)))','r'); hold off
xlabel('elektroda 2')
subplot(1,2,2)
plot(x_baseline_kan_1(:),x_baseline_kan_2(:),'b.');
hold on
plot(x_ERP_kan_1(:),x_ERP_kan_2(:),'r.');
xlim([-2,2])
ylim([-2,2])
axis equal
% wektor własny odpowiadający największej wartości własnej jest
% kierunkiem najbardziej różnicującym warunki eksperymentalne
disp('wartości własne znajdują się na przekątnej macierzy Lambda')
disp(Lambda)
% rysujemy wersory jednostkowe w kierunkach wektorów własnych
w1 = W(:,1);
w1 = w1/norm(w1);
w2 = W(:,2);
w2 = w2/norm(w2);
line([0, w1(1) ],[0,w1(2)],'Color',[0,0.3,0])
text(w1(1),w1(2),'wektor własny 1')
line([0, w2(1) ],[0,w2(2)],'Color',[1,0,1])
text(w2(1),w2(2),'wektor własny 2')
xlabel('Amplituda na elektrodzie 1')
ylabel('Amplituda na elektrodzie 2')
legend('baseline','ERP')
% Ilustracja estymowanych źródeł
figure(2);clf
subplot(2,2,1);
plot(t(baseline_ind),(squeeze(S(:,1,baseline_ind)))','b');hold on
plot(t(ERP_ind),(squeeze(S(:,1,ERP_ind)))','r');hold off
xlabel('estymowane zrodlo 1')
title('ilustracja estymacji -\newline estymowane są potencjały źródeł w dwóch warunkach eksperymentalnych')
subplot(2,2,3);
plot(t(baseline_ind),(squeeze(S(:,2,baseline_ind)))','b');hold on
plot(t(ERP_ind),(squeeze(S(:,2,ERP_ind)))','r');hold off
xlabel('estymowane zrodlo 2');
subplot(1,2,2)
plot(s_baseline_estymowany_kan1(:),s_baseline_estymowany_kan2(:),'b.');
hold on
plot(s_ERP_estymowany_kan1(:),s_ERP_estymowany_kan2(:),'r.');
xlabel('Amplituda estym. źródła 1')
ylabel('Amplituda estym. źródła 2')
legend('baseline','ERP')
Zastosowanie filtra CSP do detekcji potencjału P300
Eksperyment
- Proszę zapoznać się z instrukcją: http://laboratorium-eeg.braintech.pl/rozdz10.html
- Proszę wczytać i uruchomić (na sucho) demo Demos->EEG_P300wz
- Wspólne omówienie konstrukcji i potencjalnych modyfikacji tego scenariusza
Przygotowanie do badania:
- założyć czepek z elektrodami w systemie 10-20;
- elektrody referencyjne: M1 i M2;
- elektroda GND w pozycji AFz.
Analiza wstępna
Poszczególne etapy analizy proszę kodować w osobnych funkcjach. Funkcje te powinny być wywoływane z nadrzędnego skryptu, który powinien umożliwic wykoanie całości analiz.
- Wczytać dane kalibracyjne do Matlaba i pociąć je na realizacje typu T — „target” (związane z wystąpieniami litery „B”) i NT — „non-target” (pozostałe litery) o długości −200 do +800 ms wokół triggerów. Dla każdej realizacji odjąć trend liniowy.
- Sygnał zmontować wzgl. „połączonych uszu” i wyświetlić średnie przebiegi dla warunku T i NT w układzie topograficznym — można wykorzystać w tym celu poniższy fragment kodu.
%% stworzenie osi
% zakładam, że dane do rysowania są w dwóch strukturach EEG1 i EEG2 (struktury eeglab),
% te dane są podzielone na realizacje i mają kształt (kanały , czas, epoki)
% i że mamy już załadowane położenia elektrod we współrzędnych
% biegunowych
w = 0.125;
h = 0.125;
sc = 0.8;
figure()
for chanNum = 1:length(EEG1.chanlocs)
r =EEG1.chanlocs(chanNum).radius;
theta = EEG1.chanlocs(chanNum).theta;
x = r* sin(theta/180*pi)*sc+0.46;
y = r* cos(theta/180*pi)*sc+0.46;
ax(chanNum) = axes('Position', [x, y, w, h]);
end
%%uśredniam EEG po powtórzeniach aby otrzymać ERP
ERP1 =squeeze( mean( EEG1.data,3)) ;
ERP2 =squeeze( mean( EEG2.data,3)) ;
%% rysowanie uśrednionych potencjałów z dwóch struktur EEG
for chanNum = 1:length(EEG1.chanlocs)
hold(ax(chanNum),'on');
plot(ax(chanNum), EEG1.times, ERP1(chanNum ,:));
plot(ax(chanNum), EEG2.times, ERP2(chanNum ,:));
title(ax(chanNum),EEG1.chanlocs(chanNum).labels );
hold(ax(chanNum),'off');
end
Poniżej zaprezentowany jest przykładowy skrypt do cięcia danych wokół znaczników. Działa on z plikami zawartymi w archiwum:
Korzysta z funkcji pomocniczych dostępnych w dystrybucji obci w katalogu
- /usr/share/openbci/analysis/matlab_obci_signal_processing
Openbci można pobrać z https://github.com/BrainTech/openbci
% ustalamy nzawy plików z danymi
nazwaPliku = 'p_6301423_calibration_p300.obci';
nameOfXMLFile = strcat(nazwaPliku,'.xml');
nameOfTagFile = strcat(nazwaPliku,'.tag'); %tagi = znaczniki zdarzeń
namesOfDataFiles = strcat(nazwaPliku,'.raw');
% inicjujemy obiekt rm
rm = ReadManager(nameOfXMLFile,namesOfDataFiles,nameOfTagFile);
% obieramy przydatne parametry i znaczniki
numberOfChannels = rm.get_param('number_of_channels');
namesOfChannels = rm.get_param('channels_names');
samplingFrequency = rm.get_param('sampling_frequency');
tagsStruct = rm.get_tags();
% tworzenie list znaczników Target i NonTarget
numberOfStruct = length(tagsStruct);
targetTimeStamps = [];
NonTargetTimeStamps = [];
for structNumber = 1:numberOfStruct % iterujemy się przez tagi
if(strcmp(tagsStruct(structNumber).name,'blink')) % szukamy tagów o nazwie 'blink'
index = tagsStruct(structNumber).children.index; % tu jest numer pola stymulacji
target= tagsStruct(structNumber).children.target;% tu jest numer pola na którym wyświetlany jest target
if index == target % warunek na to, że mamy do czynienia z tagiem target
targetTimeStamps = [targetTimeStamps tagsStruct(structNumber).start_timestamp]; %dodajemy timeStamp do listy targetów
else
NonTargetTimeStamps = [NonTargetTimeStamps tagsStruct(structNumber).start_timestamp];%dodajemy timeStamp do listy non-targetów
end
end
end
% pobieramy próbki
samples = double(rm.get_samples()); % konwersja na double jest potrzebna żeby dobrze funkcjonowało filtrowanie
samples=samples(1:8,:); % odrzucamy kanały, które nie mają EEG
numberOfChannels =8;
% filtrujemy dolnoprzepustowo aby odrzucić artefakty sieci i część
% artefaktów mięśniowych
[b,a] = cheby2(6,80,25 /(samplingFrequency/2),'low');
for ch = 1:numberOfChannels
samples(ch,:)=filtfilt(b,a,samples(ch,:));
end
% montujemy dane do wspólnej średniej (common average)
M = -ones(8,8)/8;
M=M+eye(8,8)*9/8;
samples = 0.0715*M*samples;
% wycinamy dane wokół znaczników
PRE = -0.2; % czas przed tagiem w sek.
POST = 0.8; % czas po tagu w sek.
wycinek = floor(PRE*samplingFrequency:POST*samplingFrequency); % tablica ze "standardowymi" indeksami do cięcia
% pobieramy targety
TargetSignal = zeros(length(targetTimeStamps),numberOfChannels, length(wycinek)); % tablica na sygnały target
for trialNumber = 1:length(targetTimeStamps)
trigerOnset = floor(targetTimeStamps(trialNumber)*samplingFrequency);
tenWycinek = wycinek + trigerOnset;
if tenWycinek(1)>0 && tenWycinek(end)<=size(samples,2) % test czy wycinek który chcemy pobrać nie wystaje poza dostępny sygnał
tmpSignal = samples(:,tenWycinek);
tmpSignal = detrend(tmpSignal')'; % usuwanie liniowego trendu - przy krótkich wycinkach działa lepiej niż filtrowanie górnoprzepustowe
TargetSignal(trialNumber, :,:) = tmpSignal;
end
end
% pobieramy non-targety
NonTargetSignal = zeros(length(NonTargetTimeStamps),numberOfChannels, length(wycinek));% tablica na sygnały non-target
for trialNumber = 1:length(NonTargetTimeStamps)
trigerOnset = floor(NonTargetTimeStamps(trialNumber)*samplingFrequency);
tenWycinek = wycinek + trigerOnset;
if tenWycinek(1)>0 && tenWycinek(end)<=size(samples,2)
tmpSignal = samples(:,tenWycinek);
tmpSignal = detrend(tmpSignal')';
NonTargetSignal(trialNumber, :,:) = tmpSignal;
end
end
%
% dla ilustracji podglądamy średnie po powtórzeniach ze wszystkich targetów
% i non-targetów
plot(squeeze(mean(TargetSignal,1))','r');
hold on
plot(squeeze(mean(NonTargetSignal,1))','b')
ZADANIE: Analiza CSP
Przegląd badań o P300: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2715154/
Link do Read menager [1]
- Wykonać analizę CSP wzmacniającą potencjał P300.
- Zaprezentować średnią ze wszystkich kanałów źródłowych z warunku target (jeden kolor) i non-target (inny kolor) w subplotach ułożonych w prostokątnej siatce. Zaobserwować dla którego kanału średnie różnią się najbardziej. Czy jest związek tego kanału z wartościami własnymi?
- Dla kanału najbardziej różnicującego wykonać mapki topograficzne (do wykonania tych mapek wykorzystać funkcję topoplot z pakietu eeglab) wektorów odpowiadających:
- filtrowi przestrzennemu
- rzutu topograficznego źródła na elektrody.
Wybór i separacja cech
- Przedstaw na rysunkach nałożone na siebie pojedyncze realizacje z warunków target i non-target po rzutowaniu na wektor [math]w[/math] odpowiadający największej i kolejnej wartości własnej.
- Przedstaw wykresy punktowe takie, że na jednej osi jest moc sygnału (suma kwadratów wartości próbek w wybranym zakresie czasu) odpowiadającego największej wartości własnej, a na drugiej osi kolejnej (mniejszej) wartości własnej; jeden punkt reprezentuje jedno powtórzenie.
- Wykonaj serię wykresów jak w poprzednim punkcie dla uśrednień sygnałów kolejno po 2, 4, 6, 8 i 10 realizacjach:
- Liczymy potencjał wywołany dla danej liczby powtórzeń.
- Następnie podnosimy wartości próbek do kwadratu
- i sumujemy je w wybranym zakresie czasu.
- Zaobserwuj jak zmienia się separacja w grupach target i non-target.
Filtry przestrzenne dla SSEP
Teoria
Ciekawa koncepcja filtra przestrzennego dla SSVEP zaprezentowana jest tu: http://www.eurasip.org/Proceedings/Eusipco/Eusipco2009/contents/papers/1569193209.pdf
Pokrótce można ją rozumieć podobnie do tego co robiliśmy rozważając filtry przestrzenne CSP z tym, że dla SSVEP oraz innych potencjałów wywołanych stanu ustalonego możemy skorzystać z dodatkowych informacji dotyczących poszukiwanych źródeł. Wiemy mianowicie, że powinny one oscylować z częstością bodźca, i być może jej harmonicznych.
Przyda nam się macierz [math]S[/math] zbudowana tak, że w kolejnych kolumnach znajdują się sinusy i cosinusy kolejnych częstości harmonicznych. Wektory te unormujemy, żeby miały energię równą 1. Innymi słowy macierz [math]S[/math] zbudowana jest z wersorów rozpinających przestrzeń, w której powinien znajdować się sygnał SSVEP.
W matlabie możemy taką macierz zbudować tak:
% Fs - częstość próbkowania
% numberOfSamples - długość sygnału w próbkach
% numberOfHarmonics - liczba harmonicznych, które chcemy włączyć do analizy
t = (0:1:numberOfSamples - 1)/Fs;
S = zeros(numberOfSamples, 2*numberOfHarmonics);
for harmonicNumber = 1:numberOfHarmonics
c = cos(2*pi*stimulationFrequency*harmonicNumber*t);
s = sin(2*pi*stimulationFrequency*harmonicNumber*t);
S(:,(harmonicNumber - 1)*2 + 1) = c/norm(c);
S(:,(harmonicNumber - 1)*2 + 2) = s/norm(s);
end
Aby w badanym sygnale znaleźć składowe odpowiadające SSVEP musimy rzutować sygnał [math]X[/math] (macierz sygnałów kanały × próbki) na przestrzeń rozpiętą przez [math]S[/math]:
- [math]A = X*S[/math]
Macierz [math]A[/math] zawiera współczynniki będące iloczynami skalarnymi sygnałów i wersorów. Mówią one o tym „jak dużo” jest sinusa bądź cosinusa o danej częstości w pierwotnym sygnale. Komponenty SSVEP zawarte w sygnale [math]X[/math] odzyskujemy tak:
- [math]\mathrm{SSVEP} = A S^T[/math]
Modelujemy rejestrowany sygnał jako:
- [math]X = \mathrm{SSVEP} + Y [/math]
gdzie:
- [math]Y = X-\mathrm{SSVEP}[/math]
- to wszystkie komponenty sygnału, które nas nie interesują.
Filtr przestrzenny, który chcemy zbudować powinien maksymalizować stosunek wariancji [math]\mathrm{SSVEP} = A S^T[/math] do wariancji [math]Y = X-\mathrm{SSVEP}[/math]. Macierz kowariancji powinna być uśredniona po powtórzeniach a kowariancja sygnału w każdym powtórzeniu powinna być znormalizowana poprzez podzielenie przez jej ślad (Matlabowa funkcja cov już wykonuje tę operację). Dalej możemy zastosować technikę znaną z konstrukcji filtrów CSP, tzn. maksymalizacji ilorazu Rayleigha za pomocą rozwiązania uogólnionego zagadnienia własnego dla macierzy kowariancji [math]\mathrm{SSVEP} [/math] i [math]Y [/math].
Poniżej prosta demonstracja dla danych zebranych EEG przy stymulacji SSVEP z częstotliwością 38 Hz.
Spakowane dane: Plik:PrzykladoweDaneSSVEP.mat.gz.
W oparciu o powyższy opis proszę zaimplementować funkcję cosSinCSP. Prawidłowo zaimplementowana funkcja wraz z poniższym kodem powinna generować rysunek:
 Przykładowy skrypt i dane prezentujący konstrukcję i działanie tego typu filtrów przestrzennych dla pełnych danych z eksperymentu SSVEP: Plik:SSVEP demo csp.tar.gz
Przykładowy skrypt i dane prezentujący konstrukcję i działanie tego typu filtrów przestrzennych dla pełnych danych z eksperymentu SSVEP: Plik:SSVEP demo csp.tar.gz
% wczytujemy dane
load('PrzykladoweDaneSSVEP.mat');
[numberOfTrials numberOfChannels numberOfSamples] = size(X.data);
namesOfChannels = X.channels;
% numberOfChannels numberOfSamples numberOfTrials
W = zeros(numberOfChannels,numberOfChannels);
numberOfHarmonics = 3;
signal = X.data; % ( powtórzenie, kanał, próbki)
S = zeros(size(signal));
W = cosSinCSP(signal,X.stimulation,numberOfHarmonics,X.sampling);
for powt = 1:size(signal,1)
S(powt,:,:) = W'*squeeze(signal(powt,:,:));
end
figure('Name',['Stymulacja: ',num2str(X.stimulation),' Hz'])
for i =1:numberOfChannels
% rysujemy widma uśrednione po realizacjach dla danych
% z oryginalnych kanałów EEG
subplot(2,8,i)
PP=0;
for rep = 1:numberOfTrials
x = squeeze(signal(rep,i,:));
[Pxx,ff] = pwelch(x, X.sampling, 1, X.sampling, X.sampling);
PP =PP + Pxx;
end
plot(ff(ff<60),PP(ff<60))
title(namesOfChannels{i})
% rysujemy widma uśrednione po realizacjach dla danych
% z estymowanych źródeł CSP
subplot(2,8,8+i)
PP=0;
for rep = 1:numberOfTrials
s = squeeze(S(rep,i,:));
[Pss,ff]=pwelch(s, X.sampling, 1, X.sampling, X.sampling);
PP =PP + Pss;
end
plot(ff(ff<60),PP(ff<60))
title(['źródło CSP: ', num2str(i)])
end
ZADANIE: Analiza danych z eksperymentu własnego
- Przefiltruj sygnały EEG w paśmie 1-45 Hz za pomocą procedury filtfilt.
- Na podstawie sygnału trigger oraz danych zapisanych w pliku wyodrębnij sygnały EEG zarejestrowane w trakcie stymulacji z odpowiednimi częstościami.
- Uśrednij sygnały odpowiadające stymulacji tą samą częstością.
- Obejrzyj uśrednione sygnały. (Zaprezentuj je).
- Sposób I:
- Dla każdej realizacji wyestymuj przy pomocy metody Welcha widmo mocy sygnału EEG.
- Dla każdej częstości stymulacji wyznacz poziom tła na podstawie widm pochodzących ze stymulacji innymi częstościami. Np. dla stymulacji częstością 10 Hz poziom tła można wyznaczyć jako 95 centyl ze zbioru wartości widma w częstości 10 Hz dla stymulacji częstościami {4, 7, 13, 16, 20, 25, 30, 35, 40} Hz.
- Dla każdej częstości stymulacji wyznacz miarę odpowiedzi SSVEP (amplitudę widma odpowiadającą częstości stymulacji powyżej poziomy tła dla pojedynczej próby).
- Zaprezentuj widma otrzymane przy stymulacjach różnymi częstościami wraz z korytarzem odpowwiadajacym 95% przedziałowi ufności wyznaczonemu dla widm z pojedynczych realizacji.
- Sporządź wykres odpowiedzi SSVEP od częstości z zaznaczeniem przedziałów ufności i poziomu tła.
- Sposób II:
- Wyestumuj filtr CSP-SSVEP wspólny dla wszystkich częstości stymulacji
- Powtórz kroki ze sposobu I dla uzyskanych komponentów.
- Zaprezentuj filtry przestrzenne i topografie dla poszczególnych komponentów
- Dla przypomnienia:
- Filtr to zestaw współczynników z jakimi należy zsumować sygnały z poszczególnych kanałów EEG aby dostać komponenty odpowiadające hipotetycznym źródłom nieskorelowanym. Filtr można zilustrować na głowie, przypisując poszczególnym pozycjom elektrod wagi równe współrzędnym wektora w (kolumna macierzy W).
- Topografia źródła to zestaw współczynników z jakimi docierają one do poszczególnych kanałów EEG. Topografia zawarta jest w wierszach macierzy odwrotnej do W.
- Można rysunki wykonać jako macierze 5x5 i w pozycji elektrody kolorujemy proporcjonalnie do współczynnika.
- Sposób I:
SSVEP-BCI
W zajęciach tych przydadzą nam się informacje z: https://brain.fuw.edu.pl/edu/index.php/Laboratorium_EEG/Wprowadzenie_do_syg_online
Wstęp
Naszym celem będzie stworzenie prostego interfejsu wykorzystującego zjawisko SSVEP. Po dwóch stronach monitora zamocujemy diody. Każda będzie migać ze swoją ustaloną częstością (np. 16 i 22 Hz) - warto zadbać aby nie były to częstości powiązane ze sobą harmonicznie, a z drugiej strony aby, biorąc pod uwagę wyniki poprzedniego zadania, dawały dobra odpowiedź SSVEP.
Eksperyment będzie miał dwie cześci: sesję kalibracje i sesję on-line. Pomiędzy tymi sesjami będziemy uczyć kalsyfikator. Na podstawie części kalibracyjnej ustalimy jakie parametry przetwarznego on-line sygnału świadczą o patrzeniu się na diodę z lewej a jakie na tą z prawej strony ekranu.
Potem w sesji online będziemy porównywać (za pomocą predykcji klasyfikatora) rejestrowany sygnał z tymi warościami kalibracyjnymi i na tej podstawie system będzie zwracał informację o wyborze lewej lub prawej diody. To powinno umożliwić prostą komunikację na zasadzie pytanie i odpowiedź TAK/NIE.
Sesja kalibracycjna
- Zakładamy czepek
- Częstość próbkowania ustawiamy na 256Hz
- Na podstawie kodu: https://brain.fuw.edu.pl/edu/index.php/Laboratorium_EEG/Wprowadzenie_do_syg_online#.C4.86wiczenie:_Wykorzystanie_pomiaru_EMG_do_sterowania_on-line
tworzymy programik, który zamiast pętli while tworzy odpowiednie pętle for aby:
- pięciokrotnie zarejestrować sekwencję trzech warunków eksperymentalnych:
- patrz 5s na diodę z lewej (warunek l)
- patrz 5s na środek ekranu (warunek s)
- patrz 5s na diodę z prawej (warunek p)
- w czasie tego patrzenia:
- odbieramy próbki w pakietach o długości 0.5s
- każdy pakiet filtrujem (technika filtrowania on-line) w pasmach dookoła wybranych dwóch częstości (PASMO_LEWE / PASMO_PRAWE)
- przefiltrowany pakiet przeliczamy na RMS
- zbieramy sześć zbiorów wyników - zestawy RMSów związane z każdym z waunków kalibracyjnych (LEWY/SPOCZYNEK/PRAWY) dla PASMO_LEWE i PASMO_PRAWE.
- Normalizujemy RMSy. Dla pasma lewego obliczamy (RMS_(l/p/s) - np.mean(RMS_s)) / np.sdt(RMS_s) i analogicznie dla pasma prawego. Małe indeksy oznaczaają tu warunki. Zapamiętujemy współczynniki normalizacyjne.
- Ogladamy rozkłady uzyskanych wielkości (znormalizowanych RMSów).
- Uczymy klasyfikator np. regresję logistyczną (https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegression.html) do rozpoznawania, z którym warunkiem patrzenia mamy do czynienia.
Sesja online
- wczytujemy wyuczony model i kalibracyjne wartości np.mean(RMS_s)) i np.sdt(RMS_s) dla pasm lewego i prawego
- Odbieramy próbki w pakietach o długości 0.5s
- każdy pakiet filtrujem (technika filtrowania on-line) w pasmach dookoła wybranych dwóch częstości (PASMO_LEWE / PASMO_PRAWE)
- przefiltrowany pakiet przeliczamy na RMS
- Normalizujemy RMSy. Dla pasma lewego obliczamy (RMS_(l/p/s) - np.mean(RMS_s)) / np.sdt(RMS_s) i analogicznie dla pasma prawego. Małe indeksy oznaczaają tu warunki.
- robimy predykcję klasyfikatora, z którym warunkiem patrzenia mamy do czynienia. Wyświetlamy na ekranie komunikat.
- Testujemy czy powyższy schemat analizy pozwala na komunikację.
ICA jako filtr przestrzenny
Definicja
Independent Component Analysis (ICA) jest metodą statystycznej analizy sygnałów, która dokonuje dekompozycji wielokanałowych zapisów na składowe niezależne w sensie statystycznym. Dwie składowe s1 i s2 są niezależne jeżeli wiedza o wartości s1 nie daje żadnych informacji o możliwych wartościach s2. ICA może być wyrażona przez prosty model generatywny:
- x = Ds
- gdzie x = {x1, x2, ..., xn} jest zmierzonym n kanałowym sygnałem, D jest macierzą mieszającą zaś s = {s1, s2, ..., sn} jest aktywnością n źródeł. Podstawowym założeniem dotyczącym s jest to, że si są statystycznie niezależne. Aby wyestymować model musimy też założyć, że składowe mają niegaussowskie rozkłady wartości (Hyvärinen, 2000).
Dodatkowo model ten zakłada następujące fakty:
- Sygnał jest liniową mieszaniną aktywności źródeł
- Sygnały pochodzące z każdego ze źródeł są niezależne od pozostałych
- Źródła oraz proces ich mieszania są stacjonarne, tzn, ich momenty statystyczne nie zależą od czasu
- Energie (wariancje) źródeł nie mogą być wyznaczone jednoznacznie. Dzieje się tak ponieważ pomnożenie amplitudy i-tego źródła może być uzyskane poprzez przemnożenie albo si albo przez przemnożenie i-tej kolumny macierzy D. Naturalnym rozwiązaniem tej niejednoznaczności jest wprowadzenie konwencji, że komponenty są normowane tak aby miały wariancję 1: E[si] = 1.
- Kolejność komponentów jest dowolna. Bo jeśli w ten sam sposób zmienimy kolejność komponentów w s i kolumn w D to dostaniemy dokładnie ten sam sygnał x.
Głównym wyzwaniem w analizie ICA jest estymacja macierzy mieszającej D. Gdy jest ona znana to komponenty mogą być wyliczone w następujący sposób:
- s = D−1x
Estymacja
Znalezienie niezależnych komponentów może być rozważane w świetle Centralnego Twierdzenia Granicznego jako poszukiwanie komponentów o możliwie nie gaussowskim rozkładzie. Aby zrozumieć to podejście prześledźmy heurystykę zaproponowaną przez (Hyvärinen, 2000). Dla prostoty załóżmy, że poszukiwane źródła niezależne mają identyczne rozkłady. Zdefiniujmy
y = wTx.
Zauważmy, że jeśli
wT
jest jedną z kolumn macierzy
D−1,
to y jest jednym z poszukiwanych komponentów. Zamieniając zmienne
z = DTw
możemy napisać
y = wTx = wTDs = zTs.
Uwidacznia to fakt, że y jest liniową kombinacją składowych si z wagami danymi przez zi.
Z centralnego twierdzenia granicznego wynika, że suma niezależnych zmiennych losowych ma bardziej gaussowski charakter niż każda z tych zmiennych osobno. Liniowa kombinacja staje się najmniej gaussowska gdy z ma tylko jeden element niezerowy. W tym przypadku y jest proporcjonalny do si. Zatem problem estymacji modelu ICA może być sformułowany jako problem znalezienia takiego wektora w, który maksymalizuje niegaussowskość
y = wTx.
Maksymalizacja niegaussowskości y daje jeden niezależny komponent odpowiadający jednemu z 2n maksimów (bo mamy si i −si) w krajobrazie optymalizacyjnym. Aby znaleźć wszystkie niezależne komponenty musimy znaleźć wszystkie maksima. Ponieważ komponenty są nieskorelowane, to poszukiwania kolejnych komponentów można kontynuować w podprzestrzeni ortogonalnej do już znalezionych komponentów.
Obliczenia
Intuicyjna heurystyka poszukiwania najbardziej niegaussowskich składowych może być użyta do wyprowadzenia różnych funkcji kosztu, których optymalizacja daje model ICA, np. kurtoza.
[math]kurt(y) = E\{y^4\} - 3(E{y^2})^2[/math]
Inną miarą gassowskości jest neg-entropia, którą można wyprowadzić z entropii: Entropia jest miarą średniego zdziwienia wynikiem obserwacji zmiennej losowej: [math]H(Y) = - \sum_i P(Y= a_i) \log(P(Y=a_i)) [/math]
Negentropia jest zdefiniowana:
[math] J(y) = H(y_{gauss}) -H(y)[/math] gdzie [math] y_{gauss} [/math] jest gassuwską zmienną losową o takiej samej kowaiancji jak [math] y [/math].
Negentropia jest skomplikowana obliczeniow, więc w praktyce używana jest formuła przybliżona:
[math] J(y) \varpropto [E\{G (y)\} - E\{G(\nu)\}][/math]
[math]\nu [/math] jest zmienną losową ze standardowego rozkładu normalnego , a G są pewnymi niekwadratowymi funkcjami.
W algorytmie FastICA extremum negentropii jest znajdowane w procedurze bazującej na optymalizacji Netwona. (szczegóły np.: sekcja 6 w https://www.cs.helsinki.fi/u/ahyvarin/papers/NN00new.pdf)
Procedura wykorzystywana w eeglabie („runica”, Makeig 1996) dąży do minimalizacji informacji wzajemnej. Oba podejścia są w przybliżeniu równoważne (Hyvärinen, 2000), chociaż owo przybliżenie dla sygnałów elektrofizjologicznych nie zostało to jeszcze w pełni wyeksplorowane.
Dla sygnałów o niskiej wymiarowości i spełniających dokładnie założenia ICA wszystkie powszechnie wykorzystywane algorytmy dają niemal identyczne wyniki.
- Bardzo ważna uwaga
- ogólną zasadą jest, że jeśli estymujemy N stabilnych komponentów (z N-kanałowych danych) to musimy dysponować kN2 punktami danych w każdym kanale, gdzie N2 jest liczbą elementów w macierzy D, którą ICA próbuje wyestymować, k jest liczbą całkowitą. Nie ma dobrych oszacowań teoretycznych na wielkość k, z praktycznych obserwacji wynika, że rośnie ona z liczbą kanałów.
Możliwe zastosowania
Najczęściej ICA jest stosowana jako narzędzie do:
- usuwania artefaktów z sygnałów EEG (ruchy oczu i mięśnie)
- wydobywania składowych do dalszej analizy (Onton, 2006)
- jako analiza wstępna do lokalizacji źródeł (Grau, 2007).
- ICA jest także stosowana w analize sygnałów EKG i EMG.
Bibliografia
Bazowa praca:
- A. Hyvärinen. Fast and Robust Fixed-Point Algorithms for Independent Component Analysis. IEEE Transactions on Neural Networks 10(3):626-634, 1999 http://www.cs.helsinki.fi/u/ahyvarin/papers/TNN99_reprint.pdf
Nieco prościej opisana wersja z przykładami:
- Hyvärinen, A. and Oja, E. (2000). Independent component analysis: Algorithms and applications. Neural Networks, 13(4-5):411–430.
https://www.cs.helsinki.fi/u/ahyvarin/papers/NN00new.pdf
- Grau, C., Fuentemilla, L., Marco-Pallars, J. (2007). Functional neural dynamics underlying auditory event-related n1 and n1 suppression response. Neuroimage, 36(6):522–31.
- Makeig, S., Bell, A., Jung, T.-P., Sejnowski,T. (1996). Independent component analysis of electroencephalographic data. W: Touretzky, D., Mozer, M., and Hasselmo, M., editors, Advances in Neural Information Processing Systems, volume 8, pages 145–151. MIT Press, Cambridge, MA.
- Onton, J., Makeig, S. (2006). Information-based modeling of event-related brain dynamics. Prog Brain Res., 159:99–120.
- Tutorial: http://sccn.ucsd.edu/wiki/Chapter_09:_Decomposing_Data_Using_ICA
- http://sccn.ucsd.edu/~arno/indexica.html
- http://cis.legacy.ics.tkk.fi/aapo/papers/IJCNN99_tutorialweb/
ZADANIE: Wydobywanie interesujących komponentów
Dane do tej części ćwiczeń proszę pobrać i rozpakować w swoim katalogu: http://www.fuw.edu.pl/~jarekz/LabEEG/Dane_do_ICA_alfa.tar.gz
Pochodzą one z eksperymentu, w którym osoba badana siedziała z zamkniętymi oczami słuchając nagrania czytanego spokojnym głosem. Metadane opisujące sygnał znajdują się w pliku Miro.xml, zaś lokalizacje elektrod w pliku Miro-10-20-Cap.locs.
Proszę:
- wczytać dane do eeglaba
- wyedytować lokalizację elektrod
- usunąć kanały nie zawierające EEG
- zmienić referencje na średnią z kanałów A1 i A2
- przefiltrować filtrem FIR górnoprzepustowym z częstością odcięcia 0,5 Hz
- obejrzeć wstępnie przygotowane dane
- policzyć ICA na całym sygnale
- obejrzeć właściwości otrzymanych komponentów
- Czy są wśród nich takie, które zawierają znaczny udział rytmu alfa?
- Jaka jest ich topografia?
- usunąć wszystkie komponenty nie zawierające alfy
- odtworzyć z tych komponentów sygnał na elektrodach
- wykonać dekompozycję ICA kilkukrotnie (co najmniej 3) i porównać wyniki
- Czy uzyskiwane komponenty są powtarzalne?
- Swoje wyniki porównać też z sąsiednimi grupami.
ZADANIE: Identyfikacja artefaktów
Proszę pobrać dane:
- http://www.fuw.edu.pl/~jarekz/LabEEG/Arousal-10-20-Cap.locs
- http://www.fuw.edu.pl/~jarekz/LabEEG/Arousal1.set
- http://www.fuw.edu.pl/~jarekz/LabEEG/Arousal1.fdt
Pochodzą one z eksperymentu w którym osoba badana czytała słowa o różnych właściwościach wzbudzania emocji.
- wczytaj je do eeglaba
- wczytaj lokalizację kanałów z pliku Arousal-10-20-Cap.locs
- obejrzyj przebiegi czasowe
- odrzuć kanał z diodą (21) i z GSR (20)
- zrób dekompozycję ICA
- obejrzyj topografię komponentów
- zidentyfikuj komponenty odpowiadające mruganiu i aktywności mięśniowej.
- UWAGA
- Aktualnie do wykrywania komponentów artefaktowych warto posłużyć się wtyczkami do eeglaba dostępnymi przez stronę:
https://sccn.ucsd.edu/eeglab/plugin_uploader/plugin_list_all.php
- ICLabel
- MARA
W raporcie:
- zaprezentuj fragmenty sygnału zawierającego artefakty oczne i mięśniowe przed i po zastosowaniu czyszczenia poprzez usuwanie komponentów zdominowanych przez artefakty.
- zaprezentuj topografię i przebiegi czasowe komponentów zidentyfikowanych jako artefakty oczne i mięśniowe.