Obrazowanie:Obrazowanie Medyczne/Scyntygrafia, Tomografia Emisyjna Pojedynczego Fotonu, Pozytonowa Tomografia Emisyjna: Różnice pomiędzy wersjami
| (Nie pokazano 5 wersji utworzonych przez 2 użytkowników) | |||
| Linia 43: | Linia 43: | ||
Przemiana jądra atomowego jest reakcją zachodzącą samorzutnie. Oznacza to, że rozpad danego jądra nie jest powodowany żadnymi czynnikami zewnętrznymi i nie zależy od jego wcześniejszych losów. To, czy w danym momencie czasu nastąpi rozpad danego jądra możemy opisać jedynie z pomocą pojęć statystycznych określając prawdopodobieństwo takiego rozpadu. Do najważniejszych zależności opisujących rozpad promieniotwórczy należą: | Przemiana jądra atomowego jest reakcją zachodzącą samorzutnie. Oznacza to, że rozpad danego jądra nie jest powodowany żadnymi czynnikami zewnętrznymi i nie zależy od jego wcześniejszych losów. To, czy w danym momencie czasu nastąpi rozpad danego jądra możemy opisać jedynie z pomocą pojęć statystycznych określając prawdopodobieństwo takiego rozpadu. Do najważniejszych zależności opisujących rozpad promieniotwórczy należą: | ||
* Prawo rozpadu promieniotwórczego | * Prawo rozpadu promieniotwórczego | ||
| − | <equation> | + | <equation id="eq4"> |
<math> N(t) = N_0e^{-\lambda t} </math> | <math> N(t) = N_0e^{-\lambda t} </math> | ||
:</equation> | :</equation> | ||
| Linia 51: | Linia 51: | ||
:Dodatkowo: <math>\tau = \frac{1}{\lambda}</math> — średni czas życia jądra.<br> | :Dodatkowo: <math>\tau = \frac{1}{\lambda}</math> — średni czas życia jądra.<br> | ||
* Okres połowicznego rozpadu: | * Okres połowicznego rozpadu: | ||
| − | :<equation><math>T_{1/2} = \frac{\ln(2)}{\lambda}</math></equation> | + | :<equation id="eq5"><math>T_{1/2} = \frac{\ln(2)}{\lambda}</math></equation> |
:Gdzie: <br> | :Gdzie: <br> | ||
:<math>T_{1/2}</math> — czas połowicznego zaniku | :<math>T_{1/2}</math> — czas połowicznego zaniku | ||
| Linia 63: | Linia 63: | ||
<math>\tau_b, \lambda_b</math> — to odpowiednio średni czas przebywania radiofarmaceutyku w organizmie pacjenta i stała wydalania radionuklidu z organizmu, <br> | <math>\tau_b, \lambda_b</math> — to odpowiednio średni czas przebywania radiofarmaceutyku w organizmie pacjenta i stała wydalania radionuklidu z organizmu, <br> | ||
Przypominamy, iż stała rozpadu określa prawdopodobieństwo rozpadu cząstki w jednostce czasu. W związku z tym, liczba cząstek radiofarmaceutyku <math>\Delta N_r</math>, która ulegnie przemianie promieniotwórczej w czasie <math>\Delta t</math> wyniesie: | Przypominamy, iż stała rozpadu określa prawdopodobieństwo rozpadu cząstki w jednostce czasu. W związku z tym, liczba cząstek radiofarmaceutyku <math>\Delta N_r</math>, która ulegnie przemianie promieniotwórczej w czasie <math>\Delta t</math> wyniesie: | ||
| − | <equation><math> | + | <equation id="eq6"><math> |
\Delta N_r = -\lambda_r N\Delta t | \Delta N_r = -\lambda_r N\Delta t | ||
</math></equation> | </math></equation> | ||
z kolei liczba cząstek radiofarmaceutyku <math>\Delta N_b</math> wydalonych z organizmu w czasie <math>\Delta t</math> jest równa: | z kolei liczba cząstek radiofarmaceutyku <math>\Delta N_b</math> wydalonych z organizmu w czasie <math>\Delta t</math> jest równa: | ||
| − | <equation><math> | + | <equation id="eq7"><math> |
\Delta N_b = -\lambda_b N\Delta t | \Delta N_b = -\lambda_b N\Delta t | ||
</math></equation> | </math></equation> | ||
Ostatecznie, w ciągu czasu <math>\Delta t</math> liczba cząstek <math>\Delta N</math> która ulegnie rozpadowi lub wydaleniu z organizmu wynosi: | Ostatecznie, w ciągu czasu <math>\Delta t</math> liczba cząstek <math>\Delta N</math> która ulegnie rozpadowi lub wydaleniu z organizmu wynosi: | ||
| − | <equation><math> | + | <equation id="eq8"><math> |
\Delta N = \Delta N_r + \Delta N_b = -(\lambda_r + \lambda_b) N\Delta t | \Delta N = \Delta N_r + \Delta N_b = -(\lambda_r + \lambda_b) N\Delta t | ||
</math></equation> | </math></equation> | ||
Przechodząc w granicy do małych przyrostów <math>\Delta N</math> i <math>\Delta t</math> otrzymujemy następujące równanie różniczkowe: | Przechodząc w granicy do małych przyrostów <math>\Delta N</math> i <math>\Delta t</math> otrzymujemy następujące równanie różniczkowe: | ||
| − | <equation> | + | <equation id="eq9"> |
<math> dN = -(\lambda_r + \lambda_b) N dt</math> | <math> dN = -(\lambda_r + \lambda_b) N dt</math> | ||
</equation> | </equation> | ||
którego rozwiązaniem jest następująca zależność: | którego rozwiązaniem jest następująca zależność: | ||
| − | <equation> | + | <equation id="eq10"> |
<math> N(t) = N_0e^{-(\lambda_r + \lambda_b)t}</math> | <math> N(t) = N_0e^{-(\lambda_r + \lambda_b)t}</math> | ||
</equation> | </equation> | ||
| Linia 87: | Linia 87: | ||
Możemy wprowadzić wypadkową, efektywną stałą rozpadu, uwzględniająca proces rozpadu promieniotwórczego oraz procesy wydalania radiofarmaceutyku z organizmu: | Możemy wprowadzić wypadkową, efektywną stałą rozpadu, uwzględniająca proces rozpadu promieniotwórczego oraz procesy wydalania radiofarmaceutyku z organizmu: | ||
| − | <equation> | + | <equation id="eq11"> |
<math> \lambda_e = \lambda_r + \lambda_b</math> | <math> \lambda_e = \lambda_r + \lambda_b</math> | ||
</equation> | </equation> | ||
i odpowiadający jej średni czas życia radionuklidu w organizmie pacjenta: | i odpowiadający jej średni czas życia radionuklidu w organizmie pacjenta: | ||
| − | <equation> | + | <equation id="eq12"> |
<math> \frac{1}{\tau_e} = \frac{1}{\tau_r} +\frac{1}{\tau_b}</math> | <math> \frac{1}{\tau_e} = \frac{1}{\tau_r} +\frac{1}{\tau_b}</math> | ||
</equation> | </equation> | ||
Po przekształceniu ostatniego wzoru otrzymujemy: | Po przekształceniu ostatniego wzoru otrzymujemy: | ||
| − | <equation> | + | <equation id="eq13"> |
<math> \tau_e = \frac{\tau_r\cdot \tau_b}{\tau_r+\tau_b}</math> | <math> \tau_e = \frac{\tau_r\cdot \tau_b}{\tau_r+\tau_b}</math> | ||
</equation> | </equation> | ||
Wykorzystując zależność pomiędzy stałą rozpadu i średnim czasem życia dostajemy okres efektywny połowicznego rozpadu promieniotwórczego w organizmie: | Wykorzystując zależność pomiędzy stałą rozpadu i średnim czasem życia dostajemy okres efektywny połowicznego rozpadu promieniotwórczego w organizmie: | ||
| − | <equation> | + | <equation id="eq14"> |
<math> T^{1/2}_e = \frac{T^{1/2}_r\cdot T^{1/2}_b}{T^{1/2}_r+T^{1/2}_b}</math> | <math> T^{1/2}_e = \frac{T^{1/2}_r\cdot T^{1/2}_b}{T^{1/2}_r+T^{1/2}_b}</math> | ||
</equation> | </equation> | ||
W przypadku, gdy do zebrania informacji niezbędnej do utworzenia obrazu diagnostycznego wymagany jest okres czasu <math>T^d</math>, czas efektywnego rozpadu radiofarmaceutyku powinien być w przybliżeniu równy czasowi <math>T^d</math>. Jeśli zastosowany do badania radiofarmaceutyk usuwany jest z organizmu z czasem połowicznego wydalania <math>T^{1/2}_b</math>, to radionuklid wchodzący w skład radiofarmaceutyku powinien charakteryzować się czasem połowicznego rozpadu równym: | W przypadku, gdy do zebrania informacji niezbędnej do utworzenia obrazu diagnostycznego wymagany jest okres czasu <math>T^d</math>, czas efektywnego rozpadu radiofarmaceutyku powinien być w przybliżeniu równy czasowi <math>T^d</math>. Jeśli zastosowany do badania radiofarmaceutyk usuwany jest z organizmu z czasem połowicznego wydalania <math>T^{1/2}_b</math>, to radionuklid wchodzący w skład radiofarmaceutyku powinien charakteryzować się czasem połowicznego rozpadu równym: | ||
| − | <equation> | + | <equation id="eq15"> |
<math> T^{1/2}_r = \frac{T^{d}\cdot T^{1/2}_b}{T^{d}+T^{1/2}_b}</math> | <math> T^{1/2}_r = \frac{T^{d}\cdot T^{1/2}_b}{T^{d}+T^{1/2}_b}</math> | ||
</equation> | </equation> | ||
| Linia 121: | Linia 121: | ||
[[File:gamma_camera_spectrum_3.png|300px|thumb|right|<figure id="fig:gamma_camera_spectrum_3"></figure>Fotopik oraz składowa widma promieniowania γ powstała w wyniku rozpraszania Comptonowskiego w krysztale scyntylacyjnym. Składowa Comptonowska gwałtownie zanika dla energii powyżej pewnego progu. Zanik ten nazywamy krawędzią Comptonowską. Linią przerywaną narysowano przebieg przykładowej rzeczywistej krawędzi Comptonowskiej. ]] | [[File:gamma_camera_spectrum_3.png|300px|thumb|right|<figure id="fig:gamma_camera_spectrum_3"></figure>Fotopik oraz składowa widma promieniowania γ powstała w wyniku rozpraszania Comptonowskiego w krysztale scyntylacyjnym. Składowa Comptonowska gwałtownie zanika dla energii powyżej pewnego progu. Zanik ten nazywamy krawędzią Comptonowską. Linią przerywaną narysowano przebieg przykładowej rzeczywistej krawędzi Comptonowskiej. ]] | ||
| − | [[File:gamma_camera_spectrum_4.png|300px|thumb|right|<figure id="fig:gamma_camera_spectrum_4"></figure>Fotopik, składowa widma promieniowania γ powstała w wyniku rozpraszania Comptonowskiego w krysztale scyntylacyjnym oraz składowa widma powstała w wyniku rozpraszania Comptonowskiego fotonów γ w ciele pacjenta.]] | + | [[File:gamma_camera_spectrum_4.png|300px|thumb|right|<figure id="fig:gamma_camera_spectrum_4"></figure>Fotopik, składowa widma promieniowania γ powstała w wyniku rozpraszania Comptonowskiego w krysztale scyntylacyjnym oraz składowa widma powstała w wyniku wielokrotnego rozpraszania Comptonowskiego fotonów γ w ciele pacjenta.]] |
[[File:gamma_camera_spectrum_5.png|300px|thumb|right|<figure id="fig:gamma_camera_spectrum_5"></figure>Składowe widma powstające w wyniku oddziaływania fotonów z materią w różnych procesach nakładają się na siebie prowadząc do rozmycia najbardziej istotnej składowej widma — fotopiku (linia przerywana).]] | [[File:gamma_camera_spectrum_5.png|300px|thumb|right|<figure id="fig:gamma_camera_spectrum_5"></figure>Składowe widma powstające w wyniku oddziaływania fotonów z materią w różnych procesach nakładają się na siebie prowadząc do rozmycia najbardziej istotnej składowej widma — fotopiku (linia przerywana).]] | ||
| Linia 144: | Linia 144: | ||
Rozmycie fotopiku nie jest jedynym problemem, który utrudnia prawidłowe określenie natężenia fotonów γ w funkcji energii. Kwant promieniowania γ wytworzony w wyniku rozpadu znacznika w radiofarmaceutyku, zanim dotrze do scyntylatora, może ulec procesom które zmienią jego energię. W niniejszych materiałach opiszemy dwa najważniejsze zjawiska, prowadzące do zmiany energii fotonów γ | Rozmycie fotopiku nie jest jedynym problemem, który utrudnia prawidłowe określenie natężenia fotonów γ w funkcji energii. Kwant promieniowania γ wytworzony w wyniku rozpadu znacznika w radiofarmaceutyku, zanim dotrze do scyntylatora, może ulec procesom które zmienią jego energię. W niniejszych materiałach opiszemy dwa najważniejsze zjawiska, prowadzące do zmiany energii fotonów γ | ||
Pierwszym zjawiskiem jest rozpraszania Comptonowskie, które zachodzi na atomach scyntylatora. Energię rozproszonego w procesie Comptonowskim fotonu określa następujący wzór: | Pierwszym zjawiskiem jest rozpraszania Comptonowskie, które zachodzi na atomach scyntylatora. Energię rozproszonego w procesie Comptonowskim fotonu określa następujący wzór: | ||
| − | <equation> | + | <equation id = “eq20”> |
<math>E'=\frac{E}{1 + \frac{E}{m_ec^2}(1-\cos(\Theta))} </math> | <math>E'=\frac{E}{1 + \frac{E}{m_ec^2}(1-\cos(\Theta))} </math> | ||
</equation> | </equation> | ||
| Linia 154: | Linia 154: | ||
W przypadku gdy kierunek ruchu fotonu wtórnego jest przeciwny do kierunku ruchu padającego, mówimy o rozpraszaniu wstecznym. | W przypadku gdy kierunek ruchu fotonu wtórnego jest przeciwny do kierunku ruchu padającego, mówimy o rozpraszaniu wstecznym. | ||
Kąt <math>\Theta</math> wynosi wtedy 180 stopni, zaś energia fotonu rozproszonego wynosi: | Kąt <math>\Theta</math> wynosi wtedy 180 stopni, zaś energia fotonu rozproszonego wynosi: | ||
| − | <equation> | + | <equation id = “eq21”> |
<math>E'=\frac{E}{1 + 2\frac{E}{m_ec^2}} </math> | <math>E'=\frac{E}{1 + 2\frac{E}{m_ec^2}} </math> | ||
</equation> | </equation> | ||
Energia zdeponowana przez foton padający w krysztale scyntylacyjnym jest równa | Energia zdeponowana przez foton padający w krysztale scyntylacyjnym jest równa | ||
różnicy energii fotonu padającego i fotonu rozproszonego. W przypadku rozpraszania wstecznego jest ona równa: | różnicy energii fotonu padającego i fotonu rozproszonego. W przypadku rozpraszania wstecznego jest ona równa: | ||
| − | <equation> | + | <equation id = “eq22”> |
<math>\Delta E = E - E'=\frac{E^2}{E+255,2}[keV] </math> | <math>\Delta E = E - E'=\frac{E^2}{E+255,2}[keV] </math> | ||
</equation> | </equation> | ||
| Linia 165: | Linia 165: | ||
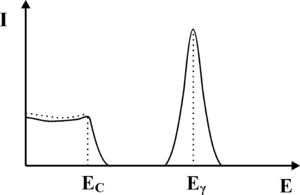
Zauważmy, iż jeśli foton ulega rozproszeniu Comptonowskiego, to może on zdeponować najwięcej energii w krysztale scyntylacyjnym właśnie w trakcie rozpraszania wstecznego. Przekaz większej energii do kryształu scyntylacyjnego w wyniku pojedynczego akty rozpraszania Comptonowskiego jest niemożliwy. Przykładowo, jeśli na do kryształu scyntylacyjnego docierają fotony γ o energi <math>E_{\gamma} = 140</math> keV (emitowane przez Technet), to fotony wtórne powstałe w wyniku wstecznego rozpraszania Comptonowskiego będą miały energię 90 keV, zaś w krysztale zostanie zdeponowana energia 50 keV. Rozpraszanie Comptonowskie, jest zatem nie tylko odpowiedzialne za produkcję fotonów wtórnych, które prowadzą do poszerzenia fotopiku lecz także formują nową składową widma uzyskiwanego z detektora scyntylacyjnego. Składowa ta, którą określa się jako składową Comptonowską, została zaprezentowana na rysunku <xr id="fig:gamma_camera_spectrum_3">rys. %i</xr>. Jej charakterystyczną cechą jest gwałtowny zanik, dla energii wyższych niż pewien próg, którym jest energia zdeponowana przez fotony γ w krysztale, w trakcie wstecznego rozpraszania Comptonowskiego. Próg ten nazwano krawędzią Comptonowską. Krawędź ta w rzeczywistym widmie jest nie znacznie rozmyta, co ponownie jest związane ze statystycznym charakterem zjawisk, które prowadzą do jej utworzenia. | Zauważmy, iż jeśli foton ulega rozproszeniu Comptonowskiego, to może on zdeponować najwięcej energii w krysztale scyntylacyjnym właśnie w trakcie rozpraszania wstecznego. Przekaz większej energii do kryształu scyntylacyjnego w wyniku pojedynczego akty rozpraszania Comptonowskiego jest niemożliwy. Przykładowo, jeśli na do kryształu scyntylacyjnego docierają fotony γ o energi <math>E_{\gamma} = 140</math> keV (emitowane przez Technet), to fotony wtórne powstałe w wyniku wstecznego rozpraszania Comptonowskiego będą miały energię 90 keV, zaś w krysztale zostanie zdeponowana energia 50 keV. Rozpraszanie Comptonowskie, jest zatem nie tylko odpowiedzialne za produkcję fotonów wtórnych, które prowadzą do poszerzenia fotopiku lecz także formują nową składową widma uzyskiwanego z detektora scyntylacyjnego. Składowa ta, którą określa się jako składową Comptonowską, została zaprezentowana na rysunku <xr id="fig:gamma_camera_spectrum_3">rys. %i</xr>. Jej charakterystyczną cechą jest gwałtowny zanik, dla energii wyższych niż pewien próg, którym jest energia zdeponowana przez fotony γ w krysztale, w trakcie wstecznego rozpraszania Comptonowskiego. Próg ten nazwano krawędzią Comptonowską. Krawędź ta w rzeczywistym widmie jest nie znacznie rozmyta, co ponownie jest związane ze statystycznym charakterem zjawisk, które prowadzą do jej utworzenia. | ||
| − | Kolejna składowa widma promieniowania γ uzyskiwana w detektorze scyntylacyjnym jest również związana z rozpraszaniem Comptonowskim fotonów, ale zachodzącym w organizmie pacjenta. Jak pamiętamy z materiałów dotyczących promieniowania rentgenowskiego, | + | Kolejna składowa widma promieniowania γ uzyskiwana w detektorze scyntylacyjnym jest również związana z rozpraszaniem Comptonowskim fotonów, ale zachodzącym w organizmie pacjenta. Jej kształt będzie zależał między innymi od grubości badanego przedmiotu. W cienkim przedmiocie będą dominowały fotony, które uległy pojedynczemu rozproszeniu Comptonowskiemu, a zatem ich minimalna energia wynosi w wypadku technetu 90 keV. W praktyce jednak w pacjencie większe znaczenie mogą odegrać fotony rozproszone wielokrotnie, których energia końcowa może być znacznie niższa. Jak pamiętamy z materiałów dotyczących promieniowania rentgenowskiego, promieniowanie elektromagnetyczne o energii poniżej 10 keV jest silnie tłumione przez ciało człowieka, dlatego nie zaobserwujemy fotonów γ rozproszonych Comptonowsko o energiach poniżej tego progu. Pozostałe fotony, które uległy oddziaływaniu Comptonowskiego, będą miały energię z zakresu od około 10-20keV do maksymalnej energii, jaką dany foton może uzyskać w wyniku rozpadu promieniotwórczego. Fotony te, oddziałując ze scyntylatorem uformują składową widma zaprezentowaną na <xr id="fig:gamma_camera_spectrum_4">rys. %i</xr>. |
Fotony emitowane z radiofarmaceutyku mogą brać udział również w innych procesach (np. ulegać rozpraszaniu Comptonowskiemu w ołowianym kolimatorze założonym na detektor) prowadząc do powstawania kolejnych składowych widma. Proces te nie będą tutaj omawiane. Należy jednak pamiętać, iż widma te mogą nakładać się na fotopik, prowadząc do jego zniekształcenia, co zaprezentowano na rysunku <xr id="fig:gamma_camera_spectrum_5">rys. %i</xr>. | Fotony emitowane z radiofarmaceutyku mogą brać udział również w innych procesach (np. ulegać rozpraszaniu Comptonowskiemu w ołowianym kolimatorze założonym na detektor) prowadząc do powstawania kolejnych składowych widma. Proces te nie będą tutaj omawiane. Należy jednak pamiętać, iż widma te mogą nakładać się na fotopik, prowadząc do jego zniekształcenia, co zaprezentowano na rysunku <xr id="fig:gamma_camera_spectrum_5">rys. %i</xr>. | ||
| Linia 245: | Linia 245: | ||
* Czułość gamma-kamery. | * Czułość gamma-kamery. | ||
:Czułość gamma-kamery zdefiniowana jest w następujący sposób: | :Czułość gamma-kamery zdefiniowana jest w następujący sposób: | ||
| − | :<equation><math> | + | :<equation id = “eq23”><math> |
sensitivity = \frac{N_o}{N_a} | sensitivity = \frac{N_o}{N_a} | ||
</math></equation> | </math></equation> | ||
| Linia 254: | Linia 254: | ||
* Rozdzielczość gamma-kamery | * Rozdzielczość gamma-kamery | ||
:Przypominamy, że rozdzielczość układu obrazującego to jego zdolność do zaprezentowania dwóch punktów znajdujących się w pewnej odległości od siebie, jako dwóch oddzielnych obiektów na obrazie. Na <xr id="fig:kolimator_0">rys. %i</xr> widzimy, że dana septa w kolimatorze przepuszcza do scyntylatora fotony pochodzące z obszaru o długości <math>d</math>. W związku z tym, wszystkie punkty znajdujące się w obrębie tego obszaru zostaną na obrazie zaprezentowane jako jeden punkt. Parametr <math>d</math> określa zatem rozdzielczość kolimatora. Z prostych relacji geometrycznych, uzyskamy następującą zależność parametru <math>d</math> od głębokości ''h'' i szerokości ''s'' septy oraz odległości ''l'' kryształu scyntylacyjnego od badanego obszaru: | :Przypominamy, że rozdzielczość układu obrazującego to jego zdolność do zaprezentowania dwóch punktów znajdujących się w pewnej odległości od siebie, jako dwóch oddzielnych obiektów na obrazie. Na <xr id="fig:kolimator_0">rys. %i</xr> widzimy, że dana septa w kolimatorze przepuszcza do scyntylatora fotony pochodzące z obszaru o długości <math>d</math>. W związku z tym, wszystkie punkty znajdujące się w obrębie tego obszaru zostaną na obrazie zaprezentowane jako jeden punkt. Parametr <math>d</math> określa zatem rozdzielczość kolimatora. Z prostych relacji geometrycznych, uzyskamy następującą zależność parametru <math>d</math> od głębokości ''h'' i szerokości ''s'' septy oraz odległości ''l'' kryształu scyntylacyjnego od badanego obszaru: | ||
| − | :<equation><math> | + | :<equation id = “eq24”><math> |
d = 2\frac{(l + h)s}{h} -s= 2s(1+\frac{l}{h}) -s | d = 2\frac{(l + h)s}{h} -s= 2s(1+\frac{l}{h}) -s | ||
</math></equation> | </math></equation> | ||
| Linia 352: | Linia 352: | ||
Cząstka ta w wyniku rozpadu uzyskuje pewną energię, którą wytraca w oddziaływaniach z otoczeniem. Po zwolnieniu do prędkości termicznych, pozyton anihiluje z elektronem znajdującym się w otoczeniu. W wyniku anihilacji powstają (w zdecydowanej ilości przypadków) dwa fotony γ, które w układzie środka masy rozbiegają się w przeciwnych kierunkach. W układzie laboratoryjnym istnieją mierzalne odstępstwa od przeciwnego kierunku ruchu kwantów γ, jednak zwykle są one pomijane. Fotony po dotarciu do detektorów promieniowania są rejestrowane. Do tworzenia obrazu wykorzystywane są te pary kwantów γ, które jednocześnie dotarły do detektorów. Innymi słowy, w metodzie PET detekcji podlegają koincydencje czasowe dotarcie kwantów γ do detektorów. Poniżej wypisano przemiany fizyczne prowadzące do emisji dwóch fotonów γ. | Cząstka ta w wyniku rozpadu uzyskuje pewną energię, którą wytraca w oddziaływaniach z otoczeniem. Po zwolnieniu do prędkości termicznych, pozyton anihiluje z elektronem znajdującym się w otoczeniu. W wyniku anihilacji powstają (w zdecydowanej ilości przypadków) dwa fotony γ, które w układzie środka masy rozbiegają się w przeciwnych kierunkach. W układzie laboratoryjnym istnieją mierzalne odstępstwa od przeciwnego kierunku ruchu kwantów γ, jednak zwykle są one pomijane. Fotony po dotarciu do detektorów promieniowania są rejestrowane. Do tworzenia obrazu wykorzystywane są te pary kwantów γ, które jednocześnie dotarły do detektorów. Innymi słowy, w metodzie PET detekcji podlegają koincydencje czasowe dotarcie kwantów γ do detektorów. Poniżej wypisano przemiany fizyczne prowadzące do emisji dwóch fotonów γ. | ||
#Radionuklid w radiofarmaceutyku ulega rozpadowi <math>\beta^+</math> | #Radionuklid w radiofarmaceutyku ulega rozpadowi <math>\beta^+</math> | ||
| − | <equation><math> | + | <equation id = “eq25”><math> |
_Z^AX\rightarrow _{Z-1}^AX + e^+ + \nu</math> | _Z^AX\rightarrow _{Z-1}^AX + e^+ + \nu</math> | ||
</equation> | </equation> | ||
W trakcie przemiany, pozyton uzyskuje pewną energię kinetyczną, po wytraceniu której, zwalnia do prędkości termicznych, a następnie anihiluje z przypadkowym elektronem: | W trakcie przemiany, pozyton uzyskuje pewną energię kinetyczną, po wytraceniu której, zwalnia do prędkości termicznych, a następnie anihiluje z przypadkowym elektronem: | ||
| − | <equation><math> | + | <equation id = “eq26”><math> |
e^+ + e^{-} = 2\gamma</math> | e^+ + e^{-} = 2\gamma</math> | ||
</equation> | </equation> | ||
| Linia 420: | Linia 420: | ||
|} | |} | ||
Jak widzimy, radionuklidem o stosunkowo długim okresie połowicznego rozpadu oraz niskiej energii emitowanych pozytonów jest izotop fluoru. Jest on najczęściej stosowanym znacznikiem w radiofarmaceutykach. Dołączony do glukozy (nośnika) tworzy radiofarmaceutyk fluorodeoksyglukozę (FDA). Niestety, problem stanowi praktyczne otrzymywanie izotopu <math>^{18}F</math>. Radionuklid ten można otrzymać w cyklotronach w wyniku bombardowania przyspieszanymi protonami tarczy zawierającej tlen: | Jak widzimy, radionuklidem o stosunkowo długim okresie połowicznego rozpadu oraz niskiej energii emitowanych pozytonów jest izotop fluoru. Jest on najczęściej stosowanym znacznikiem w radiofarmaceutykach. Dołączony do glukozy (nośnika) tworzy radiofarmaceutyk fluorodeoksyglukozę (FDA). Niestety, problem stanowi praktyczne otrzymywanie izotopu <math>^{18}F</math>. Radionuklid ten można otrzymać w cyklotronach w wyniku bombardowania przyspieszanymi protonami tarczy zawierającej tlen: | ||
| − | <equation><math> | + | <equation id = “eq26”><math> |
^{18}\mathrm{O} + \mathrm{p} \rightarrow ^{18}\mathrm{F} + \mathrm{n} | ^{18}\mathrm{O} + \mathrm{p} \rightarrow ^{18}\mathrm{F} + \mathrm{n} | ||
</math ></equation> | </math ></equation> | ||
| Linia 426: | Linia 426: | ||
==Konstrukcja Tomografu PET== | ==Konstrukcja Tomografu PET== | ||
| − | Zdjęcia tomografów PET, schematy ich budowy jak i uzyskiwane za ich pomocą obrazy można zobaczyć w [[ | + | Zdjęcia tomografów PET, schematy ich budowy jak i uzyskiwane za ich pomocą obrazy można zobaczyć w [[wikipedia:Pozytonowa_emisyjna_tomografia_komputerowa|na stronie w Wikipedii]]. Skaner PET składa się z bardzo wielu detektorów scyntylacyjnych ułożonych na obwodzie pierścienia w środku którego znajduje się badana osoba. Zwykle tomograf posiada kilka rzędów takich pierścieni. O ile kryształy scyntylacyjne mogę bardzo małe rozmiary, to fotopowielacze charakteryzują się relatywnie dużymi średnicami. W celu umieszczenia na obwodzie jak największej liczby detektorów stosuje się następujące rozwiązanie. Fotopowielacze łączone są w bloki (np. po 4 sztuki) i umieszczane na jednym krysztale scyntylacyjnym. W celu zwiększenia precyzji określenia błysku scyntylacyjnego, w krysztale wykonywane są nacięcia o odpowiednio dobranej głębokości, które zostają wypełnione materiałem odbijającym światło. Fala elektromagnetyczna emitowana w błysku scyntylacyjnym odbija się na wykonanych nacięciach, co ogranicza jego transmisję w dowolnych kierunkach. Liczba opisanych detektorów umieszczonych na obwodzie pierścienia wynosi od 100 do około 1000 sztuk, zaś w jednym skanerze PET zainstalowanych jest od 16 do 32 pierścieni. |
==Wady i zalety PET.== | ==Wady i zalety PET.== | ||
Aktualna wersja na dzień 11:47, 29 sty 2018
Scyntygrafia, Tomografia Emisyjna Pojedynczego Fotonu, Pozytonowa Tomografia Emisyjna
Scyntygrafia, Komputerowa Tomografia Emisyjna Pojedynczego Fotonu (ang. Single Photon Emmision Computed Tomograpy, SPECT) oraz Pozytonowa Tomografia Emisyjna (ang. Positron Emission Tomography) to metody tzw. Medycyny Nuklearnej. Różnią się one co do sposobu i jakości otrzymywanego obrazu — w scyntygrafii uzyskuje się obraz planarny, podczas gdy w metodzie SPECT i PET obrazy wybranych warstw pacjenta. Cechą, która łączy wymienione metody to stosowanie w procesie obrazowania tzw. radiofarmaceutyków.
Spis treści
- 1 Radiofarmaceutyki
- 2 Prawo rozpadu promieniotwórczego
- 3 Dobór nuklidów radio-promieniotwórczych w obrazowaniu medycznym
- 4 Detektory promieniowania γ
- 5 Budowa Gamma Kamery
- 6 Tomografia Emisyjna Pojedynczego Fotonu (ang. Single Photon Emission Tomography, SPECT)
- 7 Pozytonowa Emisyjna Tomografia Komputerowa (ang. Positron Emission Tomography, PET)
- 8 Konstrukcja Tomografu PET
- 9 Wady i zalety PET.
Radiofarmaceutyki
Radiofarmaceutyk jest związkiem chemicznym składającym się z dwóch zasadniczych elementów:
- Znacznika, którym jest odpowiednio dobrany radionuklid.
- Nośnika, którym jest związek chemiczny posiadający zdolność osadzania się w odpowiednich tkankach czy narządach, bądź też jest wychwytywany przez komórki np. zmienione chorobowo.
Produkty rozpadu promieniotwórczego radiofarmaceutyku mogą być rejestrowane za pomocą odpowiedniej aparatury, dając w ten sposób informację o jego lokalizacji. W omawianych metodach obraz diagnostyczny reprezentuje zatem mapę rozkładu radiofarmaceutyku w organizmie lub narządach pacjenta.
Przemiany Promieniotwórcze
Spośród wielu przemian promieniotwórczych, które zachodzą w przyrodzie, w diagnostyce medycznej stosowane są dwie:
- Przemiana Gamma, która towarzyszy praktycznie każdej innej przemianie jądrowej. W jej wyniku liczba atomowa i masowa jądra atomowego pozostają niezmienione, zmianie ulega natomiast energia wzbudzonego jądra. Promieniowanie gamma jest promieniowaniem elektromagnetycznym (jest to emisja fotonu z wzbudzonego jądra). Widmo energii promieniowania gamma jest dyskretne. Przemianę Gamma można zapisać w następujący sposób:
gdzie:
[math]_Z^AX^*[/math] — jądro w stanie wzbudzonym o liczbie masowej A i atomowej Z.
[math]_Z^AX[/math] — jądro o liczbie masowej A i atomowej Z w stanie podstawowym.
Jak wspomniano, przemiana ta towarzyszy w zasadzie każdym innym przemianom promieniotwórczym, w wyniku których jądro atomowe zostaje wzbudzone.
- Przemiana Beta[math]^+[/math]. W tej reakcji proton z jądra atomowego ulega przemianie w neutron, zgodnie z poniższym wzorem:
gdzie:
p — proton,
n — neutron,
[math]e^+[/math] — pozyton,
[math]\nu[/math] — neutrino elektronowe.
W konsekwencji, jądro atomowe zmniejsza swój ładunek o jeden:
W przemianie Beta[math]^+[/math] dochodzi do przemiany lżejszego neutronu w cięższy proton, dlatego jest ona energetycznie mniej korzystna niż znana ze szkoły średniej przemiana Beta[math]^-[/math]. Aby rozpad zaszedł, musi być dostarczona energia z zewnątrz (nie może zajść w próżni, natomiast może zajść w jądrze atomowym). Z uwagi na emisję trzech produktów w trakcie przemiany, widmo energii kinetycznej pozytonu, jaką uzyskuje on w trakcie rozpadu jest ciągłe. Pozyton nie może osiągnąć jednak energii większej niż pewna wartość maksymalna, charakterystyczna dla przemiany danego nuklidu.
Prawo rozpadu promieniotwórczego
Przemiana jądra atomowego jest reakcją zachodzącą samorzutnie. Oznacza to, że rozpad danego jądra nie jest powodowany żadnymi czynnikami zewnętrznymi i nie zależy od jego wcześniejszych losów. To, czy w danym momencie czasu nastąpi rozpad danego jądra możemy opisać jedynie z pomocą pojęć statystycznych określając prawdopodobieństwo takiego rozpadu. Do najważniejszych zależności opisujących rozpad promieniotwórczy należą:
- Prawo rozpadu promieniotwórczego
- Okres połowicznego rozpadu:
- [math]T_{1/2} = \frac{\ln(2)}{\lambda}[/math]
- Gdzie:
- [math]T_{1/2}[/math] — czas połowicznego zaniku
Dobór nuklidów radio-promieniotwórczych w obrazowaniu medycznym
Utworzenia mapy rozkładu radiofarmaceutyku w organizmie człowieka wymaga zebrania odpowiedniej ilości danych. Radionuklid, nie może zatem charakteryzować się zbyt krótkim czasem połowicznego rozpadu. Z drugiej strony, materiał promieniotwórczy powinien być jak najszybciej wydalony z organizmu człowieka, aby zminimalizować dawkę promieniowania jonizującego na które narażona jest badana osoba. Dobór odpowiedniego znacznika i nośnika, które spełnią powyższe oczekiwania jest bardzo trudny, a dziedziną którą zajmuje się wspomnianymi związkami jest radiochemia. Poniżej wymienimy trzy najważniejsze cechy jakimi powinien charakteryzować się radionuklid promieniotwórczy wybrany jako znacznik.
Czas połowicznego rozpadu i efektywny czas połowicznego rozpadu.
Dostępny okres czasu, w trakcie którego można zbierać dane niezbędne do utworzenia mapy rozkładu radiofarmaceutyku w organizmie człowieka zależy głównie od dwóch wielkości: tempa zachodzenia rozpadu promieniotwórczego oraz szybkości wydalania radiofarmaceutyku z organizmu. Wprowadźmy następujące oznaczenia:
[math]\tau_r, \lambda_r[/math] — to odpowiednio średni czas życia i stała rozpadu radionuklidu,
[math]\tau_b, \lambda_b[/math] — to odpowiednio średni czas przebywania radiofarmaceutyku w organizmie pacjenta i stała wydalania radionuklidu z organizmu,
Przypominamy, iż stała rozpadu określa prawdopodobieństwo rozpadu cząstki w jednostce czasu. W związku z tym, liczba cząstek radiofarmaceutyku [math]\Delta N_r[/math], która ulegnie przemianie promieniotwórczej w czasie [math]\Delta t[/math] wyniesie:
z kolei liczba cząstek radiofarmaceutyku [math]\Delta N_b[/math] wydalonych z organizmu w czasie [math]\Delta t[/math] jest równa:
Ostatecznie, w ciągu czasu [math]\Delta t[/math] liczba cząstek [math]\Delta N[/math] która ulegnie rozpadowi lub wydaleniu z organizmu wynosi:
Przechodząc w granicy do małych przyrostów [math]\Delta N[/math] i [math]\Delta t[/math] otrzymujemy następujące równanie różniczkowe:
którego rozwiązaniem jest następująca zależność:
gdzie:
[math]N(t)[/math] — liczba cząstek radiofarmaceutyku, która nie uległa rozpadowi lub wydaleniu z organizmu po czasie [math]t[/math].
[math]N_0[/math] — początkowa liczba cząstek radiofarmaceutyku.
Możemy wprowadzić wypadkową, efektywną stałą rozpadu, uwzględniająca proces rozpadu promieniotwórczego oraz procesy wydalania radiofarmaceutyku z organizmu:
i odpowiadający jej średni czas życia radionuklidu w organizmie pacjenta:
Po przekształceniu ostatniego wzoru otrzymujemy:
Wykorzystując zależność pomiędzy stałą rozpadu i średnim czasem życia dostajemy okres efektywny połowicznego rozpadu promieniotwórczego w organizmie:
W przypadku, gdy do zebrania informacji niezbędnej do utworzenia obrazu diagnostycznego wymagany jest okres czasu [math]T^d[/math], czas efektywnego rozpadu radiofarmaceutyku powinien być w przybliżeniu równy czasowi [math]T^d[/math]. Jeśli zastosowany do badania radiofarmaceutyk usuwany jest z organizmu z czasem połowicznego wydalania [math]T^{1/2}_b[/math], to radionuklid wchodzący w skład radiofarmaceutyku powinien charakteryzować się czasem połowicznego rozpadu równym:
Przyjmuje się, że efektywny czas półtrwania radiofarmaceutyka powinien być około 1,5 razy dłuższy niż czas procedury badania. Kryterium to jest jednak spełnione tylko dla niektórych radiofarmaceutyków.
Detektory promieniowania γ
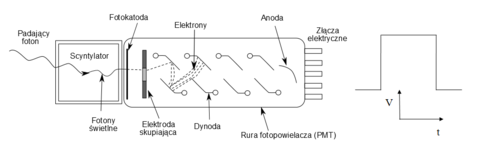
Podstawowym detektorem promieniowania γ w scyntygrafii, metodzie SPECT i PET jest detektor scyntylacyjny. Składa się in z kryształu scyntylacyjnego połączony z fotopowielaczem. Schemat takiego układu zaprezentowano na rys. 7. Zasada działania detektora scyntylacyjnego polega na zamianie energii promieniowania γ na błyski światła widzialnego (scyntylacje). Wytworzona liczba błysków scyntylacyjnych jest zbyt mała, aby można było je bezpośrednio obserwować. Do ich wzmocnienia stosuje się fotopowielacz, który jest pewnym rodzajem lampy elektronowej. Fotopowielacz składa się z następujących elementów:
- Fotokatody, która pod wpływem światła widzialnego emituje elektrony.
- Siatki elektrod, nazywanych dynodami, pomiędzy którymi istnieje pewna różnica potencjałów. Elektrony emitowane przez fotokatodę, pokonują drogę pomiędzy dynodami są przyspieszane. W trakcie zderzenia z dynodą elektrony wybijają kolejne elektrony, w efekcie czego liczba elektronów narasta. Ostatnią elektrodą w fotopowielaczu jest tzw. anoda. Elektrony uderzając w anodę powodują wytworzenie impulsu elektrycznego.
Zadaniem fotopowielacza jest zatem konwersja światła widzialnego na sygnał elektryczny oraz jego wzmocnienie.
Poniżej opisano najważniejsze fakty związane z działaniem detektora scyntylacyjnego i fotopowielacza.
Procesy zachodzące krysztale scyntylacyjnym
- Kwant promieniowania gamma oddziałuje z atomami scyntylatora w zjawiskach: Efekt Fotoelektryczny, rozproszenie Comptona oraz Kreacja Par.
- Wytworzone w tych procesach elektrony posiadają wysoką energię i powodują wytwarzanie wtórnych elektronów.
- Wytworzone elektrony pobudzają atomy scyntylatora.
- Atomy oddają nadmiar energii w postaci promieniowania E-M w zakresie widzialnym, w liczbie około 40 fotonów na każdy keV energii promieniowania gamma.
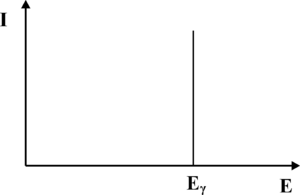
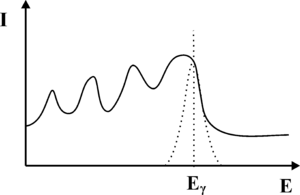
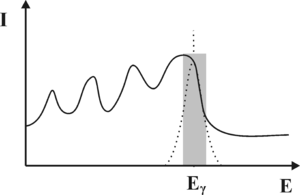
Z punktu widzenia konwersji fotonów γ na światło widzialne, najważniejszym procesem jest efekt fotoelektryczny. W wyniku tego procesu wysokoenergetyczne kwanty promieniowania γ wybijają elektrony z atomów scyntylatora. Energia wiązania elektronów z atomami scyntylatora jest niewielka w porównaniu energią fotonów γ, dlatego możemy przyjąć iż wybite elektrony przejmują w postaci energii kinetycznej cała energię fotonu. Szybko poruszające się elektrony wzbudzają atomy scyntylatora prowadząc do aktów emisji promieniowania elektromagnetycznego z zakresu widzialnego. Natężenie fotonów światła widzialnego jest proporcjonalna do energii fotonów gamma. Z kolei światło w fotopowielaczu, co zostanie omówione w dalszej części rozdziału, ulega konwersji na sygnał elektryczny, którego amplituda jest proporcjonalna do natężenia światła padającego na fotopowielacz. Podsumowując, oczekujemy, że wejściu fotopowielacza, uzyskamy impuls elektryczny, którego amplituda odpowiada energii fotonów gamma, zaś liczba impulsów otrzymywanych w jednostce czasu z fotopowielacza odpowiada natężeniu promieniowania γ padającego na scyntylator. Wykres natężenia promieniowania γ w funkcji energii nazywamy widmem. Przebieg oczekiwanego widma fotonów γ uzyskiwanych za pomocą detektora scyntylacyjnego zaprezentowano na rys. 1. Pionową linię odpowiadającą energii [math]E_\gamma[/math] fotonów gamma nazywamy fotopikiem.
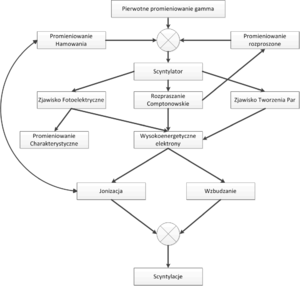
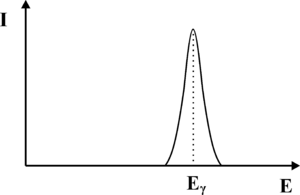
Promieniowanie elektromagnetyczne może jednak oddziaływać również z materią w procesach innych niż efekt fotoelektryczny. Fotony promieniowania γ będą w scyntylatorze ulegać rozproszeniu Comptonowskiemu oraz brać udział w procesie Kreacji Par. W wyniku zajścia efektu Comptonowskiego, powstaną wtórne fotony γ o energii niższej niż foton pierwotny. Fotony Comptonowskie z kolei mogą w wyniku procesu fotoelektrycznego wybijać elektrony, jednakże energia wybitych elektronów będzie niższa niż energia promieniowania γ. Elektrony te słabiej wzbudzą ośrodek scyntylacyjny, co doprowadzi do powstania mniejszej liczby fotonów z zakresu widzialnego. Co przełoży się na niższa amplitudę sygnału elektrycznego na wyjściu fotopowielacza. Podsumowując, fotony γ, które ulegną rozproszeniu Comptonowskiemu, będą interpretowane na wyjściu aparatury pomiarowej jako fotony γ o energii niższej niż wynikało to z rozpadu promieniotwórczego znacznika w radiofarmaceutyku. Musimy również pamiętać, iż od momentu wniknięcia fotonu γ do kryształu scyntylacyjnego, do chwili powstania upływa pewien okres czasu, w szczególności jeśli foton nie ulegnie od razu efektowi fotoelektrycznemu. Diagram niektórych oddziaływań, jakim może być ulec foton γ zanim doprowadzi do wytworzenia błysku scyntylacyjnego zaprezentowano na rys. 2. Z uwagi na skończony czas zachodzenia procesu konwersji fotonu γ na fotony widzialne, dwa kwanty promieniowania γ które wnikną w zbyt krótkich odstępach czasu do scyntylatora, będą nierozróżnialne i interpretowane jako jeden kwant o energii wyższej niż wynikałoby to z rozpadu promieniotwórczego znacznika w radiofarmaceutyku. Opisane zjawiska doprowadzą do rozmycia oczekiwanego kształtu fotopiku. Zamiast dyskretnej linii, otrzymamy krzywą o kształcie dzwonowym, której pozycja odpowiada energii fotonów γ padających na scyntylator (patrz rys. 3). Szerokość krzywej opisujemy za pomocą parametru FWHM. Problem rozmycia fotopiku możemy również wyjaśnić w oparciu o Mechanikę Kwantową. Jak wiemy nie jest możliwe wyznaczenie jednocześnie z dowolną dokładnością energii i czasu. Jeśli moment wystąpienia błysku scyntylacyjnego możemy określić z dokładnością Δt to związane będzie z tym rozmycie energii błysku ΔE. Rozmycie fotopiku nie jest jedynym problemem, który utrudnia prawidłowe określenie natężenia fotonów γ w funkcji energii. Kwant promieniowania γ wytworzony w wyniku rozpadu znacznika w radiofarmaceutyku, zanim dotrze do scyntylatora, może ulec procesom które zmienią jego energię. W niniejszych materiałach opiszemy dwa najważniejsze zjawiska, prowadzące do zmiany energii fotonów γ Pierwszym zjawiskiem jest rozpraszania Comptonowskie, które zachodzi na atomach scyntylatora. Energię rozproszonego w procesie Comptonowskim fotonu określa następujący wzór:
gdzie:
[math]E'[/math] — energia fotonu rozproszonego,
[math]E[/math] — energia fotonu padającego,
[math]c, m_e[/math] — odpowiednio prędkość światła i masa elektronu,
[math]\Theta[/math] — kąt pod jakim zostanie rozproszony foton wtórny, względem kierunku fotonu padającego.
W przypadku gdy kierunek ruchu fotonu wtórnego jest przeciwny do kierunku ruchu padającego, mówimy o rozpraszaniu wstecznym.
Kąt [math]\Theta[/math] wynosi wtedy 180 stopni, zaś energia fotonu rozproszonego wynosi:
Energia zdeponowana przez foton padający w krysztale scyntylacyjnym jest równa różnicy energii fotonu padającego i fotonu rozproszonego. W przypadku rozpraszania wstecznego jest ona równa:
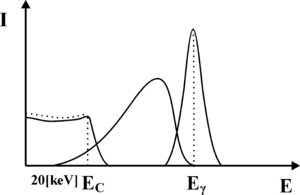
Zauważmy, iż jeśli foton ulega rozproszeniu Comptonowskiego, to może on zdeponować najwięcej energii w krysztale scyntylacyjnym właśnie w trakcie rozpraszania wstecznego. Przekaz większej energii do kryształu scyntylacyjnego w wyniku pojedynczego akty rozpraszania Comptonowskiego jest niemożliwy. Przykładowo, jeśli na do kryształu scyntylacyjnego docierają fotony γ o energi [math]E_{\gamma} = 140[/math] keV (emitowane przez Technet), to fotony wtórne powstałe w wyniku wstecznego rozpraszania Comptonowskiego będą miały energię 90 keV, zaś w krysztale zostanie zdeponowana energia 50 keV. Rozpraszanie Comptonowskie, jest zatem nie tylko odpowiedzialne za produkcję fotonów wtórnych, które prowadzą do poszerzenia fotopiku lecz także formują nową składową widma uzyskiwanego z detektora scyntylacyjnego. Składowa ta, którą określa się jako składową Comptonowską, została zaprezentowana na rysunku rys. 4. Jej charakterystyczną cechą jest gwałtowny zanik, dla energii wyższych niż pewien próg, którym jest energia zdeponowana przez fotony γ w krysztale, w trakcie wstecznego rozpraszania Comptonowskiego. Próg ten nazwano krawędzią Comptonowską. Krawędź ta w rzeczywistym widmie jest nie znacznie rozmyta, co ponownie jest związane ze statystycznym charakterem zjawisk, które prowadzą do jej utworzenia.
Kolejna składowa widma promieniowania γ uzyskiwana w detektorze scyntylacyjnym jest również związana z rozpraszaniem Comptonowskim fotonów, ale zachodzącym w organizmie pacjenta. Jej kształt będzie zależał między innymi od grubości badanego przedmiotu. W cienkim przedmiocie będą dominowały fotony, które uległy pojedynczemu rozproszeniu Comptonowskiemu, a zatem ich minimalna energia wynosi w wypadku technetu 90 keV. W praktyce jednak w pacjencie większe znaczenie mogą odegrać fotony rozproszone wielokrotnie, których energia końcowa może być znacznie niższa. Jak pamiętamy z materiałów dotyczących promieniowania rentgenowskiego, promieniowanie elektromagnetyczne o energii poniżej 10 keV jest silnie tłumione przez ciało człowieka, dlatego nie zaobserwujemy fotonów γ rozproszonych Comptonowsko o energiach poniżej tego progu. Pozostałe fotony, które uległy oddziaływaniu Comptonowskiego, będą miały energię z zakresu od około 10-20keV do maksymalnej energii, jaką dany foton może uzyskać w wyniku rozpadu promieniotwórczego. Fotony te, oddziałując ze scyntylatorem uformują składową widma zaprezentowaną na rys. 5.
Fotony emitowane z radiofarmaceutyku mogą brać udział również w innych procesach (np. ulegać rozpraszaniu Comptonowskiemu w ołowianym kolimatorze założonym na detektor) prowadząc do powstawania kolejnych składowych widma. Proces te nie będą tutaj omawiane. Należy jednak pamiętać, iż widma te mogą nakładać się na fotopik, prowadząc do jego zniekształcenia, co zaprezentowano na rysunku rys. 6.
Precyzyjne określenie natężenia i energii fotonów γ docierających do scyntylatora jest niezwykle istotne dla prawidłowego utworzenia obrazu rozkładu radiofarmaceutyku w ciele pacjenta. Natężenie kwantów promieniowania przekłada się na stężenie radiofarmaceutyku, który np. mógł ulec absorpcji przez pewien narząd co może być wskazywać na zachodzące w nim procesy chorobotwórcze. Z kolei w oparciu o energię fotonów można rozróżnić fotony, które do momentu wytworzenia błysku scyntylacyjnego nie uległy innym procesom, no. rozpraszaniu Comptonowskiemu, które mogło zmienić ich kierunek poruszania się. Problem ten zostanie jeszcze poruszony w kolejnych rozdziałach.
Procesy zachodzące w fotopowielaczu.
- Fotony światła widzialnego wytworzone w scyntylatorze docierają do katody fotopowielacz, powodując emisję z niego elektronów.
- Wprowadzony pomiędzy kolejnymi dynodami potencjał elektryczny prowadzi do przyspieszenie elektronów. Kierunek pola elektrycznego jest tak dobrany, aby elektrony kierowane były do kolejnych dynod. Elektrony w trakcie zderzenia z dynodami wybijają z nich kolejne elektrony, które ponownie są przyspieszane przez pole elektryczne.
- Ostatnią elektrodą jest anoda. Elektrony po dodarciu do niej wywołują impuls elektryczny. Impuls ten dodatkowo jest wzmacniany za pomocą wzmacniacza liniowego.
- Energia kwantu gamma przekłada się na liczbę błysków scyntylacyjnych. Z kolei od liczby błysków scyntylacyjnych zależy liczba wybitych elektronów z fotokatody, a w związku z tym również amplituda sygnału elektrycznego na wyjściu fotopowielacza.
Budowa Gamma Kamery
Okres przez powstaniem "Gamma-Kamery"
Najprostszym pomysłem na budowę aparatury do rejestracji promieniowania gamma powstałego emitowanego przez radiofarmaceutyk wprowadzony do pacjenta byłoby umieszczenie nad nim detektora scyntylacyjnego. Detektor taki jednak obejmował by swoim polem widzenia tylko niewielki obszar pacjenta, podczas gdy wiele narządów człowieka (np. płuca, układ pokarmowy, układ kostny) charakteryzuje się znacznymi rozmiarami. Problem ten można rozwiązać, umieszczając obok siebie kilka detektorów scyntylacyjnych i tego rodzaju układy były stosowane w początkach diagnostyki nuklearnej. Niestety, taki narzędzia nadal miały ograniczony zakres stosowalności i sprawdzały się w diagnostyce małych narządów (np. tarczycy). W celu zobrazowania większych narządów, detektor scyntylacyjny umieszczano na wysięgniku, który wykonywał w obrębie ciała pacjenta sekwencje pewnych ruchów (tzw. ruchów meandrujących). Detektor rejestrował emitowane z ciała ludzkiego fotony γ, które po zamianie na impuls elektryczny były kierowane do pisaka. Pozycja pisaka odpowiadała pozycji ramienia trzymającego detektor scyntylacyjny względem ciała pacjenta. Liczba punktów naznaczonych dla danej pozycji x i y odpowiadała liczbie rejestrowanych fotonów. W ten sposób uzyskiwano mapę rozkładu radiofarmaceutyku w ciele pacjenta.
Gamma-Kamera
Budowa urządzenia diagnostycznego na zasadzie łączenie ze sobą kolejnych detektorów scyntylacyjnych okazała mało optymalnym rozwiązaniem. W roku 1957 Hal Oscar Anger, wpadł na pomysł umieszczenia wielu fotopowielaczy na jednym dużym krysztale scyntylacyjnym. W ten sposób powstała gamma-kamera, nazywana również kamerą Angera. Do pełnej funkcjonalności gamma-kamera wymagała jeszcze dwóch podzespołów elektronicznych — układu wyznaczania pozycji błysków scyntylacyjnych oraz analizatora amplitudy. Bloki te zostaną omówione w kolejnych podrozdziałach. Zasadę działania gamma kamery omówimy, dokonując eksperymentu myślowego polegającego na budowie tego urządzenia od podstaw.
Kryształ scyntylacyjny i fotopowielacze
Kryształ scyntylacyjny jest jednolitym, dużym kryształem, zazwyczaj jodku sodowego aktywowanego talem — NaI(Tl) (ze względu na silna higroskopijność tego związku kryształ jest szczelnie obudowany). Średnica kryształu wynosi od około 28 cm do około 61 cm, grubość zaś dochodzi do 9,5 cm. Grubość kryształu jest jednym z parametrów decydujących o jego właściwościach detekcyjnych (od grubości kryształu zależy efektywność detekcji oraz rozdzielczość systemu). Na powierzchni kryształu scyntylacyjnego umieszczane są fotopowielacze, w liczbie do 150 sztuk. Najczęściej jednak liczba fotopowielaczy wynosi od 37 lub 53 sztuk (patrz rys. 9). Pojedynczy błysk scyntylacyjny jest rejestrowany przez wiele fotopowielaczy. Natężenie błysku scyntylacyjnego będzie malało wraz z odległością od miejsca powstania. Na podstawie rozkładu natężenia światła rejestrowanego przez fotopowielacze można wyznaczyć pozycję na płaszczyźnie gamma-kamery miejsca wystąpienia błysku. Do najważniejszych wielkości charakteryzujących kryształ scyntylacyjny należą:
- Wydajność, to jest stosunek liczby zarejestrowanych fotonów γ do liczby fotonów wpadających do kryształu scyntylacyjnego. Nie każdy foton γ spowoduje błysk scyntylacyjny, który może być zarejestrowany przez fotopowielacz. Im grubszy kryształ scyntylacyjny, tym większe jest prawdopodobieństwo wytworzenia błysku światła. Jednak grubszy kryształ powoduje również pogorszenie przestrzennej zdolności rozdzielczej gamma. Błyski scyntylacyjne zachodząc w przypadku grubego kryształu scyntylacyjnego na różnej głębokości, co utrudnia poprawne wyliczenie pozycji błysku.
- Czas odpowiedzi i czasowa zdolność rozdzielcza. Czas odpowiedzi, to czas od momentu wniknięcia fotonu γ do kryształu do wytworzenia błysku scyntylacyjnego. Determinuje on czasową zdolność rozdzielczą kryształu. Fotony γ które dotrą do do kryształu scyntylacyjnego w odstępach czasu krótszych niż czasowa zdolność rozdzielcza, nie będą zarejestrowane jako dwa oddzielne fotony.
- Energetyczna zdolność rozdzielcza jest to stosunek szerokości połówkowej (FWHM) fotopiku do amplitudy sygnału. Wielkość ta ma znaczenie przy rozróżnianiu fotonów γ pod względem ich energii. Do kryształ scyntylacyjny dociera bowiem nie tylko promieniowanie emitowane bezpośrednio z radiofarmaceutyku umieszczonego w ciele pacjenta, lecz również promieniowanie rozproszone (którego kierunek i energia zostały zmienione) oraz promieniowanie z otoczenia. Fotony γ pochodzące od tła i zjawisk rozproszeniowych można odróżnić od fotonów bezpośrednio docierających do scyntylatora m.in. na podstawie ich energii. Im lepsza jest energetyczna zdolność rozdzielcza scyntylatora, tym można dokonać lepszego rozróżnienia fotonów.
Niektóre parametry typowych materiałów scyntylacyjnych zaprezentowano w poniższej tabeli:
| Scyntylator | NaI(T) | CsF | BGO (Bi[math]_3[/math]Ge[math]_r[/math]O[math]_{12}[/math]) |
|---|---|---|---|
| Czasowa rozdzielczość (FWHM [ns]) | 1,5 | 0,4 | 7 |
| Energetyczna zdolność rozdzielcza (FWHM [%]) | 7 | 30 | 12 |
| Wydajność detekcji fotonów 511 keV [%] dla detektorów o szer 1 cm | 45 | 50 | 67 |
Przy tak uproszczonej konstrukcji układu obrazującego pojawiają się następujące problemy:
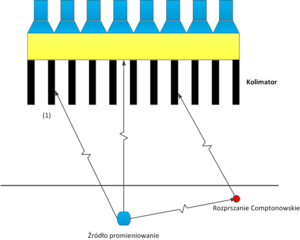
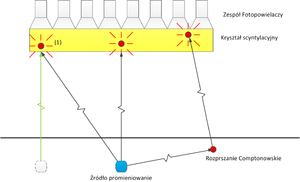
- Radiofarmaceutyk emituje promieniowanie γ izotropowo. Błysk scyntylacyjny, oznaczony na rys. 9 numerem (1), może więc być spowodowany kwantem gamma pochodzącym ze źródła oznaczonego na rys. 9 niebieskim kwadratem. Błysk scyntylacyjny numer (1) może być równie dobrze spowodowany przez kwant gamma wyemitowany ze źródła oznaczonego kwadratem białym i poruszającego się wzdłuż linii koloru zielonego.
- Kwanty γ ulegają w ciele pacjenta rozproszeniu Comptonowskiego co dodatkowo komplikuje trajektorię ich ruchu.
Kolimator
W celu uzyskania dokładnego rzutu rozkładu radiofarmaceutyku w ciele pacjenta na powierzchnie gamma-kamery stosuje się tzw. kolimatory. Kolimatory są zbudowane z ołowianej blach o średnicy takiej samej jak średnica kryształu scyntylacyjnego. Grubość kolimatora jest różna i dobierana w zależności od przeprowadzonego badania, gdyż ma wpływ na parametry uzyskiwanego obrazu. W kolimatorze wykonane są otwory, których średnica też jest zależna od rodzaju kolimatora. Zwykle otwory wywiercone są w kierunku prostopadłym do powierzchni kolimatora i mają kształt walca. W niektórych badaniach diagnostycznych otwory są pochylone w celu uzyskania powiększonego lub zmniejszonego obrazu danego narządu.
Przestrzeń pomiędzy otworami nazywamy septą. Rolą kolimatora jest filtracja promieniowania, którego kierunek znacznie odbiega od osi otworu. W przypadku otworów, które nawiercono równolegle do płaszczyzny kolimatora, tylko promieniowanie padające w przybliżeniu równolegle do osi otworu może dotrzeć do scyntylatora. Kwanty γ poruszające się winnych kierunkach będą absorbowane przez ołów wypełniający septę (przestrzeń między otworami). Sytuację taką przedstawioną rys. 11.
Parametry charakteryzujące gamma-kamerę
Spośród wielu parametrów charakteryzujących gamma-kamerę, omówimy dwa najważniejsze, to jest czułość, oraz rozdzielczość. Niestety, zwiększanie rozdzielczości przestrzennej gamma-kamery wiąże się ze zmniejszeniem jej czułości, co ma negatywny wpływ na kontrast obrazu. Problem ten omówimy poniżej, zaczynając od zdefiniowania pojęć czułości gamma — kamery oraz przypomnienia definicji rozdzielczości. Następnie omówimy jak trzy kluczowe elementy gamma-kamery, to jest kolimator, kryształ scyntylacyjny oraz fotopowielacze mają wpływ na wspomniane powyżej parametry.
- Czułość gamma-kamery.
- Czułość gamma-kamery zdefiniowana jest w następujący sposób:
- [math] sensitivity = \frac{N_o}{N_a} [/math]
- gdzie:
- [math]N_o[/math] — Liczba impulsów (fotonów) na sekundę wykorzystana przez gamma kamerę do utworzenia obrazu.
- [math]N_a[/math] — Aktywność źródła.
- W przypadku typowych gamma-kamer tylko około 3% fotonów wyemitowanych przez źródło jest wykorzystywanych do utworzenia obrazu diagnostycznego. Czułość jest bardzo ważnym parametrem, ponieważ od liczby zarejestrowanych fotonów zależy jakość uzyskanego obraz (przede wszystkim jego obraz). Na stronie [1] udostępniony jest artykuł szkoleniowy, w którym zaprezentowano obrazy diagnostyczne utworzone przy pomocy różnej liczby fotonów.
- Rozdzielczość gamma-kamery
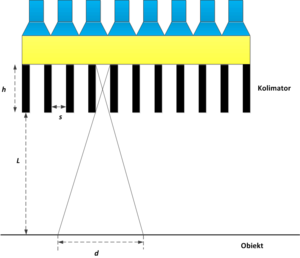
- Przypominamy, że rozdzielczość układu obrazującego to jego zdolność do zaprezentowania dwóch punktów znajdujących się w pewnej odległości od siebie, jako dwóch oddzielnych obiektów na obrazie. Na rys. 10 widzimy, że dana septa w kolimatorze przepuszcza do scyntylatora fotony pochodzące z obszaru o długości [math]d[/math]. W związku z tym, wszystkie punkty znajdujące się w obrębie tego obszaru zostaną na obrazie zaprezentowane jako jeden punkt. Parametr [math]d[/math] określa zatem rozdzielczość kolimatora. Z prostych relacji geometrycznych, uzyskamy następującą zależność parametru [math]d[/math] od głębokości h i szerokości s septy oraz odległości l kryształu scyntylacyjnego od badanego obszaru:
- [math] d = 2\frac{(l + h)s}{h} -s= 2s(1+\frac{l}{h}) -s [/math]
- Z powyższego wzoru możemy wyciągnąć następujące wnioski:
- Rozdzielczość kolimatora, co ma wpływ na rozdzielczość całej gamma-kamery, zależy od odległości kryształu scyntylacyjnego od badanego obiektu. Odległość gamma-kamery od pacjenta podlega oczywiście pewnej regulacji, jednak poszczególne narządy znajdują się w człowieku na różnej głębokości. Najwyższą rozdzielczość można uzyskać dla narządów znajdujących się tuz pod powierzchnią skóry.
- Rozdzielczość gamma-kamery można zwiększyć zmniejszając rozmiar septy oraz zwiększając jej głębokość. Jednakże zabiegi te spowodują, że do scyntylatora dotrze mniejsza ilość fotonów, skutkiem czego obniżona zostanie czułość gamma-kamery. Ponadto, zadaniem gamma-kamery jest dostarczenia obrazu uzyskanego jednocześnie z danego obszaru pacjenta. Aby pożądany obszar został objęty przez pole widzenia gamma-kamery, kolimatory o bardzo małej szerokości otworów s, powinny tych otworów zawierać jak najwięcej. Spełnienie tego warunku wymaga z kolei, aby grubości septy były jak najmniejsze. Z kolei rolą septy jest pochłanianie fotonów, które docierają z sąsiednich otwór oraz fotonów rozproszonych Comptonowsko. Cienka septa będzie pochłaniała małą liczbę fotonów, przyczyniając się do zaszumienia obrazu. Im większa jest energia fotonów emitowanych przez radiofarmaceutyk, tym septa powinna charakteryzować się większą grubością, Jak widzimy, dobór odpowiednich parametrów h oraz s jest trudny, dlatego zwykle gamma-kamera wyposażona jest w wiele kolimatorów, zmienianych przez technika, w zależności od rodzaju badania i efektu jaki chcemy uzyskać.
Fotopowielacze
Za kolimatorem w gamma-kamerze znajduje się kryształ scyntylacyjne, a dopiero później fotopowielacze, jednakże w celu lepszego omówienia kwestii rozdzielczości kryształu scyntylacyjnego, kolejność omawiania poszczególnych elementów została zmieniona. Jak pamiętamy, zadaniem pojedynczego fotopowielacza jest konwersja błysku scyntylacyjnego na sygnał elektryczny z jednoczesnym wzmocnieniem sygnału. W gamma-kamerze na krysztale scyntylacyjnym znajduje się cały zespół fotopowielaczy, którego zadaniem jest również określenie współrzędnych błysku w płaszczyźnie kolimatora. Odbywa się według bardzo prostego pomysłu. Poszczególne kolimatory znajdują się w różnych odległościach od miejsca wystąpienia błysku scyntylacyjnego, będą zatem rejestrować światło pochodzące od błysku o różnym natężeniu. Znając poszczególne pozycje fotopowielaczy oraz natężenie rejestrowanego przez nie światła, współrzędne błysku można wyznaczyć w następujący sposób:
gdzie:
[math]N[/math] — liczba fotopowielaczy,
[math]x_i, y_i[/math] — to odpowiednio, współrzędna x oraz y i-tego fotopowielacza,
[math]a_i[/math] — amplituda błysku scyntylacyjnego zarejestrowana przez i-ty fotopowielacz.
Dokładność wyznaczenia błysku scyntylacyjnego zależy oczywiście od liczby fotopowielaczy. Fotopowielacze charakteryzują się jednak relatywnie dużymi rozmiarami i nie można na krysztale scyntylacyjnym umieścić dowolnie dużo. Ponadto, liczba fotonów emitowanych w danym kierunku w trakcie błysku scyntylacyjnego podlega statystycznym fluktuacjom, które mogą być opisane rozkładem Poissona. Przykładowo, wyobraźmy sobie, iż w wyniku błysku scyntylacyjnego, który zaszedł w tej samej odległości pomiędzy dwoma fotopowielaczami, zostało wyprodukowanych 100 fotonów. Należałoby oczekiwać, iż każdy z fotopowielaczy zarejestruje po 50 fotonów. Jednakże w wyniku fluktuacji statystycznych, które są na poziomie [math]\sqrt{N}[/math], gdzie [math]N[/math] to liczba emitowanych fotonów, jeden z fotopowielaczy może zarejestrować 40 fotonów, a drugi 60. W efekcie położenie błysku scyntylacyjnego zostanie oszacowane nieprawidłowo. Celem zmniejszenia opisanego błędu, należałoby stosować radionuklidy produkujące fotony γ o wysokiej energii. Jak wiemy bowiem liczba fotonów produkowanych w trakcie błysku scyntylacyjnego zależy liniowo od energii fotonów gamma. W ten sposób względny błąd zliczeń wykazywanych przez fotopowielacze jest proporcjonalny do [math]\frac{\sqrt{N}}{N}[/math]. Detekcja fotonów γ o wyższych energiach wymaga z kolei grubszych kryształów scyntylacyjnych, co z kolei znowu negatywnie wpływa na rozdzielczość przestrzenną, co zostanie opisane w kolejnym rozdziale.
Kryształ scyntylacyjny
Foton promieniowania γ po wniknięciu w kryształ scyntylacyjny przebywa pewną drogę, zanim ulegnie oddziaływaniu z materią kryształu. Im cieńszy kryształ scyntylacyjny, tym mniejsze prawdopodobieństwo zajścia błysku scyntylacyjnego i detekcji kwantu promieniowania γ. W celu podwyższenia czułości kryształu scyntylacyjnego, należałoby zwiększyć jego grubość, jednakże to z kolei pogorszy rozdzielczość przestrzenną samego kryształu. Błyski scyntylacyjne będą mogły zachodzić na różnej głębokości, co negatywnie wpływa na określenie pozycji błysku zgodnie ze wzorem (Equation 21).
Wypadkowa rozdzielczość gamma-kamery
Wypadkowa rozdzielczość gamma-kamery jest wypadkową rozdzielczości poszczególnych jej elementów (głównie kryształu scyntylacyjnego oraz kolimatora) i wynosi:
- około 4 mm dla tkanek położnych płytko (do 2cm),
- około 10 mm dla tkanek położonych głęboko (8 cm).
Tomografia Emisyjna Pojedynczego Fotonu (ang. Single Photon Emission Tomography, SPECT)
Podobnie jak w klasycznej (planarnej) radiografii, obraz pacjenta uzyskiwany za pomocą gamma-kamery jest rzutem trójwymiarowego obiektu na płaszczyznę. Związane są z tym liczne wady tego rodzaju obrazowania, czego efektem było opracowanie na początku lat 80 tzw. Tomografii Emisyjnej Pojedynczego Fotonu (ang. Single Photon Emmision Tomography, SPECT). SPECT jest metodą obrazowania, w której na odstawie zarejestrowanych danych, zostaje zrekonstruowany obraz wybranych warstw pacjenta, wykorzystywane są przy tym dwie lub trzy gamma-kamery. Jak wiemy, rekonstrukcja obrazu wymaga dokonania rzutów obiektu na płaszczyznę z różnych kierunków. W urządzeniu SPECT gamma-kamery wykonują zatem ruch obrotowy wokół pacjenta. Przykładowe zdjęcia tomografów SPECT można zobaczyć na poniższej stronie internetowej [2].
Niestety, z rekonstrukcją obrazów w metodzie SPECT związane są pewne problemy:
- Część fotony γ zanim opuści ciało pacjenta może zostać pochłonięta.
- Natężenie wiązki kwantów γ emitowanych ze źródła umieszczone w pacjencie maleje wraz z kwadratem odległości.
- Podstawowe algorytmy rekonstrukcji obrazów wymagają dokonania rzutów obiektu z możliwie wielu kierunków. W metodzie SPECT, w której stosowane są radiofarmaceutyki kierunek emisji fotonów γ podlega pewnym fluktuacjom statystycznym i nie ma gwarancji, iż dla rzutu obiektu w danym kierunku zostanie zebrana odpowiednia ilość danych. Problem ten rozwiązuje się poprzez zastosowanie tzw. Iteracyjnych Algorytmów Rekonstrukcji obrazu.
Konsekwencje dwóch pierwszych problemów zostaną omówione w kolejnym rozdziale.
Rekonstrukcja obrazów w metodzie SPECT
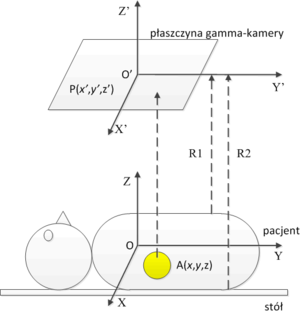
Na rys. 13 zaprezentowano układ pacjent — gamma-kamera. Z pacjentem związany jest układ współrzędnych U o środku w punkcie O, z kolei z gamma-kamerą związany jest układ U' z środkiem w punkcie O' . Odległość pomiędzy środkami układu współrzędnych wynosi R. Pacjentowi podano radiofarmaceutyk (zaznaczony na rys. 13 kolorem żółtym), który został wychwycony przez płuca. Rozkład przestrzenny radiofarmaceutyku w pacjencie opisuje funkcja A(x,y,z). Odległość od mostka pacjenta do płaszczyzny gamma-kamery wynosi [math]R_1[/math], zaś odległość od pleców do płaszczyzny gamma-kamery wynosi [math]R_2[/math]. Zakładamy, iż kolimator (nie zaprezentowany na rysunku) odrzuci każdy kwant promieniowania γ który nie pada na kolimator pod kątem prostym. Przy powyższych założeniach, rozkład błysków scyntylacyjnych, odzwierciedlających rozkład radiofarmaceutyku w następujący sposób. W przypadku braku zaniku natężenia promieniowania wraz z odległością, rozkład natężenia błysków scyntylacyjnych byłby rzutem prostokątnym rozkładu radiofarmaceutyku na płaszczyznę gamma-kamery, z uwzględnieniem faktu, iż radiofarmaceutyk znajduje się na różnej głębokości w pacjencie:
Wzór (Equation 22) opisuje nic innego jak Transformatę Radona rozkładu raiofarmaceutyku. Uwzględniając zanik natężenie promieniowania γ wraz z odległością, wzór (Equation 22) przyjmie postać:
Niestety, kwant promieniowania γ zanim opuści organizm człowieka, może zostać pochłonięty na skutek różnych procesów, co opisuje liniowy współczynnik osłabienia promieniowa [math]\mu(x,y,z)[/math]. Uwzględniając pochłanianie, dostajemy:
Wzór (Equation 22) nie reprezentuje już Transformaty Radona rozkładu raiofarmaceutyku w pacjencie. Główny trudność stanowi jednak brak znajomości rozkładu współczynnika [math]\mu(x,y,z)[/math]. Istnieją różne podejścia do rozwiązania tego problemu:
- zakłada się brak osłabienia promieniowania γ ([math]\mu(x,y,z)[/math] = 0),
- zakłada się stały rozkład wartości osłabienia promieniowania ([math]\mu(x,y,z)[/math] = const),
- aproksymuje się [math]\mu(x,y,z)[/math], przy pomocy innych metod, np. CT.
Ostatnie rozwiązanie nazywane jest korejestracją SPECT-CT. Urządzenie do korejestracji składają się z dwóch połączonych ze sobą skanerów CT i SPECT.
Radionuklidy stosowane w badaniach planarnych oraz metodzie SPECT
Radionuklidy stosowane w badaniach, w których wykorzystywana jest gamma-kamera, powinny spełniać następujące wymagania:
- Emitować kwanty gamma bez udziału innych przemian promieniotwórczych (alfa/beta).
- Charakteryzować się odpowiednio długim czasem połowicznego rozpadu, umożliwiającym przeprowadzenie badania diagnostycznego.
- Emitować kwanty gamma o energii:
- wystarczająco dużej, aby fotony przenikały przez ciało ludzkie (min. 20 keV),
- wystarczająco niskiej, aby w wyniku oddziaływania fotonów z materią nie dochodziło do wtórnych procesów (poniżej 511 keV).
- wystarczająco dużej, aby fotony przenikały przez ciało ludzkie (min. 20 keV),
Wszystkie te wymagania spełnia izotop Technetu — [math]^{99}\mathrm{Tc}[/math]. Charakteryzuje się on energią emisji kwantów promieniowania γ wynoszącą 140 keV oraz czasem połowicznego rozpadu wynoszącym [math]T_{\frac{1}{2}}=6[/math] godzin. Emisji fotonów promieniowania elektromagnetycznego nie towarzyszą inne przemiany promieniotwórcze. Właściwości te czynią Technet wręcz idealnym radionuklidem w zastosowaniach diagnostyki nuklearnej z wykorzystaniem gamma-kamery.
Procesu uzyskiwania Technetu jest następujący. Przemiany zachodzące w reaktorze jądrowym są źródłem radioizotopu [math]^{99}\mathrm{Mo}[/math] (Molibden).
Izotop ten jest umieszczany w specjalnie zabezpieczonym pojemniku, nazywanym generatorem radionuklidu. Generator dostarczany jest do odbiorcy.
Izotop Molibdenu ulega przemianie [math]\beta^-[/math] z czasem połowicznego rozpadu [math]T_{\frac{1}{2}}=65,98 [/math] godzin (2,75 dnia).
Produktem przemiany jest w 87,5 % tzw. metastabilny izotop technetu [math]^{99}\mathrm{Tcm}[/math], znajdujący się w stanie wzbudzonym, zaś w 12,5 % "zwykły" izotop technetu. Technet metastabilny ulega przemianie gamma, z czasem połowicznego rozpadu wynoszącym [math]T_{\frac{1}{2}}=6[/math] godzin. W celu uzyskania użytecznego w diagnostyce nuklearnej Technetu metastabilnego jest on wypłukiwany przez technika z generatora i poddawany dalej kolejnym obróbkom chemicznym. Jak widzimy, Technet charakteryzuje się nie tylko dobrymi właściwościami fizycznymi na potrzeby obrazowania nuklearnego, lecz również jest względnie łatwy w produkcji.
Inne radioizotopy stosowane w obrazowaniu nuklearnym to:
- Jod-123 ([math]^{131}[/math]J), o okresie połowicznego rozpadu [math]T_{\frac{1}{2}}=13[/math] dni i energii emitowanych kwantów γ równej 159 keV,
- Jod-131 ([math]^{131}[/math]J), o okresie połowicznego rozpadu [math]T_{\frac{1}{2}}=8[/math] dni i energii emitowanych kwantów γ równej 159 keV,
- Ind-111 ([math]^{131}[/math]In), o okresie połowicznego rozpadu [math]T_{\frac{1}{2}}=67[/math] godzin i energii emitowanych kwantów γ równej 245 keV.
Rola gamma-kamery w diagnostyce nuklearnej
Metody obrazowanie oparte na gamma-kamerze charakteryzują się pewnymi wadami. Do najpoważniejszych należą:
- relatywnie niska rozdzielczość przestrzenna w porównaniu z innymi metodami (przykładowo w badaniach Rentgenowskich można uzyskać rozdzielczość na poziomie 0,3 mm, podczas gdy gamma-kamera daje rozdzielczość o rząd wielkości gorszą),
- zależność rozdzielczości od głębokości obrazowanych tkanek.
Co czyni zatem gamma-kamerę wartościowym narzędziem diagnostycznym? Należy sobie uświadomić, iż wiele chorób (zwłaszcza nowotworowych) może nie prowadzić do zmian w budowie anatomicznej narządów. W związku z tym zmiany te mogą być bardzo trudno zauważalne na obrazach prezentujących strukturę tkanek. Tymczasem główna idea badania z wykorzystanie gamma-kamery polega na lokalizacji miejsc gromadzenia się radiofarmaceutyku, który (jak przypominamy) składa się z radioizotopu oraz substancji wchłanianej wybiórczo przez chore tkanki. Dzięki temu scyntygrafia czy metoda SPECT stała się ważnym narzędziem w diagnostyce nowotworów oraz ich przerzutów. Ponadto, pewne choroby mogą prowadzić do dysfunkcji narządów bez wyraźnych zmian w ich budowie anatomicznej. Metody, taka jak SPECT, wykorzystywane są w badaniach perfuzyjnych (czyli badaniach przepływu przez tkanki czy narządy określonych płynów). Takie parametry, jak tempo dotarcia raiofarmaceutyku do danego narządu, szybkość jego usunięcia, ilość raiofarmaceutyku która przepłynęła przez narząd, są wskazaniem do właściwego lub nieprawidłowego działania narządu. Jednym z rodzajów badaniach perfuzyjnych, w których wykorzystuje się metody oparte na gamma-kamerze, to diagnostyka udarów mózgu (zarówno krwotocznych jak i niedokrwiennych).
Pozytonowa Emisyjna Tomografia Komputerowa (ang. Positron Emission Tomography, PET)
Podobnie jak w przypadku Scyntygrafii czy metodzie SPECT, w Pozytonowej Emisyjnej Tomografii Komputerowej stosowane są radiofarmaceutyki. W tym przypadku jednak, radioizotopem zastosowanym jako znacznik nie jest emiter promieniowania γ lecz izotop ulegający przemianie [math]\beta^+[/math]. Ma to poważne duże konsekwencje w procesie uzyskiwania obrazu oraz budowie samego skanera.
Podstawy działania metody PET
W trakcie rozpadu [math]\beta^+[/math] emitowany jest pozyton, czyli cząstka o tej samej masie co elektron, ale o przeciwnym (dodatnim) ładunku. Cząstka ta w wyniku rozpadu uzyskuje pewną energię, którą wytraca w oddziaływaniach z otoczeniem. Po zwolnieniu do prędkości termicznych, pozyton anihiluje z elektronem znajdującym się w otoczeniu. W wyniku anihilacji powstają (w zdecydowanej ilości przypadków) dwa fotony γ, które w układzie środka masy rozbiegają się w przeciwnych kierunkach. W układzie laboratoryjnym istnieją mierzalne odstępstwa od przeciwnego kierunku ruchu kwantów γ, jednak zwykle są one pomijane. Fotony po dotarciu do detektorów promieniowania są rejestrowane. Do tworzenia obrazu wykorzystywane są te pary kwantów γ, które jednocześnie dotarły do detektorów. Innymi słowy, w metodzie PET detekcji podlegają koincydencje czasowe dotarcie kwantów γ do detektorów. Poniżej wypisano przemiany fizyczne prowadzące do emisji dwóch fotonów γ.
- Radionuklid w radiofarmaceutyku ulega rozpadowi [math]\beta^+[/math]
W trakcie przemiany, pozyton uzyskuje pewną energię kinetyczną, po wytraceniu której, zwalnia do prędkości termicznych, a następnie anihiluje z przypadkowym elektronem:
Fotony rozchodzą się w przeciwnych kierunkach.
Najprostszy sposób uzyskiwania obrazu w metodzie PET (nierealizowany w praktyce) można przeprowadzić następująco. Zgodnie z założeniem, fotony emitowane w trakcie anihilacji poruszają się w układzie laboratoryjnym w przeciwnych kierunkach. Łącząc za pomocą prostej detektory, które zarejestrowały jednocześnie dotarcie do nich fotonów γ uzyskujemy informacje, iż na tej prostej nastąpił akt anihilacji, a zatem gdzieś w pobliżu nastąpił rozpad [math]\beta^+[/math]. Prostą łączącą detektory, które zarejestrowały koincydencję czasową dotarcie dwóch fotonów γ nazywamy linią LOR (ang. Line of Response). Nakładając wiele linii LOR na siebie, możemy uzyskać rozkład raiofarmaceutyku w badanym obszarze pacjenta.
Rozdzielczość metody PET
Naturalnym ograniczeniem rozdzielczości metody PET jest droga, jaką przebywa pozyton emitowany po przemianie [math]\Beta^+[/math] zanim nie wytraci energii kinetycznej i nie ulegnie anihilacji. Przykładowo, pozytony emitowane w rozpadzie [math]\Beta^+[/math] [math]^68[/math]Ga uzyskują maksymalną, początkową energię kinetyczną równą 1,90 MeV. W ośrodku materialnym takim jak woda, 50% pozytonów o powyższej energii początkowej, zostanie wyhamowanych w kuli o promieniu 1,6 mm, zaś 90% pozytonów zatrzyma się w kuli o promieniu 3,7 mm.
Radionuklidy stosowane w metodzie PET
Wymagania stawiane izotopom promieniotwórczym stosowanym w Pozytonowej Tomografii emisyjnej są następujące:
- Izotop musi oczywiście ulegać przemianie [math]\beta^+[/math],
- Energia pozytonów emitowanych przy rozpadzie, powinna być jak najmniejsza.
Charakterystyczną cechą radioizotopów ulegających przemianie [math]\beta^+[/math] jest ich bardzo krótki okres połowicznego rozpadu, który w wielu przypadkach uniemożliwia ich praktyczne zastosowanie w diagnostyce PET. Tabela … zawiera przykłady izotopów ulegających przemianie [math]\beta^+[/math].
| Radionuklid | Okres połowicznego rozpadu [math]T_{\frac{1}{2}}[/math] [minuty] | Maksymalne energia pozytonu [keV] | Metoda otrzymywania |
|---|---|---|---|
| [math]^{11}\mathrm C[/math] | 20,4 | 961 | Cyklotron |
| [math]^{11}\mathrm O[/math] | 2,04 | 1190 | Cyklotron |
| [math]^{13}\mathrm N[/math] | 10 | 961 | Cyklotron |
| [math]^{18}\mathrm F[/math] | 109,8 | 635 | Cyklotron |
| [math]^{38}\mathrm K[/math] | 7,64 | 2680 | Cyklotron |
| [math]^{62}\mathrm{Zn}[/math] | 138 | 660 | |
| [math]^{11}\mathrm{Ga}[/math] | 68,4 | 1900 | Generator |
| [math]^{82}\mathrm{Rb}[/math] | 1,27 | 3400 | Generator |
| [math]^{122}\mathrm I[/math] | 3,60 | 3210 |
Jak widzimy, radionuklidem o stosunkowo długim okresie połowicznego rozpadu oraz niskiej energii emitowanych pozytonów jest izotop fluoru. Jest on najczęściej stosowanym znacznikiem w radiofarmaceutykach. Dołączony do glukozy (nośnika) tworzy radiofarmaceutyk fluorodeoksyglukozę (FDA). Niestety, problem stanowi praktyczne otrzymywanie izotopu [math]^{18}F[/math]. Radionuklid ten można otrzymać w cyklotronach w wyniku bombardowania przyspieszanymi protonami tarczy zawierającej tlen:
Konstrukcja Tomografu PET
Zdjęcia tomografów PET, schematy ich budowy jak i uzyskiwane za ich pomocą obrazy można zobaczyć w na stronie w Wikipedii. Skaner PET składa się z bardzo wielu detektorów scyntylacyjnych ułożonych na obwodzie pierścienia w środku którego znajduje się badana osoba. Zwykle tomograf posiada kilka rzędów takich pierścieni. O ile kryształy scyntylacyjne mogę bardzo małe rozmiary, to fotopowielacze charakteryzują się relatywnie dużymi średnicami. W celu umieszczenia na obwodzie jak największej liczby detektorów stosuje się następujące rozwiązanie. Fotopowielacze łączone są w bloki (np. po 4 sztuki) i umieszczane na jednym krysztale scyntylacyjnym. W celu zwiększenia precyzji określenia błysku scyntylacyjnego, w krysztale wykonywane są nacięcia o odpowiednio dobranej głębokości, które zostają wypełnione materiałem odbijającym światło. Fala elektromagnetyczna emitowana w błysku scyntylacyjnym odbija się na wykonanych nacięciach, co ogranicza jego transmisję w dowolnych kierunkach. Liczba opisanych detektorów umieszczonych na obwodzie pierścienia wynosi od 100 do około 1000 sztuk, zaś w jednym skanerze PET zainstalowanych jest od 16 do 32 pierścieni.
Wady i zalety PET.
- Podstawową wadą metody PET jest trudność w uzyskiwaniu radionuklidów ulegających przemianie [math]\beta^+[/math]. Najkorzystniejszy pod względem długości okresu połowicznego rozpadu oraz energii radionuklid — [math]^{18}\mathrm{F}[/math] jest otrzymywany w cyklotronie. W związku z tym, w pobliżu ośrodka klinicznego musi znajdować się cyklotron.
- W porównaniu z metodą SPECT, rozdzielczość w metodzie PET nie zależy od głębokości badanej tkanki.
- Diagnostyka PET nie wymaga mechanicznego kolimatora, który występuje w metodzie PET. Zadaniem kolimatora w SPECT była selekcja odpowiednio padających na kryształ scyntylacyjny fotonów [math]\gamma[/math]. Kolimator ren jednak uniemożliwiał jednoczesne dobranie dowolnie dużej czułości i rozdzielczości gamma kamery. W przypadku PET, kolimacja jest procesem fizycznym — rejestracji podlegają koincydencje czasowe detekcji pary dwóch fotonów [math]\gamma[/math]. W ten sposób do rekonstrukcji obrazu wykorzystywane są głównie fotony, które powstały w wyniku anihilacji (aczkolwiek istnieje niezerowe prawdopodobieństwo dotarcia w tym samym czasie dwóch przypadkowych fotonów).