TI/Programowanie dla Fizyków Medycznych/Array2D: Różnice pomiędzy wersjami
(Utworzono nową stronę "=== Gra w zycie Conwaya === <source lang="python"> import numpy as np import pylab as py py.ion() a=np.zeros((100,100)) def ile_sasiadow(x,y,macierz): return np.su...") |
|||
| (Nie pokazano 4 pośrednich wersji utworzonych przez tego samego użytkownika) | |||
| Linia 1: | Linia 1: | ||
| − | === | + | ==Ćwiczenia z przetwarzania tablic 2D== |
| + | ===Wyświetlanie tablic 2D=== | ||
| + | Jak wstęp do przetwarzania obrazów w pythonie przećwiczmy podstawowe operacje na dwuwymiarowych tablicach numpy w postaci których będziemy takie obrazy przechowywać. Zacznijmy od zdefiniowania przykładowej tablicy która będzie reprezentować obrazek. | ||
| + | <source lang="python"> | ||
| + | import numpy as np | ||
| + | import pylab as py | ||
| + | |||
| + | a=np.zeros((100,100),dtype=np.bool) | ||
| + | a[30:50,30:50]=True | ||
| + | a[50:70,50:70]=True | ||
| + | </source> | ||
| + | Stworzyliśmy w ten sposób tablice 100 na 100 z wpisanymi wartościami False oraz w środku dwa kwadraty o boku 20 z wartościami True. Już tak stworzoną tablicę możemy wyświetlić za pomocą pylaba. | ||
| + | <source lang="python"> | ||
| + | py.imshow(a) | ||
| + | py.show() | ||
| + | </source> | ||
| + | |||
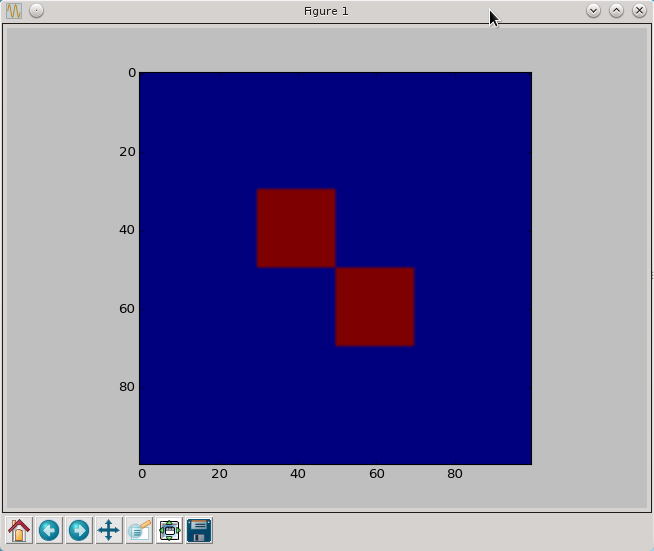
| + | [[Plik:pil1.png]] | ||
| + | |||
| + | Nie do końca możen było się spodziewać, że pylab wyświetli wartości False w kolorze granatowym a wartości True w kolorze bordowym. Za przyporządkowanie kolorów określonym wartościom odpowiada tzw. mapa kolorów, którą podajemy jako parametr w poleceniu imshow. Aby uzyskać bardziej intuicyjną skalę szarości należy wywołać polecenie następująco. | ||
| + | <source lang="python"> | ||
| + | py.imshow(a,cmap = py.cm.gray) | ||
| + | py.show() | ||
| + | </source> | ||
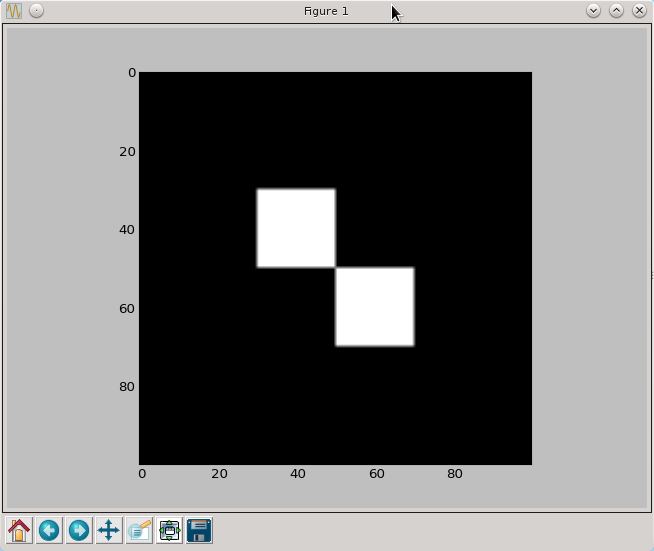
| + | [[Plik:pil2.png]] | ||
| + | |||
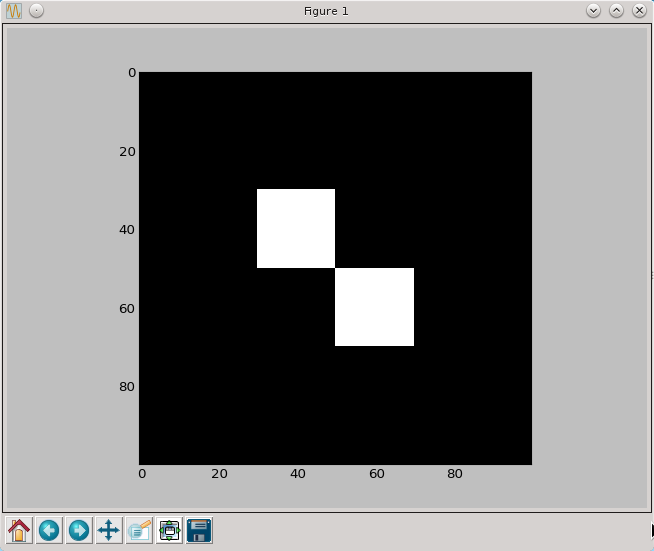
| + | Teraz kolory (a raczej ich brak) są takie jakich można było się spodziewać. Zaskakujące jest za to rozmycie brzegów kwadratów. Obrazek wyświetlany jest w większych rozmiarach niż jego domyślne 100 na 100 pixeli. Pylab aby wyświetlić go w wyższej rozdzielczości musi zwiększyć jego rozmiary. Rozciągając obrazek można w różny sposób przypisywać wartości pixelom, których nie było w pierwotnym obrazku. Proces ten nazywamy interpolacją i aby uzyskać "ostre" krawędzie należy znów użyć odpowiedniej opcji metody imshow. | ||
| + | <source lang="python"> | ||
| + | py.imshow(a,cmap = py.cm.gray, interpolation = 'nearest') | ||
| + | py.show() | ||
| + | </source> | ||
| + | |||
| + | [[Plik:pil3.png]] | ||
| + | |||
| + | === Gra w życie Conwaya === | ||
| + | W ramach ćwiczeń zaprogramujmy klasyczny automat komórkowy zwany gra w życie Conwaya. | ||
| + | W naszej wersji gra toczy się na skończonej planszy o wymiarach 100 na 100 podzielonej na kwadratowe komórki. Każda komórka (poza brzegowymi) ma ośmiu sąsiadów, czyli komórki przylegające do niej bokami i rogami. Każda komórka może znajdować się w jednym z dwóch stanów: może być albo "żywa" (stanowi przypisujemy wartość 1), albo "martwa" (wartość 0). Stan wszystkich komórek w pewnej jednostce czasu jest używany do obliczenia stanu wszystkich komórek w następnej jednostce. Po obliczeniu wszystkie komórki zmieniają swój stan jednocześnie. Stan komórki zależy tylko od liczby jej żywych sąsiadów w następujący sposób | ||
| + | *Martwa komórka, która ma dokładnie 3 żywych sąsiadów, staje się żywa w następnej jednostce czasu (rodzi się) | ||
| + | *Żywa komórka z 2 albo 3 żywymi sąsiadami pozostaje żywa, przy innej liczbie sąsiadów umiera | ||
| + | |||
| + | Zacznijmy od zdefiniowania planszy gry | ||
<source lang="python"> | <source lang="python"> | ||
import numpy as np | import numpy as np | ||
import pylab as py | import pylab as py | ||
| − | + | ||
a=np.zeros((100,100)) | a=np.zeros((100,100)) | ||
| + | </source> | ||
| + | Kluczową i najtrudniejszą funkcją jest funkcja zliczająca liczbę sąsiadów danej komórki. Problematyczne jest tutaj uwzględnienie przypadku komórek znajdujących się na rogach, które mają po trzech sąsiadów, oraz komórek brzegowych mających po 5 sąsiadów. Przykładowe rozwiązanie wygląda następująco. | ||
| + | <source lang="python"> | ||
def ile_sasiadow(x,y,macierz): | def ile_sasiadow(x,y,macierz): | ||
return np.sum(macierz[max(0,x-1):min(macierz.shape[0],x+2),max(0,y-1):min(macierz.shape[1],y+2)].flatten())-macierz[x,y] | return np.sum(macierz[max(0,x-1):min(macierz.shape[0],x+2),max(0,y-1):min(macierz.shape[1],y+2)].flatten())-macierz[x,y] | ||
| − | + | </source> | |
| + | Z tak przygotowaną funkcją ile_sasiadow możemy zdefiniować funkcję określającą logikę gry w życie. | ||
| + | <source lang="python"> | ||
def nowy_stan_komorki(x,y,macierz): | def nowy_stan_komorki(x,y,macierz): | ||
sasiadow=ile_sasiadow(x,y,macierz) | sasiadow=ile_sasiadow(x,y,macierz) | ||
| Linia 14: | Linia 59: | ||
if sasiadow==2 and macierz[x,y]==1: return 1 | if sasiadow==2 and macierz[x,y]==1: return 1 | ||
return 0 | return 0 | ||
| − | + | </source> | |
| + | Możemy teraz zdefiniować nowy stan całej planszy. | ||
| + | <source lang="python"> | ||
def krok(macierz): | def krok(macierz): | ||
wynik=macierz.copy() | wynik=macierz.copy() | ||
| − | for x in | + | for x,y in np.ndindex(wynik.shape): |
| − | + | wynik[x,y]=nowy_stan_komorki(x,y,macierz) | |
| − | |||
return wynik | return wynik | ||
| − | + | </source> | |
| + | Jak warunku początkowego możemy użyć tzw. lokomotywy. | ||
| + | <source lang="python"> | ||
lokomotywa=np.array([[1,1,1,0,1],[1,0,0,0,0],[0,0,0,1,1],[0,1,1,0,1],[1,0,1,0,1]]) | lokomotywa=np.array([[1,1,1,0,1],[1,0,0,0,0],[0,0,0,1,1],[0,1,1,0,1],[1,0,1,0,1]]) | ||
| − | |||
a[45:50,45:50]=lokomotywa | a[45:50,45:50]=lokomotywa | ||
| − | + | </source> | |
| + | W pylabie istnieje prosty sposób na wyświetlenie animacji poprzez odświeżanie już wyświetlonego obrazka. | ||
| + | <source lang="python"> | ||
| + | py.ion() | ||
for n in range(1000): | for n in range(1000): | ||
py.imshow(a, cmap='Greys', interpolation='nearest') | py.imshow(a, cmap='Greys', interpolation='nearest') | ||
| Linia 32: | Linia 82: | ||
</source> | </source> | ||
| + | |||
| + | [["Programowanie dla Fizyków Medycznych"]] | ||
Aktualna wersja na dzień 20:11, 8 cze 2015
Ćwiczenia z przetwarzania tablic 2D
Wyświetlanie tablic 2D
Jak wstęp do przetwarzania obrazów w pythonie przećwiczmy podstawowe operacje na dwuwymiarowych tablicach numpy w postaci których będziemy takie obrazy przechowywać. Zacznijmy od zdefiniowania przykładowej tablicy która będzie reprezentować obrazek.
import numpy as np
import pylab as py
a=np.zeros((100,100),dtype=np.bool)
a[30:50,30:50]=True
a[50:70,50:70]=True
Stworzyliśmy w ten sposób tablice 100 na 100 z wpisanymi wartościami False oraz w środku dwa kwadraty o boku 20 z wartościami True. Już tak stworzoną tablicę możemy wyświetlić za pomocą pylaba.
py.imshow(a)
py.show()
Nie do końca możen było się spodziewać, że pylab wyświetli wartości False w kolorze granatowym a wartości True w kolorze bordowym. Za przyporządkowanie kolorów określonym wartościom odpowiada tzw. mapa kolorów, którą podajemy jako parametr w poleceniu imshow. Aby uzyskać bardziej intuicyjną skalę szarości należy wywołać polecenie następująco.
py.imshow(a,cmap = py.cm.gray)
py.show()
Teraz kolory (a raczej ich brak) są takie jakich można było się spodziewać. Zaskakujące jest za to rozmycie brzegów kwadratów. Obrazek wyświetlany jest w większych rozmiarach niż jego domyślne 100 na 100 pixeli. Pylab aby wyświetlić go w wyższej rozdzielczości musi zwiększyć jego rozmiary. Rozciągając obrazek można w różny sposób przypisywać wartości pixelom, których nie było w pierwotnym obrazku. Proces ten nazywamy interpolacją i aby uzyskać "ostre" krawędzie należy znów użyć odpowiedniej opcji metody imshow.
py.imshow(a,cmap = py.cm.gray, interpolation = 'nearest')
py.show()
Gra w życie Conwaya
W ramach ćwiczeń zaprogramujmy klasyczny automat komórkowy zwany gra w życie Conwaya. W naszej wersji gra toczy się na skończonej planszy o wymiarach 100 na 100 podzielonej na kwadratowe komórki. Każda komórka (poza brzegowymi) ma ośmiu sąsiadów, czyli komórki przylegające do niej bokami i rogami. Każda komórka może znajdować się w jednym z dwóch stanów: może być albo "żywa" (stanowi przypisujemy wartość 1), albo "martwa" (wartość 0). Stan wszystkich komórek w pewnej jednostce czasu jest używany do obliczenia stanu wszystkich komórek w następnej jednostce. Po obliczeniu wszystkie komórki zmieniają swój stan jednocześnie. Stan komórki zależy tylko od liczby jej żywych sąsiadów w następujący sposób
- Martwa komórka, która ma dokładnie 3 żywych sąsiadów, staje się żywa w następnej jednostce czasu (rodzi się)
- Żywa komórka z 2 albo 3 żywymi sąsiadami pozostaje żywa, przy innej liczbie sąsiadów umiera
Zacznijmy od zdefiniowania planszy gry
import numpy as np
import pylab as py
a=np.zeros((100,100))
Kluczową i najtrudniejszą funkcją jest funkcja zliczająca liczbę sąsiadów danej komórki. Problematyczne jest tutaj uwzględnienie przypadku komórek znajdujących się na rogach, które mają po trzech sąsiadów, oraz komórek brzegowych mających po 5 sąsiadów. Przykładowe rozwiązanie wygląda następująco.
def ile_sasiadow(x,y,macierz):
return np.sum(macierz[max(0,x-1):min(macierz.shape[0],x+2),max(0,y-1):min(macierz.shape[1],y+2)].flatten())-macierz[x,y]
Z tak przygotowaną funkcją ile_sasiadow możemy zdefiniować funkcję określającą logikę gry w życie.
def nowy_stan_komorki(x,y,macierz):
sasiadow=ile_sasiadow(x,y,macierz)
if sasiadow==3: return 1
if sasiadow==2 and macierz[x,y]==1: return 1
return 0
Możemy teraz zdefiniować nowy stan całej planszy.
def krok(macierz):
wynik=macierz.copy()
for x,y in np.ndindex(wynik.shape):
wynik[x,y]=nowy_stan_komorki(x,y,macierz)
return wynik
Jak warunku początkowego możemy użyć tzw. lokomotywy.
lokomotywa=np.array([[1,1,1,0,1],[1,0,0,0,0],[0,0,0,1,1],[0,1,1,0,1],[1,0,1,0,1]])
a[45:50,45:50]=lokomotywa
W pylabie istnieje prosty sposób na wyświetlenie animacji poprzez odświeżanie już wyświetlonego obrazka.
py.ion()
for n in range(1000):
py.imshow(a, cmap='Greys', interpolation='nearest')
a=krok(a)
py.draw()