TI/Programowanie dla Fizyków Medycznych/Morfologia matematyczna: Różnice pomiędzy wersjami
| (Nie pokazano 1 pośredniej wersji utworzonej przez tego samego użytkownika) | |||
| Linia 1: | Linia 1: | ||
==Morfologia matematyczna== | ==Morfologia matematyczna== | ||
| − | Morfologia matematyczna to bardzo przydatna metoda przetwarzania obrazów binarnych (czarno-białych), pozwalająca na analizę i "upraszczanie" obserwowanych kształtów. W szczególności można ją zastosować do obrazów medycznych przetworzonych | + | Morfologia matematyczna to bardzo przydatna metoda przetwarzania obrazów binarnych (czarno-białych), pozwalająca na analizę i "upraszczanie" obserwowanych kształtów. W szczególności można ją zastosować do obrazów medycznych przetworzonych przez progowanie. Metody morfologii matematycznej pozwalają także na uspójnienie otrzymanego obrazu nie zmieniając jego rozmiarów zewnętrznych co może być bardzo przydatne przy dokonywaniu pomiarów w oparciu o cyfrowy obraz medyczny. Dla osób zainteresowanych bardziej formalną definicją poszczególnych operacji polecam bardzo szeroką literaturę dostępną w internecie. Tutaj przedstawimy definicję pozwalającą na łatwiejsze zrozumienie istoty działania poszczególnych operacji. Operacje morfologii matematycznej opierają się na tak zwanym elemencie strukturalnym, który my w uproszczeniu nazywać będziemy pędzlem (brush). Zacznijmy od zdefiniowania naszego obrazu roboczego i przykładowego pędzla. |
<source lang="python"> | <source lang="python"> | ||
import numpy as np | import numpy as np | ||
| Linia 28: | Linia 28: | ||
===Dylacja=== | ===Dylacja=== | ||
| − | Pierwszą operacją którą omówimy jest dylacja. Nasz obraz w chwili obecnej składa się z tła zer (w kolorze czarnym) i dwóch kwadratów z jedynek (w kolorze białym). Wyobraźmy sobie, że nasz pędzel służy do malowania po obrazku. Jeżeli w jakimś miejscu przyłożymy środek pędzla, to wszystkie pixele, na których znajdą się jedynki w pędzlu zmienią swoją wartość na jeden. Operacja dylacji to przyłożenie środka pędzla do wszystkich komórek, których początkowa wartość to jeden. Równoważna jest także inna definicja. Przykładamy środek pędzla po kolei do wszystkich pixeli. Tworzymy listę wartości pixeli obrazu które w danym ułożeniu pędzla odpowiadając wartościom 1 na pędzlu. Do pixela w którym znajduje się środek pędzla przypisujemy wartość będącą '''maksimum''' z tej list. Implementacja drugiej z tych definicji znajduje się poniżej. | + | Pierwszą operacją którą omówimy jest dylacja. Nasz obraz w chwili obecnej składa się z tła zer (w kolorze czarnym) i dwóch kwadratów z jedynek (w kolorze białym). Wyobraźmy sobie, że nasz pędzel służy do malowania po obrazku. Jeżeli w jakimś miejscu przyłożymy środek pędzla, to wszystkie pixele, na których znajdą się jedynki w pędzlu zmienią swoją wartość na jeden. Operacja dylacji to przyłożenie środka pędzla do wszystkich komórek, których początkowa wartość to jeden. Równoważna jest także inna definicja. Przykładamy środek pędzla po kolei do wszystkich pixeli. Tworzymy listę wartości pixeli obrazu, które w danym ułożeniu pędzla odpowiadając wartościom 1 na pędzlu. Do pixela w którym znajduje się środek pędzla przypisujemy wartość będącą '''maksimum''' z tej list. Implementacja drugiej z tych definicji znajduje się poniżej. |
<source lang="python"> | <source lang="python"> | ||
def dylacja(fig,brush=np.array([[0,1,0],[1,1,1],[0,1,0]],dtype=np.bool)): | def dylacja(fig,brush=np.array([[0,1,0],[1,1,1],[0,1,0]],dtype=np.bool)): | ||
| Linia 45: | Linia 45: | ||
W efekcie dwa kwadraty powiększyły się i zaokrągliły im się rogi. | W efekcie dwa kwadraty powiększyły się i zaokrągliły im się rogi. | ||
| + | |||
===Erozja=== | ===Erozja=== | ||
Drugą operacją morfologii matematycznej jest erozja. Operacja jest analogiczna, z tą zmianą, że teraz nasz pędzel maluje na czarno i przesuwamy go po czarnych pixelach. Przy alternatywnej definicji przykładamy środek pędzla po kolei do wszystkich pixeli. Tworzymy listę wartości pixeli obrazu które w danym ułożeniu pędzla odpowiadając wartościom 1 na pędzlu. Do pixela w którym znajduje się środek pędzla przypisujemy wartość będącą '''minimum''' z tej list. Implementacja drugiej z tych definicji znajduje się poniżej. | Drugą operacją morfologii matematycznej jest erozja. Operacja jest analogiczna, z tą zmianą, że teraz nasz pędzel maluje na czarno i przesuwamy go po czarnych pixelach. Przy alternatywnej definicji przykładamy środek pędzla po kolei do wszystkich pixeli. Tworzymy listę wartości pixeli obrazu które w danym ułożeniu pędzla odpowiadając wartościom 1 na pędzlu. Do pixela w którym znajduje się środek pędzla przypisujemy wartość będącą '''minimum''' z tej list. Implementacja drugiej z tych definicji znajduje się poniżej. | ||
Aktualna wersja na dzień 13:25, 9 cze 2015
Spis treści
Morfologia matematyczna
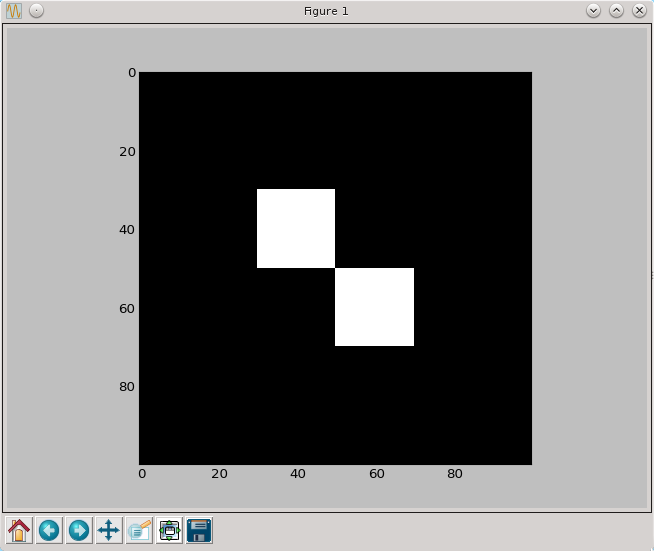
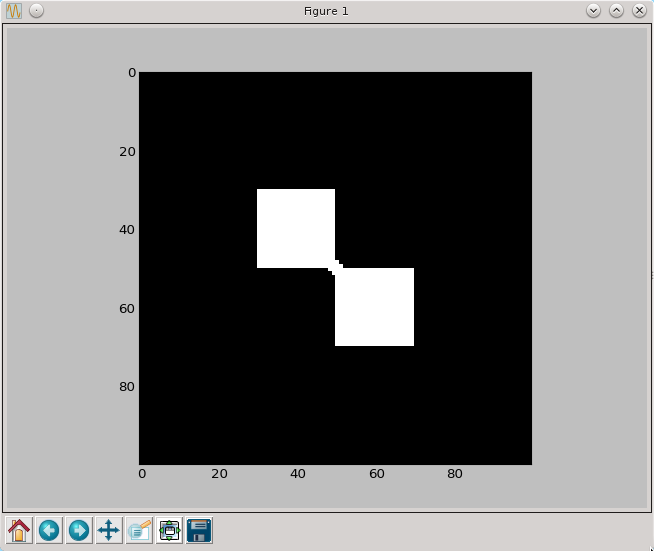
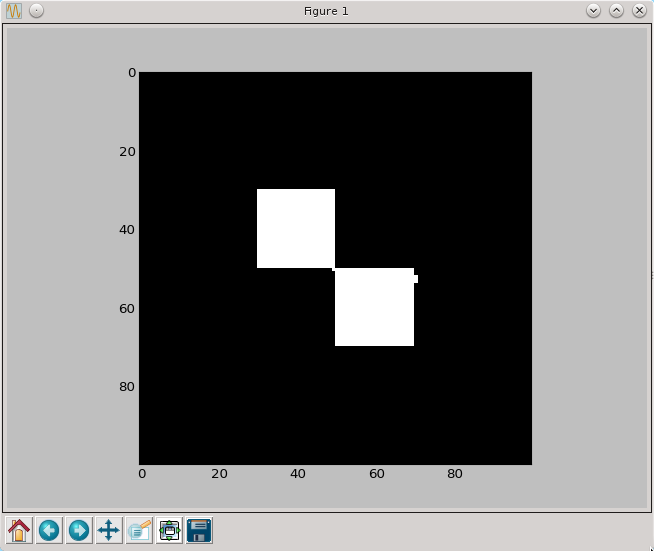
Morfologia matematyczna to bardzo przydatna metoda przetwarzania obrazów binarnych (czarno-białych), pozwalająca na analizę i "upraszczanie" obserwowanych kształtów. W szczególności można ją zastosować do obrazów medycznych przetworzonych przez progowanie. Metody morfologii matematycznej pozwalają także na uspójnienie otrzymanego obrazu nie zmieniając jego rozmiarów zewnętrznych co może być bardzo przydatne przy dokonywaniu pomiarów w oparciu o cyfrowy obraz medyczny. Dla osób zainteresowanych bardziej formalną definicją poszczególnych operacji polecam bardzo szeroką literaturę dostępną w internecie. Tutaj przedstawimy definicję pozwalającą na łatwiejsze zrozumienie istoty działania poszczególnych operacji. Operacje morfologii matematycznej opierają się na tak zwanym elemencie strukturalnym, który my w uproszczeniu nazywać będziemy pędzlem (brush). Zacznijmy od zdefiniowania naszego obrazu roboczego i przykładowego pędzla.
import numpy as np
import pylab as py
a=np.zeros((100,100),dtype=np.bool)
a[30:50,30:50]=True
a[50:70,50:70]=True
brush7=np.array([[0,0,1,1,1,0,0],[0,1,1,1,1,1,0],[1,1,1,1,1,1,1],[1,1,1,1,1,1,1],[1,1,1,1,1,1,1],[0,1,1,1,1,1,0],[0,0,1,1,1,0,0]],dtype=np.bool)
py.imshow(a, cmap=py.cm.gray, interpolation='nearest')
py.show()
W definiowaniu funkcji morfologii matematycznej przydatna będzie procedura zmieniająca pędzel, będący kwadratową tablicą zer i jedynek na listę wektorów mających początek w środku pędzla i końce we wszystkich komórkach posiadających wartość 1. Kod takiej procedury przedstawia się następująco.
def brush2list(brush):
result=[]
N=brush.shape[0]
middle=N/2
for x in range(N):
for y in range(N):
if brush[x,y]: result.append((x-middle,y-middle))
return result
Dylacja
Pierwszą operacją którą omówimy jest dylacja. Nasz obraz w chwili obecnej składa się z tła zer (w kolorze czarnym) i dwóch kwadratów z jedynek (w kolorze białym). Wyobraźmy sobie, że nasz pędzel służy do malowania po obrazku. Jeżeli w jakimś miejscu przyłożymy środek pędzla, to wszystkie pixele, na których znajdą się jedynki w pędzlu zmienią swoją wartość na jeden. Operacja dylacji to przyłożenie środka pędzla do wszystkich komórek, których początkowa wartość to jeden. Równoważna jest także inna definicja. Przykładamy środek pędzla po kolei do wszystkich pixeli. Tworzymy listę wartości pixeli obrazu, które w danym ułożeniu pędzla odpowiadając wartościom 1 na pędzlu. Do pixela w którym znajduje się środek pędzla przypisujemy wartość będącą maksimum z tej list. Implementacja drugiej z tych definicji znajduje się poniżej.
def dylacja(fig,brush=np.array([[0,1,0],[1,1,1],[0,1,0]],dtype=np.bool)):
result=np.zeros(fig.shape)
brush_list=brush2list(brush)
for x in range(3,fig.shape[0]-3):
for y in range (3,fig.shape[1]-3):
result[x,y]=max([fig[x+x_shift,y+y_shift] for (x_shift,y_shift) in brush_list])
return result
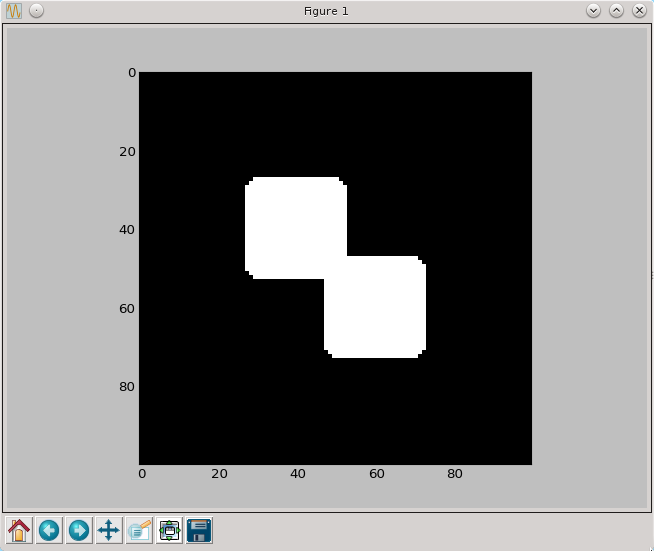
py.imshow(dylacja(a,brush7), cmap=py.cm.gray, interpolation='nearest')
py.show()
W efekcie dwa kwadraty powiększyły się i zaokrągliły im się rogi.
Erozja
Drugą operacją morfologii matematycznej jest erozja. Operacja jest analogiczna, z tą zmianą, że teraz nasz pędzel maluje na czarno i przesuwamy go po czarnych pixelach. Przy alternatywnej definicji przykładamy środek pędzla po kolei do wszystkich pixeli. Tworzymy listę wartości pixeli obrazu które w danym ułożeniu pędzla odpowiadając wartościom 1 na pędzlu. Do pixela w którym znajduje się środek pędzla przypisujemy wartość będącą minimum z tej list. Implementacja drugiej z tych definicji znajduje się poniżej.
def erozja(fig,brush=np.array([[0,1,0],[1,1,1],[0,1,0]],dtype=np.bool)):
result=np.zeros(fig.shape)
brush_list=brush2list(brush)
for x in range(3,fig.shape[0]-3):
for y in range (3,fig.shape[1]-3):
result[x,y]=min([fig[x+x_shift,y+y_shift] for (x_shift,y_shift) in brush_list])
return result
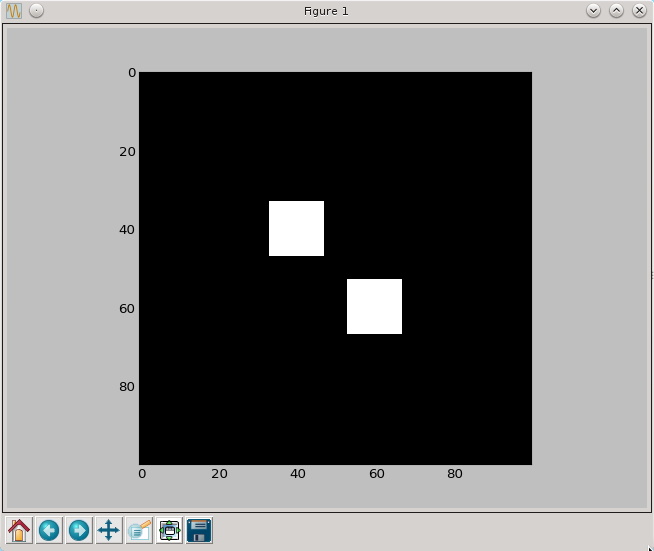
py.imshow(erozja(a,brush7), cmap=py.cm.gray, interpolation='nearest')
py.show()
W wyniku tej operacji kwadraty nie zmieniły swojego kształtu, za to zmniejszyły się i powstała między nimi przerwa.
Otwarcie i zamknięcie
Skoro dylacja powiększa rozmiar naszego obrazu a erozja zmniejsza, naturalnym jest postawienie sobie pytania, co się stanie gdy obraz najpierw potraktujemy erozją a potem dylacją lub też odwrotnie. Operacje powstałe właśnie w ten sposób nazywamy otwarciem i zamknięciem. Ich definicja nie jest już problematyczna posiadając implementacje wcześniejszych metod.
def otwarcie(fig,brush=np.array([[0,1,0],[1,1,1],[0,1,0]],dtype=np.bool)):
return dylacja(erozja(fig,brush),brush)
def zamkniecie(fig,brush=np.array([[0,1,0],[1,1,1],[0,1,0]],dtype=np.bool)):
return erozja(dylacja(fig,brush),brush)
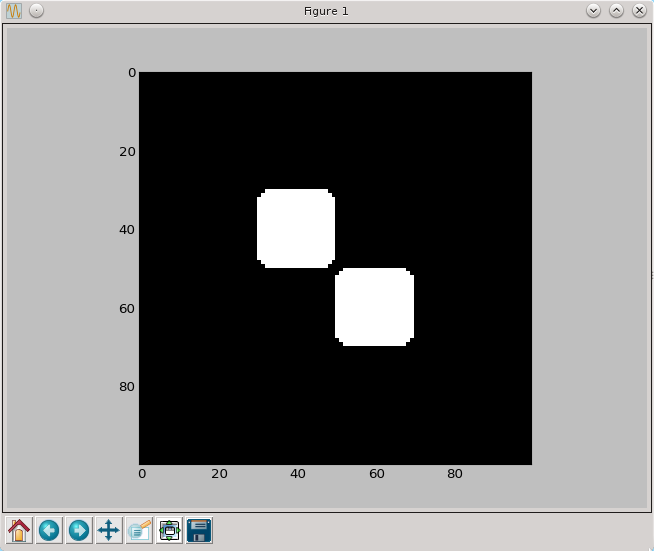
py.imshow(otwarcie(a,brush7), cmap=py.cm.gray, interpolation='nearest')
py.show()
py.imshow(zamkniecie(a,brush7), cmap=py.cm.gray, interpolation='nearest')
py.show()
Wyniki powyższych dwóch operacji są najbardziej przydatne w zastosowaniach medycznych. W obu przypadkach rozmiary obrazu nie zmieniły się. W przypadku otwarcia rogi kwadratów zaokrągliły się i stykające się kwadraty stały się wyraźniej rozłączne. W przypadku zamknięcia obszar tworzony przez dwa kwadraty został uspójniony tworząc coś w rodzaju "mostu" między nimi. Przy zastosowaniu zamknięcia wszystkie obiekty odległe od siebie o mniej niż średnica pędzla zostaną połączone.
Filtr medianowy
W poprzednich metodach przykładaliśmy środek pędzla po kolei do wszystkich pixeli, tworzyliśmy listę wartości pixeli obrazu, które w danym ułożeniu pędzla odpowiadają wartościom 1 na pędzlu. Do pixela, w którym znajduje się środek pędzla przypisujemy wartość będącą minimum lub maksimum z tej list. Co się stanie gdy na wartościach z tej listy wykonamy jakieś inne operacje? Wzięcie średniej, jak wspominałem w poprzednim rozdziale, doprowadzi do rozmycia obrazka (średnia nie musi być zerem lub jedynką). Bardzo przydatną operację uzyskamy, gdy weźmiemy medianę z wartości w tej liście. Powstanie w ten sposób tak zwany filtr medianowy, który jest doskonałym narzędziem do usuwania szumu z obrazka. Jego implementacja wygląda na przykład tak.
def medianowy(fig,brush=np.array([[0,1,0],[1,1,1],[0,1,0]],dtype=np.bool)):
result=np.zeros(fig.shape)
brush_list=brush2list(brush)
for x in range(3,fig.shape[0]-3):
for y in range (3,fig.shape[1]-3):
result[x,y]=np.median([fig[x+x_shift,y+y_shift] for (x_shift,y_shift) in brush_list])
return result
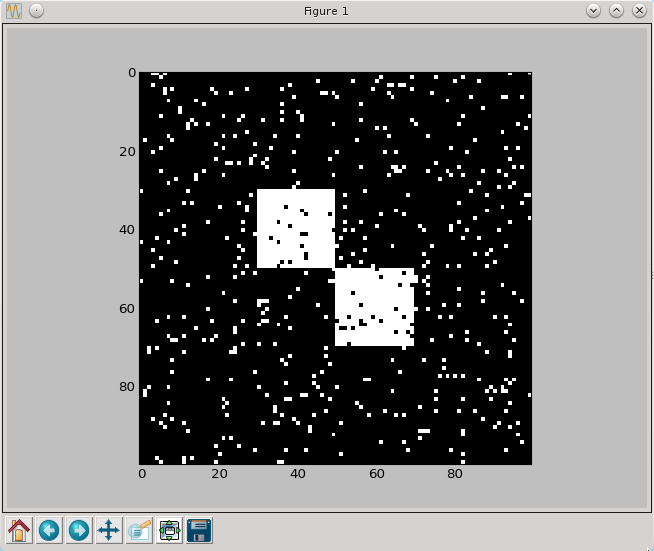
Aby przetestować działanie filtra medianowego musimy "zaszumić" nasz oryginalny obrazek
for x,y in np.ndindex(a.shape):
if (np.random.random()<0.05): a[x,y]=False
if (np.random.random()>0.95): a[x,y]=True
Zobaczmy teraz jakie wyniki da wielokrotne zastosowanie filtra medianowego.
py.imshow(a, cmap=py.cm.gray, interpolation='nearest')
py.show()
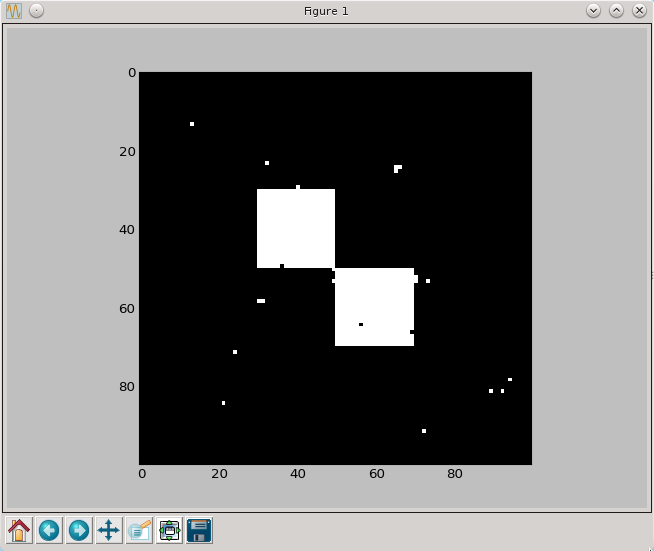
a=medianowy(a)
py.imshow(a, cmap=py.cm.gray, interpolation='nearest')
py.show()
a=medianowy(a)
py.imshow(a, cmap=py.cm.gray, interpolation='nearest')
py.show()
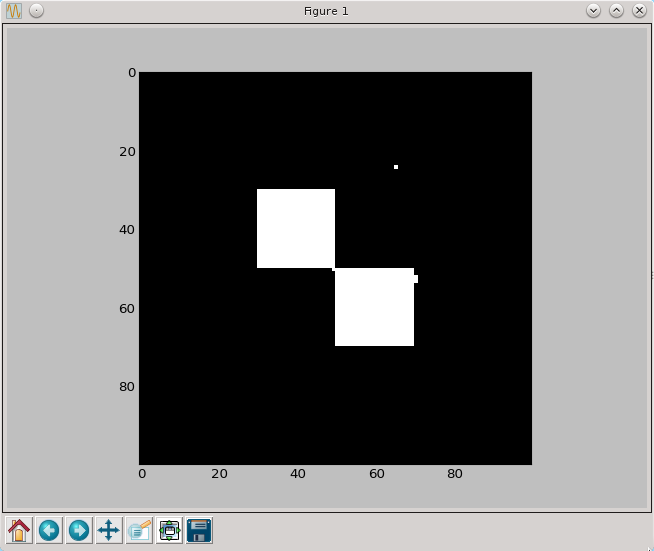
a=medianowy(a)
py.imshow(a, cmap=py.cm.gray, interpolation='nearest')
py.show()
Jak widać udało się odtworzyć kształty widoczne nawet na obrazku bardzo słabej jakości. Operacje takie pozwalają znacznie poprawić jakość wyników uzyskiwanych poprzez progowanie obrazów medycznych.