USG/Klasyczna rekonstrukcja: Różnice pomiędzy wersjami
| (Nie pokazano 13 wersji utworzonych przez 3 użytkowników) | |||
| Linia 1: | Linia 1: | ||
=Klasyczna rekonstrukcja obrazu (Beamforming)= | =Klasyczna rekonstrukcja obrazu (Beamforming)= | ||
Schemat nadawczy jest następujący. | Schemat nadawczy jest następujący. | ||
| − | [[Plik:Rys_przetworniki_nadawanie.png| | + | |
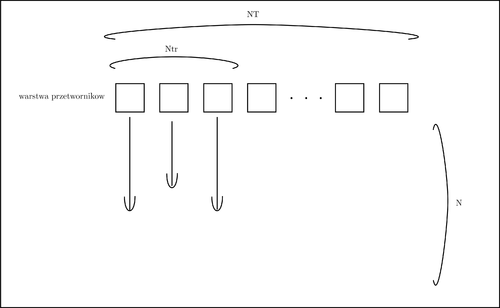
| + | [[Plik:Rys_przetworniki_nadawanie.png|500px|thumb|center|Wielkości odpowiadające wymiarom tablicy z danymi]] | ||
| + | |||
| + | W każdym nadaniu przetworniki subapertury nadawczej generują wiązkę o stałym ognisku. Subaperturę nadawczą w <math>n</math>-tym nadaniu tworzą przetworniki od <math>n</math>-tego do <math>(n+N_{tr})</math>-tego (gdzie <math>N_{tr}</math> - to liczba przetworników subapertury nadawczej). Zakładamy, że ognisko położone jest na osi centralnej subapertury nadawczej. Kształt wiązki otrzymujemy przez zastosowanie odpowiednich opóźnień nadawczych pomiędzy przetwornikami. Od momentu nadania wszystkie przetworniki (pełna apertura odbiorcza) rejestrują sygnał. Rejestracja sygnału trwa do <math>N</math>-tego okresu częstotliwości próbkowania - wielkość ta odpowiada maksymalnej głębokości obrazowania <math>D</math> w przybliżeniu zgodnie ze wzorem: | ||
| + | |||
| + | <math>D=\frac{N\cdot c}{2f_{s}} </math> | ||
| + | |||
| + | gdzie <math>f_{s}</math> - częstotliwość próbkowania; <math>c</math> - średnia prędkość dźwięku w ośrodku. <br> | ||
| + | Subapertura nadawcza przesuwana jest w kolejnych emisjach o 1 przetwornik. | ||
Parametry potrzebne do dalszej pracy: | Parametry potrzebne do dalszej pracy: | ||
| + | |||
<source lang = python> | <source lang = python> | ||
f0 = 5.5e6 # Częstotliwość nadawcza przetworników [Hz] | f0 = 5.5e6 # Częstotliwość nadawcza przetworników [Hz] | ||
| Linia 15: | Linia 24: | ||
</source> | </source> | ||
| − | Ponadto, do rekonstrukcji wykorzystywać będziemy prędkość dźwięku w ośrodku. Zakładamy, że jest ona stała. Dla pomiarów w fantomie cystowym proszę założyć: | + | [[Plik:Rys_fantom_cystowy.png|500px|thumb|center|Zdjęcie fantomu cystowego wraz ze schematem obrazującym przekrój fantomu w przybliżeniu odpowiadający płaszczyźnie obrazowania]] |
| + | |||
| + | [[Plik:Rys_fantom_nitkowy.png|500px|thumb|center|Zdjęcie fantomu nitkowego z góry. Płaszczyzna obrazowania jest umiejscowiona w przybliżeniu prostopadle do kierunku nitek. Dane zebrane były dla fantomu położonego w zbiorniku wody.]] | ||
| + | |||
| + | Ponadto, do rekonstrukcji wykorzystywać będziemy prędkość dźwięku w ośrodku. Zakładamy, że jest ona stała. Rekonstrukcję przeprowadzać będziemy dla danych z eksperymentów in vitro na dwóch fantomach - nitkowym oraz cystowym. Fantom nitkowy składa się z matrycy żyłek położonych w równych od odstępach, które umieszczone są następnie w zbiorniku wodnym. Płaszczyzna obrazowania przecina żyłki prostopadle, w efekcie czego na obrazie ultradźwiękowym każdej nitce odpowiadać powinien obiekt punktowy o jasności większej od jasności tła. <br> | ||
| + | Fantom cystowy składa się z materiału o właściwościach akustycznych (prędkość dźwięku w ośrodku, tłumienie itp.) zbliżonych do tkanki ludzkiej; w materiale tym umieszczone są cysty. Cysty te widoczne będą na obrazie ultradźwiękowym jako owalne obiekty o jasności mniejszej od jasności tła (cysta rozprasza mniej niż tło). | ||
| + | Dla pomiarów w fantomie cystowym proszę założyć: | ||
| + | |||
<source lang = python> | <source lang = python> | ||
c = 1540 # [m/s] | c = 1540 # [m/s] | ||
| Linia 33: | Linia 49: | ||
==Dane RF== | ==Dane RF== | ||
| − | Do dyspozycji mamy dwa zestawy danych RF z pomiarów na fantomie nitkowym (plik usg1_nitki.npy) i na fantomie cystowym ( | + | Do dyspozycji mamy dwa zestawy danych RF z pomiarów na fantomie nitkowym ([http://www.fuw.edu.pl/~jarekz/FUW-FID-2016/raw-data/usg1_sta_nitki.npy plik usg1_nitki.npy]) i na fantomie cystowym ([http://www.fuw.edu.pl/~jarekz/FUW-FID-2016/raw-data/usg1_sta_cysty.npy plik usg1_cysty.npy]). |
| − | + | Zaczniemy od wczytania oraz wyświetlenia (funkcja plot) surowych danych RF (przed rekonstrukcją obrazu). Dane możemy wczytać za pomocą poleceń | |
| − | + | ||
| − | Zaczniemy od wczytania oraz | ||
<source lang = python> | <source lang = python> | ||
RF=np.load('usg1_nitki.npy') | RF=np.load('usg1_nitki.npy') | ||
</source> | </source> | ||
| − | Dostaliśmy tablicę o wymiarach <math>NT\times N \times NT-N_{tr} </math> gdzie <math>N</math> odpowiada czasowi rejestracji danych z pojedynczego nadania. | + | |
| + | Dostaliśmy tablicę o wymiarach <math>NT\times N \times (NT-N_{tr}) </math> gdzie <math>N</math> odpowiada czasowi rejestracji danych z pojedynczego nadania. | ||
Proszę podejrzeć dane zebrane dla kilku strzałów (np. pierwszego i ostatniego). Dla przejrzystości proszę podejrzeć jedynie pierwsze 300 próbek: | Proszę podejrzeć dane zebrane dla kilku strzałów (np. pierwszego i ostatniego). Dla przejrzystości proszę podejrzeć jedynie pierwsze 300 próbek: | ||
| + | |||
<source lang = python> | <source lang = python> | ||
py.subplot(2, 1, 1) | py.subplot(2, 1, 1) | ||
| − | py.imshow(RF[:, :300, 0] | + | py.imshow(RF[:, :300, 0]) |
py.subplot(2, 1, 2) | py.subplot(2, 1, 2) | ||
| − | py.imshow(RF[:, :300, -1] | + | py.imshow(RF[:, :300, -1]) |
py.show() | py.show() | ||
</source> | </source> | ||
| + | |||
Jak zmieniają się sygnały między kolejnymi strzałami? | Jak zmieniają się sygnały między kolejnymi strzałami? | ||
Czy na podstawie samych surowych danych widoczna jest oczekiwana struktura (obrazowane obiekty)? | Czy na podstawie samych surowych danych widoczna jest oczekiwana struktura (obrazowane obiekty)? | ||
| Linia 54: | Linia 72: | ||
==Opóźnienia nadawczo-odbiorcze== | ==Opóźnienia nadawczo-odbiorcze== | ||
| − | Z danych zebranych dla pojedynczego nadania rekonstruować będziemy pojedynczą linię obrazu. Wykorzystamy do tego sygnału z tych samych przetworników, które nadawały (subapertura odbiorcza). Wartość sygnału pojedynczego piksela otrzymamy sumując sygnały z tych przetworników przesunięte zgodnie z określonymi opóźnieniami odbiorczymi. Sygnał <math>S_{(i,j)}</math> dla piksela w <math>i</math>-tej linii i głębokości <math>j</math> otrzymujemy jako | + | Z danych zebranych dla pojedynczego nadania rekonstruować będziemy pojedynczą linię obrazu. Wykorzystamy do tego sygnału z tych samych przetworników, które nadawały (subapertura odbiorcza). Wartość sygnału pojedynczego piksela otrzymamy sumując sygnały z tych przetworników przesunięte zgodnie z określonymi opóźnieniami odbiorczymi. Sygnał <math>S_{(i,j)}</math> dla piksela w <math>i</math>-tej linii i głębokości <math>j</math> otrzymujemy jako |
| − | <math>S_{(i,j)}=\sum^{N_{tr}-1}_{k=0} s_{i,k}(j+t_{i}(k)))</math> | + | |
| + | <math>S_{(i,j)}=\sum^{N_{tr}-1}_{k=0} s_{i,k}(j+t_{i}(k)))</math>, | ||
| + | |||
gdzie <math>s_{i,k}(t)</math> - sygnał z <math>i</math>-tego nadania i <math>k</math>-tego przetwornika w chwili <math>t</math>;<br> | gdzie <math>s_{i,k}(t)</math> - sygnał z <math>i</math>-tego nadania i <math>k</math>-tego przetwornika w chwili <math>t</math>;<br> | ||
<math>t_{i}(k)</math> - opóźnienie nadawczo-odbiorcze <math>k</math>-tego przetwornika w <math>i</math>-tym nadaniu.<br> | <math>t_{i}(k)</math> - opóźnienie nadawczo-odbiorcze <math>k</math>-tego przetwornika w <math>i</math>-tym nadaniu.<br> | ||
| Linia 64: | Linia 84: | ||
==Rekonstrukcja obrazu== | ==Rekonstrukcja obrazu== | ||
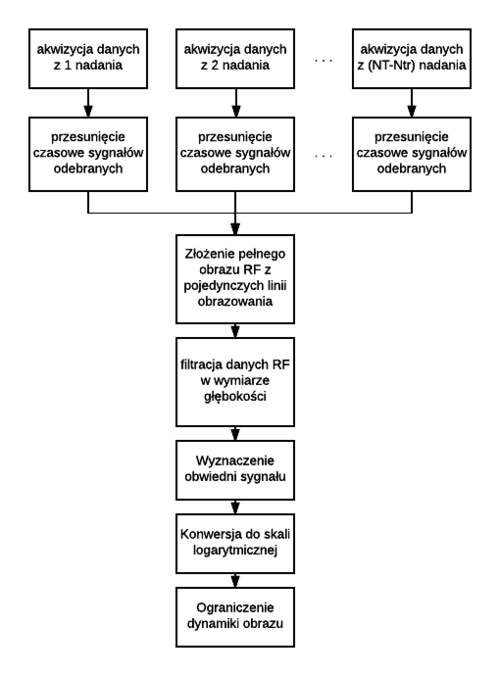
| + | [[Plik:schemat_rekonstrukcji.png|500px|thumb|center|Schemat blokowy tworzenia obrazu]] | ||
Mając już do dyspozycji opóźnienia nadawcze dla interesującego nas punktu ogniskowania możemy przystąpić do rekonstrukcji obrazu. Proszę napisać skrypt dokonujący w pętli rekonstrukcji kolejnych linii obrazu. | Mając już do dyspozycji opóźnienia nadawcze dla interesującego nas punktu ogniskowania możemy przystąpić do rekonstrukcji obrazu. Proszę napisać skrypt dokonujący w pętli rekonstrukcji kolejnych linii obrazu. | ||
| − | + | ||
Zrekonstruowany obraz przedstawiamy w skali decybelowej. Można wykonać to np. przy użyciu przykładowego kodu: | Zrekonstruowany obraz przedstawiamy w skali decybelowej. Można wykonać to np. przy użyciu przykładowego kodu: | ||
| + | |||
<source lang=python> | <source lang=python> | ||
| − | #tablica img przechowuje zrekonstruowany obraz | + | # tablica img przechowuje zrekonstruowany obraz |
indices = img>0 | indices = img>0 | ||
indices2 = img<0 | indices2 = img<0 | ||
| − | + | # wybieramy indeksy którym odpowiadają niezerowe wartości | |
| + | # - w przeciwnym wypadku operacja logarytmowania byłaby niejednoznaczna | ||
| + | indices = indices + indices2 | ||
img = np.abs(img)/np.max(np.abs(img[indices])) | img = np.abs(img)/np.max(np.abs(img[indices])) | ||
img[indices] = 10*np.log(img[indices]) | img[indices] = 10*np.log(img[indices]) | ||
| Linia 78: | Linia 102: | ||
===Zakres dynamiki=== | ===Zakres dynamiki=== | ||
Istotny wpływ na wygląd ostatecznego obrazu ma dobór zakresu dynamiki wyświetlanych wartości. Na początek proszę wyświetlić obraz w pełnej dynamice. <br> | Istotny wpływ na wygląd ostatecznego obrazu ma dobór zakresu dynamiki wyświetlanych wartości. Na początek proszę wyświetlić obraz w pełnej dynamice. <br> | ||
| − | Do wyświetlenia obrazu wykorzystamy bibliotekę PIL, która pozwala nam na łatwe interpolowanie obrazu (przeskalowanie osi) | + | Do wyświetlenia obrazu wykorzystamy bibliotekę PIL, która pozwala nam na łatwe interpolowanie obrazu (przeskalowanie osi). Zwróćmy uwagę, że w naszym schemacie bezpośrednio po rekonstrukcji mamy obraz z zaburzonymi proporcjami - częstotliwość w głębokości związana jest z częstotliwością próbkowania, zaś częstotliwość w szerokości związana jest z odległością między przetwornikami (pitch). |
<source lang=python> | <source lang=python> | ||
| Linia 89: | Linia 113: | ||
Następnie proszę rozważyć ograniczenie dynamiki obrazu np. 60dB (zakres od -60dB do 0). Ograniczenie dynamiki jest równoważne z zastosowaniem funkcji progowej | Następnie proszę rozważyć ograniczenie dynamiki obrazu np. 60dB (zakres od -60dB do 0). Ograniczenie dynamiki jest równoważne z zastosowaniem funkcji progowej | ||
| + | |||
<source lang=python> | <source lang=python> | ||
indices = img <-low | indices = img <-low | ||
| Linia 95: | Linia 120: | ||
img[indices] = 0 | img[indices] = 0 | ||
</source> | </source> | ||
| − | |||
| − | Czy na obrazach widoczna jest oczekiwana struktura? Jak zakres dynamiki wpływa na obraz? | + | Czy na obrazach widoczna jest oczekiwana struktura? Jak zakres dynamiki wpływa na obraz? |
===Filtrowanie obrazu=== | ===Filtrowanie obrazu=== | ||
Aby otrzymać czytelny obraz często niezbędne jest przefiltrowanie obrazu. Proszę wykonać filtrowanie dolno- i górnoprzepustowe obrazu wzdłuż głębokości, np. według poleceń: | Aby otrzymać czytelny obraz często niezbędne jest przefiltrowanie obrazu. Proszę wykonać filtrowanie dolno- i górnoprzepustowe obrazu wzdłuż głębokości, np. według poleceń: | ||
| + | |||
<source lang=python> | <source lang=python> | ||
b, a = sig.butter(10, 0.2, 'highpass') | b, a = sig.butter(10, 0.2, 'highpass') | ||
| Linia 107: | Linia 132: | ||
img = sig.filtfilt(b, a, img,axis=1) | img = sig.filtfilt(b, a, img,axis=1) | ||
</source> | </source> | ||
| + | |||
Jak zmienił się obraz po zastosowaniu filtrów? Proszę zbadać jak parametry filtra wpływają na końcowy obraz. | Jak zmienił się obraz po zastosowaniu filtrów? Proszę zbadać jak parametry filtra wpływają na końcowy obraz. | ||
| Linia 112: | Linia 138: | ||
Uzyskanie wynikowego obrazu B-mode (ang. Brightness) ze zrekonstruowanego obrazu RF polega na wyznaczeniu obwiedni sygnałów RF. | Uzyskanie wynikowego obrazu B-mode (ang. Brightness) ze zrekonstruowanego obrazu RF polega na wyznaczeniu obwiedni sygnałów RF. | ||
Typowo do jej wyznaczenia stosuje się transformację Hilberta. Przykładowy skrypt zamieniający każdą linię obrazu na jej obwiednię | Typowo do jej wyznaczenia stosuje się transformację Hilberta. Przykładowy skrypt zamieniający każdą linię obrazu na jej obwiednię | ||
| + | |||
<source lang=python> | <source lang=python> | ||
for p in range(np.shape(RF)[2]): | for p in range(np.shape(RF)[2]): | ||
img[p, :] = np.abs(sig.hilbert(img[p, :])) | img[p, :] = np.abs(sig.hilbert(img[p, :])) | ||
</source> | </source> | ||
| + | |||
Proszę porównać obraz RF po rekonstrukcji oraz obraz B-mode. Czym się one różnią? Czy informacja utracona w czasie przejścia do obwiedni mogła być istotna z punktu widzenia obrazowania medycznego? | Proszę porównać obraz RF po rekonstrukcji oraz obraz B-mode. Czym się one różnią? Czy informacja utracona w czasie przejścia do obwiedni mogła być istotna z punktu widzenia obrazowania medycznego? | ||
Aktualna wersja na dzień 10:06, 6 paź 2016
Spis treści
Klasyczna rekonstrukcja obrazu (Beamforming)
Schemat nadawczy jest następujący.
W każdym nadaniu przetworniki subapertury nadawczej generują wiązkę o stałym ognisku. Subaperturę nadawczą w [math]n[/math]-tym nadaniu tworzą przetworniki od [math]n[/math]-tego do [math](n+N_{tr})[/math]-tego (gdzie [math]N_{tr}[/math] - to liczba przetworników subapertury nadawczej). Zakładamy, że ognisko położone jest na osi centralnej subapertury nadawczej. Kształt wiązki otrzymujemy przez zastosowanie odpowiednich opóźnień nadawczych pomiędzy przetwornikami. Od momentu nadania wszystkie przetworniki (pełna apertura odbiorcza) rejestrują sygnał. Rejestracja sygnału trwa do [math]N[/math]-tego okresu częstotliwości próbkowania - wielkość ta odpowiada maksymalnej głębokości obrazowania [math]D[/math] w przybliżeniu zgodnie ze wzorem:
[math]D=\frac{N\cdot c}{2f_{s}} [/math]
gdzie [math]f_{s}[/math] - częstotliwość próbkowania; [math]c[/math] - średnia prędkość dźwięku w ośrodku.
Subapertura nadawcza przesuwana jest w kolejnych emisjach o 1 przetwornik.
Parametry potrzebne do dalszej pracy:
f0 = 5.5e6 # Częstotliwość nadawcza przetworników [Hz]
fs = 50e6 # Częstotliwość próbkowania [Hz]
pitch = 0.21e-3 # Deklarowana odległość między środkami przetworników nadawczo-odbiorczych (tzw. pitch) [m]
NT = 192 # Liczba przetworników głowicy (pełna apertura)
Ntr = 64 # Liczba przetworników aktywnej subapertury
Rf1 = 40e-3 # Położenie ogniska wiązki nadawczej od środka subapertury nadawczej [m]
Ponadto, do rekonstrukcji wykorzystywać będziemy prędkość dźwięku w ośrodku. Zakładamy, że jest ona stała. Rekonstrukcję przeprowadzać będziemy dla danych z eksperymentów in vitro na dwóch fantomach - nitkowym oraz cystowym. Fantom nitkowy składa się z matrycy żyłek położonych w równych od odstępach, które umieszczone są następnie w zbiorniku wodnym. Płaszczyzna obrazowania przecina żyłki prostopadle, w efekcie czego na obrazie ultradźwiękowym każdej nitce odpowiadać powinien obiekt punktowy o jasności większej od jasności tła.
Fantom cystowy składa się z materiału o właściwościach akustycznych (prędkość dźwięku w ośrodku, tłumienie itp.) zbliżonych do tkanki ludzkiej; w materiale tym umieszczone są cysty. Cysty te widoczne będą na obrazie ultradźwiękowym jako owalne obiekty o jasności mniejszej od jasności tła (cysta rozprasza mniej niż tło).
Dla pomiarów w fantomie cystowym proszę założyć:
c = 1540 # [m/s]
zaś dla pomiarów w fantomie nitkowym
c = 1490 # prędkość dźwięku w wodzie destylowanej [m/s]
Będziemy korzystać z bibliotek:
import numpy as np
import pylab as py
import scipy.signal as sig
from PIL import ImageTk, Image
Dane RF
Do dyspozycji mamy dwa zestawy danych RF z pomiarów na fantomie nitkowym (plik usg1_nitki.npy) i na fantomie cystowym (plik usg1_cysty.npy). Zaczniemy od wczytania oraz wyświetlenia (funkcja plot) surowych danych RF (przed rekonstrukcją obrazu). Dane możemy wczytać za pomocą poleceń
RF=np.load('usg1_nitki.npy')
Dostaliśmy tablicę o wymiarach [math]NT\times N \times (NT-N_{tr}) [/math] gdzie [math]N[/math] odpowiada czasowi rejestracji danych z pojedynczego nadania. Proszę podejrzeć dane zebrane dla kilku strzałów (np. pierwszego i ostatniego). Dla przejrzystości proszę podejrzeć jedynie pierwsze 300 próbek:
py.subplot(2, 1, 1)
py.imshow(RF[:, :300, 0])
py.subplot(2, 1, 2)
py.imshow(RF[:, :300, -1])
py.show()
Jak zmieniają się sygnały między kolejnymi strzałami? Czy na podstawie samych surowych danych widoczna jest oczekiwana struktura (obrazowane obiekty)? Jak zmienia się energia sygnałów dla różnych przetworników odbiorczych zależnie od odległości od środka subapertury?
Opóźnienia nadawczo-odbiorcze
Z danych zebranych dla pojedynczego nadania rekonstruować będziemy pojedynczą linię obrazu. Wykorzystamy do tego sygnału z tych samych przetworników, które nadawały (subapertura odbiorcza). Wartość sygnału pojedynczego piksela otrzymamy sumując sygnały z tych przetworników przesunięte zgodnie z określonymi opóźnieniami odbiorczymi. Sygnał [math]S_{(i,j)}[/math] dla piksela w [math]i[/math]-tej linii i głębokości [math]j[/math] otrzymujemy jako
[math]S_{(i,j)}=\sum^{N_{tr}-1}_{k=0} s_{i,k}(j+t_{i}(k)))[/math],
gdzie [math]s_{i,k}(t)[/math] - sygnał z [math]i[/math]-tego nadania i [math]k[/math]-tego przetwornika w chwili [math]t[/math];
[math]t_{i}(k)[/math] - opóźnienie nadawczo-odbiorcze [math]k[/math]-tego przetwornika w [math]i[/math]-tym nadaniu.
W klasycznej metodzie beamformingu do rekonstrukcji wykorzystujemy takie same opóźnienia jak te użyte przy nadawaniu. Funkcja powinna dla zadanej liczby przetworników i odległości ogniska położonego w punkcie [math](x,y)[/math] generować tablicę opóźnień, gdzie opóźnienie dla przetwornika położonego w punkcie [math](a,b)[/math] określone jest jako [math]\sqrt{(x-a)^2+(y-b)^2}/c [/math] Proszę pamiętać, że opóźnienia w powyższym wzorze są podane w sekundach - podczas gdy do dalszych obliczeń wygodniejsze może okazać się wykorzystanie wartości liczonych w okresach próbkowania.
Rekonstrukcja obrazu
Mając już do dyspozycji opóźnienia nadawcze dla interesującego nas punktu ogniskowania możemy przystąpić do rekonstrukcji obrazu. Proszę napisać skrypt dokonujący w pętli rekonstrukcji kolejnych linii obrazu.
Zrekonstruowany obraz przedstawiamy w skali decybelowej. Można wykonać to np. przy użyciu przykładowego kodu:
# tablica img przechowuje zrekonstruowany obraz
indices = img>0
indices2 = img<0
# wybieramy indeksy którym odpowiadają niezerowe wartości
# - w przeciwnym wypadku operacja logarytmowania byłaby niejednoznaczna
indices = indices + indices2
img = np.abs(img)/np.max(np.abs(img[indices]))
img[indices] = 10*np.log(img[indices])
Zakres dynamiki
Istotny wpływ na wygląd ostatecznego obrazu ma dobór zakresu dynamiki wyświetlanych wartości. Na początek proszę wyświetlić obraz w pełnej dynamice.
Do wyświetlenia obrazu wykorzystamy bibliotekę PIL, która pozwala nam na łatwe interpolowanie obrazu (przeskalowanie osi). Zwróćmy uwagę, że w naszym schemacie bezpośrednio po rekonstrukcji mamy obraz z zaburzonymi proporcjami - częstotliwość w głębokości związana jest z częstotliwością próbkowania, zaś częstotliwość w szerokości związana jest z odległością między przetwornikami (pitch).
Frame = Image.fromarray(np.uint8(cm.Greys(img.transpose())*255))
width = NT*pitch
depth = N*c/fs
Frame = Frame.resize((int(N*width/depth)*2, N), Image.BICUBIC)
Frame.show()
Następnie proszę rozważyć ograniczenie dynamiki obrazu np. 60dB (zakres od -60dB do 0). Ograniczenie dynamiki jest równoważne z zastosowaniem funkcji progowej
indices = img <-low
img[indices] = -low
indices = img >= 0
img[indices] = 0
Czy na obrazach widoczna jest oczekiwana struktura? Jak zakres dynamiki wpływa na obraz?
Filtrowanie obrazu
Aby otrzymać czytelny obraz często niezbędne jest przefiltrowanie obrazu. Proszę wykonać filtrowanie dolno- i górnoprzepustowe obrazu wzdłuż głębokości, np. według poleceń:
b, a = sig.butter(10, 0.2, 'highpass')
img = sig.filtfilt(b, a, img,axis=1)
b, a = sig.butter(10, 0.9, 'lowpass')
img = sig.filtfilt(b, a, img,axis=1)
Jak zmienił się obraz po zastosowaniu filtrów? Proszę zbadać jak parametry filtra wpływają na końcowy obraz.
Obraz B-mode
Uzyskanie wynikowego obrazu B-mode (ang. Brightness) ze zrekonstruowanego obrazu RF polega na wyznaczeniu obwiedni sygnałów RF. Typowo do jej wyznaczenia stosuje się transformację Hilberta. Przykładowy skrypt zamieniający każdą linię obrazu na jej obwiednię
for p in range(np.shape(RF)[2]):
img[p, :] = np.abs(sig.hilbert(img[p, :]))
Proszę porównać obraz RF po rekonstrukcji oraz obraz B-mode. Czym się one różnią? Czy informacja utracona w czasie przejścia do obwiedni mogła być istotna z punktu widzenia obrazowania medycznego?
Położenie ogniska
W czasie rekonstrukcji założyliśmy, że ognisko wiązki nadawczej położone było zawsze w określonej odległości od środka subapertury nadawczej. Proszę zbadać:
- Jak zmienia się ostrość obrazu w zależności od głębokości? Na jakiej głębokości rozdzielczość obrazu wydaje się być najlepsza?
- Proszę zrekonstruować obraz ponownie zakładając inną odległość ogniska nadawczego (np. dwa razy mniejszą). Jak zmienił się obraz?