Uczenie maszynowe i sztuczne sieci neuronowe/Wykład 3: Różnice pomiędzy wersjami
(Utworzono nową stronę "Kategoria: Uczenie maszynowe i sztuczne sieci neuronowe =Nieliniowość= Nowością wprowadzoną przez Perceptron(Rosenblatt 1958) w stosunku do sieci MADALINE, był...") |
m |
||
| (Nie pokazano 2 pośrednich wersji utworzonych przez tego samego użytkownika) | |||
| Linia 1: | Linia 1: | ||
| − | [[ | + | [[Uczenie_maszynowe_i_sztuczne_sieci_neuronowe|powrót]] |
=Nieliniowość= | =Nieliniowość= | ||
Nowością wprowadzoną przez Perceptron(Rosenblatt 1958) w stosunku do sieci MADALINE, było zastosowanie elementu nieliniowego. W perceptronie wyjście neuronu: | Nowością wprowadzoną przez Perceptron(Rosenblatt 1958) w stosunku do sieci MADALINE, było zastosowanie elementu nieliniowego. W perceptronie wyjście neuronu: | ||
| Linia 34: | Linia 34: | ||
\end{array} | \end{array} | ||
\right\} | \right\} | ||
| − | + | jesli | |
\left\{ | \left\{ | ||
\begin{array}{l} | \begin{array}{l} | ||
Aktualna wersja na dzień 16:32, 16 lut 2017
Spis treści
Nieliniowość
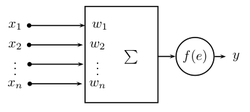
Nowością wprowadzoną przez Perceptron(Rosenblatt 1958) w stosunku do sieci MADALINE, było zastosowanie elementu nieliniowego. W perceptronie wyjście neuronu:
- [math] y = f(e)[/math]
gdzie pobudzenie
- [math] e = \sum_{i=1}^n w_ix_i + w_0 = \sum_{i=0}^n w_ix_i \quad \Leftarrow x_0 := 1 [/math]
Pobudzenie neuronu w postaci ważonej sumy wejść nie jest jedynym możliwym, mogą to być np.:
- [math]e^{(j+1)} = e^{(j)} + \sum_{i=0}^n w^{(j)}x^{(j)}[/math]
lub
- [math]e = \prod_{i=1}^n w_ix_i[/math]
Dla własności neuronu największe znaczenie ma jednak forma nieliniowości [math]f(.)[/math].
Perceptron Rosenblatta
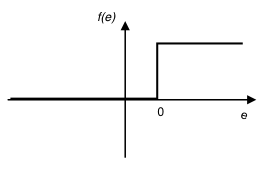
Najprostsza pojęciowo postać nieliniowości:
- [math]y = \left\{ \begin{array}{lcl} 1 \quad & \text{dla} & e \ge 0\\ 0 \quad & \text{dla} & e \lt 0 \end{array} \right. [/math]
Interpretacja geometryczna: perceptron prosty działa jak dyskryminator liniowy.
- [math] x \;jest\; klasy \left\{ \begin{array}{l} 1 \\ 0 \end{array} \right\} jesli \left\{ \begin{array}{l} y = 1, e \ge 0\\ y = 0, e \lt 0 \end{array} \right\} [/math]
Obszar, w którym perceptron zwraca 1 — podejmuje decyzję tak jest ograniczony tworem o równaniu:
- [math] \sum_{i=1}^n w_i x_i + w_0 = 0 [/math]
Dla n = 2 jest to prosta, dla n = 3 płaszczyzna, w ogólności rozmaitość liniowa stopnia n − 1 hiperpłaszczyzna.
Przykład
Rozważmy perceptron z trzema wagami [math]w = [-6, 2, 3][/math] pobudzenie neuronu:
- [math]e = W X = [-6,2,3] \left[ \begin{array}{l} 1\\ x_1 \\ x_2 \end{array} \right] = -6 + 2x_1 + 3x_2 [/math]
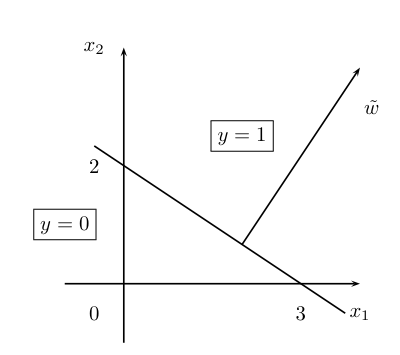
We właściwej przestrzeni wejść(tzn. [math][x_1,x_2][/math]) hiperpowierzchnia podejmowania decyzji jest prostą o równaniu:
- [math]2x_1 + 3x_2 - 6 = 0[/math]
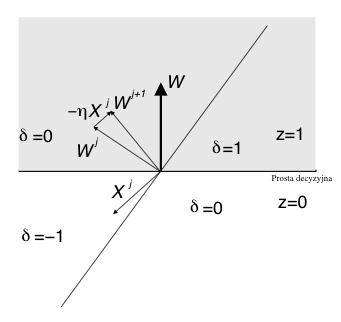
Obcięty wektor wag [math]\tilde w = [2, 3][/math] jest prostopadły do prostej podejmowania decyzji. Wektor wag jest skierowany w stronę, gdzie y = 1.
Dobieranie wag perceptronu prostego
Wagi perceptronu prostego można dobrać na dwa sposoby:
- możemy obliczyć wagi neuronów lub
- znaleźć je w procesie iteracyjnego uczenia.
- Obliczanie
Korzystamy z tego, że wektor w jest ortogonalny do hiperpłaszczyzny podejmowania decyzji, zatem musi spełniać równanie:
- [math]w x = 0 \rightarrow \sum_{i=1}^n w_i x_i + w_0 = 0 [/math]
także "obcięty" wektor wag [math]\tilde w = [w_1,\dots, w_n][/math] jest ortogonalny do "obciętych" wektorów wejściowych [math]\tilde x = [x_1,\dots,x_n]^T[/math] bo:
- [math]\forall_{ a,b}\quad w x^{(a)} - w x^{(b)} = 0[/math]
zatem
- [math]\forall_{ a,b}\quad (\tilde w \tilde x^{(a)} +w_0) - (\tilde w \tilde x^{(b)} +w_0) = \tilde w\tilde x^{(a)} - \tilde w \tilde x^{(b)} = 0[/math]
Aby powyższa równość zachodziła musi zachodzić:
- [math]\forall_{ a}\quad \tilde w \tilde x^{(a)} = 0[/math]
Przykład: Bramka NAND
Obliczmy wagi perceptronu realizującego funkcję logiczną NAND. Jej tabela wartości logicznych jest następująca:
| [math]x_1[/math] | 0 0 1 1 |
| [math]x_2[/math] | 0 1 0 1 |
| [math]y[/math] | 1 1 1 0 |
|---|
Spójrzmy na reprezentację graficzną:
Można zaproponować następującą prostą podejmowania decyzji:
- [math] x_1 + x_2 - 1.5 = 0 [/math]
wektor wag [math][w_1 , w_2 ][/math] jest prostopadły do tej prostej i skierowany w stronę gdzie [math]y = 1[/math], więc:
- [math] [w_1 , w_2 ] = [-1, -1][/math]
i wybieramy
- [math]w_0 = 1.5[/math].
Ostatecznie [math]w = [1.5, -1, -1][/math]
Uczenie perceptronu
Algorytm uczenia perceptronu jest formalnie bardzo podobny do algorytmu spadku gradientowego. Mamy ciąg uczący:
- [math] \left\{ X^{(j)}, z^{(j)} \right\}_{j=1,\dots,M}[/math]
i regułę zmiany wag po zaprezentowaniu j-tego przykładu (reguła ta nazywana jest "regułą delta"):
- [math]W^{(j+1)} = W^{(j)} + \eta\delta^{(j)}X^{(j)}[/math]
gdzie [math]\delta^{(j)}[/math] jest błędem perceptronu dla j-tego przykładu:
- [math]\delta^{(j)} = z^{(j)} - y^{(j)}[/math]
Istotną różnicę stanowi fakt, że:
- [math] y = \{0,1\}[/math],
a co za tym idzie błąd może przyjmować tylko wartości dyskretne:
- [math]\delta = \{-1,0,+1\}[/math]
Dlaczego ten algorytm działa?
Ponieważ wejścia i wyjścia mogą przyjmować tylko kilka wartości możemy prześledzić wszystkie przypadki. Są tylko 4 możliwości zmiany wag:
| [math]z^{(j)}[/math] | [math] y^{(j)}[/math] | [math]\delta^{(j)}[/math] | [math]\Delta W^{(j)}[/math] | wkład do pobudzenia od i-tej współrzędnej po korekcie wag |
|---|---|---|---|---|
| 0 | 0 | 0 (dobrze) | 0 | bez zmian |
| 1 | 1 | 0 (dobrze) | 0 | bez zmian |
| 0 | 1 | -1 (odpowiedź za duża) | [math]-\eta X^{(j)}[/math] | [math](w_i - \eta x_i) x_i = w_i x_i - \eta x_i^2[/math] |
| 1 | 0 | 1 (odpowiedź za mała) | [math] \eta X^{(j)}[/math] | [math](w_i + \eta x_i) x_i = w_i x_i + \eta x_i^2[/math] |
Widać, że zawsze zmiana wagi (o ile [math]\eta[/math] nie jest zbyt duża) prowadzi w taką stronę aby po ponownym podaniu tego samego przykładu odpowiedź była bliższa pożądanej.
# -*- coding: utf-8 -*-
import numpy as np
import pylab as py
import matplotlib.animation as animation
class Perceptron(object):
"""Perceptron Rosenblatta"""
def __init__(self, w, w0):
self.w = np.array(w)
self.w0 = np.array(w0)
self.first_plot = True
def ucz(self, X, Z, eta):
delta = Z - self.licz(X)
self.w += eta*delta*X
self.w0 += eta*delta
return delta
def licz(self, X):
e = np.sum(self.w*X) + self.w0
if e >= 0:
y = 1
else:
y=0
return y
def rysuj(data):
linia.set_ydata(data)
return linia,
def licz_wynik():
global p, x, X, Z
delta=1
y = np.zeros(len(x))
#while delta > 0:
delta = 0
for j in range(len(X)):
d = p.ucz( X[j,:], Z[j], eta) # uczymy neuron j-tego elementu w ciagu uczacym
delta += np.abs(d) # sumujemy wartosci bezwzgledne bladow
y[0] = (-p.w[0]*x[0] - p.w0) / p.w[1]
y[1] = (-p.w[0]*x[1] - p.w0) / p.w[1]
print 'zla klasyfikacja ' +str(delta) +' na '+ str(len(Z)) + ' punktow '
yield y
p = Perceptron(w = [0.1, 0.6], w0 = -0.4 )
eta=0.1
X=np.array([[1, 1], [3, 3],[4,1],[2, 3], [3, 4], [1.2, 3.2]])
Z=np.array([1, 1,1, 0, 0, 0, ])
xmin=-5
xmax=5
red = np.where( Z>0 )
blue = np.where( Z<=0)
fig1 = py.figure(1)
py.plot(X[blue,0], X[blue,1],'bo' , X[red, 0], X[red,1] ,'ro')
py.xlim([xmin-2, xmax+2])
py.ylim([0-2,5+2])
x = np.array([xmin, xmax])
y = (-p.w[0]*x - p.w0) / p.w[1]
linia, = py.plot(x,y)
line_ani = animation.FuncAnimation(fig1, rysuj, licz_wynik, interval=100)#, blit=True,repeat=False)
py.show()
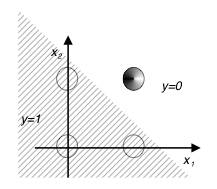
Ograniczenia perceptronu prostego
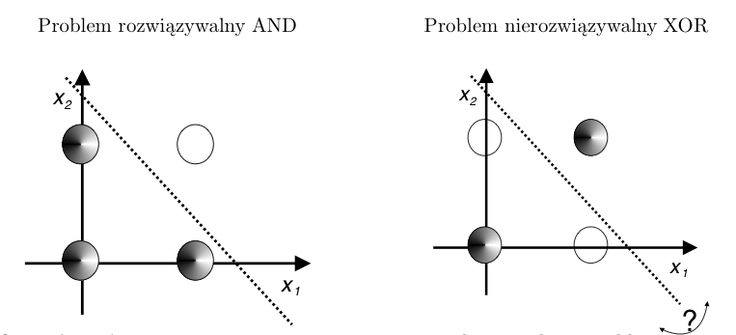
Ograniczeniem perceptronu prostego jest fakt, że za jego pomocą można rozwiązać tylko problemy separowalne liniowo. Co to oznacza zobaczmy na poniższym przykładzie:
Nowe możliwości: wielowarstwowe sieci perceptronów prostych
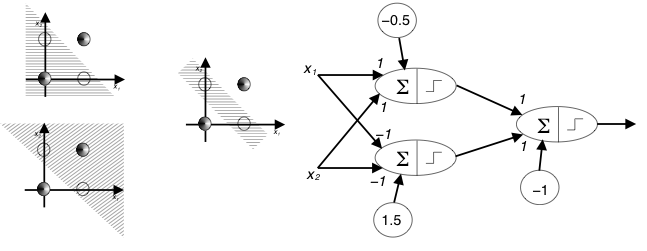
Co dwie warstwy neuronów nieliniowych to nie jedna :-) Jedna warstwa perceptronów prostych na swoim wyjściu prezentuje zestaw podziałów przestrzeni hiperpłaszczyznami - każdy neuron jeden podział.
- Co się stanie jeśli wyjście tej warstwy wpuścimy na wejście następnej warstwy?
Problem znalezienia wag w ogólności nie jest tu prosty. Dla XOR można go zapisać następująco:
- [math] f \left([v_1\; v_2] \cdot f\left( \left[ \begin{array}{cc} w_{11} & w_{12} \\ w_{21} & w_{22} \end{array} \right] \cdot \left[ \begin{array}{cccc} 0&1&0&1 \\ 0&0&1&1 \end{array} \right] + \left[ \begin{array}{c} w_{10}\\ w_{20} \end{array} \right] + v_3 \right) \right) = [0 \;1\; 1\; 0] [/math]