Uczenie maszynowe i sztuczne sieci neuronowe/Wykład 4: Różnice pomiędzy wersjami
| (Nie pokazano 2 pośrednich wersji utworzonych przez tego samego użytkownika) | |||
| Linia 1: | Linia 1: | ||
| + | [[Uczenie_maszynowe_i_sztuczne_sieci_neuronowe|powrót]] | ||
=Formy nieliniowości= | =Formy nieliniowości= | ||
Na poprzednich wykładach zajmowaliśmy się: | Na poprzednich wykładach zajmowaliśmy się: | ||
| Linia 27: | Linia 28: | ||
: <math>J(w) = \frac{1}{2} \sum_{j=1}^N\left(z^{(j)}- y^{(j)} \right)^2 = \sum_{j=1}^N J^{(j)}(w)</math> | : <math>J(w) = \frac{1}{2} \sum_{j=1}^N\left(z^{(j)}- y^{(j)} \right)^2 = \sum_{j=1}^N J^{(j)}(w)</math> | ||
gdzie: | gdzie: | ||
| − | :<math>y^{(j)} = f\left(e^{(j)}\right) = f \left( \sum_{i=0}^n w_i | + | :<math>y^{(j)} = f\left(e^{(j)}\right) = f \left( \sum_{i=0}^n w_i x_i^{(j)}\right)</math> |
zaś | zaś | ||
:<math>J^{(j)}(w) = \frac{1}{2} \left( z^{(j)} -y^{(j)}\right)^2 </math> | :<math>J^{(j)}(w) = \frac{1}{2} \left( z^{(j)} -y^{(j)}\right)^2 </math> | ||
| Linia 46: | Linia 47: | ||
gdzie wprowadziliśmy: | gdzie wprowadziliśmy: | ||
:<math>\delta^{(j)} = \frac{df(e)}{de^{(j)}} \left( z^{(j)}- y^{(j)}\right)</math> | :<math>\delta^{(j)} = \frac{df(e)}{de^{(j)}} \left( z^{(j)}- y^{(j)}\right)</math> | ||
| − | |||
==Uczenie nieliniowej sieci: Jak znaleźć błąd dla warstwy ukrytej?== | ==Uczenie nieliniowej sieci: Jak znaleźć błąd dla warstwy ukrytej?== | ||
| Linia 68: | Linia 68: | ||
Jednostka wyjściowa, ''n'' − ta, otrzymuje zatem sygnał: | Jednostka wyjściowa, ''n'' − ta, otrzymuje zatem sygnał: | ||
| − | <math> e_n^{(j)} = \sum_{i \in Wyj} W_i^{n(j)}V_i^{(j)} = \sum_{i \in Wyj} | + | :<math> e_n^{(j)} = \sum_{i \in Wyj} W_i^{n(j)}V_i^{(j)} = \sum_{i \in Wyj} |
W_i^{n(j)}f\left(\sum_{i \in U} w_i^{k(j)}x_i^{(j)}\right) | W_i^{n(j)}f\left(\sum_{i \in U} w_i^{k(j)}x_i^{(j)}\right) | ||
</math> | </math> | ||
| − | (gdzie: <math>Wyj</math> — indeksy wejść warstwy wyjściowej, '''uwaga''': <math>e_n^{(j)} \ne e_k^{(j)}</math> dla <math> n \ne k </math> !) | + | :(gdzie: <math>Wyj</math> — indeksy wejść warstwy wyjściowej, '''uwaga''': <math>e_n^{(j)} \ne e_k^{(j)}</math> dla <math> n \ne k </math> !) |
i wytwarza sygnał wyjściowy: | i wytwarza sygnał wyjściowy: | ||
:<math>y_n^{(j)} = f\left(e_n^{(j)}\right) = f\left(\sum_{i \in Wyj} W_i^{n(j)} f\left(\sum_{i \in U} w_i^{k(j)}x_i^{(j)}\right)\right) | :<math>y_n^{(j)} = f\left(e_n^{(j)}\right) = f\left(\sum_{i \in Wyj} W_i^{n(j)} f\left(\sum_{i \in U} w_i^{k(j)}x_i^{(j)}\right)\right) | ||
Aktualna wersja na dzień 15:41, 29 mar 2019
Spis treści
Formy nieliniowości
Na poprzednich wykładach zajmowaliśmy się:
- sieciami liniowymi: łatwo można dla nich sformułować i udowodnić zbieżność gradientowej reguły uczenia. Niestety miały one ograniczenie do reprezentowania odwzorowań liniowych.
- perceptornem Rosenblatta: łatwo można było wyprowadzić dla niego regułę uczenia, wnosił nową jakość- podział przestrzeni wejściowej na rozłączne obszary decyzyjne, składanie sieci wielowarstwowych wprowadza nową jakość (możliwość konstruowania dowolnych podziałów przestrzeni wejściowej ) ale:
- dla jednej warstwy można rozwiązywać tylko problemy separowalne liniowo
- dla większej ilości warstw brak jest reguły uczenia
Problem z regułą uczenia perceptronu Rosenblatta bierze się z tego, że nie można do niej wykorzystać metod spadku gradientowego, ze względu na występującą w nim nieciągłość.
Okazuje się, że w wielu przypadkach dobrze sprawdzają się następujące dwie funkcje sigmoidalne:
- funkcja logistyczna:
- [math]y = \frac{1}{1+\exp(-\beta e)} [/math]
- * pochodna: [math]\frac{dy}{de} = \beta y (1-y)[/math]
- * zbiór wartości otwarty:[math]y \in (0,1)[/math]
- tangens hiperboliczny
- [math]y = \tgh(\beta e) = \frac{\exp(\beta e)-\exp(-\beta e)}{\exp(\beta e) + \exp(-\beta e)} [/math]
- * pochodna :[math]\frac{d y }{d e} = \beta (1+y)(1-y)[/math]
- * zbiór wartości [math]y \in (-1,1)[/math]
We wszystkich powyższych wzorach [math]\beta[/math] to parametr odpowiadający za stromość sigmoidy, zaś [math]e[/math] to pobudzenie neuronu.
Uczenie
Pojedynczy neuron: reguła delta
Podobnie jak dla wszystkich omawianych dotychczas sieci celem uczenia neuronu nieliniowego jest taki dobór jego wag, aby zminimalizować błąd średnio-kwadratowy popełniany na ciągu uczącym. Niech ciąg uczący będzie:
- [math]\left\{ \left(X^{(j)}, z^{(j)}\right)\right\}_{j = 1,\dots,N} [/math]
Funkcja błędu to:
- [math]J(w) = \frac{1}{2} \sum_{j=1}^N\left(z^{(j)}- y^{(j)} \right)^2 = \sum_{j=1}^N J^{(j)}(w)[/math]
gdzie:
- [math]y^{(j)} = f\left(e^{(j)}\right) = f \left( \sum_{i=0}^n w_i x_i^{(j)}\right)[/math]
zaś
- [math]J^{(j)}(w) = \frac{1}{2} \left( z^{(j)} -y^{(j)}\right)^2 [/math]
podobnie jak w przypadku regresji liniowej chcemy zmieniać wag w kierunku przeciwnym do kierunku gradientu funkcji kosztu, tzn. po prezentacji j = 1 przykładu i-ta waga zmienia się tak:
- [math]w_i^{(j+1)} - w_i^{(j)} = \Delta w_i^{(j)} = -\eta \frac{\partial J^{(j)} }{\partial w_i} = -\eta \frac{\partial J^{(j)} }{\partial y^{(j)}} \frac{\partial y^{(j)}}{\partial w_i} = - \eta \frac{\partial J^{(j)} }{\partial y^{(j)}} \frac{\partial y^{(j)}}{\partial e} \frac{\partial e}{\partial w_i} [/math]
łatwo zauważyć, że:
- [math]\frac{\partial J^{(j)} }{\partial y^{(j)}} = - \left( z^{(j)} -y^{(j)}\right) [/math]
oraz, że:
- [math] \frac{\partial e}{\partial w_i} = x_j^{(j)}[/math]
natomiast:
- [math]\frac{\partial y^{(j)}}{\partial e^{(j)}} = \frac{d f(e)}{de^{(j)}} [/math]
Łącząc te wszystkie spostrzeżenia otrzymujemy:
- [math] \Delta w_i^{(j)} = \eta \frac{df(e)}{d e^{(j)}}\left(z^{(j)} - y^{(j)}\right)x_i^{(j)} = \eta \delta^{(j)}x_i^{(j)}[/math]
gdzie wprowadziliśmy:
- [math]\delta^{(j)} = \frac{df(e)}{de^{(j)}} \left( z^{(j)}- y^{(j)}\right)[/math]
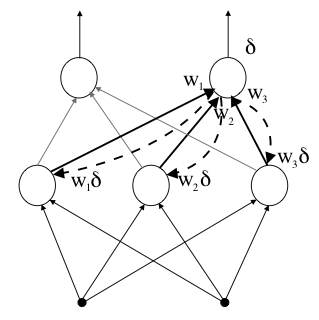
Uczenie nieliniowej sieci: Jak znaleźć błąd dla warstwy ukrytej?
- Pomysł
błąd [math]\delta_m^{(j)}[/math] występujący w j − tym kroku uczenia na neuronie m rzutujemy wstecz do wszystkich neuronów, które stanowią wejście dla neuronu m − tego. Rzutując, mnożymy błąd przez ten sam współczynnik wagowy, który w czasie propagacji w przód ważył wejście.
- Dlaczego?
- Uzasadnienie intuicyjne
- Jeśli neuron warstwy ukrytej przyczynił się do powstania błędu na neuronie warstwy wyjściowej rzutując w przód przez dużą wagę, to trzeba mu zwrócić informację o błędzie proporcjonalnie do tej wagi.
- Uzasadnienie formalne
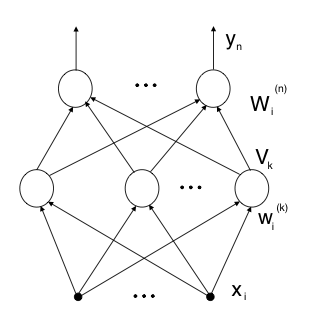
Reguła ta wynika wprost z gradientowej metody minimalizacji funkcji błędu. Rozważmy sieć dwuwarstwową. Dla wzorca j − tego k − ta jednostka ukryta otrzymuje pobudzenie:
- [math]e_k^{(j)} = \sum_{i \in U}w_i^{k{(j)}}x_i^{(j)}[/math]
gdzie: [math] U [/math] - indeksy wejść warstwy ukrytej, [math]w_i^{k{(j)}}[/math] - i-ta waga k-tej jednostki w j-tym kroku uczenia. Jednostka ta wytwarza sygnał wyjściowy:
- [math]V_k^{(j)} = f\left( e_k ^{(j)}\right) = f\left(\sum_{i \in U} w_i^{k(j)} x_i^{(j)}\right) [/math]
Jednostka wyjściowa, n − ta, otrzymuje zatem sygnał:
- [math] e_n^{(j)} = \sum_{i \in Wyj} W_i^{n(j)}V_i^{(j)} = \sum_{i \in Wyj} W_i^{n(j)}f\left(\sum_{i \in U} w_i^{k(j)}x_i^{(j)}\right) [/math]
- (gdzie: [math]Wyj[/math] — indeksy wejść warstwy wyjściowej, uwaga: [math]e_n^{(j)} \ne e_k^{(j)}[/math] dla [math] n \ne k [/math] !)
i wytwarza sygnał wyjściowy:
- [math]y_n^{(j)} = f\left(e_n^{(j)}\right) = f\left(\sum_{i \in Wyj} W_i^{n(j)} f\left(\sum_{i \in U} w_i^{k(j)}x_i^{(j)}\right)\right) [/math]
Miara błędu wygląda tak:
- [math]J(\mathbf{w}) = \frac{1}{2}\sum_{n,j}\left(z_n^{(j)} - y_n{(j)}\right)^2 = \frac{1}{2}\sum_{n,j} \left(z_n^{(j)} - f\left( \sum_{i \in Wyj} W_i^{n(j)}f\left(\sum_{i \in U}w_i^{k(j)}x_i^{(j)}\right)\right) \right)^2 [/math]
i jest ciągłą i różniczkowalną funkcją wszystkich wag, możemy więc ją minimalizować zmieniając wagi w kierunku przeciwnym do gradientu ([math]\mathbf{w}[/math] to wszystkie wagi zarówno w jak i W ).
Dla warstwy wyjściowej otrzymujemy:
- [math] \Delta W_i^{n(j)} = -\eta \frac{\partial J^{(j)}}{\partial W_i^{n}} = \eta \left( z_n^{(j)} - y_n^{(j)}\right) \frac{df(e_n^{(j)})}{de} V_k^{(j)} = \eta \delta^{(j)} V_k^{(j)} [/math]
gdzie oznaczyliśmy: [math]\delta_n^{(j)} = \left( z_n^{(j)} - y_n^{(j)}\right) \frac{df(e_n^{(j)})}{de}[/math]
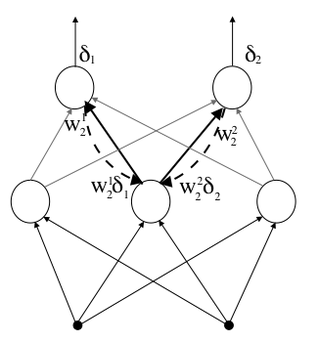
Dla warstwy ukrytej otrzymujemy:
- [math]\Delta w_i^{k(j)} = -\eta \frac{\partial J^{(j)}}{\partial w_i^k} = -\eta \frac{\partial J^{(j)}}{\partial V_k }\frac{\partial V_k^{(j)}}{\partial w_i^k} =[/math]
- [math] = \eta \sum_n \left(z_n^{(j)} - y_n^{(j)}\right) \frac{df(e_n^{(j)})}{d e_n}W_i^n \frac{df(e_k^{(j)})}{de_k} x_i^{(j)} =[/math]
- [math]=\eta \sum_n \delta_n^{(j)}W_i^n \frac{df(e_k^{(j)})}{de_k}x_i^{(j)} =[/math]
- [math] =\eta \delta_k^{(j)} x_i^{(j)} [/math]
przy czym zdefiniowaliśmy:
- [math]\delta_k^{(j)} = \frac{df(e_k^{(j)}) }{d e_k} \sum_n W_i^n \delta_n^{(j)}[/math]
Widać, że wzór na zmianę wag, czy to warstwy wejściowej, czy ukrytej ma tę samą postać, różni się jedynie definicją [math] \delta[/math]. Dla warstw ukrytych błąd jest sumą ważoną (wagami połączeń do przodu) błędów popełnionych w wyższej warstwie.
Regułę tą można udowodnić dla dowolnej ilości warstw stosując odpowiednią ilość razy regułę łańcuchową.
Problemy uczenia metodą wstecznej propagacji błędu
- Minima lokalne funkcji kosztu. W odróżnieniu od funkcji kosztu dla problemu sieci liniowych w przypadku sieci nieliniowych funkcja kosztu ma zazwyczaj wiele lokalnych minimów. Algorytm wstecznej propagacji błędu jako algorytm spadku gradientowego nie jest odporny na ich występowanie.
- Generalizacja: Uczenie z wykorzystaniem tylko jednego ciągu uczącego i reguły wstecznej propagacji błędu może prowadzić do problemów z generalizacją, czyli wynikami działania sieci na danych nie występujących w ciągu uczącym.
Klasyczne przykłady zastosowań
- XOR
- rozwiązanie metodą wstecznej propagacji dla jednostek sigmoidalnych — jednostki są sterowane w stronę wysycenia. Czas uczenia jest bardzo długi: setki epok prezentacji całego zbioru treningowego.
- Koder
- Dwuwarstwowa sieć o N wejściach, N wyjściach i M neuronach w warstwie ukrytej (M < N). Chcemy uzyskać autoasocjację czyli X(j) = Y (j).
- Praktyczne zastosowanie — kompresja np. obrazów.
- Teoretyczne — wyznaczanie możliwości sieci — problem łatwo można skalować i zmieniać jego trudność przez zmianę M/N.
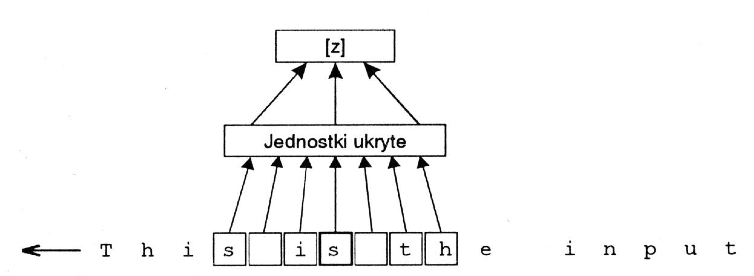
- NETtalk
- Klasyczna praca (Sejnowski i Rosenberg 1987,Complex Systems 1, 145–168): generacja ciągu fonemów z angielskiego tekstu pisanego.
- Architektura: 7 × 29 wejść kodujących 7 kolejnych liter, 80 jednostek ukrytych, 26 jednostek wyjściowych kodujacych fonemy.
- Zbiór uczący: 1024 słowa podawane w postaci par (litera,fonem)
- Efekty: po 10 epokach zrozumiała wymowa, po 50 — 95% odtwarzania zbioru treningowego, 78% na ciągłym tekście źródłowym. Porównanie stanowi system algorytmiczny DEC-talk (jest lepszy)
- Struktura drugorzędowa białka
- (Quian, Sejnowski (1988), Journal of Molecural Biology 202, 865–884).
- Wejście — ruchome okno z 13 aminokwasów.
- Na wyjściu odczytujemy prognozę struktury środkowej części okna jako spirali α, arkusza β lub innej struktury.
- Efekt: na nowym zbiorze danych dokładność predykcji 62% (w porównaniu do konkurencyjnej metody 53%)
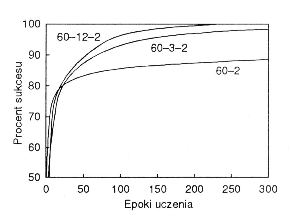
- Rozpoznawanie celów sonarowych
- (Gorman i Sejnowski (1988) Neural Network 1, 75–89) Problem: rozróżnianie sygnałów sonarowych odbitych albo od skał albo od metalowych cylindrów leżących na dnie zatoki.
- Preprocessing: transformanta Fouriera
- Architektura: 60 jednostek wejściowych i 2 wyjściowe, liczba jednostek ukrytych od 0 –24,
- Na nowych danych (generalizacja ) dla 12 jednostek ukrytych ∼ 85%; poprawa jakości do ∼ 90% po staranniejszym wybraniu zbioru treningowego.
- Kierowanie samochodem (Pomerlau, 1989)
- Sygnał wejściowy — obraz z kamery video 30 × 32 piksle umocowanej na dachu oraz obraz 8 × 32 piksle z dalmierza kodującego odległość w skali szarości,
- warstwa ukryta 29 jednostek, wyjście 45 jednostek ułożonych w linię (środkowa jednostka kodowała jazdę na wprost, boczne — kąt skrętu odpowiednio w lewo lub w prawo).
- Zbiór treningowy: 1200 symulowanych fragmentów drogi. Uczenie: około 40 powtórzeń każdego ze wzorców.
- Efekt: sieć mogła prowadzić samochód z prędkością około 5 km/h po drodze przez zalesiony obszar wokół kampusu Carrengie-Mellon.
Ograniczenie prędkości: moc obliczeniowa komputera — sieć symulowana była na komputerze Sun-3 (metody algorytmiczne dawały prędkość o połowę mniejszą) [kierowania samochodem (czas 3:25-8:38)]
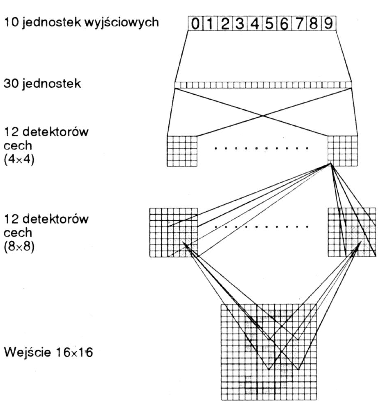
- Rozpoznawanie ręcznie pisanych kodów pocztowych(Le Cun 1989, Neural Computaion 1 541–551)
- Preprocessing: rozdzielenie kodów na po jedyncze cyfry, wyskalowanie do standardowych rozmiarów i skwantowanie na tablicę piksli 16 × 16.
- W całej sieci było w sumie 1256 jednostek i 9700 niezależnych parametrów.
- Nauka na zbiorze 7300 cyfr i test na 2000 cyfr.
- Wynik: 1% błędów dla zbioru uczącego i 5% dla testowego. Po dopuszceniu odpowiedzi ”nie wiem” błąd na zbiorze testowym 1%, ale odrzucone było 12% cyfr. Dalszą poprawę generalizacji uzyskano po usunięciu niepotrzebnych wag (99% trafności przy 9% odrzutów)