Laboratorium EEG/CSP

Laboratorium_EEG/BSS

Ślepa separacja źródeł

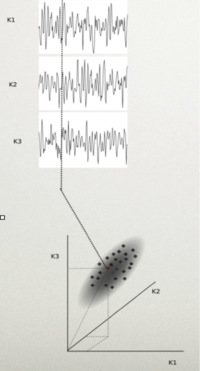
Rozważmy N-kanałowy sygnał EEG. Próbkę tego sygnału możemy przedstawić jako punkt w przestrzeni rozpiętej przez osie, z których każda reprezentuje wartość potencjału w jednym kanale. Cały sygnał tworzy w tej przestrzeni chmurę punktów. Rozciągłość tej chmury w danym kierunku mówi nam o wariancji (zmienności) sygnału w tym kierunku.

Taki zbiór punktów wygodniej jest analizować w układzie współrzędnych zgodnym z osiami głównymi macierzy kowariancji. W dalszej części rozważań założymy, że te przestrzenie, w których rozważamy sygnały są przestrzeniami wektorowymi, a pojedyncze próbki wielokanałowego sygnału są wektorami.

Filtry przestrzenne i ślepa separacja źródeł

Sygnał EEG jest superpozycją aktywności elektrycznej wielu źródeł. Jak można estymować aktywność samych źródeł?

Niech:

[math]s(t)[/math] - aktywność niezależnych źródeł,

[math]x(t)[/math] mierzony sygnał

[math]A[/math] macierz przejścia taka, że:

[math]x(t) = A s(t)[/math] (*)

[math]s(t) = A^{-1}x(t) = P x(t)[/math]

Macierz kowariancji dla sygnałów [math]x(t)[/math] estymujemy tak:

[math] C_x = E[x(t)x(t)^T][/math]

Podstawiając (*) mamy:

[math] C_x = E[x x^T] = E[As(As)^T] = A E[s s^T] A^T = A C_s A^T[/math]

Z założenia, że źródła są niezależne wynika, że macierz [math]C_s[/math] jest diagonalna. Przekształcając powyższe równanie możemy zapisać:

[math]A^{-1} C_x (A^T)^{-1} = P C_x P^T = C_s[/math]

Odwzorowanie [math]P = A^{-1}[/math] diagonalizuje macierz [math]C_x[/math].

Powyższe rozumowanie jest słuszne w przypadku gdy mamy do czynienia z sygnałem stacjonarnym, tzn. jego macierz kowariancji jest niezależna od czasu, czyli przez cały czas aktywna jest ta sama konfiguracja źródeł niezależnych. W przypadku gdy tak nie jest to konstrukcję filtra przestrzennego można oprzeć o jednoczesną diagonalizację macierzy kowariancji odpowiadających różnym stanom osoby badanej.

Common Spatial Pattern

Koncepcja

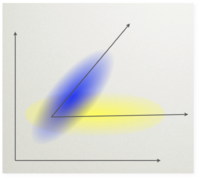
Dla ustalenia uwagi możemy myśleć o eksperymencie wywołującym potencjał P300. Mamy w nim dwie sytuacje eksperymentalne. Oznaczmy ([math]T[/math] - target) próby, w których pojawił się oczekiwany bodziec, zaś ([math]NT[/math] - non-target) gdy pojawił się bodziec standardowy. Chcielibyśmy znaleźć taki montaż, czyli taką kombinację liniową kanałów, które maksymalizuje stosunek mocy (wariancji) sygnałów rejestrowanych w dwóch rożnych warunkach eksperymentalnych.

Formalizm

Metoda ta polega na znalezieniu takiego kierunku [math]w[/math] w przestrzeni sygnałów, że sygnał z warunku [math]T[/math] rzutowany na ten kierunek ma dużą wariancje a sygnał z warunku [math]NT[/math] ma wariancję małą.

Rzutowanie sygnału [math]x(t)[/math] na kierunek [math]w[/math] odbywa się przez policzenie iloczynu skalarnego dla każdej chwili czasu [math]t[/math]:

[math] s_w(t) = w^T x(t)[/math]

Wariancja tego rzutowanego sygnału to:

[math] \mathrm{var}(s_w) = E[s_w s_w^T] = E[ w^T x (w^T x)^T] = w^T E[x x^T] w = w^T C_x w [/math]

Zatem znalezienie właściwego kierunku rzutowania można wyrazić jako szukanie maksimum wyrażenia [math] J(w) [/math](jest to tzw. iloraz Rayleigh'a):

[math]J(w) = \frac{w^T C_T w}{w^T C_{NT} w} [/math]

Ekstremum tego ilorazu można znaleźć poprzez policzenie gradientu [math]J(w)[/math] i przyrównanie go do zera:

[math] \nabla J(w) = \frac{ 1 C_{T} w+w^T C_{T} 1}{w^T C_{NT} w}-\frac{w^T C_{T} w\left( 1 C_{NT} w+w^T C_{NT} 1\right)}{\left(w^T C_{NT} w\right)^2}[/math]

ponieważ macierze kowariancji są symetryczne

[math]\nabla J(w) = \frac{ 1}{w^T C_{NT} w}\left[ C_{T} w+ C_{T}w -\frac{w^T C_{T} w}{w^T C_{NT} w} \left( C_{NT} w+ C_{NT}w \right) \right][/math]

[math]= \frac{ 2}{w^T C_{NT} w}\left[ C_{T}w -\frac{w^T C_{T} w}{w^T C_{NT} w} C_{NT} w \right][/math]

Przyrównując to wyrażenie do zera dostajemy:

[math] C_{T}w =\frac{w^T C_{T} w}{w^T C_{NT} w} C_{NT} w [/math]

We wzorze tym liczba [math]\lambda=\frac{w^T C_{T} w}{w^T C_{NT} w}[/math] spełniająca to równanie jest uogólnioną wartością własną, wtedy [math]w[/math] jest uogólnionym wektorem własnym odpowiadającym tej wartości.

Aby znaleźć [math] \lambda[/math] i [math]w[/math] należy rozwiązać zagadnienie własne. W Matlabie możemy w tym celu wykorzystać funkcję eig

Ćwiczenie symulacyjne

% symulowany eksperyment składa się z sinusoidy udającej alfę spoczynkową i
% funkcji Gaussa udającego potencjał wywołany
% źródła te są symulowane niezależnie a potem mieszane przez macierz L
% symulujemy źródła
% s1 - symuluje alfę
% s2 - symuluje "potencjał wywołany" (ERP)

%ustawiamy parametry do symulacji sygnałów
Fs = 100;
T = 1;
t = 0:1/Fs:T-1/Fs;
N_rep = 100;
N_chan = 2;
s = zeros(N_rep,N_chan, length(t));
X = zeros(N_rep,N_chan, length(t));

% filtr przestrzenny - z takimi wagami trzeba wziąść kanały EEG aby odzyskać sygnały źródłowe
P = [1 2
    1.5 1.3]; 


% topografie - z takimi wagami źródła dokładają się do poszczególnych elektrod
A = P^(-1); 


for r =1:N_rep % tworzymy kolejne realizacje "eksperymentu"
    s1 = sin(2*pi*11*t +pi/2+ 0*2*pi*rand())+ 0.02*randn(size(t));  % źródło alfa
    s2 = exp(-((t-0.8)/0.05).^2)+ 0.01*randn(size(t));              % źródło ERP
       
    s(r,1,:) = s1;
    s(r,2,:) = s2;
    tmp = squeeze(s(r,:,:));
    n = 0*randn(size(tmp));
    X(r,:,:) = A*tmp +n; % rzutujemy sygnały źródłowe na elektrody s -> x
    
end

% wycinamy warunki 
% baseline_ind   to indeksy pierwszej połowy każdego powtórzenia "baseline"
% ERP_ind        to indeksy drugiej połowy każdego powtórzenia zawierająca "ERP"
baseline_ind = find(t<0.5);
ERP_ind = find(t>=0.5);

x_baseline_kan_1 = X(:,1,baseline_ind);
x_baseline_kan_2 = X(:,2,baseline_ind);

x_ERP_kan_1 = X(:,1,ERP_ind);
x_ERP_kan_2 = X(:,2,ERP_ind);



% liczymy średnie macierze kowariancji:
R_E = zeros(N_chan,N_chan);
R_B = zeros(N_chan,N_chan);
for r =1:N_rep
    B = squeeze(X(r,:,baseline_ind)); 
    tmp =cov(B');
    R_B = R_B + tmp./trace(tmp);%B*B' ;
 
    E = squeeze(X(r,:,ERP_ind));
    tmp = cov(E');
    R_E = R_E + tmp./trace(tmp);%E*E' ;
end

R_B = R_B/N_rep;
R_E = R_E/N_rep;

% rozwiązujemy uogólnione zagadnienie własne
[W,Lambda]=eig(R_E,R_B); % możliwa jest też optymalizacja wzg. średniej macierzy kowariancji (R_B+R_A)/2);

% odzyskujemy sygnały źródeł
for r =1:N_rep
    S(r,:,:) = W'*squeeze(X(r,:,:));
end

% pobieramy wycinki odpowiadające obu częściom eksperymentu z estymowanych
% źródeł
s_baseline_estymowany_kan1 = squeeze(  S(:,1,baseline_ind));
s_baseline_estymowany_kan2 = squeeze(  S(:,2,baseline_ind));

s_ERP_estymowany_kan1 = squeeze(S(:,1,ERP_ind));
s_ERP_estymowany_kan2 = squeeze(S(:,2,ERP_ind));

%%%%%%%%%%%%%% Ilustracje %%%%%%%%%%%%%%%%%%%%%%%
% ilustracja sygnałów mierzonych
figure(1);clf
subplot(2,2,1);
    plot(t(baseline_ind),(squeeze(X(:,1,baseline_ind)))','b'); hold on
    plot(t(ERP_ind),(squeeze(  X(:,1,ERP_ind)))','r'); hold off
    xlabel('elektroda 1')
    title('ilustracja sytuacji pomiarowej -\newline znane są potencjały na elektrodach w dwóch warunkach eksperymentalnych')
subplot(2,2,3);
    plot(t(baseline_ind),(squeeze(X(:,1,baseline_ind)))','b'); hold on
    plot(t(ERP_ind),(squeeze(  X(:,2,ERP_ind)))','r'); hold off
    xlabel('elektroda 2')
subplot(1,2,2)
    plot(x_baseline_kan_1(:),x_baseline_kan_2(:),'b.');
    hold on
    plot(x_ERP_kan_1(:),x_ERP_kan_2(:),'r.');
    xlim([-2,2])
    ylim([-2,2])
    axis equal
    
    % wektor własny odpowiadający największej wartości własnej jest
    % kierunkiem najbardziej różnicującym warunki eksperymentalne
    disp('wartości własne znajdują się na przekątnej macierzy Lambda')
    disp(Lambda)
    % rysujemy wersory jednostkowe w kierunkach wektorów własnych
    w1 = W(:,1); 
    w1 = w1/norm(w1);
    w2 = W(:,2); 
    w2 = w2/norm(w2);
    line([0, w1(1) ],[0,w1(2)],'Color',[0,0.3,0])
    text(w1(1),w1(2),'wektor własny 1')
    line([0, w2(1) ],[0,w2(2)],'Color',[1,0,1])
    text(w2(1),w2(2),'wektor własny 2')
    
    
    xlabel('Amplituda na elektrodzie 1')
    ylabel('Amplituda na elektrodzie 2')   
    legend('baseline','ERP')

% Ilustracja estymowanych źródeł
figure(2);clf
subplot(2,2,1);
    plot(t(baseline_ind),(squeeze(S(:,1,baseline_ind)))','b');hold on
    plot(t(ERP_ind),(squeeze(S(:,1,ERP_ind)))','r');hold off
    xlabel('estymowane zrodlo  1')
    title('ilustracja estymacji -\newline estymowane są potencjały źródeł w dwóch warunkach eksperymentalnych')    
subplot(2,2,3);
    plot(t(baseline_ind),(squeeze(S(:,2,baseline_ind)))','b');hold on
    plot(t(ERP_ind),(squeeze(S(:,2,ERP_ind)))','r');hold off
    xlabel('estymowane zrodlo  2');
subplot(1,2,2)
    plot(s_baseline_estymowany_kan1(:),s_baseline_estymowany_kan2(:),'b.');
    hold on
    plot(s_ERP_estymowany_kan1(:),s_ERP_estymowany_kan2(:),'r.');   
    
    xlabel('Amplituda estym. źródła 1')
    ylabel('Amplituda estym. źródła 2')   
    legend('baseline','ERP')

Zastosowanie filtra CSP do detekcji potencjału P300

Eksperyment

Przygotowanie do badania:

• założyć czepek z elektrodami w systemie 10-20;
• elektrody referencyjne: M1 i M2;
• elektroda GND w pozycji AFz.

Przygotowanie scenariuszy obci

• w terminalu uruchomić obci srv;
• w terminalu uruchomić obci_gui --preset brain2013;
• w interfejsie GUI zapisujemy scenariusze do własnego katalogu np „P300”
  • „P-Brain2013 Signal (with ID)” jako np. „Sygnal”
  • „P-Brain2013 Calibration p300” jako „kalibracjaP300”
  • „P-Brain 2013 p300” jako „Labirynt”
• w przeglądarce plików otwórz katalog ~/.obci/scenarios/P300. Powinien on zawierać pliki: Sygnal.ini, kalibracjaP300.ini, Labirynt.ini oraz katalogi Sygnal_configs, kalibracjaP300_configs, Labirynt_configs.
• edytujemy parametry peerów.
  • z katalogu ~/.obci/scenarios/P300/Sygnal_configs kopiujemy plik amplifier.ini do katalogu ~/.obci/scenarios/P300 jako global_amplifier.ini. To pozwoli nam zmieniać ustawienia wzmacniacza dla wszystkich scenariuszy jednocześnie.
  • w naszych scenariuszach zapisanych w plikach Sygnal.ini, kalibracjaP300.ini, Labirynt.ini podmieniamy ścieżkę config = w sekcji [peers.amplifier] tak, aby pokazywała na ten skopiowany plik global_amplifier.ini
  • w tym pliku global_amplifier.ini podmieniamy linijki (tak aby były to listy faktycznie wykorzystywanych kanałów) z:
    • active_channels
    • channel_names
  • dodajemy też linijkę: sampling_rate = 256
• wchodzimy po kolei do katalogów: Sygnal_configs, kalibracjaP300_configs, Labirynt_configs i odnajdujemy plik switch_backup.ini. W tym pliku ustawiamy parametr new_scenario na pusty. To spowoduje, że scenariusze te nie będą uruchamiać kolejnych scenariuszy po zakończeniu działania.
  • edytujemy plik ~/.obci/scenarios/P300/kalibracjaP300_configs/clasifier.ini
    • zmieniamy linię

ignore_channels = DriverSaw;AmpSaw;PO7;PO8

na

ignore_channels = DriverSaw;AmpSaw;A1;A2

• oraz linię:

montage_channels = PO7;PO8

na

montage_channels = A1;A2

Przeprowadzenie badania:

1. Uruchom scenariusz „Sygnał”.
2. Tworzy on w katalogu domowym plik o nazwie file_id_name.
3. Uruchamiamy Svaroga z terminala poleceniem svarog. W zakładce sygnały on-line odnajdujemy nazwę naszego scenariusza „Sygnal”. Podłączamy się do niego i poprawiamy ewentualnie źle kontaktujące elektrody.
4. Jak już jesteśmy zadowoleni z jakości sygnału to zatrzymujemy scenariusz „Sygnal” w obci.
5. W pliku file_id_name znajduje się string, który stanowi rdzeń do tworzenia nazw plików, z których korzystają nasze scenariusze. Proszę zmienić ten string np. na: test1.
6. Uruchamiamy scenariusz „kalibracjaP300”. Badany będzie oglądał interfejs z trzema literami A B C migającymi w losowej kolejności. Zadaniem jest zliczanie mignięć litery B.
7. Po zakończeniu kalibracji uruchamiamy scenariusz „Labirynt”.
8. Danych z kalibracji potrzebować będziemy kilka zestawów. Proszę powtórzyć kilkukrotnie scenariusz „kalibracjaP300”. Przed każdym uruchomieniem trzeba zmienić string w pliku file_id_name np. na test??? gdzie ??? oznacza kolejne numery.

Analiza wstępna

• Wczytać dane kalibracyjne do Matlaba i pociąć je na realizacje typu T — „target” (związane z wystąpieniami litery „B”) i NT — „non-target” (pozostałe litery) o długości −200 do +800 ms wokół triggerów. Dla każdej realizacji odjąć trend liniowy.
• Sygnał zmontować wzgl. „połączonych uszu” i wyświetlić średnie przebiegi dla warunku T i NT w układzie topograficznym — wykorzystać w tym celu funkcję topoplot z pakietu Eeglab.

Poniżej zaprezentowany jest przykładowy skrypt do cięcia danych wokół znaczników. Działa on z plikami zawartymi w archiwum:

Plik:KalibracjaP300.tar.gz

Korzysta z funkcji pomocniczych dostępnych w dystrybucji obci w katalogu

/usr/share/openbci/analysis/matlab_obci_signal_processing

Openbci można pobrać z https://github.com/BrainTech/openbci

% ustalamy nzawy plików z danymi
nazwaPliku = 'p_6301423_calibration_p300.obci';
nameOfXMLFile = strcat(nazwaPliku,'.xml');
nameOfTagFile = strcat(nazwaPliku,'.tag'); %tagi = znaczniki zdarzeń
namesOfDataFiles = strcat(nazwaPliku,'.raw');

% inicjujemy obiekt rm
rm = ReadManager(nameOfXMLFile,namesOfDataFiles,nameOfTagFile);

% obieramy przydatne parametry i znaczniki
numberOfChannels  = rm.get_param('number_of_channels');
namesOfChannels   = rm.get_param('channels_names');
samplingFrequency = rm.get_param('sampling_frequency');
tagsStruct        = rm.get_tags();

% tworzenie list znaczników Target i NonTarget
numberOfStruct = length(tagsStruct);
targetTimeStamps = [];
NonTargetTimeStamps = [];
for structNumber = 1:numberOfStruct % iterujemy się przez tagi
    if(strcmp(tagsStruct(structNumber).name,'blink')) % szukamy tagów o nazwie 'blink'
        index = tagsStruct(structNumber).children.index; % tu jest numer pola stymulacji
        target= tagsStruct(structNumber).children.target;% tu jest numer pola na którym wyświetlany jest target
        if index == target % warunek na to, że mamy do czynienia z tagiem target
            targetTimeStamps = [targetTimeStamps tagsStruct(structNumber).start_timestamp]; %dodajemy timeStamp do listy targetów
        else
            NonTargetTimeStamps = [NonTargetTimeStamps tagsStruct(structNumber).start_timestamp];%dodajemy timeStamp do listy non-targetów
        end
        
    end
end



% pobieramy próbki
samples = double(rm.get_samples()); % konwersja na double jest potrzebna żeby dobrze funkcjonowało filtrowanie
samples=samples(1:8,:); % odrzucamy kanały, które nie mają EEG
numberOfChannels =8;

% filtrujemy dolnoprzepustowo aby odrzucić artefakty sieci i część
% artefaktów mięśniowych
[b,a] = cheby2(6,80,25 /(samplingFrequency/2),'low');
for ch = 1:numberOfChannels
    samples(ch,:)=filtfilt(b,a,samples(ch,:));
end

% montujemy dane do wspólnej średniej (common average)
M = -ones(8,8)/8;
M=M+eye(8,8)*9/8;
samples = 0.0715*M*samples;

% wycinamy dane wokół znaczników
PRE = -0.2; % czas przed tagiem w sek.
POST = 0.8; % czas po tagu w sek.
wycinek = floor(PRE*samplingFrequency:POST*samplingFrequency); % tablica ze "standardowymi" indeksami do cięcia

% pobieramy targety
TargetSignal = zeros(length(targetTimeStamps),numberOfChannels, length(wycinek)); % tablica na sygnały target
for trialNumber = 1:length(targetTimeStamps)
    trigerOnset = floor(targetTimeStamps(trialNumber)*samplingFrequency);
    tenWycinek = wycinek + trigerOnset;
    if tenWycinek(1)>0 && tenWycinek(end)<=size(samples,2) % test czy wycinek który chcemy pobrać nie wystaje poza dostępny sygnał
        tmpSignal = samples(:,tenWycinek);
        tmpSignal = detrend(tmpSignal')'; % usuwanie liniowego trendu - przy krótkich wycinkach działa lepiej niż filtrowanie górnoprzepustowe
        TargetSignal(trialNumber, :,:) = tmpSignal;
    end
end

% pobieramy non-targety
NonTargetSignal = zeros(length(NonTargetTimeStamps),numberOfChannels, length(wycinek));% tablica na sygnały non-target
for trialNumber = 1:length(NonTargetTimeStamps)
    trigerOnset = floor(NonTargetTimeStamps(trialNumber)*samplingFrequency);
    tenWycinek = wycinek + trigerOnset;
    if tenWycinek(1)>0 && tenWycinek(end)<=size(samples,2)
        tmpSignal = samples(:,tenWycinek);
        tmpSignal = detrend(tmpSignal')';
        NonTargetSignal(trialNumber, :,:) = tmpSignal;
    end
end
%
% dla ilustracji podglądamy średnie po powtórzeniach ze wszystkich targetów
% i non-targetów
plot(squeeze(mean(TargetSignal,1))','r');
hold on
plot(squeeze(mean(NonTargetSignal,1))','b')

Analiza CSP

Link do Read menager [1]

• Korzystając z danych kalibracyjnych wykonać analizę CSP wzmacniającą potencjał P300.
• Zaprezentować średnią ze wszystkich kanałów źródłowych z warunku target (jeden kolor) i non-target (inny kolor) w subplotach ułożonych w prostokątnej siatce. Zaobserwować dla którego kanału średnie różnią się najbardziej. Czy jest związek tego kanału z wartościami własnymi?

• Dla kanału najbardziej różnicującego wykonać mapki topograficzne wektorów odpowiadających:
  • filtrowi przestrzennemu
  • rzutu topograficznego źródła na elektrody.
• Do wykonania tych mapek wykorzystać funkcję topoplot z pakietu eeglab
• Zbadać powtarzalność topografii pomiędzy plikami konfiguracyjnymi.

Wybór i separacja cech

• Przedstaw na rysunkach nałożone na siebie pojedyncze realizacje z warunków target i non-target po rzutowaniu na wektor [math]w[/math] odpowiadający największej i kolejnej wartości własnej.
• Przedstaw wykresy punktowe takie, że na jednej osi jest moc sygnału odpowiadającego największej wartości własnej, a na drugiej osi kolejnej wartości własnej; jeden punkt reprezentuje jedno powtórzenie.
• Wykonaj serię wykresów jak w poprzednim punkcie dla uśrednień kolejno po 2, 4, 6, 8 i 10 realizacjach. Zaobserwuj jak zmienia się separacja w grupach target i non-target.

Filtry przestrzenne dla SSEP

Teoria

Ciekawa koncepcja filtra przestrzennego dla SSVEP zaprezentowana jest tu: http://www.eurasip.org/Proceedings/Eusipco/Eusipco2009/contents/papers/1569193209.pdf

Pokrótce można ją rozumieć podobnie do tego co robiliśmy rozważając filtry przestrzenne CSP z tym, że dla SSVEP oraz innych potencjałów wywołanych stanu ustalonego możemy skorzystać z dodatkowych informacji dotyczących poszukiwanych źródeł. Wiemy mianowicie, że powinny one oscylować z częstością bodźca, i być może jej harmonicznych.

Przyda nam się macierz [math]S[/math] zbudowana tak, że w kolejnych kolumnach znajdują się sinusy i cosinusy kolejnych częstości harmonicznych. Wektory te unormujemy, żeby miały energię równą 1. Innymi słowy macierz [math]S[/math] zbudowana jest z wersorów rozpinających przestrzeń, w której powinien znajdować się sygnał SSVEP.

W matlabie możemy taką macierz zbudować tak:

% Fs - częstość próbkowania
% numberOfSamples - długość sygnału w próbkach
% numberOfHarmonics - liczba harmonicznych, które chcemy włączyć do analizy
t = (0:1:numberOfSamples - 1)/Fs; 
S = zeros(numberOfSamples, 2*numberOfHarmonics);

for harmonicNumber = 1:numberOfHarmonics
    c = cos(2*pi*stimulationFrequency*harmonicNumber*t);
    s = sin(2*pi*stimulationFrequency*harmonicNumber*t);
    S(:,(harmonicNumber - 1)*2 + 1) = c/norm(c);
    S(:,(harmonicNumber - 1)*2 + 2) = s/norm(s);
end

Aby w badanym sygnale znaleźć składowe odpowiadające SSVEP musimy rzutować sygnał [math]X[/math] (macierz sygnałów kanały x próbki) na przestrzeń rozpiętą przez [math]S[/math]:

[math]A = X*S[/math]

Macierz [math]A[/math] zawiera współczynniki będące iloczynami skalarnymi sygnałów i wersorów. Mówią one o tym "jak duże" jest sinusa bądź cosinusa o danej częstości w pierwotnym sygnale. Komponenty SSVEP zawarte w sygnale [math]X[/math] odzyskujemy tak:

[math]\mathrm{SSVEP} = A S^T[/math]

Modelujemy rejestrowany sygnał jako:

[math]X = \mathrm{SSVEP} + Y [/math]

gdzie:

[math]Y = X-\mathrm{SSVEP}[/math]

to wszystkie komponenty sygnału, które nas nie interesują.

Filtr przestrzenny, który chcemy zbudować powinien maksymalizować stosunek wariancji [math]\mathrm{SSVEP} = A S^T[/math] do wariancji [math]Y = X-\mathrm{SSVEP}[/math]. Macierz kowariancji powinna być uśredniona po powtórzeniach a kowariancja sygnału w każdym powtórzeniu powinna być znormalizowana poprzez podzielenie przez jej ślad (Matlabowa funkcja cov() już wykonuje tę operację). Dalej możemy zastosować technikę znaną z konstrukcji filtrów CSP, tzn. maksymalizacji ilorazu Rayleigh'a za pomocą rozwiązania ogólnionego zagadnienia własnego dla macierzy kowariancji [math]\mathrm{SSVEP} [/math] i [math]Y [/math].

Poniżej prosta demonstracja dla danych zebranych EEG przy stymulacji SSVEP z częstotliwością 38 Hz.

Spakowane dane: Plik:PrzykladoweDaneSSVEP.mat.gz. W oparciu o powyższy opis proszę zaimplementować funkcję cosSinCSP. Prawidłowo zaimplementowana funkcja wraz z poniższym kodem powinna generować rysunek:

% wczytujemy dane
load('PrzykladoweDaneSSVEP.mat');

[numberOfTrials numberOfChannels numberOfSamples] = size(X.data);
namesOfChannels = X.channels;
 
% numberOfChannels numberOfSamples numberOfTrials
W = zeros(numberOfChannels,numberOfChannels);
numberOfHarmonics = 3;
signal = X.data; % (  powtórzenie,  kanał, próbki)
 
S = zeros(size(signal));
W = cosSinCSP(signal,X.stimulation,numberOfHarmonics,X.sampling);
for powt = 1:size(signal,1)
    S(powt,:,:) = W'*squeeze(signal(powt,:,:));
end
 
figure('Name',['Stymulacja: ',num2str(X.stimulation),' Hz'])
for i =1:numberOfChannels
    % rysujemy widma uśrednione po realizacjach dla danych 
    % z oryginalnych kanałów EEG
    subplot(2,8,i)
    PP=0;
    for rep = 1:numberOfTrials
        x = signal(rep,i,:);
        [Pxx,ff] = pwelch(x, X.sampling, 1, X.sampling, X.sampling);
        PP =PP + Pxx;
    end
    plot(ff(ff<60),PP(ff<60))
    title(namesOfChannels{i})
 
    % rysujemy widma uśrednione po realizacjach dla danych 
    % z estymowanych źródeł CSP
    subplot(2,8,8+i)
    PP=0;
    for rep = 1:numberOfTrials
        s = S(rep,i,:);
        [Pss,ff]=pwelch(s, X.sampling, 1, X.sampling, X.sampling);
        PP =PP + Pss;
    end
    plot(ff(ff<60),PP(ff<60))
    title(['źródło CSP: ', num2str(i)])
end

Przykładowy skrypt i dane prezentujący konstrukcję i działanie tego typu filtrów przestrzennych dla pełnych danych z eksperymentu SSVEP: Plik:SSVEP demo csp.tar.gz

ICA jako filtr przestrzenny

Definicja

Independent Component Analysis (ICA) jest metodą statystycznej analizy sygnałów, która dokonuje dekompozycji wielokanałowych zapisów na składowe niezależne w sensie statystycznym. Dwie składowe [math]s_{1}[/math] i [math]s_{2}[/math] są niezależne jeżeli wiedza o wartości [math]s_{1}[/math] nie daje żadnych informacji o możliwych wartościach [math]s_{2}[/math]. ICA może być wyrażona przez prosty model generatywny:

[math] \mathbf{x} = \mathbf{D}\mathbf{s} [/math]

gdzie [math]\mathbf{x}=\{x^{1},x^{2},\dots, x^{n}\}[/math] jest zmierzonym [math]n[/math] kanałowym sygnałem, [math]\mathbf{D}[/math] jest macierzą mieszającą zaś [math]\mathbf{s}=\{s^{1},s^{2},\dots,s^{n} \}[/math] jest aktywnością [math]n[/math] źródeł. Podstawowym założeniem dotyczącym [math]\mathbf{s}[/math] jest to, że [math]s^{i}[/math] są statystycznie niezależne. Aby wyestymować model musimy też założyć, że składowe mają niegaussowskie rozkłady wartości (Hyvarinen, 2000).

Dodatkowo model ten zakłada następujące fakty:

1. Sygnał jest liniową mieszaniną aktywności źródeł
2. Sygnały pochodzące z każdego ze źródeł są niezależne od pozostałych
3. Źródła oraz proces ich mieszania są stacjonarne, tzn, ich momenty statystyczne nie zależą od czasu
4. Energie (wariancje) źródeł nie mogą być wyznaczone jednoznacznie. Dzieje się tak ponieważ pomnożenie amplitudy [math]i-{tego}[/math] źródła może być uzyskane poprzez przemnożenie albo [math]s^{i}[/math] albo przez przemnożenie [math]i-tej[/math] kolumny macierzy [math]\mathbf{D}[/math]}. Naturalnym rozwiązaniem tej niejednoznaczności jest wprowadzenie konwencji, że komponenty są normowane tak aby miały wariancję 1: [math]E[s^{i}]=1[/math].
5. Kolejność komponentów jest dowolna. Bo jeśli: w ten sam sposób zmienimy kolejność komponentów w [math]\mathbf{s}[/math], i kolumn w [math]\mathbf{D}[/math] to dostaniemy dokładnie ten sam sygnał [math]\mathbf{x}[/math].

Głównym wyzwaniem w analizie ICA jest estymacja macierzy mieszającej [math]\mathbf{D}[/math]. Gdy jest ona znana to komponenty mogą być wyliczone w następujący sposób:

[math] \mathbf{s} = \mathbf{D}^{-1}\mathbf{x} [/math]

Estymacja

Znalezienie niezależnych komponentów może być rozważane w świetle Centralnego Twierdzenia Granicznego jako poszukiwanie komponentów o możliwie nie gaussowskim rozkładzie. Aby zrozumieć to podejście prześledźmy heurystykę zaproponowaną przez (Hyvarinen, 2000). Dla prostoty załóżmy, że poszukiwane źródła niezależne mają identyczne rozkłady. Zdefiniujmy [math]y = \mathbf{w}^{\mathsf{T}}\mathbf{x}[/math]. Zauważmy, że jeśli [math]\mathbf{w}^{\mathsf{T}}[/math] jest jedną z kolumn macierzy [math]\mathbf{D}^{-1}[/math], to [math]y[/math] jest jednym z poszukiwanych komponentów. Zamieniając zmienne [math]\mathbf{z}=\mathbf{D}^{\mathsf{T}}\mathbf{w}[/math] możemy napisać [math]y = \mathbf{w}^{\mathsf{T}}\mathbf{x} = \mathbf{w}^{\mathsf{T}} \mathbf{D}\mathbf{s} = \mathbf{z}^{\mathsf{T}}\mathbf{s}[/math]. To uwidacznia fakt, że [math]y[/math] jest liniową kombinacją składowych [math]s^{i}[/math] z wagami danymi przez [math]z_{i}[/math]. Z centralnego twierdzenia granicznego wynika, że suma niezależnych zmiennych losowych ma bardziej gaussowski charakter niż każda z tych zmiennych osobno. Liniowa kombinacja staje się najmniej gaussowska gdy [math]\mathbf{z}[/math] ma tylko jeden element niezerowy. W tym przypadku [math]y[/math] jest proporcjonalny do [math]s^{i}[/math]. Zatem problem estymacji modelu ICAmoże być sformułowany jako problem znalezienia takiego [math]\mathbf{w}[/math] , który maksymalizuje niegaussowskość [math]y=\mathbf{w}^{\mathsf{T}}\mathbf{x}[/math]. Maksymalizacja niegaussowskości [math]y[/math] daje jeden niezależny komponent odpowiadający jednemu z [math]2n[/math] maksimów (bo mamy [math]s^{i}[/math] i [math]-s^{i}[/math]) w krajobrazie optymalizacyjnym. Aby znaleźć wszystkie niezależne komponenty musimy znaleźć wszystkie maksima. Ponieważ komponenty są nieskorelowane, to poszukiwania kolejnych komponentów można kontynuować w podprzestrzeni ortogonalnej do już znalezionych komponentów.

Obliczenia

Intuicyjna heurystyka poszukiwania najbardziej niegaussowskich składowych może być użyta do wyprowadzenia różnych funkcji kosztu, których optymalizacja daje model ICA, np. kurtoza. Procedura wykorzystywana w eeglabie (“runica”, Makeig 1996) dąży do minimalizacji informacji wzajemnej. Oba podejścia są w przybliżeniu równoważne (Hyvarinen, 2000), chociaż owo przybliżenie dla sygnałów elektrofizjologicznych nie zostało to jeszcze w pełni wyeksplorowane. Dla sygnałów o niskiej wymiarowości i spełniających dokładnie założenia ICA wszystkie powszechnie wykorzystywane algorytmy dają niemal identyczne wyniki.

Bardzo ważna uwaga

ogólną zasadą jest, że jeśli estymujemy [math]N[/math] stabilnych komponentów (z [math]N[/math]-kanałowych danych) to musimy dysponować [math]k N^2[/math] punktami danych w każdym kanale, gdzie [math]N^2[/math]jest liczbą elementów w macierzy [math]\mathbf{D}[/math], którą ICA próbuje wyestymować, [math]k[/math] jest liczbą całkowitą. Nie ma dobrych oszacowań teoretycznych na wielkość [math]k[/math], z praktycznych obserwacji wynika, że rośnie on z ilością kanałów.

Możliwe zastosowania

Najczęściej ICA jest stosowana jako narzędzie do:

• usuwania artefaktów z sygnałów EEG (ruchy oczu i mięśnie)
• wydobywania składowych do dalszej analizy (Onton, 2006)
• jako analiza wstępna do lokalizacji źródeł (Grau, 2007).
• ICA jest także stosowana w analize sygnałów EKG i EMG.

Bibliografia

• Grau, C., Fuentemilla, L., Marco-Pallars, J. (2007). Functional neural dynamics underlying auditory event-related n1 and n1 suppression response. Neuroimage, 36(6):522–31.
• Hyvarinen, A. and Oja, E. (2000). Independent component analysis: Algorithms and applications. Neural Networks, 13(4-5):411–430.
• Makeig,S.,Bell,A.,Jung,T.-P., Sejnowski,T.(1996).Independentcomponent analysis of electroencephalographic data. W: Touretzky, D., Mozer, M., and Hasselmo, M., editors, Advances in Neural Information Processing Systems, volume 8, pages 145–151. MIT Press, Cambridge, MA.
• Onton,J., Makeig,S.(2006).Information-based modeling of event-related brain dynamics. Prog Brain Res., 159:99–120.
• Tutorial: http://sccn.ucsd.edu/wiki/Chapter_09:_Decomposing_Data_Using_ICA
• http://sccn.ucsd.edu/~arno/indexica.html
• http://cis.legacy.ics.tkk.fi/aapo/papers/IJCNN99_tutorialweb/

Wydobywanie interesujących komponentów

Dane do tej części ćwiczeń proszę pobrać i rozpakować w swoim katalogu: http://www.fuw.edu.pl/~jarekz/LabEEG/Dane_do_ICA_alfa.tar.gz

Pochodzą one z eksperymentu, w którym osoba badana siedziała z zamkniętymi oczami słuchając nagrania czytanego spokojnym głosem. Metadane opisujące sygnał znajdują się w pliku Miro.xml, zaś lokalizacje elektrod w pliku Miro-10-20-Cap.locs.

Proszę:

• wczytać dane do eeglaba
• wyedytować lokalizację elektrod
• usunąć kanały nie zawierające EEG
• zmienić referencje na średnią z kanałów A1 i A2
• przefiltrować filtrem FIR górnoprzepustowym z częstością odcięcia 0,5 Hz
• obejrzeć wstępnie przygotowane dane
• policzyć ICA na całym sygnale
• obejrzeć właściwości otrzymanych komponentów
  • Czy są wśród nich takie, które zawierają znaczny udział rytmu alfa?
  • Jaka jest ich topografia?
• usunąć wszystkie komponenty nie zawierające alfy
• odtworzyć z tych komponentów sygnał na elektrodach
• wykoać dekompozycję ICA kilkukrotnie (co najmniej 3) i porównać wyniki
  • Czy uzyskiwane komponenty są powtarzalne?
  • Swoje wyniki porównać też z sąsiednimi grupami.

Identyfikacja artefaktów

Proszę pobrać dane:

• http://www.fuw.edu.pl/~jarekz/LabEEG/Arousal-10-20-Cap.locs
• http://www.fuw.edu.pl/~jarekz/LabEEG/Arousal1.set
• http://www.fuw.edu.pl/~jarekz/LabEEG/Arousal1.fdt

Pochodzą one z eksprymentu w którym osoba badana czytała słowa o różych właściwościach wzbudznia emocji.

• wczytaj je do eeglab'a
• wczytaj lokalizację kanałów z pliku Arousal-10-20-Cap.locs
• obejrzyj przebiegi czasowe
• odrzuć kanał z diodą (21) i z GSR (20)
• zrób dekompozycję ICA
• obejrzyj topografię komponentów.
• zidentyfikuj komponenty odpowiadające mruganiu i aktywności mięśniowej