Matematyka 1 OO/Niestandardowe metryki: Różnice pomiędzy wersjami
| Linia 346: | Linia 346: | ||
w początku układu współrzędnych. | w początku układu współrzędnych. | ||
| − | [[File:MatematykaOptykaOkularowa_cwicz_sem1_picture_11. | + | [[File:MatematykaOptykaOkularowa_cwicz_sem1_picture_11.png]] |
Okrąg w metryce “rzymskiej” o środku w punkcie | Okrąg w metryce “rzymskiej” o środku w punkcie | ||
Aktualna wersja na dzień 17:40, 26 maj 2015
Zadanie
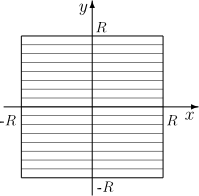
Znaleźć koło o promieniu [math]R[/math] i środku w początku układu współrzędnych w metryce “miejskiej” zadanej wzorem
- [math] {\rm d}(A,B)=|x_B-x_A|+|y_B-y_A| [/math]
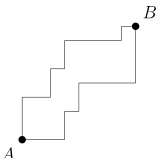
Warto wyjaśnić, skąd bierze się nazwa “metryka miejska”. Odległość między dwoma punktami [math]A[/math] i [math]B[/math] nie jest zwykłą długością odcinka łączącego te punkty, tylko długością krzywej łamanej złożonej z odcinków równoległych do jednej z osi układu współrzędnych. To odpowiada drodze, jaką musimy przebyć, jeśli możemy się poruszać tylko ulicami, z których każda ma kierunek wschód-zachód lub północ-południe.
Suma długości odcinków poziomych jest równa różnicy współrzędnych [math]X[/math] obu punktów, a suma długości odcinków pionowych jest równa różnicy współrzędnych [math]y[/math].
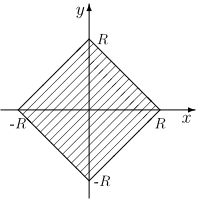
Szukane koło składa się z punktów [math]A[/math] spełniających warunek
- [math] {\rm d}(A,O)=|x_A|+|y_A|\le R [/math]
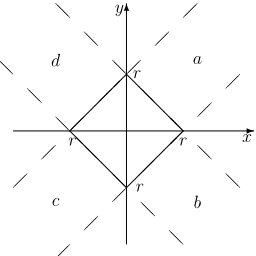
Zacznijmy od okręgu o promieniu [math]r[/math]:
- [math] |x_A|+|y_A|=r [/math]
Najłatwiej jest rozwiązać to równanie po kolej w każdej ćwiartce układu współrzędnych
| a) | [math]x\gt 0,\,\,y\gt 0[/math]: | [math]x+y=r[/math] | [math]\Rightarrow [/math] | [math]y=-x+r[/math] |
| b) | [math]x\gt 0,\,\,y\lt 0[/math]: | [math]x-y=r[/math] | [math]\Rightarrow [/math] | [math]y=x-r[/math] |
| c) | [math]x\lt 0,\,\,y\lt 0[/math]: | [math]-x-y=r[/math] | [math]\Rightarrow [/math] | [math]y=-x-r[/math] |
| d) | [math]x\lt 0,\,\,y\gt 0[/math]: | [math]-x+y=r[/math] | [math]\Rightarrow [/math] | [math]y=x+r[/math] |
Rysujemy wykresy wszystkich czterech linii prostych zadanych równaniami [math]y=\mp x \mp r[/math] i na każdej z nich zaznaczmy odcinek spełniający odpowiedni warunek na znaki [math]x[/math] i [math]y[/math]
Koło o promieniu [math]R[/math] jest sumą okręgów o promieniach [math]r\le R[/math]
Zadanie
Znaleźć koło o promieniu [math]R[/math] i środku w początku układu współrzędnych w metryce “max” zadanej wzorem
- [math] {\rm d}(A,B)=\max \left\lbrace |x_B-x_A|,|y_B-y_A|\right\rbrace [/math]
Takie koło składa się z punktów [math]A[/math] spełniających warunek
- [math] {\rm d}(A,O)=\max \left\lbrace |x_A|,|y_A|\right\rbrace \le R [/math]
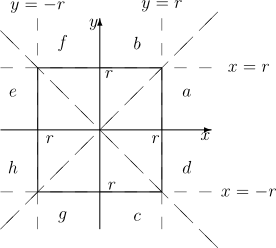
Zacznijmy od okręgu o promieniu [math]r[/math]:
- [math] \max \left\lbrace |x_A|,|y_A|\right\rbrace =r [/math]
To równanie rozwiązujemy po kolej w każdej ćwiartce układu współrzędnych. Dodatkowa komplikacja polega na tym, że każdą ćwiartkę musimy podzielić na dwa obszary: [math]|x|\gt |y|[/math] i [math]|x|\lt |y|[/math].
| a) | [math]x\gt y\gt 0[/math]: | [math]\max \lbrace |x|,|y|\rbrace =|x|=x[/math] | [math]\Rightarrow [/math] | [math]x=r[/math] |
| b) | [math]y\gt x\gt 0[/math]: | [math]\max \lbrace |x|,|y|\rbrace =|y|=y[/math] | [math]\Rightarrow [/math] | [math]y=r[/math] |
| c) | [math]|y|\gt x\gt 0\gt y[/math]: | [math]\max \lbrace |x|,|y|\rbrace =|y|=-y[/math] | [math]\Rightarrow [/math] | [math]y=-r[/math] |
| d) | [math]x\gt 0\gt y\gt -|x|[/math]: | [math]\max \lbrace |x|,|y|\rbrace =|x|=x[/math] | [math]\Rightarrow [/math] | [math]x=r[/math] |
| e) | [math]|x|\gt y\gt 0\gt x[/math]: | [math]\max \lbrace |x|,|y|\rbrace =|x|=-x[/math] | [math]\Rightarrow [/math] | [math]x=-r[/math] |
| f) | [math]0\gt x\gt y[/math]: | [math]\max \lbrace |x|,|y|\rbrace =|y|=-y[/math] | [math]\Rightarrow [/math] | [math]y=-r[/math] |
| g) | [math]0\gt x\gt y[/math]: | [math]\max \lbrace |x|,|y|\rbrace =|y|=-y[/math] | [math]\Rightarrow [/math] | [math]y=-r[/math] |
Koło o promieniu [math]R[/math] jest sumą okręgów o promieniach [math]r\le R[/math]
Zadanie
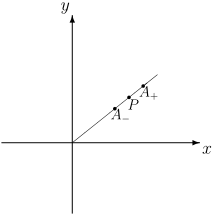
Znaleźć koło o promieniu [math]R[/math] i środku w ustalonym punkcie [math]P=(x_P,y_P)[/math] w metryce “rzymskiej” zadanej wzorem
- [math] {\rm d}(A,B)=\left\lbrace \begin{array}{ll} \sqrt{(x_B-x_A)^2+(y_B-y_A)^2} & \exists _c\,\, [x_B,y_B]=c[x_A,y_A] \\[6pt] \sqrt{x_A^2+y_A^2}+\sqrt{x_B^2+y_B^2} & w innych przypadkach \end{array} \right. [/math]
Warunek w pierwszej linii powyższego wzoru opisuje przypadek, gdy punkty [math]A[/math] i [math]B[/math] leżą na jednej prostej przechodzącej przez początek układu współrzędnych (“Rzym”). Dla takich punktów ich wzajemna odległość jest równa zwykłej odległości euklidesowej [math]\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}[/math]. W innych przypadkach (dolna linia powyższego wzoru) odległość punktów [math]A[/math] i [math]B[/math] jest sumą odległości każdego z tych punktów od początku układu współrzędnych. (Jeśli dwa punkty leżą na różnych “drogach prowadzących do Rzymu”, to aby się dostać z jednego z nich do drugiego musimy przejechać przez “Rzym”).
Szukane koło składa się z punktów [math]A[/math] spełniających warunek
- [math] {\rm d}(A,P)\le R [/math]
Jak zwykle, zacznijmy od okręgu o promieniu [math]r[/math]. W tym przypadku musimy być jednak bardziej uważni, niż w zadaniach poprzednich. Powodem jest to, że w metryce “rzymskiej” kształt koła zależy od jego promienia. Dla małych [math]r[/math], kołem (o środku różnym od początku układu współrzędnych) są dwa punkty leżące na półprostej łączącej dany punkt z początkiem układu współrzędnych, odległe od [math]P[/math] o [math]r[/math]:
- [math] r=\sqrt{(x_A-x_P)^2+(y_A-y_P)^2} \qquad \qquad [x_A,y_A]=c[x_P,y_P] [/math]
Podstawiając drugie z tych równań do pierwszego, podniesionego stronami do kwadratu, dostajemy
- [math] r^2 = (cx_P-x_P)^2+(cy_P-y_P)^2 = (c-1)^2(x_P^2+y_P^2) [/math]
Obliczamy stąd liczbę [math]c[/math]:
- [math] (c-1)^2=\frac{r^2}{x_P^2+y_P^2} [/math]
- [math] c-1=\pm \frac{r}{\sqrt{x_P^2+y_P^2}} [/math]
- [math] c=1\pm \frac{r}{\sqrt{x_P^2+y_P^2}} [/math]
Wstawiając [math]c[/math] do warunku łączącego współrzędne punktu [math]A[/math] ze współrzędnymi punktu [math]P[/math] (warunek opisujący fakt, że [math]A[/math] i [math]P[/math] leżą na jednej półprostej zaczynającej się w środku układu współrzędnych)
- [math] [x_A,y_A]=c[x_P,y_P] [/math]
otrzymujemy
[math]\begin{matrix} x_{A_\pm }=x_P\pm \frac{rx_P}{\sqrt{x_P^2+y_P^2}} \\ y_{A_\pm }=y_P\pm \frac{ry_P}{\sqrt{x_P^2+y_P^2}} \end{matrix}[/math]
Kształt koła o promieniu [math]r[/math] jest inny dla [math]r\gt \sqrt{x_P^2+y_P^2}[/math]. Punkty [math]A_-[/math] i [math]A_+[/math] nadal leżą na prostej [math]OP[/math], z tym, że [math]A_-[/math] znajduje się “po drugiej stronie” początku układu współrzędnych, co odpowiada ujemnej wartości współczynnika [math]c[/math]:
- [math] c_-=1-\frac{r}{\sqrt{x_P^2+y_P^2}}\lt 0 [/math]
Okrąg o promieniu [math]r\gt \sqrt{x_P^2+y_P^2}[/math] zawiera jednak nie tylko punkty [math]A_-[/math] i [math]A_+[/math], ale także punkty niewspółliniowe z [math]O[/math] i [math]P[/math]. Położenie takich punktów znajdujemy korzystając ze wzoru na odległość punktów nie leżących na jednej “drodze” prowadzącej do “Rzymu”:
- [math] d(A,P)=\sqrt{x_A^2+y_A^2}+\sqrt{x_P^2+y_P^2} [/math]
Przyrównujemy te odległość do [math]r[/math]:
- [math] r=\sqrt{x_A^2+y_A^2}+\sqrt{x_P^2+y_P^2} [/math]
- [math] x_A^2+y_A^2=\left(r-\sqrt{x_P^2+y_P^2}\right)^2 [/math]
Jest to zwykły okrąg o promieniu [math]r-\sqrt{x_P^2+y_P^2}[/math] i środku w początku układu współrzędnych.
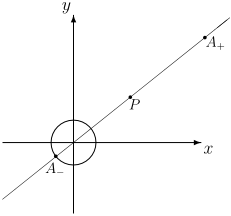
Okrąg w metryce “rzymskiej” o środku w punkcie [math]P=(x_P,y_P)[/math] i promieniu [math]r\gt \sqrt{x_P^2+y_P^2}[/math] jest sumą zwykłego okręgu o środku w początku układu współrzędnych i promieniu [math]r-\sqrt{x_P^2+y_P^2}[/math] i punktu [math]A_+[/math] leżącego na półprostej [math]OP[/math] w odległości [math]r[/math] od punktu [math]P[/math].
Znając kształty okręgów, możemy wyznaczyć postać kół o środku w punkcie [math]P=(x_P,y_P)[/math]. Jeśli promień koła [math]R[/math] jest nie większy niż [math]\sqrt{x_P^2+y_P^2}[/math], to kołem o tym promieniu jest suma “dwupunktowych” okręgów o [math]r\le R[/math], czyli
Jeśli promień [math]R[/math] przekracza wartość [math]\sqrt{x_P^2+y_P^2}[/math], koło jest sumą odcinka i zwykłego koła o środku w początku układu współrzędnych i promieniu [math]R-\sqrt{x_P^2+y_P^2}[/math]
Na koniec pozostaje rozpatrzeć przypadek, gdy środek okręgu [math]P[/math] pokrywa się z początkiem układu współrzędnych [math]O[/math]. W takim przypadku odległość w metryce “rzymskiej” sprowadza się do odległości euklidesowej
- [math] d(A,O)=\sqrt{x_A^2+y_A^2} [/math]
i koło o promieniu [math]R[/math] jest zwykłym kołem o takim samym promieniu i środku w początku układu współrzędnych.
Zadanie
Warto zrobić proste zadanie, które pokazuje, że mówienie o różnych metrykach nie jest tylko “akademicką zabawą”. Można np. zadać pytanie: jaka jest odległość z Gdyni do Kapsztadu. Przyjmujemy następujące dane: oba miasta mają taką samą długość geograficzną (około [math]18^{\circ }30^{\prime }[/math]E), a szerokości geograficzne odpowiednio [math]54^{\circ }30^{\prime }[/math]N i [math]34^{\circ }[/math]S, natomiast promień Ziemi wynosi [math]R=6370[/math] km.
Odpowiedzi na pytanie od odległość między tymi dwoma miastami mogą być aż trzy:
-
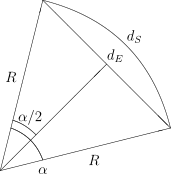
Oba miasta leżą na jednym południku, który jest (w przybliżeniu)
okręgiem o promieniu [math]R[/math]. Kąt między promieniami tego okręgu
przechodzącymi przez te miasta wynosi
[math]\alpha =54,5^\circ +34^\circ =88,5^\circ [/math].
Odległość w trójwymiarowej przestrzeni euklidesowej wynosi więc
- [math] d_E=2R\sin \left(\frac{\alpha }{2}\right) [/math]
-
Odległość mierzona wzdłuż okręgu, czyli po powierzchni Ziemi
wynosi
- [math] d_S=R\alpha ,\, [/math]
- [math] \alpha =\pi \frac{88,5}{180} [/math]
- [math] \sin \left(\frac{\alpha }{2}\right)\lt \frac{\alpha }{2} \qquad \Rightarrow \qquad d_E\lt d_S [/math]
- Odległość między dwoma portami można też zdefiniować, jako długość drogi, jaką musi przebyć statek. Jest ona większa od obu poprzednich odległości i na dodatek dość skomplikowana (zależy od kształtu i położenia kontynentów).
Odległości a) i b) można opisać dwiema metrykami na okręgu (wydaje się, że wprowadzanie metryki na sferze może być zbyt skomplikowane dla słuchaczy tych zajęć):
- [math] d_E(\phi _1,\phi _2)=2R\sin \left(\frac{\phi _2-\phi _1}{2}\right),\, [/math]
- [math] d_S(\phi _1,\phi _2)=R|\phi _1-\phi _2|,\, [/math]
gdzie [math]\phi _i[/math] są wartościami wspołrzędnej kątowej opisującej położenie danych punktów na okręgu.