TI/Programowanie dla Fizyków Medycznych/RRZ: Różnice pomiędzy wersjami
| Linia 265: | Linia 265: | ||
Omegas=np.arange(0.1,3.0,0.05) | Omegas=np.arange(0.1,3.0,0.05) | ||
</source> | </source> | ||
| − | Możemy teraz dla każdej z wartości W rozwiązać numerycznie równanie | + | Możemy teraz dla każdej z wartości W rozwiązać numerycznie równanie różniczkowe i wyznaczyć odpowiadającą amplitudę oscylacji |
| − | + | <source lang="python"> | |
| − | + | amp=[amplituda(RK4(oscylator,[0.0,1.0],0.0,400.0,0.1)[1]) for oscylator.W in Omegas] | |
| − | + | </source> | |
| − | + | Wynik koncowy wyglada następująco | |
| − | + | <source lang="python"> | |
| − | + | py.plot(Omegas,amp) | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
py.show() | py.show() | ||
</source> | </source> | ||
| + | [[Plik:Przykład.jpg]] | ||
| + | Jak można było się domyślić amplituda jest największa gdy częstotliwość wymuszania W pokrywa się z wartością częstotliwości drgań własnych <math> w_0=1 </math> | ||
| − | + | ===Zadanie - Układ Lorenza=== | |
| − | ===Zadanie=== | ||
Rozwiąż układ równań różniczkowych Lorenza dany wzorami | Rozwiąż układ równań różniczkowych Lorenza dany wzorami | ||
| Linia 292: | Linia 285: | ||
metodą całkowania Rungego–Kutty drugiego rzędu z α = 2/3, czyli | metodą całkowania Rungego–Kutty drugiego rzędu z α = 2/3, czyli | ||
| − | <math> k_1 &= f(t_n, | + | <math>k_1 &= f(t_n,x_n)</math> , |
| + | |||
| + | <math>k_2 &= f(t_n + \tfrac{2}{3}h, x_n + \tfrac{2}{3}h k_1)</math> , | ||
| + | |||
| + | <math>x_{n+1} &= x_n + h \left(\tfrac{1}{4}k_1+\tfrac{3}{4} k_2 \right). </math> | ||
Przyjmij sigma=10, b=8/3, r=99.96, krok czasowy h=0.005 i warunki początkowe x=1,y=0,z=0. Wykonaj 8000 kroków czasowych. Układ po pewnym czasie zacznie poruszać się po pewnej periodycznej trajektorii. Wykonaj 3 rysunki TEJ PERIODYCZNEJ TRAJEKTORII (bez okresu dochodzenia do niej) w płaszczyznach (x,y), (y,z) i (z,x). Wypisz na ekranie przedziały wartości jakie przyjmują zmienne x,y i z na periodycznej trajektorii oraz okres trajektorii periodycznej. | Przyjmij sigma=10, b=8/3, r=99.96, krok czasowy h=0.005 i warunki początkowe x=1,y=0,z=0. Wykonaj 8000 kroków czasowych. Układ po pewnym czasie zacznie poruszać się po pewnej periodycznej trajektorii. Wykonaj 3 rysunki TEJ PERIODYCZNEJ TRAJEKTORII (bez okresu dochodzenia do niej) w płaszczyznach (x,y), (y,z) i (z,x). Wypisz na ekranie przedziały wartości jakie przyjmują zmienne x,y i z na periodycznej trajektorii oraz okres trajektorii periodycznej. | ||
Wersja z 13:23, 6 cze 2015
Spis treści
Równania różniczkowe zwyczajne
Zajmieny się teraz problemem numerycznego rozwiązywania równań różniczkowych zwyczajnych o postaci:
[math] \frac{dy(t)}{dt} = f(t,y(t))[/math],
z warunkeim początkowym
[math]y(t_0)=y_0[/math].
Zauważmy, że przykładowe równanie różniczkowe drugiego rzędu
[math] \frac{d^2 x(t)}{dt^2} = \omega(t,x(t))[/math],
można zapisać jako
[math] \frac{d}{dt} \binom{x(t)}{x'(t)} = \binom{x'(t)}{\omega(t,x(t))}[/math].
W analogiczny sposób równanie dowolnego rzędy możemy zapisać jako wektorowe równanie różniczkowe pierwszego rzędu. Wystarczy zatem, że skupimy się na rozwiązywaniu równań pierwszego rzędu, Rozwiązaniem postawionego problemu są ciągłe funkcje zmiennej czasowej t. Rozwiązanie numeryczne takiego problemu ogranicza się jednak do znalezienia wartości funkcji y(t) w skończonej liczbie punktów czasowych. W najprostrzym przypadku (do którego się tutaj ograniczymy) zakładamy, że punkty te są od siebie równo oddalone, a odległość między nimi nazywamy krokiem czasowym i tradycyjnie oznaczamy literą h. Zatem rozwiązanie równania na przedziale [math](t_0,t_k)[/math] sprwadzamy do rozwiązania w sekwencji czasów [math]t_0, t+1=t_0+h,t_2=t_0+2h,...,t_k=Nh[/math]. Poprzez [math]x_n[/math] oznaczać będziemy numeryczne przybliżenie ścisłego rozwiązania [math]x(t_n)[/math].
Metoda Eulera
Najprostszą metodą numeryczną rozwiązywania równań różniczkowych jest metoda Eulera. Przybliżmy pochodzną czasową występującą po lewej stronie równania przez iloraz różnicowy
[math] \frac{d x(t)}{dt} \approx \frac{x(t+h)-x(t)}{h}[/math],
przekształacjąc uzyskujemy
[math] x(t+h) \approx x(t)+ h \frac{d x(t)}{dt} [/math]
a po podstawieniu rozwiązywanego równania mamy
[math] x(t+h) \approx x(t)+ h f(t,x(t)) [/math].
Możemy to zapisać w postaci dyskretnej
[math] x_{n+1} = x_n + h f(t_n,x_n) [/math].
Wartość w kolejnej chwili czasu dana jest explicite poprzez wartość w chwili poprzedniej. Metoda ta nazywa się Explicit Euler. Możemy teraz zaimplementować ją w pythonie
import numpy as np
import pylab as py
#rozwiazujemy rownanie dx(t)/dt=f(t,x)
#metoda Explicit Euler
#f - funkcja f z rownania
#x0-wartosc poczatkowa
#t0-czas poczatkowy
#tk-czas koncowy
#h-krok czasowy
def EE(f,x0,t0,tk,h):
#generujemy wektor czasow
t=np.arange(t0,tk,h)
#liczba krokow czasowych
N=len(t)
#wektor wynikowy
if hasattr(x0, "__len__"): x=np.zeros((N,len(x0))) # gdy mamy doczynienia w równaniem wektorowym
else: x=np.zeros(N) #dla przypadku skalarnego
#wpisujemy wartosc poczatkowa
x[0]=np.array(x0)
#index
i=1
#petla glowna
while (i<N):
x[i]=np.array(x[i-1]+h*f(t[i-1],x[i-1]))
i+=1
return t,x
Najłatwiej będzie przetestować napisaną metodę na równaniu którego ścisłe rozwiązanie jest znane.Zacznijmy zatem od równania oscylatora harmonicznego
def oscylator(t,y):
x=y[0]
xdot=y[1]
return np.array([xdot,-x])
Rozwiążmy to równanie z warunkeim początkowym [1.0,1.0] i od czasu od 0 do 100.
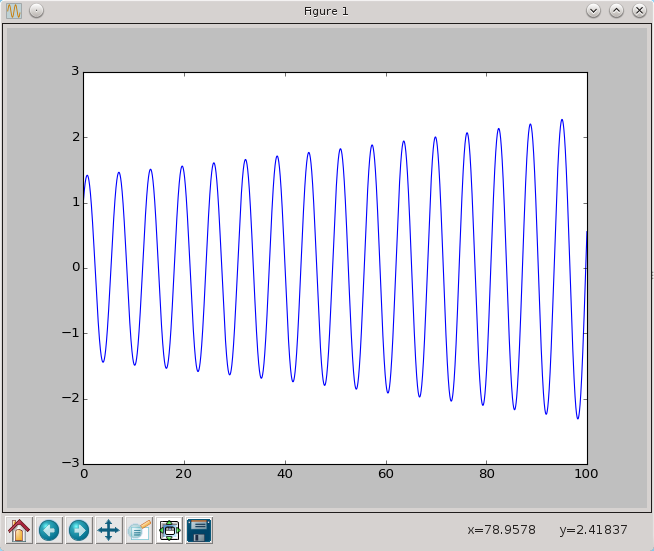
t,x=EE(oscylator,[1.0,1.0],0.0,100,0.01)
py.plot(t,x[:,0])
py.show()
rozwiązanie wygląda wówczas nastepująco
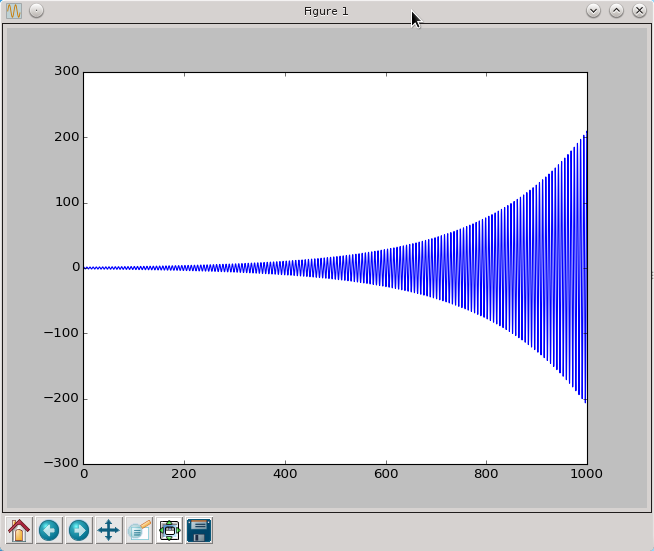
Jeżeli zaś wydłuzymy czas symulacji to 1000 otrzymamy
Amplituta oscylacji rośnie wykładniczo i rozwiązanie numeryczne bardzo szybko przestaje mieć cokolwiek wspólnego ze ścisłym rozwiązaniem którego amplituda jest przecież stała. Metoda Explicit Euler już po kilku krokach czasowych przestaje przypominać ścisłe rozwiązanie. Niestety trudno jest zupełnie wyeliminować to zjawisko, za to możemy użyć metody, która znacznie wolniej będzie się oddalać od ścisłego rozwiązania. Zauważmy, że w metodzie Explicit Euler w każdym kroku czasowym tylko raz liczyliśmy wartość funkcji f. Liczbę wywołan funkcji f w każdym kroku czasowym nazywamy rzędem metody, stąd Explicit Euler jest metodą pierwszego rzędu. Wprowadźmy teraz przykładowe metody rzędu drugiego
Metoda Żabiego Skoku
W poprzedniej metodzie liczyliśmy wartość funkcji f w chwili [math]t_n[/math], która była pochodzną po czasie naszego ścisłego rozwiązania. Kolejny punkt [math]x_{n+1}[/math] był liczony z przybliżenia liniowego funkcji w chwili poprzedniej. Jeżeli faktyczna trajektoria ma niezerową drugą pochodzną to takie liniowe przybliżenie zawsze będzie nas oddalało od ścisłego rozwiązania. Dosyć prostym pomysłem na poprawienie zbieżności metody jest tak zwany żabi skok. Policzmy najpierw wartość zmiennej x przesuwając się w czasie o h/2 i policzmy wówczas pochodną, którą oznaczmy przez [math]k_2[/math]
[math] k_1=f(t_n,x_n) [/math].
[math] k_2=f(t_n+h/2,x_n+h/2*k_1) [/math].
Nastepnie używamy pochodznej [math] k_2 [/math] zamiast pochodznej [math] k_1 [/math] do obliczenia wartości funkcji w kolejnym kroku czasowym.
[math] x_{n+1} = x_n + h k_2 [/math].
Przykładowa implementacja tej metody wygląda nastepująco
def leapfrog(f,x0,t0,tk,h):
#generujemy wektor czasow
t=np.arange(t0,tk,h)
#liczba krokow czasowych
N=len(t)
#wektor wynikowy
if hasattr(x0, "__len__"): x=np.zeros((N,len(x0)))
else: x=np.zeros(N)
#wpisujemy wartosc poczatkowa
x[0]=np.array(x0)
#index
i=1
#petla glowna
while (i<N):
k1=f(t[i-1],x[i-1])
k2=f(t[i-1]+h*0.5,x[i-1]+0.5*h*k1)
x[i]=np.array(x[i-1]+h*k2)
i+=1
return t,x
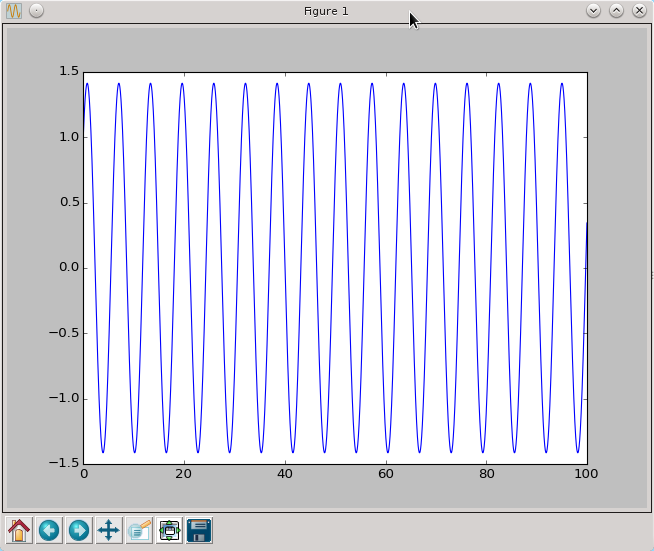
Rozwiązanie równania oscylatora tą metodą dla identycznych jak poprzednio czasów da nastepujące wyniki
t,x=leapfrog(oscylator,[1.0,1.0],0.0,100,0.01)
py.plot(t,x[:,0])
py.show()
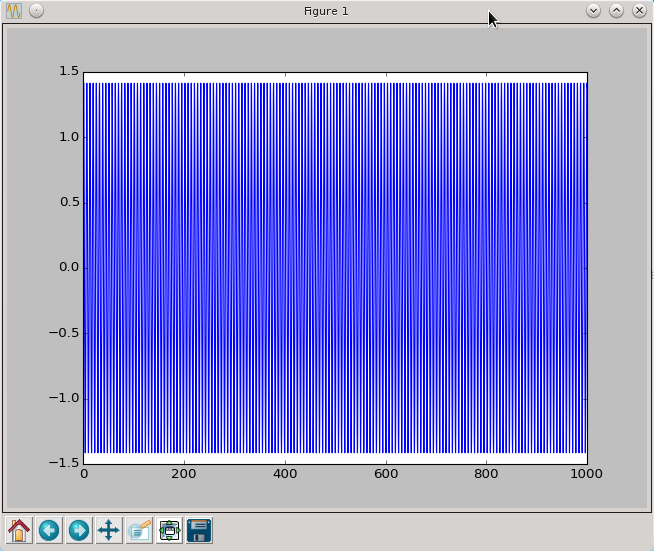
t,x=leapfrog(oscylator,[1.0,1.0],0.0,1000,0.01)
py.plot(t,x[:,0])
py.show()
Metoda Heuna
Kolejną metodą niewiele różniącą się od poprzedniej jest metoda Heuna. Zdefiniowana jest ona przez równania [math] k_1=f(t_n,x_n) [/math],
[math] k_2=f(t_n+h/2,x_n+h/2*k_1) [/math],
[math] x_{n+1} = x_n + h k_2 [/math].
Implementacja wygląda następująco
def Heun(f,x0,t0,tk,h):
#generujemy wektor czasow
t=np.arange(t0,tk,h)
#liczba krokow czasowych
N=len(t)
#wektor wynikowy
if hasattr(x0, "__len__"): x=np.zeros((N,len(x0)))
else: x=np.zeros(N)
#wpisujemy wartosc poczatkowa
x[0]=np.array(x0)
#index
i=1
#petla glowna
while (i<N):
k1=f(t[i-1],x[i-1])
k2=f(t[i-1]+h*0.5,x[i-1]+0.5*h*k1)
x[i]=np.array(x[i-1]+h*0.5*(k1+k2))
i+=1
return t,x
Runge-Kutta czwartego rzędu
Ostatnią metodą, którą omówimy jest najbardziej popularna metoda zwana w skrócie RK4. Metoda to uznawana jest za kanoniczną i w większości zastosowań dającą najlepsze wyniki. Metody wyższego rzędu nie wnoszą już do wyniku znaczącej poprawy. Jak sugeruje nazwa metody, jej rząd to 4, czyli w każdym kroku czasowym czterokrotnie wywołujemy funkcję f. Metoda ta zdefiniowana jest wzorami
[math] k_1 = f \left( t_n, x_n \right) [/math],
[math] k_2 = f \left( t_n + {h \over 2}, x_n + {1 \over 2} k_1 \right) [/math],
[math] k_3 = f \left( t_n + {h \over 2}, x_n + {1 \over 2} k_2 \right) [/math],
[math] k_4 = f \left( t_n + h, x_n + k_3 \right) [/math],
[math] x_{n+1} = x_n + {h \over 6} (k_1 + 2k_2 + 2k_3 + k_4) [/math],
a implementacja wygląda następująco
def RK4(f,x0,t0,tk,h):
#generujemy wektor czasow
t=np.arange(t0,tk,h)
#liczba krokow czasowych
N=len(t)
#wektor wynikowy
if hasattr(x0, "__len__"): x=np.zeros((N,len(x0)))
else: x=np.zeros(N)
#wpisujemy wartosc poczatkowa
x[0]=np.array(x0)
#index
i=1
#petla glowna
while (i<N):
k1=h*f(t[i-1],x[i-1])
k2=h*f(t[i-1]+h*0.5,x[i-1]+0.5*k1)
k3=h*f(t[i-1]+h*0.5,x[i-1]+0.5*k2)
k4=h*f(t[i-1]+h,x[i-1]+k3)
x[i]=np.array(x[i-1]+(k1+2.0*k2+2.0*k3+k4)/6)
i+=1
return t,x
Zadanie - Wahadło matematyczne z tłumieniem i siłą wymuszającą
Rozwiąż numerycznie metodą RK4 równanie różniczkowe oscylatora harmonicznego z tłumieniem i siłą wymuszającą
[math] \frac{d^2x}{dt^2} + \Gamma \frac{dx}{dt} + w_0^2 x = f_0 \cos(W t) [/math],
przyjmując parametry [math] f_0 =1, w_0=1, \Gamma=0.1, h=0.1 [/math]. Wykreśl zależność amplitudy drgań w funkcji częstości siły wymuszającej W, dla W z przedziału [0.1,3].
Rozwiązanie
Zacznijmy od sprowadzenia równania drugiego stopnia do równania pierszego stopnia i zapisania go w postaci funkcji
def oscylator(t,y):
f0=1.0
w0=1.0
Gamma=0.1
x=y[0]
xdot=y[1]
return np.array([xdot,f0*np.cos(oscylator.W*t)-oscylator.Gamma*xdot-w0*w0*x])
oscylator.W=1.0
Nieprzypadkowo parametr W nie jest definiowany w samej funkcji jako zmienna wewnętrzna, ale jako atrybut obiektu jakim jest funkcja. Dzięki takiej konstrukcji łatwo będzie nam zmieniać parametr W czyli częstość siły wymuszającej. Zobaczmy jak wygląda trajektoria będąca rozwiązaniem tego równania dla warunku początkowego [0,1] i czasu końcowego równego 400.
py.plot(*RK4(oscylator,[0.0,1.0],0.0,400.0,0.1))
py.show()
Widać że początkowo układ dochodzi do stanu regularnych oscylacji. Do analizy amplitudy interesuje nas jedynie koncowa część więc ograniczymy się do analizy trajektorii od czasu 200 do czasu 400. Napiszmy teraz funkcję, która na podstawie trajektorii wyznaczy nam amplitudę oscylacji
def amplituda(x):
lista=x[2000:,0]
return (max(lista)-min(lista))*0.5
Interesować nas będzie amplituda drgań w funkcji częstość W. Wygenerujmy listę wartości W dla których będziemy liczyć amplitudę.
Omegas=np.arange(0.1,3.0,0.05)
Możemy teraz dla każdej z wartości W rozwiązać numerycznie równanie różniczkowe i wyznaczyć odpowiadającą amplitudę oscylacji
amp=[amplituda(RK4(oscylator,[0.0,1.0],0.0,400.0,0.1)[1]) for oscylator.W in Omegas]
Wynik koncowy wyglada następująco
py.plot(Omegas,amp)
py.show()
Jak można było się domyślić amplituda jest największa gdy częstotliwość wymuszania W pokrywa się z wartością częstotliwości drgań własnych [math] w_0=1 [/math]
Zadanie - Układ Lorenza
Rozwiąż układ równań różniczkowych Lorenza dany wzorami
[math] \begin{cases}\dot x=\sigma y-\sigma x\\\dot y=-xz+rx-y\\\dot z=xy-bz\end{cases}, [/math]
metodą całkowania Rungego–Kutty drugiego rzędu z α = 2/3, czyli
[math]k_1 &= f(t_n,x_n)[/math] ,
[math]k_2 &= f(t_n + \tfrac{2}{3}h, x_n + \tfrac{2}{3}h k_1)[/math] ,
[math]x_{n+1} &= x_n + h \left(\tfrac{1}{4}k_1+\tfrac{3}{4} k_2 \right). [/math]
Przyjmij sigma=10, b=8/3, r=99.96, krok czasowy h=0.005 i warunki początkowe x=1,y=0,z=0. Wykonaj 8000 kroków czasowych. Układ po pewnym czasie zacznie poruszać się po pewnej periodycznej trajektorii. Wykonaj 3 rysunki TEJ PERIODYCZNEJ TRAJEKTORII (bez okresu dochodzenia do niej) w płaszczyznach (x,y), (y,z) i (z,x). Wypisz na ekranie przedziały wartości jakie przyjmują zmienne x,y i z na periodycznej trajektorii oraz okres trajektorii periodycznej.
import numpy as np
import pylab as py
#rozwiazujemy rownanie dx(t)/dt=f(t,x)
#metoda Explicit Euler
#f - funkcja f z rownania
#x0-wartosc poczatkowa
#t0-czas poczatkowy
#tk-czas koncowy
#h-krok czasowy
def RK2(f,x0,t0,tk,h):
#generujemy wektor czasow
t=np.arange(t0,tk,h)
#liczba krokow czasowych
N=len(t)
#wektor wynikowy
if hasattr(x0, "__len__"): x=np.zeros((N,len(x0)))
else: x=np.zeros(N)
#wpisujemy wartosc poczatkowa
x[0]=np.array(x0)
#index
i=1
#petla glowna
while (i<N):
k1=h*f(t[i-1],x[i-1])
k2=h*f(t[i-1]+h*2.0/3.0,x[i-1]+k1*2.0/3.0)
x[i]=np.array(x[i-1]+0.25*k1+0.75*k2)
i+=1
return t,x
#uklad Lorenza
def Lorenza(t,y):
sigma=10.0
b=8.0/3
r=99.96
xx=y[0]
yy=y[1]
zz=y[2]
xdot=sigma*(yy-xx)
ydot=-xx*zz+r*xx-yy
zdot=xx*yy-b*zz
return np.array([xdot,ydot,zdot])
t,x=RK2(Lorenza,[1.0,0.0,0.0],0.0,40.0,0.005)
py.plot(x[2500:,0],x[2500:,1])
py.show()
py.plot(x[2500:,1],x[2500:,2])
py.show()
py.plot(x[2500:,2],x[2500:,0])
py.show()
#szukanie okresu
prog=140
lista=[]
for i in range(2500,8000):
if (x[i-1,2]<prog) and (x[i,2]>prog): lista.append(i)
print 'okres to:',np.mean(np.diff(lista)*0.005)
print 'zmienna x przyjmuje wartosci z zakresu: (',min(x[2500:,0]),',',max(x[2500:,0]),')'
print 'zmienna y przyjmuje wartosci z zakresu: (',min(x[2500:,1]),',',max(x[2500:,1]),')'
print 'zmienna z przyjmuje wartosci z zakresu: (',min(x[2500:,2]),',',max(x[2500:,2]),')'