FizykaI FMiN/Zasada Zachowania Energii

Zasada zachowania energii

Praca i energia

Praca

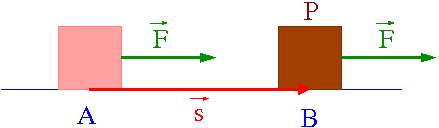
Najprostszy przypadek:

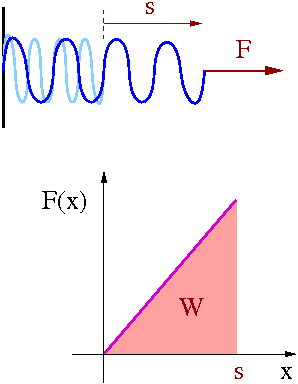
Stała siła [math]\vec{F}[/math] działa na ciało P powodując jego przesunięcie wzdłuż kierunku działania siły o [math]\vec{s}[/math].

Praca jaką wykona przy tym siła [math]\vec{F}[/math]

[math] W_{AB} \; = \; F \cdot s [/math]

W przypadku siły działającej pod kątem w stosunku do przesunięcia praca jaką wykonuje

[math] W_{AB} \; = \; F \cdot s \cdot \cos\theta \; = \; \vec{F} \cdot \vec{s} [/math]

Składowa siły prostopadła do przesunięcia nie wykonują pracy!

Liczy się tylko równoległa składowa siły...

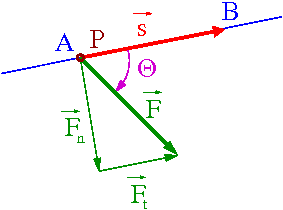
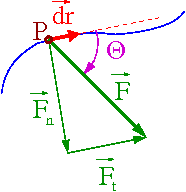
Przypadek ogólny:

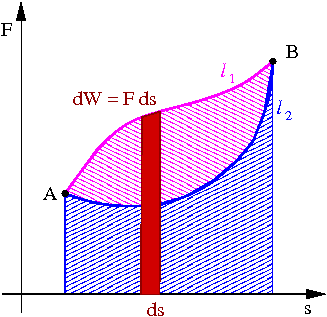
Dowolna siła [math]\vec{F}[/math] działa na punkt materialny P. Praca jaką wykonuje ta siła przy przesunięciu o [math]d \vec{r}[/math] wynosi

[math] d W \; = \; \vec{F} \cdot d \vec{r} \; = \; F \cos\theta d s \; = \; F_t \; d s [/math]

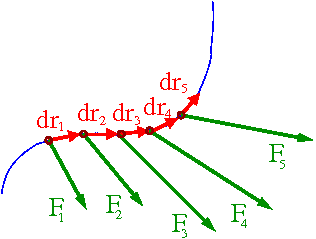
Aby policzyć pracę siły [math]\vec{F}[/math] dla dowolnej drogi, musimy posumować wkłady od kolejnych małych przesunięć [math]d \vec{r}[/math]. W granicy nieskończenie małych przesunięć odpowiada to całkowaniu. Uzyskujemy ogólny wzór na pracę siły [math]\vec{F}(\vec{r})[/math] na drodze między A i B

[math] W_{AB} \; = \; \int\limits_A^B \vec{F}(\vec{r}) \cdot d\vec{r} [/math]

Siły prostopadłe do przesunięcia nie wykonują pracy!

W szczególności nie wykonują pracy poznane już: siła Lorenza, siła Coriolisa i siły reakcji więzów.

Przykład:

Rozciągnięcie sprężyny wymaga wykonania pracy przeciwko sile sprężystości:

[math] F(x) \; = \; k x [/math]

Wykonana praca:

[math] W \; = \; \int\limits_0^s F(x) \cdot dx [/math]

[math] \; = \; \int\limits_0^s k x \cdot dx \; = \; \left[ \frac{1}{2} k x^2 \right]_0^s \; = \; \frac{1}{2} k s^2 [/math]

Graficznie całkę odpowiada polu powierzchni pod wykresem zależności składowej równoległej siły od przesunięcia.

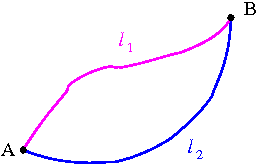
W ogólnym przypadku praca [math]W_{AB}[/math] jaką wykonujemy podczas ruchu punktu z A do B może zależeć od:

• przebytej drogi [math]l[/math]

np. praca sił tarcia będzie proporcjonalna do [math]l[/math]

• toru ruchu

np. jeśli siły oporu zależą od wyboru toru

• prędkości

siły oporu w ośrodku zależą od prędkości

• czasu

jeśli działające siły zależą od czasu

Praca wykonana podczas ruchu z A do B zależy od wybranej drogi [math]l_1[/math] lub [math]l_2[/math]

Energia kinetyczna

Przyjmijmy, że siła [math]\vec{F}[/math] jest siłą wypadkową działającą na ciało P. Zmianę prędkości w ruchu jednostajnie przyspieszonym możemy policzyć znając wartość siły, czas jej działania i masę ciała:

[math] v_B - v_A \; = \; \frac{F}{m} \cdot \Delta t [/math]

[math] \; = \; \frac{F}{m} \cdot \frac{s}{\langle v\rangle } \; = \; \frac{F}{m} \cdot \frac{2s}{v_A + v_B} [/math]

Gdzie skorzystaliśmy z wyrażenia na prędkość średnią w ruchu jednostajnie przyspieszonym: [math]\langle v\rangle = \frac{v_A + v_B}{2}[/math]

Mnożąc obie strony przez [math](v_A + v_B)[/math] otrzymujemy:

[math] v_B^2 -v_A^2 \; = \; (v_B - v_A)(v_B + v_A) \; = \; \frac{2}{m} \cdot F \cdot s \; = \; \frac{2}{m} \cdot W_{AB} [/math]

Pracę wykonana przez siłę podczas ruchu punktu z A do B możemy więc przedstawić jako:

[math] W_{AB} \; = \; \frac{m v_B^2}{2} - \frac{m v_A^2}{2} \; = \; E_k^B - E_k^A \; = \; \Delta E_k [/math]

Wielkość [math]E_k = \frac{m v^2}{2}[/math] wprowadzamy jako energię kinetyczną ciała (w przypadku klasycznym!).

Pracę siły wypadkowej możemy wyrazić poprzez zmianę energii kinetycznej ciała!

W ogólnym przypadku przyczynek do pracy jaką wykonuje siła [math]\vec{F}[/math] od przesunięcia ciała P o małą odległość [math]d s[/math] wynosi

[math] d W \; = \; F_t \; d s \; = \; m \; a_t \; d s \; = \; m \; \frac{dv}{dt} \; d s [/math]

Korzystając z podstawienia [math] \frac{dv}{dt} \; d s \; = \; dv \; \frac{ds}{dt}[/math] uzyskujemy

[math] dW \; = \; m \; \frac{ds}{dt} \; d v \; = \; m \; v \; d v [/math]

Praca siły [math]\vec{F}(\vec{r})[/math] na drodze między A i B wyraża się przez całkę:

[math] W_{AB} \; = \; \int\limits_A^B F_t (s) \cdot ds \; = \; \int\limits_A^B mv \; dv \; = \; \frac{m v_B^2}{2} - \frac{m v_A^2}{2} \; = \; E_k^B - E_k^A \; = \; \Delta E_k [/math]

Niezależnie od postaci siły [math]\vec{F}[/math] i przebytej drogi praca siły jest równa zmianie energii kinetycznej ciała

[math]E_k = \frac{m v^2}{2}[/math]

Zakładamy jedynie, że na ciało nie działają inne siły, a układ, w którym wykonujemy pomiary jest inercjalny.

Moc

Moc średnia opisuje średnią pracę wykonywaną na jednostkę czasu:

[math] P^{^{(śr)}} \; = \; \frac{\Delta W}{\Delta t } [/math]

Moc chwilowa odpowiada mocy liczonej dla nieskończenie małego przedziału czasu

[math] P \; = \; \lim_{\Delta t \rightarrow 0}\; \frac{\Delta W}{\Delta t } \; = \; \frac{dW}{dt} [/math]

Wstawiając wyrażenie na przyrost pracy [math]dW = \vec{F} \cdot d\vec{s} [/math] uzyskujemy ogólny wzór na moc działającej na ciało siły:

[math]P \; = \; \vec{F} \cdot \vec{v} [/math]

Moc siły jest proporcjonalna do prędkości ciała!

Jednostką pracy jest Dżul:

[math] 1 J \; = \; 1 N \cdot 1 m \; = \; 1\; \frac{kg\; m^2}{s^2} [/math]

Jednostką mocy jest Wat:

[math] 1 W \; = \; \frac{1 J}{1 s} \; = \; 1\; \frac{kg\; m^2}{s^3} [/math]

Kiedyś używano jako jednostki mocy konia mechanicznego:

[math] 1\; KM \; = \; 735.498\; W [/math]

Energia potencjalna

Ruch w stałym i jednorodnym polu grawitacyjnym [math]\vec{g}[/math]. Siła ciężkości działająca na masę [math]m[/math]:

[math]\vec{F} = m\;\vec{g} = m\; ( 0, -g , 0 )[/math]

(przyjmujemy, że oś Y układu współrzędnych skierowana jest pionowo do góry).

Praca siły ciężkości przy przesunięciu ciała z A do B

[math] W_{AB} \; = \; \vec{F}\cdot \Delta \vec{r} \; = \; \vec{F} \; ( \vec{r}_B - \vec{r}_A ) [/math]

[math] \; = \; - m \; \vec{g} \; ( \vec{r}_A - \vec{r}_B ) \; = \; m \; g \;(y_A - y_B) [/math]

Możemy wprowadzić energię potencjalną dla jednorodnego pola grawitacyjnego

[math] E_p(\vec{r}) \; = \; -m \; \vec{g} \; \vec{r} \; = \; m \; g \; y [/math]

Pracę możemy wtedy wyrazić przez zmianę energii potencjalnej

[math] W_{AB} \; = \; E_p(\vec{r}_A) \; - \; E_p(\vec{r}_B) \; = \; - \Delta E_p [/math]

Mówimy, że siła ciężkości jest siłą zachowawczą.

Siła [math]\vec{F}(\vec{r})[/math] jest zachowawcza (konserwatywna), jeśli praca przez nią wykonana zależy tylko od położenia punktów początkowego A i końcowego B

Pracę można wtedy wyrazić przez zmianę energii potencjalnej

[math] W_{AB} \; = \; \int\limits_A^B \vec{F}(\vec{r}) \cdot d\vec{r} \; = \; E_p(\vec{r}_A) \; - \; E_p(\vec{r}_B) \; = \; - \Delta E_p [/math]

Siła zachowawcza nie może zależeć od czasu ani od prędkości.

Jeśli droga jest zamknięta to praca siły zachowawczej jest zawsze równa zeru

[math] \int\limits_A^A \vec{F}(\vec{r}) \cdot d\vec{r} \; = \; \oint \vec{F}(\vec{r})d\vec{r} \; = \; 0 [/math]

całkę po drodze zamkniętej nazywamy cyrkulacją (krążeniem) [math]\vec{F}[/math]

Jak pokazaliśmy powyżej siła ciężkości w jednorodnym polu grawitacyjnym jest zachowawcza. Siłami zachowawczymi są też wszystkie siły centralne, zależne tylko od odległości ([math]\vec{F} = F(r) \cdot \vec{i}_r [/math]), w szczególności siła kulombowska, siła grawitacyjna, siły sprężystości...

Siła a energia potencjalna

Praca wykonana przez siłę przy infintezymalnym (nieskończenie małym) przesunięciu [math]d\vec{r} = (dx,dy,dz)[/math]

[math] dW \; = \; \vec{F}(\vec{r}) \cdot d\vec{r}\; = \; -\; d E_p [/math]

Iloczyn skalarny możemy przedstawić poprzez składowe wektorów:

[math] \vec{F} \cdot d\vec{r}\; = \; F_x dx \; + \; F_y dy \; + \; F_z dz [/math]

Zaś zmianę energii potencjalnej przez odpowiednie pochodne cząstkowe: [math] d E_p \; = \; \frac{\partial E_p}{\partial x} \; dx + \frac{\partial E_p}{\partial y} \; dy + \frac{\partial E_p}{\partial z} \; dz [/math]

Porównując te wyrażenia otrzymujemy związek między siłą a energią potencjalną:

[math]\vec{F} = \left( - \frac{\partial E_p}{\partial x}, \; - \frac{\partial E_p}{\partial y}, \; - \frac{\partial E_p}{\partial z} \right) [/math]

Znajomość potencjału siły zachowawczej jest rownoważna znajomości samej siły.

Należy przy tym zauważyć, że energia potencjalna jest określona z dokładnością do stałej, istotne są tylko jej zmiany.

Przykład:

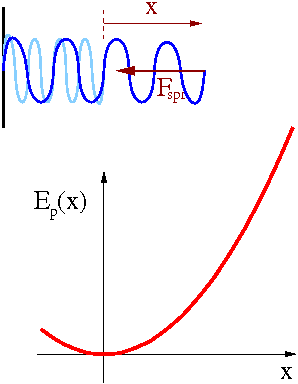
Rozciągnięcie sprężyny wymaga wykonania pracy.

[math] W \; = \; \int\limits_0^s F(x) \cdot dx \; = \; \frac{1}{2} k s^2 [/math]

Kosztem tej pracy rośnie energia potencjalna:

[math] E_p(x) \; = \; \frac{1}{2} k x^2 [/math]

Siła sprężystości:

[math] F_x^{^{spr}} (x) \; = \; - \frac{dE_p(x)}{dx} \; = \; - k x [/math]

W momencie puszczenia sprężyny energia potencjalna zamienia się na kinetyczną...

Gradient

Przedstawioną powyżej funkcję (wektorową) energi potencjalnej:

[math] \vec{\nabla} E_p(\vec{r}) \; = \; \left( \frac{\partial E_p}{\partial x}, \; \frac{\partial E_p}{\partial y}, \; \frac{\partial E_p}{\partial z} \right) [/math]

nazywamy gradientem

Gradient możemy zdefiniować dla dowolnej funkcji skalarnej zależnej od położenia: [math]f(x,y,z)[/math]

[math]\textrm{ grad}\;f \; = \; \vec{\nabla} f \; = \; \vec{i}_x \frac{\partial f}{\partial x} \; + \; \vec{i}_y \frac{\partial f}{\partial y} \; + \; \vec{i}_z \frac{\partial f}{\partial z} \; = \; \left( \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z} \right) [/math]

(używany do oznaczenia gradientu operator [math]\vec{\nabla}[/math] nosi nazwę "nabla")

Gradient wskazuje kierunek w którym następuje największa zmiana wartości funkcji skalarnej [math]f(x,y,z)[/math].

Wartość gradientu odpowiada wartości pochodnej funkcji [math]f(x,y,z)[/math] wzdłuż tego kierunku.

Siłę zachowawczą wyrażamy jako gradient energii potencjalej: [math]\vec{F} = - \vec{\nabla} E_p(\vec{r}) [/math]

Zasada zachowania energii

Energia całkowita

Praca siły zachowawczej [math]\vec{F}(\vec{r})[/math] pomiędzy A i B wyraża się przez energię potencjalną

[math] W_{AB} \; = \; \int\limits_A^B \vec{F}(\vec{r}) \cdot d\vec{r} \; = \; E_p^A - E_p^B [/math]

Z drugiej strony, praca siły działającej na ciało zmienia energię kinetyczną:

[math] W_{AB} \; = \; E_k^B - E_k^A [/math]

Przyrównując te dwa wyrażenia na pracę otrzymujemy:

[math] E_k^B \; - \; E_k^A \; = \; E_p^A \; - \; E_p^B [/math]

[math] E_k^B \; + \; E_p^B \; = \; E_k^A \; + \; E_p^A [/math]

Ale równość ta musi być spełniona dla dowolnych punktów A i B. Wnioskujemy więc, że energia całkowita, będąca sumą energii potencjalnej i kinetycznej pozostaje stała:

[math] E \; = \; E_p \; + \; E_k \; = \; const [/math]

W ruchu pod działaniem sił zachowawczych energia całkowita jest zachowana.

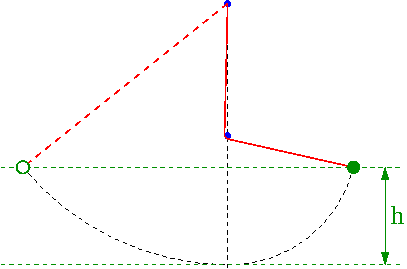
Wahadło Galileusza

Dobrą ilustracją zasady zachowania energii jest tzw. wahadło Galileusza. Gwóźdź wbity poniżej punktu zaczepienia wahadła powoduje, że jego długość ulega efektywnemu skróceniu przy przejściu położenia równowagi. Siły reakcji więzów nie wykonują jednak pracy - nie mają wpływu na bilans energii. Wysokość na jaką wznosi się wahadło nie zmienia się przy zmianie długości nici:

[math]E_p + E_k \; = \; E \; = \; \textrm{const} [/math]

[math] E_k=0 \; \Rightarrow \; m\;g\;h = E [/math]

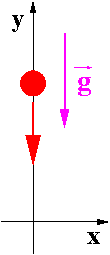
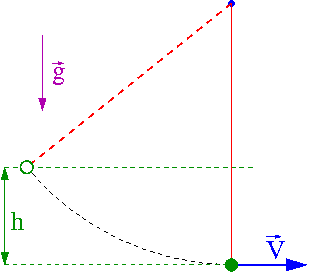
Spadek swobodny

W jednorodnym polu [math]\vec{g}[/math] grawitacyjnym ciało spada swobodnie z wysokości [math]h[/math] ([math]\vec{v}(0)=0[/math]).

Prędkość końcowa z zasady zachowania energii:

[math] \Delta E_k \; = \; - \Delta E_p [/math]

[math] \frac{m \; v^2}{2} \; = \; m \; g \; h [/math]

[math] v \; = \; \sqrt{2 \; g \; h } [/math]

Taką samą prędkość uzyska wahadło puszczone z wysokości [math]h[/math]

Siły sprężystości

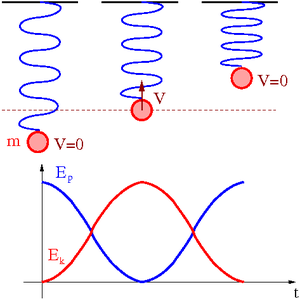
Rozważmy przemiany energii w ruchu kuli o masie [math]m[/math] zawieszonej na sprężynie o współczynniku sprężystości [math]k[/math]. Energia całkowita w ruchu pod wpływem sił sprężystości:

[math] E \; = \; E_p(x) \; + \; E_k(x) \; = \; const [/math]

[math] \frac{1}{2} k x^2 \; + \; \frac{1}{2} m v^2 \; = \; const[/math]

Kula porusza się ruchem harmonicznym z częstością [math]\omega = \sqrt{\frac{k}{m}}[/math]. Zależność położenia od czasu:

[math] x \; = \; A \cdot \sin ( \omega t + \phi ) [/math]

[math] E_p(x) \; = \; \frac{1}{2} k A^2 \sin^2 ( \omega t + \phi ) [/math]

Zależność prędkości od czasu:

[math] v \; = \; \omega \; A \cdot \cos ( \omega t + \phi ) [/math]

[math] E_k(x) \; = \; \frac{1}{2} m \; \omega^2 A^2 \cos^2 ( \omega t + \phi ) [/math]

Podstawiając do wzoru na energię całkowitą:

[math] E \; = \; E_p + E_k \; = \; \frac{1}{2} k A^2 \; = \; const[/math]

Równania ruchu

Znajomość energii potencjalnej jest rownoważna znajomości siły (zachowawczej):

[math]\vec{F} = -\vec{\nabla} E_p [/math]

Czy znając [math] E_p(\vec{r})[/math] możemy rozwiązać równania ruchu ciała ?

• Możemy wyznaczyć zależność [math] \vec{F}(\vec{r})[/math] i skorzystać z II zasady dynamiki...

albo

• Możemy wykorzystać zasadę zachowania energii:

[math] E \; = \; E_k(\dot{\vec{r}}) \; + \; E_p(\vec{r}) \; = \; const [/math]

W zależności od zagadnienia jeden albo drugi sposób może być bardziej użyteczny...

Rozważmy dla uproszczenia przypadek jednowymiarowy: ruchu prostoliniowego pod działaniem siły zachowawczej [math]\vec{F}(x)[/math], energia potencjalna [math]E_p \; = \; E_p(x)[/math]. Zasadę zachowania energii możemy wtedy zapisać w postaci:

[math]E \; = \; \frac{m}{2}\left( \frac{dx}{dt} \right)^2 \; + \; E_p(x) \; = \; const [/math]

co można przekształcić do wyrażenia na prędkość

[math] \frac{dx}{dt} \; = \; \sqrt{\frac{2}{m} \left( E - E_p(x)\right)}[/math]

Rozdzielając zmienne i całkując stronami otrzymujemy:

[math] dt \; = \; \frac{dx}{\sqrt{\frac{2}{m} \left( E - E_p(x)\right)}} [/math]

[math] t \; = \; \int\limits_{x_\circ}^{x} \frac{dx'}{\sqrt{\frac{2}{m} \left( E - E_p(x')\right)}} [/math]

Widzimy więc, że znając [math]E_p(x)[/math] możemy zawsze znaleźć związek między [math]x[/math] i [math]t[/math] (znaleźć ruch ciała).

Przykład:

Ruch pod wpływem stałej siły: [math]\vec{F}=F \; \vec{i}_x = const[/math]

Odpowiada to energii potencjalnej [math]E_p(x) \; = \; - F \; x[/math] ([math]F_x = - \frac{dE_p}{dx}[/math])

Przyjmując, że w chwili początkowej [math]t=0[/math] położenie ciała [math]x=0[/math] mamy:

[math] t \; = \; \sqrt{\frac{m}{2}} \int\limits_{0}^{x} \frac{dx'}{\sqrt{ E +F\;x' }} [/math]

Całkując otrzymujemy:

[math] \sqrt{\frac{2}{m}} \; t \; = \; \frac{2}{F} \left[ \sqrt{ E +F\;x' }\right]_0^{x} \; = \; \frac{2}{F} \sqrt{ E +F\;x } - \frac{2}{F} \sqrt{ E } [/math]

[math] \Rightarrow \qquad \frac{F}{\sqrt{2m}}\; t + \sqrt{E} \; = \; \sqrt{E+F\;x} [/math]

z czego po przekształceniach otrzymujemy

[math] x \; = \; \frac{1}{2} \left( \frac{F}{m} \right) \cdot t^2 \; + \; \sqrt{\frac{2 E}{m}} \cdot t [/math]

[math] \; = \; \frac{1}{2} \;\;\; a \;\;\; \cdot t^2 \; + \;\; v_\circ \;\cdot t [/math]

Widzimy, że ciało porusza się ruchem jednostajnie przyspieszonym.

Jako [math]v_\circ[/math] oznaczyliśmy predkość w chwili [math]t=0[/math]. Wiąże się ona z energią całkowitą (w chwili [math]t=0[/math] położenie [math]x=0[/math] i energia potencjalna znika)

[math] E \; = \; \frac{m v_\circ^2}{2} \gt 0 [/math]

Zderzenia

Poprzednio rozpatrywaliśmy zderzenia ciał z punktu widzenia zasady zachowania pędu (i momentu pędu).

Zasada zachowania pędu jest zawsze bezwzględnie spełniona!

Ale czy w zderzeniach ciał zachowana jest energia kinetyczna?

TAK

jeśli działające siły mają charakter zachowawczy (siły kulombowskie, siły spężystości). Po zderzeniu ciała wracają do tego samego "stanu"

[math]\Delta E_p = 0[/math] ⇒ [math]\Delta E_k = 0[/math]

NIE

jeśli mamy wkład sił niezachowawczych, w szczególności gdy w wyniku zderzenia następują trwałe zmiany (np. odkształcenia) w zderzających się ciałach

Zderzenia sprężyste

Zderzenia, w których zachowana jest energia kinetyczna nazywamy zderzeniami sprężystymi (elastycznymi).

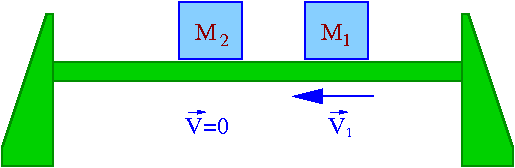
Rozważmy przypadek jednowymiarowy zderzenia dwóch wózków na torze powietrznym (pokaz). Przed zderzeniem przyjmijmy dla uproszczenia, że jeden z wózków spoczywał:

Z zasad zachowania pędu możemy zapisać:

[math] m_1 \; V'_1 \; + \; m_2 \; V'_2 \; = \; m_1 \; V_1 [/math]

natomiast zachowanie energii kinetycznej daje:

[math]\frac{m_1 \; {V'}^2_1}{2} \; + \; \frac{m_2 \; {V'}^2_2}{2} \; = \; \frac{m_1 \; V^2_1}{2} [/math]

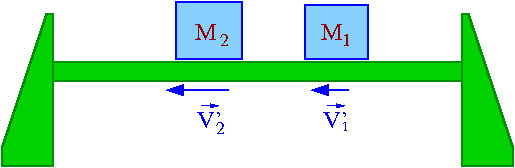
Przekształcając te wyrażenia otrzymujemy

[math] m_2 \; V'_2 \; = \; m_1 \; ( V_1 - V'_1) [/math] (z zachowania pędu)

[math] m_2 \; {V'}^2_2 \; = \; m_1 \; ( V^2_1 - {V'}^2_1) \; = \; m_1 \; ( V_1 - V'_1)( V_1 + V'_1) [/math] (z zachowania energii)

Dzieląc stronami otrzymujemy

[math]V'_2 = V_1 + V'_1[/math]

[math] V'_2 - V'_1 = V_1[/math]

Wartość bezwzględna prędkości względnej ciał przed i po zderzeniu jest taka sama.

Przekształcając dalej otrzymujemy:

[math] m_2 \; ( V_1 + V'_1) \; = \; m_1 \; ( V_1 - V'_1) [/math]

[math] V'_1\; ( m_1 + m_2 ) \; = \; V_1\; ( m_1 - m_2) [/math]

Ostatecznie:

[math]V'_1 \; = \; \frac{ m_1 - m_2}{m_1 + m_2} \; V_1 [/math]

[math]V'_2 \; = \; \frac{ 2\;m_1}{m_1 + m_2} \; V_1 [/math]

Przypadek I

Przypadek szczególny: zderzenie ciał o równej masie [math]m_1 \; = \; m_2[/math]. Otrzymujemy wtedy

[math] V'_1 \; = \; V_2 \;\; = 0 [/math]

[math] V'_2 \; = \; V_1 [/math]

Zderzające się ciała "wymieniają się" prędkościami.

Rozwiązanie takie pozostaje słuszne także w przypadku gdy oba ciała poruszają się przed zderzeniem ([math] \vec{V}_2 \ne 0[/math])

Przypadek II

Rozważmy teraz zderzenie w przypadku [math]m_1 \; \gt \; m_2[/math], czyli gdy masa "pocisku" jest większa od masy "tarczy".

Podstawiając do wyrażeń na prędkość końcową otrzymujemy: [math]V'_2 \gt V'_1 \gt 0[/math]

Po zderzeniu oba ciała poruszają się w tą samą stronę.

Przypadek graniczny: [math]m_1 \; \gg \; m_2[/math]

[math] V'_1 \; = \; \frac{ m_1 - m_2}{m_1 + m_2} \; V_1 \; = \; V_1[/math]

[math] V'_2 \; = \; \frac{2\; m_1}{m_1 + m_2} \; V_1 \; = \; 2 \cdot V_1 [/math]

Tak jak można przypuszczać, ciężki "pocisk" nie zauważa zderzenia z lekką tarczą i kontynuuje lot z niezmienioną prędkością

"Tarcza" uzyskuje prędkość [math]2 \cdot V_1[/math]

Przypadek III

Możliwe jest też zderzenie z [math]m_1 \; \lt \; m_2[/math], czyli gdy masa "pocisku" jest mniejsza od masy "tarczy".

Otrzymujemy wtedy:

[math] V'_1 \; = \; \frac{ m_1 - m_2}{m_1 + m_2} \; V_1 \lt 0 [/math]

[math] V'_2 \; = \; \frac{2\; m_1}{m_1 + m_2} \; V_1 \gt 0 [/math]

Prędkość "pocisku" po zderzeniu zmienia znak. Oznacza to, że "pocisk" odbija się od "tarczy"!

Przypadek graniczny: [math]m_1 \; \ll \; m_2[/math]. Uzyskujemy

[math] V'_1 \; = \; - V_1[/math]

[math] V'_2 \; = \; 0 [/math]

Sprężyste odbicie od "pocisku" od nieruchomej "ściany"

Należy przy tym zwrócić uwagę, że wartość prędkości pocisku nie zmienia się tylko przy odbiciu od nieruchomej "ściany" ([math] V_2 \; = \; 0 [/math]).

Jeśli bardzo ciężka "tarcza" ("ściana") porusza się w kierunku początkowego ruchu "pocisku" to zderzając się z nią "pocisk" traci energię.

Natomiast jeśli "tarcza" przybliża się do "pocisku" w wyniku zderzenia energia "pocisku" rośnie

Jest to mikroskopowy obraz ochładzania (ogrzewania) się gazu przy jego rozprężaniu (sprężaniu) - molekuły gazu tracą lub zyskują energię w zderzeniu z poruszającym się tłokiem.

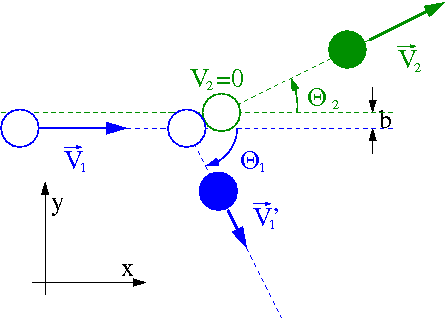
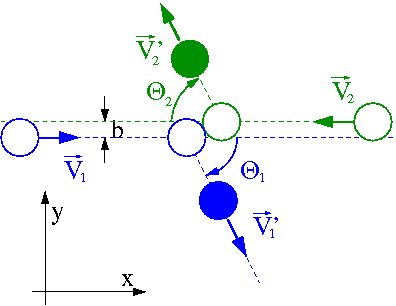
Zderzenia nie centralne

Do tej pory rozpatrywaliśmy tzw. zderzenia centralne, dla których parametr zderzenia [math]b = 0[/math] czyli gdy "pocisk" trafiał w sam środek "tarczy".

W przypadku gdy parametr zderzenia [math]b \ne 0[/math] zderzenie trzeba rozpatrywać w dwóch wymiarach.

Zasada zachowania pędu daje nam dwa równania, na zachowanie składowych X i Y pędu (równoległej i prostopadłej do początkowej prędkości [math]\vec{V}_1 [/math]

[math] p_x[/math]

[math] m_2 \; V'_2 \; \cos \theta_2 \; + \; m_1 \; V'_1 \; \cos \theta_1 \; = \; m_1 \; V_1 [/math]

[math] p_y[/math]

[math] m_2 \; V'_2 \; \sin \theta_2 \; - \; m_1 \; V'_1 \; \sin \theta_1 \; = \; 0 [/math]

Dla zderzeń spężystych możemy też skorzystać z zachowania energii kinetycznej:

[math] \frac{m_1 \; {V'}^2_1}{2} \; + \; \frac{m_2 \; {V'}^2_2}{2} \; = \; \frac{m_1 \; V^2_1}{2} [/math]

Mamy trzy równania na cztery niewiadome ( [math]V'_1[/math], [math]V'_2[/math], [math]\theta_1[/math] i [math]\theta_2[/math]).

Okazuje się, że znajomość [math]m_1[/math], [math]m_2[/math] oraz [math]V_1[/math] i [math]V_2[/math] ([math]V_2=0[/math]) nie wystarcza do wyznaczenia pełnej kinematyki zderzenia!

Musimy ustalić [math]b[/math] albo jeden z parametrów rozproszenia (np. kąt [math]\theta_1[/math]).

Jeśli masy zderzających się sprężyscie ciał są równe [math]m_1 \; = \; m_2[/math] zagadnienie bardzo się upraszcza.

Z zasad zachowania dostajemy wtedy:

[math] \vec{V'}_1 \; + \; \vec{V'}_2 \; = \; \vec{V}_1 [/math]

[math] {V'}^2_1 \; + \; {V'}^2_2 \; = \; V_1^2 [/math]

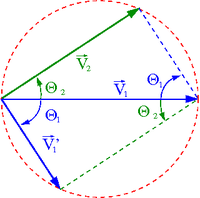
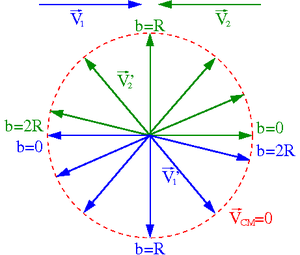
Zauważamy, że wektory [math]\vec{V}_1[/math], [math]\vec{V'}_1[/math] i [math]\vec{V'}_2[/math] tworzą trójkąt prostokątny. Oznacza to, że między kątami rozproszenia zachodzi relacja:

[math] \theta_1 + \theta_2 \; = \; \frac{\pi}{2} [/math]

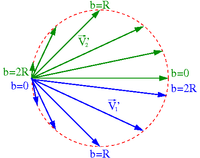
Stan końcowy zależy od parametru zderzenia [math]b[/math]

• [math]b=0[/math] ⇒ zderzenie centralne

[math] \vec{V'}_2 \; = \; \vec{V}_1 [/math]

[math] \vec{V'}_1 \; = \; 0[/math]

• [math]b\gt =2R[/math] ⇒ brak zderzenia (kule mijają się)

[math] \vec{V'}_2 \; = \; 0 [/math]

[math] \vec{V'}_1 \; = \; \vec{V}_1 [/math]

Układ środka masy

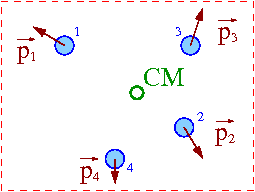
Rozważmy izolowany układ wielu ciał. Zakładamy przy tym, że nasz układ odniesienia jest układem inercjalnym.

Zasada zachowania pędu:

[math] \vec{P} \; = \; \sum_i \vec{p}_i = const [/math]

Środek masy

Klasyczna definicja położenia środka masy:

[math] \vec{R} \; = \; \frac{\sum_i m_i \;\vec{r}_i } {\sum_i m_i } [/math]

Położenie środka masy jest średnią ważoną z położeń [math]\vec{r}_i[/math] poszczególnych składników układu liczoną z wagami [math]w_i = m_i[/math].

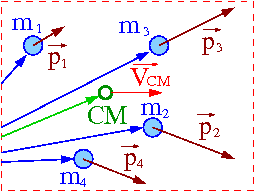
Ruch środka masy (przy założeniu, że masy poszczególnych elementów układu nie ulegają zmianie, [math]m_i[/math]=const) można zapisać jako:

[math] \vec{V}_{CM} \; = \; \frac{d}{dt}\vec{R} \; = \; \frac{\sum_i m_i \;\frac{d}{dt} \vec{r}_i } {\sum_i m_i } [/math]

Mnożąc przez sumę mas:

[math] \left(\sum_i m_i \right) \; \vec{V}_{CM} \; = \; \sum_i m_i \;\vec{v}_i [/math]

[math] M\; \vec{V}_{CM} \; = \; \sum_i \vec{p}_i \; = \; \vec{P} [/math]

Pęd układu możemy związać z ruchem środka masy.

Prędkość środka masy: (klasycznie)

[math] \vec{V}_{CM} \; = \; \frac{\sum_i \vec{p}_i}{\sum_i m_i} \; = \; \frac{\vec{P}}{M} [/math]

Zawsze możemy tak zmienić układ odniesienia, żeby środek masy spoczywał ⇒ układ środka masy (CMS)

Układ środka masy

Układ środka masy jest w wielu przypadkach najwygodniejszym układem odniesienia. Szereg relacji bardzo się w nim upraszcza.

Zasada zachowania pędu w CMS (zmienne w CMS oznaczamy [math]^\star[/math]):

[math]\vec{P}^\star \; = \; \sum_i \vec{p_i}^\star \; = \; 0 [/math]

Jest to jednocześnie ogólna definicja układu środka masy słuszna także w przypadku relatywistycznym ([math]v \sim c[/math])

Zderzenia nie centralne

Porównajmy opis zderzenia nie centralnego w układzie laboratoryjnym i układzie środka masy:

W układzie laboratoryjnym otrzymujemy w ogólnym przypadku skomplikowane wyrażenia na prędkości końcowe w funkcji np. kąta rozproszenia [math]\theta_1[/math] (łatwiej jeśli [math]m_1 = m_2[/math]).

W układzie środka masy rachunki bardzo się upraszczają. Z zasady zachowania pędu (definicja układu środka masy):

[math]\vec{P}^\star = 0[/math]

uzyskujemy wprost związki między prędkościami i kątami rozproszenia ciał:

[math]\theta_1 \; = \; \theta_2 [/math]

[math] \frac{V_1}{V_2} \; = \; \frac{V'_1}{V'_2} \; = \; \frac{m_2}{m_1} [/math]

Wstawiając związek między prędkościami [math]V_2 = \frac{m_1}{m_2} V_1[/math] do wyrażenia na energię kinetyczną otrzymujemy z zasady zachowania energii

[math] \frac{m_1 V_1^2}{2} \; + \; \frac{m_2 V_2^2}{2} \; = \; \frac{m_1 {V'}^2_1}{2} \; + \; \frac{m_2 {V'}^2_2}{2} [/math]

[math] \left( m_1 + \frac{m_1^2}{m_2} \right)V_1^2 \; = \; \left( m_1 + \frac{m_1^2}{m_2} \right){V'}^2_1 [/math]

Czyli

[math] V'_1 = V_1[/math] i [math]V'_2 = V_2 [/math]

W układzie środka masy (!) niezależnie od mas zderzających się ciał, wartości ich prędkości przed i po zderzeniu sprężystym są takie same.

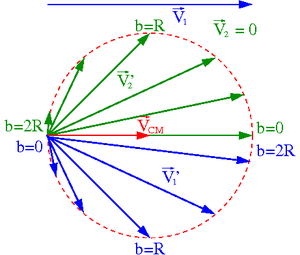
Przypadek [math]m_1 \; = \; m_2[/math]

Układ środka masy	Układ laboratoryjny

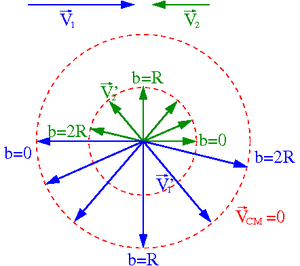
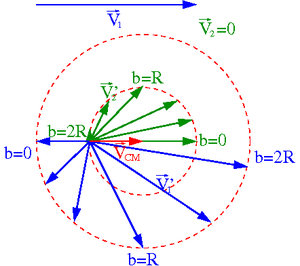
Przypadek [math]m_1 \; \lt \; m_2[/math]

Układ środka masy	Układ laboratoryjny

Rysunki wykonano dla [math]m_1 = \frac{1}{2} m_2[/math].

⇒ [math]v_1 = 2 \; v_2[/math] w układzie środka masy

⇒ [math]V_{CM} \; = \; \frac{1}{3} \; V_1[/math] w układzie laboratoryjnym

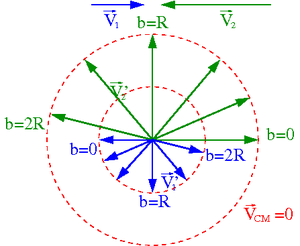
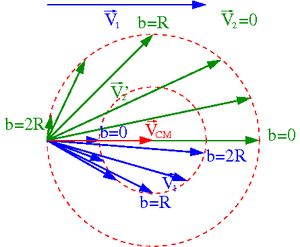
Przypadek [math]m_1 \; \gt \; m_2[/math]

Układ środka masy	Układ laboratoryjny

Rysunki wykonano dla [math]m_1 = 2\; m_2[/math].

⇒ [math]v_1 = \frac{1}{2} v_2[/math] w układzie środka masy

⇒ [math]V_{CM} \; = \; \frac{2}{3} \; V_1[/math] w układzie laboratoryjnym

Korzystając z definicji środka masy mamy związek między wartościami prędkości:

[math] V_{CM} \; = \; v_2^\star \; = \; \frac{m_1}{m_1 + m_2} \; V_1 [/math]

[math] v_1^\star \; = \; \frac{m_2}{m_1} v_2^\star \; = \; \frac{m_2}{m_1 + m_2} \; V_1 [/math]

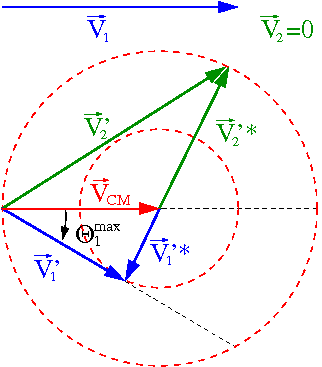
Wektory prędkości tworzą trójkąt (patrz rysunek):

[math] \vec{V'}_{1} \; = \; \vec{V}_{CM} \; + \; \vec{V'}_{1}^\star [/math]

Kąt rozproszenia "pocisku" w układzie laboratoryjnym będzie maksymalny, gdy będzie to trójkąt prostokątny (patrz rysunek obok):

[math] \sin \theta_1^{max} \; = \; \frac{v_1^\star}{V_{CM}} \; = \; \frac{m_2}{m_1} [/math]

Jeśli [math]m_1 \; \gt \; m_2[/math] "pocisk" rozprasza się w ograniczonym przedziale kątów

[math] 0 \; \lt \; \theta_1 \; \lt \; asin\left(\frac{m_2}{m_1}\right) [/math]

Natomiast dla "tarczy" ograniczenie nie zależy od stosunku mas:

[math] 0 \; \lt \; \theta_2 \; \lt \; \frac{\pi}{2} [/math]

Energia układu

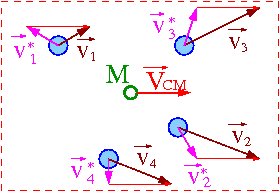
Rozważmy ponownie izolowany układ wielu ciał (opisywany w inercjalnym układzie odniesienia). Transformacja prędkości z układu środka masy do układu laboratoryjnego:

[math] \vec{v}_i \; = \; \vec{v_i}^\star \; + \; \vec{V}_{CM} [/math]

Energia kinetyczna układu:

[math] E_k \; = \; \sum_i \frac{m_i \; v_i^2}{2} \; = \; \sum_i \frac{m_i \; |\vec{v_i}^\star +\vec{V}_{CM} |^2}{2} [/math]

[math] = \; \sum_i \left( \frac{m_i \; (v_i^\star)^2}{2} + 2 \frac{m_i \; \vec{v_i}^\star \vec{V}_{CM}}{2} + \frac{m_i \; {V}_{CM}^2}{2} \right) [/math]

Z zasady zachowania pędu:

[math] \sum_i m_i \; \vec{v_i}^\star \vec{V}_{CM} \; = \; \vec{V}_{CM} \sum_i m_i \; \vec{v_i}^\star = \vec{V}_{CM} \; \vec{P}^\star = 0 [/math]

Ostatecznie więc otrzymujemy:

[math]E_k \; = \; E_k^\star \; + \; \frac{M \; {V}_{CM}^2}{2} [/math]

Energia kinetyczna układu jest sumą energii "wewnętrznej" ([math]E_k^\star[/math]) i energii kinetycznej układu jako całości.

Moment pędu układu

Transformacja galileusza:

[math] \vec{r}_i \; = \; \vec{r_i}^\star \; + \; \vec{R}_{CM} [/math]

[math] \vec{v}_i \; = \; \vec{v_i}^\star \; + \; \vec{V}_{CM} [/math]

Całkowity moment pędu względem początku układu

[math] \vec{L} \; = \; \sum_i m_i \; \vec{r}_i \times \vec{v}_i [/math]

[math] \; = \; \sum_i m_i \left( \vec{R}_{CM} + \vec{r_i}^\star \right) \times \left( \vec{V}_{CM} + \vec{v_i}^\star \right) [/math]

[math] \; = \; \left[ \sum_i m_i \right] \vec{R}_{CM} \times \vec{V}_{CM} \; + \; \vec{R}_{CM} \times \sum_i m_i \vec{v_i}^\star [/math]

[math] \; \; \; + \; \left[ \sum_i m_i \vec{r_i}^\star \right] \times \vec{V}_{CM} \; + \; \sum_i m_i \vec{r_i}^\star \times \vec{v_i}^\star [/math]

Z definicji CMS:

[math]\sum m_i \vec{v_i}^\star = \sum m_i \vec{r_i}^\star = 0 [/math]

otrzymujemy:

[math]\vec{L} \; = \; M \vec{R}_{CM} \times \vec{V}_{CM} \; + \; \vec{L}_{CM}^\star [/math]

Moment pędu układu jest sumą "wewnętrznego" momentu pędu ([math]\vec{L}_{CM}^\star[/math]) (liczonego względem środka masy) i momentu pędu układu jako całości.

Ruch środka masy

Dla układu izolowanego

[math]\vec{P} \; = \; \textrm{const} [/math]

środek masy pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym.

⇒ dla układu jako całości spełniona jest I Zasada Dynamiki

Pod działaniem sił zewnętrznych:

[math]\vec{F}^{zw} \; = \; \sum_i \vec{F}_i^{zw} [/math]

zmiana pędu układu:

[math]\frac{d \vec{P}}{dt} \; = \; \sum_i \frac{d \vec{p}_i}{dt} [/math]

[math] \; = \; \sum_i \vec{F}_i^{zw} \;+\; \sum_i \sum_j \vec{F}_{ij} \; = \; \vec{F}^{zw} [/math]

⇒ spełniona II~ Zasada Dynamiki

W oparciu o pojęcie środka masy możemy opisać ruch układu jako całości stosując równania ruchu punktu materialnego.