FizykaI FMiN/Bryła sztywna 2

Bryła sztywna (2)

Bąk

Równowaga

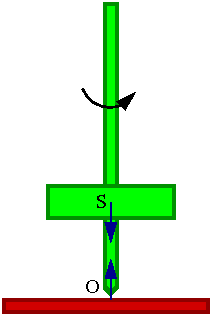
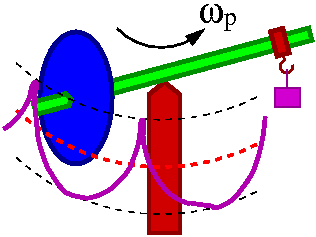
Rozważmy bąk podparty wirujący do okoła pionowej osi. Z zasady zachowania mementu pędu wynika, że jeśli zapewnimy znikanie momentów sił to kierunek momentu pędu pozostanie stały niezależnie od działających sił i ruchu postępowego. Zjawisko to nosi nazwę efektu żyroskopowego.

Bąk wirujący wokół pionowej osi jest w równowadze. Momenty działających sił są równe zero (zarówno względem środka masy S jak i punktu podparcia O).

Moment pędu jest więc stały, jeśli przyjmiemy, że bąk jest symetryczny stała będzie też orientacja osi obrotu

[math] \vec{L} \; = \; \vec{\omega} \; I \; = \; const [/math]

Czy jest to równowaga trwała?

Moment sił

Gdyby bąk nie wirował ([math]L=0[/math]) to ustawienie pionowe byłoby stanem równowagi nietrwałej.

Wychylenie z tego położenia powodowałoby powstanie wypadkowego momentu sił oraz niezerowej siły wypadkowej, które powodowałyby wywrócenie bąka.

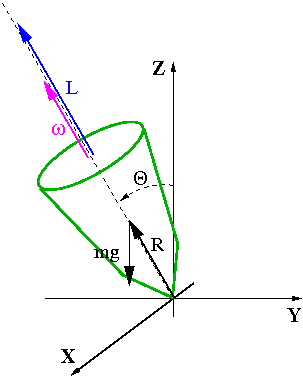
Rozważmy wirujący bąk, którego oś jest nachylona do kierunku pionowego.

Moment siły ciężkości względem punktu podparcia O dany jest przez:

[math]\vec{M} \; = \; \vec{R} \times m \vec{g} [/math]

a wartość momentu siły ciężkości:

[math] M \; = \; m g R \; \sin \theta [/math]

gdzie [math]R[/math] - odległość środka ciężkości od punktu podparcia

[math]\theta[/math] - kąt odchylenia osi od pionu

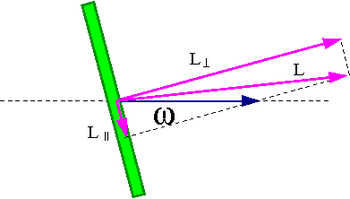
Moment siły [math]\vec{M}[/math] skierowany jest poziomo, prostopadle do osi bąka (kierunku [math]\vec{R}[/math]) i kierunku siły ciężkości.

Precesja

W przypadku gdy bąk wiruje, przyłożony moment siły powoduje zmianę całkowitego momentu pędu:

[math] \vec{M} \; = \; \frac{d\vec{L}}{dt} [/math]

Zakładamy, że wektor momentu pędu pokrywa się z osią obrotu

[math]\vec{L} \parallel \vec{\omega} \parallel \vec{R}[/math]

natomiast wektor momentu siły jest zawsze do niej prostopadły

[math]\vec{M} = m \vec{R} \times \vec{g} \; \perp \; \vec{R}[/math]

Tym samym działający moment siły nie zmienia wartości momentu pędu, wartość ta pozostaje stała

[math] \frac{dL}{dt} \; = \; 0 [/math]

Zmienia się natomiast kierunek momentu pędu, a więc i kierunek osi obrotu. Zjawisko to nazywamy precesją.

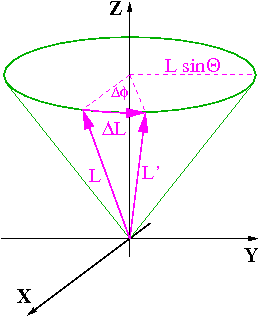
W małym przedziale czasu [math]\Delta t[/math] moment pędu zmieni się o:

[math] \Delta L \; = \; M \; \Delta t \; = \; m R g \; \sin \theta \; \Delta t [/math]

Zmiana ta będzie skierowana poziomo, prostopadła do kierunku momentu pędu. Spowoduje to obrót poziomej składowej [math]\vec{L}[/math] o kąt

[math] \Delta \phi \; = \; \frac{\Delta L}{L \; \sin \theta} \; = \; \frac{ m R g \; \sin \theta }{L \; \sin \theta} \; \Delta t [/math]

Częstość z jaką wektor [math]\vec{L}[/math] będzie zakreślał stożek, czyli częstość precesji, dana jest więc wzorem:

[math] \omega_p \; = \; \frac{\Delta \phi}{\Delta t } \; = \; \frac{ m R g }{L } [/math]

Częstość precesji maleje ze wzrostem momentu pędu (częstości ruchu wirowego bąka) - im szybciej bąk wiruje tym wolniej zmienia się kierunek [math]\vec{L}[/math].

Częstość precesji nie zależy od kąta pochylenia osi bąka!

Żyroskop

Równowaga

Żyroskop w równowadze

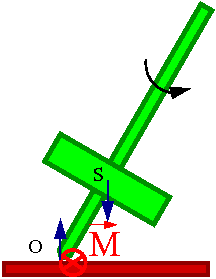
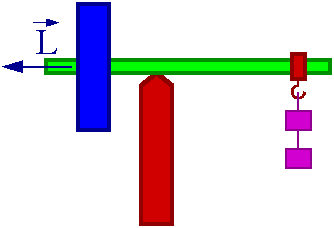
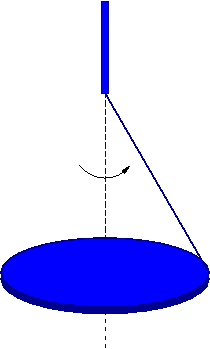
Żyroskop jest to oś mogąca swobodnie zmieniać swój kierunek w przestrzeni i wirująca wokół tej osi bryła (najczęściej obręcz lub dysk).

Żyroskop który wykorzystaliśmy na wykładzie przypominał wagę: ciężar obracającego się dysku jest zrównoważona przez odpowiednio dobrane ciężarki (patrz rysunek).

Jeśli żyroskop jest w równowadze przy [math]\vec{L}=0[/math] to będzie także w równowadze dla [math]\vec{L} \ne 0[/math]

Precesja

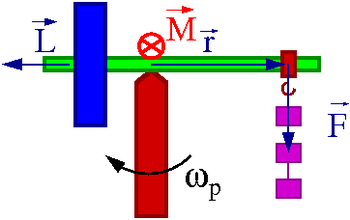
Jak zachowa się żyroskop gdy zwiększymy lub zmniejszymy "przeciwwagę" ?

Zwiększone obciążenie

Zmniejszone obciążenie

W obu przypadkach nastąpi precesja, czyli obrót osi obrotu żyroskopu w płaszczyźnie poziomej.

Jeśli obciążenie zostanie

zwiekszone

precesja zgodnie z ruchem wskazówek zegara (patrząc os góry)

zmniejszone

precesja przeciwnie do ruchu wskazówek zegara (odpowiada to precesji bąka)

Częstość precesji żyroskopu

[math] \omega_p \; = \; \frac{ \Delta m \; r \; g }{L } [/math]

jest proporcjonalna do dodanej lub brakującej masy

Paradoks ?

Nie wirujący bąk ([math]\vec{L}=0[/math]) wychylony z położenia równowagi wywraca się. Także nie zrównoważony żyroskop, jeśli nie jest rozkręcony ([math]\vec{L}=0[/math]) opada.

Z drugiej strony doświadczenie pokazuje, że jeśli [math]\vec{L} \ne 0[/math] to bąk i żyroskop podlegają precesji i (zaniedbując siły tacia) nigdy się nie wywrócą.

Czy jest to słuszne dla dowolnie małych wartości [math]\vec{L}[/math] ?

Z doświadczenia wiemy, że nie ! Wirujący bąk wywraca się zanim prędkość kątowa jego ruchu wirowego spadnie do zera.

Nasze dotychczasowe rozważania precesji nie były ścisłe, dla małych momentów pędu musimy uwzględnić dodatkowe efekty...

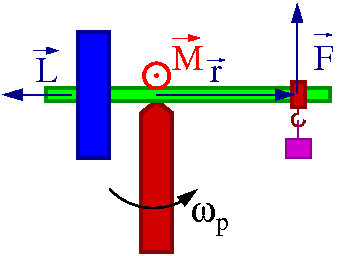
Niech moment pędu zrównoważonego żyroskopu wynosi [math]\vec{L}[/math].

Co się dzieje gdy zdejmiemy jeden ciężarek ?

Wartość całkowitego moment pędu nie ulega zmianie, gdyż moment siły ciężkości jest prostopadły do [math]\vec{L}[/math].

Powoduje jednak obrót żyroskopu z częstością [math]\omega_p[/math] względem pionowej osi. Ale oznacza to pojawienie się dodatkowej składowej momentu pędu związanej z tym obrotem

[math]\vec{L}_p = \omega_p \; I_p[/math]

Aby całkowity moment pędu nie uległ zmianie, oś żyroskopu musi się nachylić o kąt:

[math] \theta \sim \frac{L_p}{L} = \frac{mrg I_p}{L^2} [/math]

Jeśli moment pędu [math]L[/math] jest duży to kąt ten [math]\theta \rightarrow 0[/math] i [math]L_p[/math] można pominąć.

Jednak gdy pod wypływem oporów ruchu prędkość wirowania spada, [math]L[/math] maleje, żyroskop/bąk wywraca się...

Nutacja

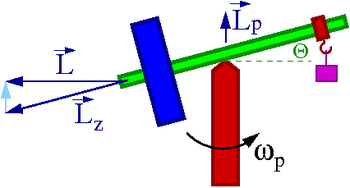
Nutacja

Idealna precesja, gdy koniec ramienia żyroskopu porusza się ruchem jednostajnym po okręgu, zachodzi tylko przy szczególnym wyborze warunków początkowych.

W ogólnym przypadku na precesję nakładają się oscylacje ramienia żyroskopu wokół położenia "stacjonarnej precesji". Nazywamy je nutacją.

Charakter tych dodatkowych oscylacji zależy od warunków początkowch. Zazwyczaj są mało widoczne i szybko zanikają w czasie (tłumienie związane z oporami ruchu). Ich amplituda rośnie dla małych wartości [math]L[/math]

Tensor momentu bezwładności

Moment pędu

Do tej pory rozpatrywaliśmy wyłącznie ruch obrotowy bryły względem ustalonej osi. Naogół była to oś symetrii bryły, lub oś do niej równoległa. Jednak w ogólnym przypadku problem jest dużo bardziej skomplikowany

Przykład I

Rozważmy dwa ciężarki przymocowane do wirującej osi.

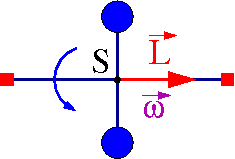
Jeśli ciężarki są zamocowane symetrycznie, w jednej płaszczyźnie prostopadłej do osi obrotu, to oś obrotu jest osią symetrii bryły i moment pędu będzie równoległy do osi obrotu

[math] \vec{L} \parallel \vec{\omega}[/math]

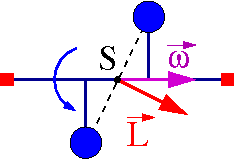
Jeśli jednak ciężarki będą rozsunięte wzdłuż osi obrotu to oś ta nie będzie się pokrywała z osią symetrii. Moment pędu

[math]\displaystyle \vec{L}_i = m_i \vec{r}_i \times \vec{v}_i [/math]

będzie prostopadły do wektorów opisujących pozycję ciężarków względem środka ciężkości [math]\vec{r}_i[/math] więc nie będzie równoległy do osi obrotu

[math] \vec{L} \nparallel \vec{\omega}[/math]

Przykład II

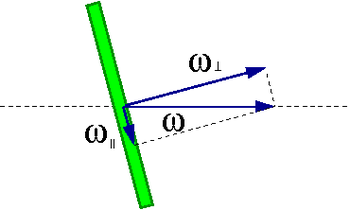
Rozważmy dysk wirujący wokół osi nachylonej do osi symetrii

Prędkość kątową możemy rozłożyć na składową równoległą i prostopadła do osi symetrii

[math] \vec{\omega} \; = \; \vec{\omega}_\perp \; + \; \vec{\omega}_\parallel [/math]

Moment bezwładności dysku jest różny dla obrotu wokół osi symetrii i wokół osi do niej prostopadłej:

[math] I_\perp = \frac{1}{2} m r^2 [/math]

[math] I_\parallel = \frac{1}{4} m r^2 \; = \; \frac{1}{2}\; I_\perp [/math]

Moment pędu dysku możemy policzyć osobno dla każdej składowej

[math] \vec{L} \; = \; \vec{L}_\perp \; + \; \vec{L}_\parallel [/math]

[math] \; = \; I_\perp \vec{\omega}_\perp \; + \; I_\parallel \; \vec{\omega}_\parallel [/math]

[math] \; = \; I_\perp \left( \vec{\omega}_\perp \; + \; \frac{1}{2}\vec{\omega}_\parallel \right) [/math]

Widzimy, że kierunek momentu pędu różny jest od kierunku prędkości kątowej jeśli tylko nie jest ona skierowana równolegle lub prostopadle do osi symetrii

[math] \vec{L} \nparallel \vec{\omega}[/math]

Definicja tensora

W ogólnym przypadku bryła sztywna może nie mieć żadnej osi symetrii. Jak wtedy wyznaczyć moment pędu, znając prędkość kątową [math]\vec{\omega}[/math] ?

Zdefinicji momentu pędu:

[math] \vec{L} \; = \; \sum_i m_i \vec{r}_i \times \vec{v}_i[/math]

Z definicji bryły sztywnej:

[math] \vec{v}_i \; = \; \vec{\omega} \times \vec{r}_i[/math]

Otrzymujemy:

[math] \vec{L} \; = \; \sum_i m_i \vec{r}_i \times \left( \vec{\omega} \times \vec{r}_i\right) \; = \; \sum_i m_i \left[ \vec{\omega} \; r_i^2 - \vec{r}_i \; ( \vec{r}_i \; \vec{\omega} ) \right] [/math]

gdzie korzystamy z tożsamości wektorowej:

[math]\vec{A} \times \left( \vec{B} \times \vec{C} \right) = \vec{B} \left( \vec{A} \cdot \vec{C} \right) - \vec{C} \left( \vec{A} \cdot \vec{B} \right) [/math]

Widzimy więc, że kierunek [math]\vec{L}[/math] zależy od kierunku [math]\vec{\omega}[/math] jak i położeń poszczególnych elementów bryły opisanych przez [math]\vec{r}_i[/math].

Rozpisując na składowe:

[math] \vec{r}_i \; = \; (x_i, y_i, z_i) [/math]

[math] \vec{\omega} \; = \; (\omega_x, \omega_y, \omega_z) [/math]

[math] \vec{r}_i \; \vec{\omega} \; = \; x_i\omega_x + y_i\omega_y + z_i\omega_z [/math]

Otrzymujemy (na przykładzie [math]L_x[/math]):

[math] L_x \; = \; \sum_i m_i \left[ \omega_x \; r_i^2 - x_i \; ( x_i\omega_x + y_i\omega_y + z_i\omega_z ) \right] [/math]

[math] \; = \; \omega_x \cdot \sum_i m_i (r_i^2 -x_i^2) \; - \; \omega_y \cdot \sum_i m_i \; x_i y_i \; - \; \omega_z \cdot \sum_i m_i \; x_i z_i [/math]

Widzimy, że [math]L_x[/math] zależy w ogólności od waszystkich skladowych prędkości kątowej!

Podobnie:

[math] L_y \; = \; - \; \omega_x \cdot \sum_i m_i \; x_i y_i \; + \; \omega_y \cdot \sum_i m_i (r_i^2 -y_i^2) \; - \; \omega_z \cdot \sum_i m_i \; y_i z_i [/math]

[math] L_z \; = \; - \; \omega_x \cdot \sum_i m_i \; x_i z_i \; - \; \omega_y \cdot \sum_i m_i \; y_i z_i \; + \; \omega_z \cdot \sum_i m_i (r_i^2 -z_i^2) [/math]

Wyrażenie na składowe [math]\vec{L}[/math] możemy zapisać w postaci macierzowej:

[math] \vec{L} \; = \; \left( \begin{array}{c} L_x \\ L_y \\ L_z \end{array} \right) \; = \; \left( \begin{array}{ccc} \sum m_i (r_i^2 -x_i^2) & - \sum m_i \; x_i y_i & - \sum m_i \; x_i z_i \\ - \sum m_i \; x_i y_i & \sum m_i (r_i^2 -y_i^2) & -\sum m_i \; y_i z_i \\ - \sum m_i \; x_i z_i & - \sum m_i \; y_i z_i & \sum m_i (r_i^2 -z_i^2) \end{array} \right) \cdot \left( \begin{array}{c} \omega_x \\ \omega_y \\ \omega_z \end{array} \right)[/math]

gdzie wprowadzoną macierz nazywamy tensorem momentu bezwładności i oznaczamy [math]\hat{I}[/math]

[math]\vec{L} = \hat{I} \cdot \vec{\omega} [/math]

Składowe tensora momentu bezwładności to współczynniki bezwładności

[math] \hat{I} \; = \; \left( \begin{array}{ccc} I_{xx} & I_{xy} & I_{xz} \\ I_{yx} & I_{yy} & I_{yz} \\ I_{zx} & I_{zy} & I_{zz} \end{array} \right) [/math]

Ogólny wzór na współczynnik bezwładności ma postać ([math]u,v \; = \; x, y, z[/math])

[math] I_{uv} \; = \; \sum m_i ( \delta_{uv} \; r_i^2 \; - \; u_i v_i) [/math]

lub (w przypadku ciągłego rozkładu masy)

[math] I_{uv} \; = \; \int dV \rho(\vec{r}) ( \delta_{uv} \; r^2 \; - \; u\; v) [/math]

gdzie [math]\delta_{uv}[/math] to tzw. delta Kroneckera:

[math]\delta_{uv} = \; 1[/math] dla [math]u=v[/math]

[math]\delta_{uv} = \; 0[/math] dla [math]u\ne v[/math]

Przykład

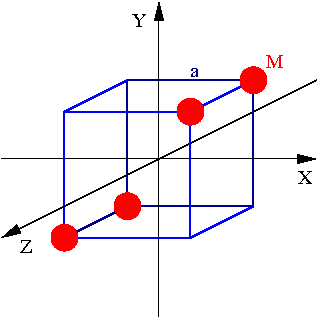
Cztery masy rozmieszczone w rogach sześcianu:

Tensor momentu bezwładności wynosi

[math] \hat{I} \; = \; \left( \begin{array}{rrr} 2 & -1 & 0 \\ -1 & 2 & 0 \\ 0 & 0 & ~~2 \end{array} \right) \cdot M \; a^2 [/math]

Osie główne

W ogólnym przypadku wszystkie współczynniki bezwładności mogą być różne od zera (tensor jest symetryczny ⇒ 6 niezależnych wielkości)

Okazuje się jednak, że w każdym przypadku można tak obrócić osie układu odniesienia, żeby elementy pozadiagonalne znikały (diagonalizacja tensora):

[math] I_{xy} = I_{xz} = I_{yz} = I_{yx} = I_{zx} = I_{zy} = 0 [/math]

Układ w którym tensor momentu bezwładności jest diagonalny definiuje nam osie główne bryły (kierunki własne tensora)

Jeśli bryła ma oś symetrii to będzie ona jedną z osi głównych !

Po diagonalizacji pozostają tylko 3 współczynniki diagonalne [math]I_{xx}[/math], [math]I_{yy}[/math], [math]I_{zz}[/math] (wartości własne tensora)

W układzie osi głównych wyrażenie na moment pędu

[math] \vec{L} = (L_x, L_y, L_z) \; = \; (I_{xx} \; \omega_x ,\; I_{yy} \; \omega_y,\; I_{zz} \; \omega_z)[/math]

Dla obrotu wokół osi głównej moment pędu jest zawsze równoległy do osi obrotu

[math]\vec{L} \parallel \vec{\omega}[/math]

np. [math]\vec{\omega} = (\omega, 0, 0 )[/math] ⇒ [math]\vec{L} = (I_{xx} \omega, 0, 0 ) = I_{xx} \vec{\omega}[/math]

Przykład

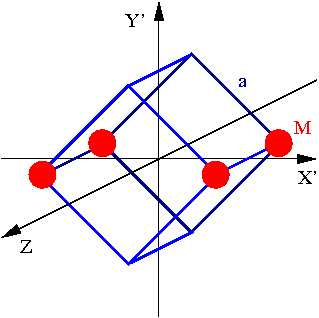
Dla czterech mas rozmieszczone w rogach sześcianu osie główne odpowiadają osiom symetrii wyznaczonego przez te masy prostokąta

Tensor bezwładności w układzie osi głównych:

[math] \hat{I} \; = \; \left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 2 \end{array} \right) \cdot M \; a^2 [/math]

Osie X', Y' i Z są osiami głównymi [math]\hat{I}[/math]:

• oś X' - najmniejszy moment bezwładności
• oś Y' - największy moment bezwładności
• oś Z - pośredni moment bezwładności

Bryła swobodna

W przypadku bryły wirującej swobodnie (stała wartość [math]\vec{L}[/math]) stabilny ruch obrotowy (stały kierunek wektora [math]\vec{\omega}[/math]) możliwy jest tylko wokół osi głównych o największym i najmniejszym momencie bezwładności!

W przypadku obrotu wokół osi głównej o pośrednim momencie bezwładności ruch będzie niestabilny (odpowiada to równowadze chwiejnej).

Energia kinetyczna w układzie osi głównych:

[math] E_k = \frac{1}{2} \vec{\omega} \vec{L} = \frac{1}{2} (I_{xx} \omega_x^2 + I_{yy} \omega_y^2 + I_{zz} \omega_z^2 )[/math]

Jeśli więzy narzucają obrót ze stała prędkością kątową [math]\vec{\omega}[/math] to ciało przyjmie ułożenie odpowiadające maksymalnej energii kinetycznej, czyli obraca się wokół osi o największym momencie bezwładności. Odpowiada to też maksymalnej wartości momentu pędu.

W układzie obracającym się siła odśrodkowa dąży do rozmieszczenia masy jak najdalej od osi obrotu. Stabilny jest stan odpowiadający minimum energii potencjalnej (siły odśrodkowej).

Siła odśrodkowa

[math] \vec{F}_i \; = \; m_i \; \omega^2 \vec{r}_{i \perp} [/math]

odpowiadająca jej energia potencjalna wyraża się więc wzorem

[math] E_{p, i} \; = \; - \frac{1}{2} \; m_i \; \omega^2 \; r_\perp^2 \; = \; - E_{k, i} [/math]

Minimum energii potencjalnej odpowiada maksimu energii kinetycznej.

W układzie laboratoryjnym masa "oddala się" od osi zgodnie z zasadą bezwładności.