Obrazowanie:Obrazowanie Medyczne/Oddziaływanie Promieniowania Elektromagnetycznego z Materią

Oddziaływanie Promieniowania Elektromagnetycznego z Materią

Przekrój Czynny

Schemat tarczy (kolor szary), zawierającej centra oddziaływania (czerwone koła), na której rozproszona zostaje wiązka promieniowania.

W pierwszym rozdziale zostało zdefiniowane pojęcie obrazu jako odwzorowania pewnej cechy obiektu na płaszczyznę. Najczęściej wymienianą cecha tego obiektu, podawaną w przykładach, była jego jasność. Tworzenia obrazu wnętrza ciała ludzkiego wymaga zastosowania promieniowania o innych właściwościach niż mają je fale elektromagnetyczne z zakresu widzialnego. Promieniowanie to musi mieć zdolność penetracji ciała ludzkiego oraz oddziaływania z materią, z którego jest ono zbudowane. W zależności od rodzaju promieniowania i jego energii, może ono w różny sposób oddziaływać z materią. W związku z tym niezbędne jest określenie prawdopodobieństwa zajścia poszczególnych procesów oddziaływania. W celu wyznaczenia tego prawdopodobieństwa wprowadza się pojęcie przekroju czynnego. Przypominamy, iż w fizyce jądrowej operuje się miarą przekroju czynnego oraz różniczkowego przekroju czynnego. Ta ostania wielkość nie jest stosowana w obrazowaniu medycznym, dlatego pominiemy ją dalszej części rozdziału.
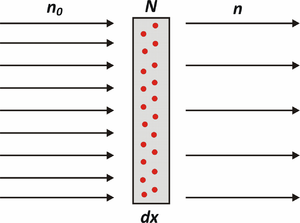
Rozważmy tarczę o powierzchni S i grubości x, która zawiera tzw. centra oddziaływania (mogą to być jądra atomowe, czy też elektrony). Na tarczę pada strumień n cząstek. Interesuje nas, ile cząstek zdoła pokonać tarczę. W tarczy znajdują się obiekty - centra oddziaływania, którymi mogą być jądra atomowe, lub też elektrony. Oznaczmy przez N gęstość centrów oddziaływania (ich liczbę na jednostkę objętości). Rozpatrzmy teraz, ile cząstek przejdzie bez oddziaływania przez cienką warstwę tarczy [math]\Delta x[/math]. Skoncentrowaliśmy się na cienkim pasku, bowiem w takim przypadku możemy założyć, iż centra oddziaływania nie przesłaniają się. Każde centrum oddziaływania posiada pewną powierzchnię [math]\sigma[/math] (prostopadłą do kierunki padającej wiązki), w obrębie której wywiera jakieś oddziaływanie na cząstki. Stosunek liczby cząstek, które uległy oddziaływaniu z centami do liczby wiązek w cząstce opisuje następujące wyrażenie:

[math] \Delta n = -\frac{S\Delta xN\sigma}{S}n. [/math]

Dokonajmy pewnych przekształceń na powyższym równaniu:

[math] \begin{array}{l} \frac{\Delta n}{n} = -\frac{S\Delta xN\sigma}{S}, \\ \\ \frac{\Delta n}{n} = -N\sigma\Delta x. \end{array} [/math]

Znak minus wynika ze zmniejszanie się strumienia [math]\Delta n[/math] cząstek na drodze [math]\Delta x[/math]. Przechodząc od równania ze skończonymi przyrostami do równania różniczkowego:

[math] \frac{dn}{n} = -N\sigma x, [/math]

którego rozwiązaniem jest

[math] n(x) = n_0e^{-N\sigma x}. [/math]

, gdzie $n_0$ to początkowa liczba cząstek padajacych na tarczę.

Kształt zależności [math]n(x)[/math] umożliwia powiązanie przekroju czynnego na rozważany proces ze średnią drogą swobodną [math]\lambda[/math] na rozważany proces:

[math] \lambda = \langle x\rangle = \frac{\int^\infty_0 xe^{-N\sigma x}dx}{\int^\infty_0 e^{-N\sigma x}dx} = \frac{1}{N\sigma}, [/math]

wykładnik potęgowy w równaniu można zapisać w nieco zmodyfikowanej postaci:

[math] n(x) = n_0e^{-N\sigma x} = n_0e^{-\frac{x}{\lambda}} = n_0e^{-\mu x}=n_0e^{-\frac{\mu}{\rho}\rho x}. [/math]

Wielkość [math]\mu = \frac{1}{\lambda}[/math] nazywamy liniowym współczynnikiem osłabienia wiązki; [math]\frac{\mu}{\rho}[/math], gdzie [math]\rho[/math] oznacza gęstość ośrodka, nazywamy masowym współczynnikiem osłabienia wiązki. Wielkość [math]\rho x[/math] (wyrażana w [math]\frac{g}{cm^2}[/math] stanowi miarę grubości warstwy ośrodka, uwzględniając zarazem jego gęstość. Jednostką przekroju czynnego używaną w fizyce jest barn (1b = [math]10^{-28} m^2[/math]).

Rozpraszanie sprężyste (Rayleigh’a i Thompsona)

Jest to rozpraszanie elastyczne, w którym fala padająca nie zmienia swojej częstości (energii). W podejściu klasycznym (model atomu Lorentz’a) zmienne pole elektryczne fali padającej na atom wzbudza drgania elektronu. Elektron wykonując ruch drgający (a zatem przyspieszony), emituje promieniowanie. Rozkład kątowy tego promieniowania jest jednorodny.

Rozpraszanie Rayleigha

Rozpraszanie Rayleigha zachodzi na elektronach związanych w atomie. Przekrój czynny na ten rodzaj oddziaływania wynosi:

[math] \sigma_{\text{R}} = \frac{8}{3}\pi\left(\frac{e^2}{m_ec^2}\right)^2\frac{\omega^4}{\left(\omega_0^2-\omega^2\right)^2}. [/math]

Rozpraszanie Thomsona

Rozpraszanie Thompsona jest rozpraszaniem fali elektromagnetycznej na swobodnych elektronach [math]\omega_{0}=0[/math], wtedy przekrój czynny:

[math] \sigma_{\text{T}} = \frac{8}{3}\pi r_0^2 , [/math]

gdzie: [math] r_0 = \frac{e^2}{m_ec^2}[/math] i nie zależy od częstości fali padającej.

Rozpraszanie niesprężyste

Efekt fotoelektryczny, Rozpraszanie Comptona oraz proces Kreacji Par są rodzajem oddziaływania promieniowania elektromagnetycznego z materią, która prowadzi do zmiany długości fali.

Efekt Fotoelektryczny.

Efekt fotoelektryczny.

Zjawisko fotoelektryczne jest to pochłonięcie fotonu przez atom i emisja elektronu z powłoki leżącej w pobliżu jądra. Zjawisko fotoelektryczne:

• prowadzi do jonizacji atomu,
• może zachodzić wyłącznie dla elektronów związanych w atomach.

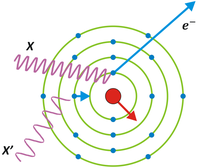
Po wybiciu elektronu z powłoki bliższej jądra, może nastąpić przeskok na tę powłokę elektronu z powłoki dalszej, połączony z emisją kwantu promieniowania elektromagnetycznego (na rysunku rys. 2) foton ten oznaczono przy pomocy symbolu X' . Czasami jednak wyzwalana energia nie jest zamieniana na promieniowanie lecz przekazywana innemu elektronowi powodując jego uwolnienie z atomu. Taki elektron określa się jako elektron Auger’a. Przekrój czynny na efekt fotoelektryczny wynosi:

[math] \sigma_{\text{EF}} = C\frac{Z^k}{E_\gamma^n}, [/math]

gdzie: [math]k[/math] = 4.0 i [math]n[/math] = 3.5 dla energii niskich [math](E_{\gamma}\ll m_0c^2)[/math] i [math]k = 4.6[/math] i [math]n = 1[/math] dla energii bardzo wysokich ([math]E_{\gamma}\gg m_0c^2[/math]).

Rozpraszanie Comptona

Efekt Comptona.

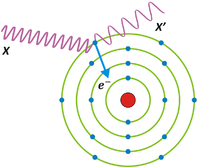
Zjawisko Comptona jest to rozpraszanie fotonów o wysokiej energii na swobodnych lub słabo związanych elektronach. Po rozproszeniu foton zmienia swoją energię, a zatem i związanej z nim długość fali:

[math] \lambda'-\lambda = \frac{h}{m_e c}\left(1-\cos\Theta\right). [/math]

Przekrój czynny na efekt Comptona wyraża wzór Kleina-Nishiny. Z uwago na jego złożoną formę, nie będzie podawany w poniższych materiałach. Warto jednak zapamiętać, iż przekrój czynny na efekt Comptona maleje wraz ze wzrostem energii fotonu. Zjawisko Comptona zachodzi na słabo związanych lub swobodnych elektronach. W porównaniu ze zjawiskiem fotoelektrycznym, energia padającego fotonu ulega częściowej absorpcji, zaś sam foton ulega rozproszeniu. W Efekcie Comptona można zatem wyróżnić dwa przekroje czynne - ze względu na absorpcję promieniowania jak i jego rozproszenie. Zjawisko rozpraszania fotonów jest bardzo istotne z punktu widzenia obrazowanie rentgenowskiego (jest jednym z główny czynników pogarszających rozdzielczość obrazu).

Kreacja Par

Kreacja Par.

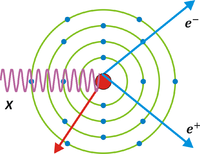
Kreacja par elektron-pozyton polega na zamianie fotonu w parę: pozyton i elektron. Jest to możliwe jedynie, gdy energia fotonu przekracza pewną określoną wartość zwaną energią progową [math](2\cdot m_e = 1.022)[/math], co wynika z warunku spełnienia w tym procesie praw zachowania energii i pędu. Równoczesne spełnienie obu praw zachowania wymaga, by proces ten zachodził z udziałem "trzeciego ciała", jakim może być jądro atomowe lub elektron, nie może natomiast zachodzić w próżni. Przekaz energii i pędu zachodzi za pośrednictwem pola elektrostatycznego (kulombowskiego) jądra lub elektronu. W wyniku zajścia zjawiska foton zostaje usunięty z padającej wiązki. Mamy zatem do czynienia ze zjawiskiem absorpcji, którego przekrój czynny wynosi:

[math] \sigma_{\text{K}} = \left(\frac{e^2}{mc^2}\right)^2\alpha Z^2f(E_{\gamma})[/math],

gdzie [math]\alpha=\frac{1}{137} [/math].