Obrazowanie:Obrazowanie Medyczne/Metody obrazowania medycznego wykorzystujące promieniowanie rentgenowskie: Różnice pomiędzy wersjami
| Linia 47: | Linia 47: | ||
====Maksymalna energia promieniowania X. Granica krótkofalowa promieniowania rentgenowskiego==== | ====Maksymalna energia promieniowania X. Granica krótkofalowa promieniowania rentgenowskiego==== | ||
Zgodnie z zasadą zachowania energii, cząstka nie może wypromieniować więcej energii niż wynosi jej energia kinetyczna. Jeśli napięcie przyspieszające elektron wynosi ''U'', cząstka zyska energię kinetyczną: | Zgodnie z zasadą zachowania energii, cząstka nie może wypromieniować więcej energii niż wynosi jej energia kinetyczna. Jeśli napięcie przyspieszające elektron wynosi ''U'', cząstka zyska energię kinetyczną: | ||
| − | <equation> | + | <equation id="2"> |
<math>E_k = U\cdot e</math> | <math>E_k = U\cdot e</math> | ||
</equation> | </equation> | ||
gdzie: ''e'' — ładunek elektronu. <br> | gdzie: ''e'' — ładunek elektronu. <br> | ||
Maksymalna energię ''E'' jaką może uzyskać foton Rentgenowski jest zatem równa: | Maksymalna energię ''E'' jaką może uzyskać foton Rentgenowski jest zatem równa: | ||
| − | <equation> | + | <equation id="3"> |
<math>E = E_k</math> | <math>E = E_k</math> | ||
</equation> | </equation> | ||
| Linia 58: | Linia 58: | ||
Maksymalna częstość promieniowania rentgenowskiego wynosi zatem: | Maksymalna częstość promieniowania rentgenowskiego wynosi zatem: | ||
| − | <equation> | + | <equation id="4"> |
<math>E = h\nu\rightarrow \nu= \frac{eU}{h}</math> | <math>E = h\nu\rightarrow \nu= \frac{eU}{h}</math> | ||
</equation> | </equation> | ||
zaś jego długość: | zaś jego długość: | ||
| − | <equation> | + | <equation id="5"> |
<math>\lambda_g = \frac{hc}{Ue}</math> | <math>\lambda_g = \frac{hc}{Ue}</math> | ||
</equation> | </equation> | ||
| Linia 73: | Linia 73: | ||
Wiemy już, iż promieniowanie X wytwarzane w lampie rentgenowskiej osiąga pewną maksymalną energię (albo odpowiadającej jej pewną minimalną długość fali). Nie znamy jednak jeszcze całościowego mechanizmu powstawania widma ciągłego. Niestety, mechanizm ten jest bardzo skomplikowany i wykracza znacznie poza ramy niniejszego podręcznika. W tym miejscu zaprezentujemy jedynie pewien model generacji widma w lampie rentgenowskiej zaproponowany przez Kramera w roku 1923. Jest to model stosunkowo prosty, ale posiadający pewne wady i krytykowany, jednakże model ten umożliwia wyjaśnienie powstawania rozkładu natężenie promieniowania X. <br> | Wiemy już, iż promieniowanie X wytwarzane w lampie rentgenowskiej osiąga pewną maksymalną energię (albo odpowiadającej jej pewną minimalną długość fali). Nie znamy jednak jeszcze całościowego mechanizmu powstawania widma ciągłego. Niestety, mechanizm ten jest bardzo skomplikowany i wykracza znacznie poza ramy niniejszego podręcznika. W tym miejscu zaprezentujemy jedynie pewien model generacji widma w lampie rentgenowskiej zaproponowany przez Kramera w roku 1923. Jest to model stosunkowo prosty, ale posiadający pewne wady i krytykowany, jednakże model ten umożliwia wyjaśnienie powstawania rozkładu natężenie promieniowania X. <br> | ||
Model Kramera opisuje emisję promieniowania Rentgenowskiego w wyniku oddziaływania z bardzo cienką tarczą. Przewiduje on widmo emitowanego promieniowanie w postaci: | Model Kramera opisuje emisję promieniowania Rentgenowskiego w wyniku oddziaływania z bardzo cienką tarczą. Przewiduje on widmo emitowanego promieniowanie w postaci: | ||
| − | <equation> | + | <equation id="6"> |
<math>I(\nu)d\nu = | <math>I(\nu)d\nu = | ||
\left\{ | \left\{ | ||
| Linia 89: | Linia 89: | ||
Aby uzyskać widmo promieniowania rentgenowskiego w funkcji długości fali, należy wykonać następujące przekształcenia. Wiemy, że widmo emitowane w wyniku oddziaływania elektronów z cienką tarczą ma postać: | Aby uzyskać widmo promieniowania rentgenowskiego w funkcji długości fali, należy wykonać następujące przekształcenia. Wiemy, że widmo emitowane w wyniku oddziaływania elektronów z cienką tarczą ma postać: | ||
| − | <equation> | + | <equation id="7"> |
<math> I(\nu) = \left\{ | <math> I(\nu) = \left\{ | ||
\begin{array}{lll} | \begin{array}{lll} | ||
| Linia 100: | Linia 100: | ||
</equation> | </equation> | ||
Zależność pomiędzy częstością fali a jej długością opisuje następujący wzór: | Zależność pomiędzy częstością fali a jej długością opisuje następujący wzór: | ||
| − | <equation> | + | <equation id="8"> |
<math> \lambda = \frac{c}{\nu}</math> | <math> \lambda = \frac{c}{\nu}</math> | ||
</equation> | </equation> | ||
gdzie ''c'' — prędkość światła. | gdzie ''c'' — prędkość światła. | ||
Obliczając przyrost długości fali w funkcji przyrostu częstości fali otrzymujemy: | Obliczając przyrost długości fali w funkcji przyrostu częstości fali otrzymujemy: | ||
| − | <equation> | + | <equation id="9"> |
<math> d\lambda = -\frac{c}{\nu^2}d\nu</math> | <math> d\lambda = -\frac{c}{\nu^2}d\nu</math> | ||
</equation> | </equation> | ||
z kolei związek pomiędzy natężeniem promieniowania elektromagnetycznego wyemitowane w wąskim przedziale częstości <math>d\nu</math> oraz wąskim przedziale długości fal: | z kolei związek pomiędzy natężeniem promieniowania elektromagnetycznego wyemitowane w wąskim przedziale częstości <math>d\nu</math> oraz wąskim przedziale długości fal: | ||
| − | <equation> | + | <equation id="10"> |
<math> I(\lambda)d\lambda = -I(\nu)d\nu\rightarrow I(\lambda)\frac{d\nu}{d\lambda} | <math> I(\lambda)d\lambda = -I(\nu)d\nu\rightarrow I(\lambda)\frac{d\nu}{d\lambda} | ||
</math> | </math> | ||
</equation> | </equation> | ||
Ponieważ <math> \frac{d\lambda}{d\nu} = -\frac{c}{\nu^2}</math>, ostatecznie dostajemy: | Ponieważ <math> \frac{d\lambda}{d\nu} = -\frac{c}{\nu^2}</math>, ostatecznie dostajemy: | ||
| − | <equation> | + | <equation id="11"> |
<math> I(\lambda) = \left\{ | <math> I(\lambda) = \left\{ | ||
\begin{array}{lll} | \begin{array}{lll} | ||
| Linia 141: | Linia 141: | ||
Trzeci spośród procesów jest tematem niniejszego rozdziału. Po wybiciu elektronu, powłoka może zostać zapełniona przez elektrod z powłoki o wyższej energii. W trakcie tego procesu, elektron emituje nadwyżkę swojej energii w postaci promieniowania elektromagnetycznego. Różnica poziomów energetycznych w atomie, a w związku z tym i energia promieniowania elektromagnetycznego wynosi: | Trzeci spośród procesów jest tematem niniejszego rozdziału. Po wybiciu elektronu, powłoka może zostać zapełniona przez elektrod z powłoki o wyższej energii. W trakcie tego procesu, elektron emituje nadwyżkę swojej energii w postaci promieniowania elektromagnetycznego. Różnica poziomów energetycznych w atomie, a w związku z tym i energia promieniowania elektromagnetycznego wynosi: | ||
| − | <equation> | + | <equation id="2"> |
<math>\Delta E \approx C\left[\frac{1}{m^2} - \frac{1}{n^2}\right]</math> | <math>\Delta E \approx C\left[\frac{1}{m^2} - \frac{1}{n^2}\right]</math> | ||
</equation> | </equation> | ||
| Linia 164: | Linia 164: | ||
W zakresie energii stosowanych w Obrazowaniu Medycznym promieniowanie Rentgenowskie oddziałuje z materia w procesach rozproszenia Rayleigh’a, Thomsona i Comptona oraz efekcie fotoelektrycznym. Każdy z tych procesów scharakteryzowany jest przez przekrój czynny σ. Przypominamy, wzór na osłabienie wiązki promieniowania w funkcji przebytej drogi: | W zakresie energii stosowanych w Obrazowaniu Medycznym promieniowanie Rentgenowskie oddziałuje z materia w procesach rozproszenia Rayleigh’a, Thomsona i Comptona oraz efekcie fotoelektrycznym. Każdy z tych procesów scharakteryzowany jest przez przekrój czynny σ. Przypominamy, wzór na osłabienie wiązki promieniowania w funkcji przebytej drogi: | ||
| − | <equation> | + | <equation id="13"> |
<math> n(x) = n_0e^{-N\sigma x} </math>, | <math> n(x) = n_0e^{-N\sigma x} </math>, | ||
</equation> | </equation> | ||
| Linia 170: | Linia 170: | ||
<math>N</math> — ilość centrów oddziaływania na jednostkę objętości. <br> | <math>N</math> — ilość centrów oddziaływania na jednostkę objętości. <br> | ||
Wprowadzone zostało również pojecie średniej drogi swobodnej: | Wprowadzone zostało również pojecie średniej drogi swobodnej: | ||
| − | <equation> | + | <equation id="14"> |
<math>\lambda = \langle x \rangle = \frac{1}{N\sigma}</math> | <math>\lambda = \langle x \rangle = \frac{1}{N\sigma}</math> | ||
</equation> | </equation> | ||
oraz liniowy współczynnik osłabienia wiązki promieniowania: | oraz liniowy współczynnik osłabienia wiązki promieniowania: | ||
| − | <equation> | + | <equation id="15"> |
<math>\mu = N\sigma.</math> | <math>\mu = N\sigma.</math> | ||
</equation> | </equation> | ||
| Linia 185: | Linia 185: | ||
<math>I</math> — natężenie wiązki po pokonaniu w ośrodku drogi ''x''. | <math>I</math> — natężenie wiązki po pokonaniu w ośrodku drogi ''x''. | ||
Jeżeli promieniowanie Rentgenowskie przechodzi przez ośrodki o różnym współczynniku μ (patrz <xr id="fig:mu_niejednorodne">rys. %i</xr>), wtedy wzór ( <xr id="eq:lambert_beer"> %i</xr>) przekształca się do postaci: | Jeżeli promieniowanie Rentgenowskie przechodzi przez ośrodki o różnym współczynniku μ (patrz <xr id="fig:mu_niejednorodne">rys. %i</xr>), wtedy wzór ( <xr id="eq:lambert_beer"> %i</xr>) przekształca się do postaci: | ||
| − | <equation> | + | <equation id="15"> |
<math> | <math> | ||
\begin{array}{l} | \begin{array}{l} | ||
| Linia 204: | Linia 204: | ||
<math>I_i</math> — natężenie promieniowania rentgenowskiego po przebyciu drogi ''x'' w ''i''-tym ośrodku, charakteryzującym się liniowym współczynnikiem osłabienia promieniowania rentgenowskiego <math>\mu_i</math>. Zanim promieniowanie rentgenowskie dotrze do ''i''-tego ośrodka, przechodzi przez ośrodki o współczynniku osłabienia <math>\mu_1, \mu_2, \ldots, \mu_{i-1}</math>. Przechodząc od struktur dyskretnych do ciągłych dostajemy: | <math>I_i</math> — natężenie promieniowania rentgenowskiego po przebyciu drogi ''x'' w ''i''-tym ośrodku, charakteryzującym się liniowym współczynnikiem osłabienia promieniowania rentgenowskiego <math>\mu_i</math>. Zanim promieniowanie rentgenowskie dotrze do ''i''-tego ośrodka, przechodzi przez ośrodki o współczynniku osłabienia <math>\mu_1, \mu_2, \ldots, \mu_{i-1}</math>. Przechodząc od struktur dyskretnych do ciągłych dostajemy: | ||
| − | <equation><math> | + | <equation id="16"><math> |
I\left(x\right) = I_0 e^{\int_{x=0}^{x=d} -\mu(x) dx}. | I\left(x\right) = I_0 e^{\int_{x=0}^{x=d} -\mu(x) dx}. | ||
</math></equation> | </math></equation> | ||
| Linia 229: | Linia 229: | ||
Interesuje nas na razie tylko, jaki teoretycznie możemy uzyskać kontrast na zdjęciu wykonanym przy pomocy promieniowania Rentgenowskiego. | Interesuje nas na razie tylko, jaki teoretycznie możemy uzyskać kontrast na zdjęciu wykonanym przy pomocy promieniowania Rentgenowskiego. | ||
W tym celu załóżmy, iż wiązka promieniowania rentgenowskiego przechodzi przez ośrodek o grubości ''L'' i liniowym współczynniku promieniowania X równym <math>\mu_1</math>. W ośrodku znajduje się struktura o grubości ''d'' i liniowym współczynniku osłabienia promieniowa X równym <math>\mu_2</math> (patrz <xr id="fig:struktura">rys. %i</xr>). Wyznaczmy na początku kontrast lokalny: | W tym celu załóżmy, iż wiązka promieniowania rentgenowskiego przechodzi przez ośrodek o grubości ''L'' i liniowym współczynniku promieniowania X równym <math>\mu_1</math>. W ośrodku znajduje się struktura o grubości ''d'' i liniowym współczynniku osłabienia promieniowa X równym <math>\mu_2</math> (patrz <xr id="fig:struktura">rys. %i</xr>). Wyznaczmy na początku kontrast lokalny: | ||
| − | <equation><math>C = \frac{I_2 - I_1}{I_1} </math></equation> | + | <equation id="17"><math>C = \frac{I_2 - I_1}{I_1} </math></equation> |
gdzie:<br> | gdzie:<br> | ||
<math>I_1</math> — natężenie promieniowania po przejściu tylko przez ośrodek o współczynniku liniowego osłabienia promieniowania X równym <math>\mu_1</math>. <br> | <math>I_1</math> — natężenie promieniowania po przejściu tylko przez ośrodek o współczynniku liniowego osłabienia promieniowania X równym <math>\mu_1</math>. <br> | ||
<math>I_2</math> — natężenie promieniowania po przejściu przez ośrodki o współczynniku liniowego osłabienia promieniowania X równym <math>\mu_1</math> i <math>\mu_1</math>. <br> | <math>I_2</math> — natężenie promieniowania po przejściu przez ośrodki o współczynniku liniowego osłabienia promieniowania X równym <math>\mu_1</math> i <math>\mu_1</math>. <br> | ||
Po wykonaniu prostych obliczeń otrzymujemy: | Po wykonaniu prostych obliczeń otrzymujemy: | ||
| − | <equation> | + | <equation id="8"> |
<math>\begin{array}{l} | <math>\begin{array}{l} | ||
I_1 = I_0e^{-\mu_1L} \\ | I_1 = I_0e^{-\mu_1L} \\ | ||
| Linia 247: | Linia 247: | ||
Załóżmy teraz dla uproszczenia, że nasza struktura ma niewielkie rozmiary oraz różnica w liniowym współczynniku osłabienia promieniowanie X <math>\Delta\mu</math> jest również niewielki, czyli gdy | Załóżmy teraz dla uproszczenia, że nasza struktura ma niewielkie rozmiary oraz różnica w liniowym współczynniku osłabienia promieniowanie X <math>\Delta\mu</math> jest również niewielki, czyli gdy | ||
| − | <equation> | + | <equation id="19"> |
<math> | <math> | ||
\Delta\mu d \ll 1 | \Delta\mu d \ll 1 | ||
| Linia 253: | Linia 253: | ||
</equation> | </equation> | ||
wtedy: | wtedy: | ||
| − | <equation> | + | <equation id="20"> |
<math> | <math> | ||
I_2 - I_1 = -\Delta\mu dI_0e^{-\mu_1L} | I_2 - I_1 = -\Delta\mu dI_0e^{-\mu_1L} | ||
| Linia 259: | Linia 259: | ||
</equation> | </equation> | ||
zaś kontrast lokalny wynosi: | zaś kontrast lokalny wynosi: | ||
| − | <equation> | + | <equation id="21"> |
<math> | <math> | ||
C = \frac{I_2 - I_1}{I_2} = \frac{-\Delta\mu d I_0e^{-\mu_1L}}{I_0 e^{-\mu_1L}} = -\Delta\mu d | C = \frac{I_2 - I_1}{I_2} = \frac{-\Delta\mu d I_0e^{-\mu_1L}}{I_0 e^{-\mu_1L}} = -\Delta\mu d | ||
| Linia 317: | Linia 317: | ||
Jednym z najważniejszych parametrów charakteryzujących filmy wykorzystywane w klasycznej diagnostyce rentgenowskiej jest tzw. gęstość optyczna. Zrozumienie tego parametru oraz jego zależność od ekspozycji umożliwi również zrozumienie przyczyn intensywnych badań nad detektorami cyfrowymi, które wypierają filmy z zastosowań w diagnostyce medycznej. | Jednym z najważniejszych parametrów charakteryzujących filmy wykorzystywane w klasycznej diagnostyce rentgenowskiej jest tzw. gęstość optyczna. Zrozumienie tego parametru oraz jego zależność od ekspozycji umożliwi również zrozumienie przyczyn intensywnych badań nad detektorami cyfrowymi, które wypierają filmy z zastosowań w diagnostyce medycznej. | ||
Zdefiniujmy na początku stopień zaczernienia filmu w wyniku ekspozycji. W tym celu możemy zmierzyć transmisję promieniowania przechodzące przez kliszę. Stopień zaczernienia filmu jest natężenia promieniowania przechodzącego przez klisze <math>I</math> do natężenia padającego na kliszę <math>I_0</math>: | Zdefiniujmy na początku stopień zaczernienia filmu w wyniku ekspozycji. W tym celu możemy zmierzyć transmisję promieniowania przechodzące przez kliszę. Stopień zaczernienia filmu jest natężenia promieniowania przechodzącego przez klisze <math>I</math> do natężenia padającego na kliszę <math>I_0</math>: | ||
| − | <equation> | + | <equation id="22"> |
<math> T = \frac{I}{I_0}</math>. | <math> T = \frac{I}{I_0}</math>. | ||
</equation> | </equation> | ||
Gęstość optyczna to: | Gęstość optyczna to: | ||
| − | <equation> | + | <equation id="23"> |
<math> D =-log_{10}(T) = log_{10}\frac{I_0}{I} </math>. | <math> D =-log_{10}(T) = log_{10}\frac{I_0}{I} </math>. | ||
</equation> | </equation> | ||
| Linia 361: | Linia 361: | ||
*Kontrast — Zakres ekspozycji w którym gęstość optyczna zmienia się liniowo. Filmy o szeroki zakresie użytecznej ekspozycji są tzw. filmami o małej dynamice kontrastu. Z kolei filmy o wąskim zakresie użytecznej ekspozycji to filmy o tzw. dużej dynamice kontrastu, które jednakże łatwo prześwietlić lub nie doświetlić. | *Kontrast — Zakres ekspozycji w którym gęstość optyczna zmienia się liniowo. Filmy o szeroki zakresie użytecznej ekspozycji są tzw. filmami o małej dynamice kontrastu. Z kolei filmy o wąskim zakresie użytecznej ekspozycji to filmy o tzw. dużej dynamice kontrastu, które jednakże łatwo prześwietlić lub nie doświetlić. | ||
* Średni kontrast (ang ''Average Contrast''): | * Średni kontrast (ang ''Average Contrast''): | ||
| − | <equation> | + | <equation id="24"> |
<math>C = \frac{D(E_2)-D(E_1)}{E_2 - E_1} </math>. | <math>C = \frac{D(E_2)-D(E_1)}{E_2 - E_1} </math>. | ||
</equation> | </equation> | ||
* Gamma — kontrast maksymalny. | * Gamma — kontrast maksymalny. | ||
* Szybkość uzyskania gęstości optycznej D = 1: | * Szybkość uzyskania gęstości optycznej D = 1: | ||
| − | <equation> | + | <equation id="25"> |
<math>S = E^{-1}(D=1) </math>. | <math>S = E^{-1}(D=1) </math>. | ||
</equation> | </equation> | ||
| Linia 374: | Linia 374: | ||
* Technika Trzypunktowa — napięcie anodowe <math>U_A</math>, prąd anodowy <math>I_A</math> i czas wykonywania naświetlenia technik ustawia ręcznie. Przypominamy, że natężenie prądu anodowego <math>I_A</math> zależy zarówno on natężenia prądu płynącego przez katodę <math>I_K</math>jak i napięcie przyspieszającego <math>U_A</math>. Jednakże prąd <math>I_A</math> jest proporcjonalny do prądu <math>I_K</math> w związku z tym regulacja prądu anodowego odbywa się głównie poprzez zmiany prądu płynącego przez katodę. | * Technika Trzypunktowa — napięcie anodowe <math>U_A</math>, prąd anodowy <math>I_A</math> i czas wykonywania naświetlenia technik ustawia ręcznie. Przypominamy, że natężenie prądu anodowego <math>I_A</math> zależy zarówno on natężenia prądu płynącego przez katodę <math>I_K</math>jak i napięcie przyspieszającego <math>U_A</math>. Jednakże prąd <math>I_A</math> jest proporcjonalny do prądu <math>I_K</math> w związku z tym regulacja prądu anodowego odbywa się głównie poprzez zmiany prądu płynącego przez katodę. | ||
* technika dwupunktowa — w przypadku tej techniki wprowadza się dodatkową wielkość — miliampero-sekundy (mAs): | * technika dwupunktowa — w przypadku tej techniki wprowadza się dodatkową wielkość — miliampero-sekundy (mAs): | ||
| − | <equation> | + | <equation id="26"> |
<math> | <math> | ||
\text{mAs} = I_A\cdot t [A\cdot s] | \text{mAs} = I_A\cdot t [A\cdot s] | ||
Aktualna wersja na dzień 20:45, 31 paź 2015
Metody obrazowania medycznego wykorzystujące promieniowanie rentgenowskie
Obecnie metody diagnostyki medycznej, wykorzystujące promieniowanie rentgenowskie, można podzielić ogólnie na dwie grupy:
- Rentgenografię Klasyczną (inne często spotykane określenia, to Radiografia, RTG konwencjonalne, RTG planarne, (ang. planar radiography)).
- Rentgenowską Tomografię Komputerową (ang. X-Ray Computer Tomography, CT).
Spis treści
- 1 Natura promieniowania Rentgenowskiego
- 2 Budowa i Zasada Działania Lampy Rentgenowskiej
- 3 długości fali zaprezentowano na rysunkuwania X uzyskiwane w lampie RTG
- 3.1 Mechanizm powstawania części ciągłej widma RTG
- 3.1.1 Maksymalna energia promieniowania X. Granica krótkofalowa promieniowania rentgenowskiego
- 3.1.2 Mechanizm powstawania widma ciągłego — model Kramera (1923).
- 3.1.3 Naturalna filtracja promieniowania rentgenowskiego
- 3.1.4 Część dyskretna widma promieniowania X wytworzonego w lampie rentgenowskiej
- 3.2 Odprowadzanie ciepła w lampie rentgenowskiej
- 3.1 Mechanizm powstawania części ciągłej widma RTG
- 4 Osłabienie promieniowania X przez materię
- 5 Natężenie promieniowania Rentgenowskiego emitowanego przez Lampę Rentgenowską
- 6 Kontrast obrazu uzyskanego przy pomocy promieniowania rentgenowskiego
- 7 Budowa Aparatury wykorzystywanej w Rentgenografii Klasycznej
- 8 Film i ekrany wzmacniające
- 9 System sterowania ekspozycją
- 10 Wzmacniacze Obrazu
- 11 Detektory Cyfrowe
Natura promieniowania Rentgenowskiego
Promieniowanie Rentgenowskie (nazywane również promieniowaniem X) jest promieniowaniem elektromagnetycznym powstałym w wyniku hamowania cząstek obdarzonych ładunkiem (stąd inna nazwa promieniowania Bremsstrahlung, niem. bremsen — hamować i Strahlung hamowanie). Wiadomo, że cząstki obdarzone ładunkiem elektrycznym, poruszające się ruchem przyspieszony emitują promieniowanie elektromagnetyczne, którego moc chwilową wyraża następujący wzór:
gdzie:
[math]t'=t - \frac{r}{c}[/math],
r — odległość od ładunku do punktu obserwacji,
c — prędkość światła,
a — przyspieszenie z jakim porusza się ładunek,
[math]\epsilon_0[/math] — przenikalność elektryczna próżni,
c — prędkość światła.
Długość fali promieniowania rentgenowskiego jest mniejsza od 3 nm co odpowiada energiom powyżej 400 eV. Wyróżnia się przy tym tzw. zakres promieniowania miękkiego — od 400 eV do 10 keV oraz promieniowania twardego, które charakteryzuje się energią powyżej 10 keV. Miękkie promieniowanie rentgenowskie jest absorbowane głównie przez powierzchniowe tkanki ciała ludzkiego i ma zbyt małą energię aby przez nie przeniknąć. W związku z tym nie znajduje zastosowania w Obrazowaniu Medycznym.
Uwaga — w wielu źródłach można spotkać się z definicją promieniowania rentgenowskiego jako promieniowania elektromagnetycznego o długości fali zawartej pomiędzy ultrafioletem a promieniowaniem gamma. Taka definicja nie jest jednak właściwa, bowiem obecnie można uzyskać promieniowanie rentgenowskie o energii odpowiadającej niskoenergetycznemu promieniowaniu gamma. Zasadniczą różnicą pomiędzy promieniowaniem gamma a promieniowaniem rentgenowskim jest sposób powstawania. Promieniowanie gamma jest promieniowaniem rentgenowskim powstałym w przemianach jądrowych, natomiast promieniowanie rentgenowskie jest promieniowaniem elektromagnetycznym emitowanym przez cząstkę poruszająca się ruchem przyspieszonym.
Promieniowania Rentgenowskiego stosowane w diagnostyce medycznej wytwarzane jest w tzw. Lampach Rentgenowskich.
Budowa i Zasada Działania Lampy Rentgenowskiej
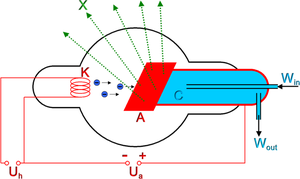
Schemat Lampy Rentgenowskiej zaprezentowano na rys. 1. Składa się ona z katody oraz anody, umieszczonych w szklanej bańce, z której usunięto powietrze. Do katody przyłożone jest napięcie, które wywołuje przepływ przez nią prądu rzędu ułamka ampera. Przepływ prądu powoduje rozgrzanie katody do temperatury około 2200 °C i w następstwie zjawisko termoemisji elektronów (czyli emisji elektronów przez podgrzany do wysokiej temperatury ciało Emisja termoelektronowa). Przy braku dodatkowego napięcia, elektrony emitowane przez katodę utworzyłyby wokół niej chmurę. Pomiędzy katodę a anodę przyłożone jest jednak napięcie [math]U_A[/math] (maksymalnie 150 kV), które powoduje ruch elektronów w kierunku anody. Elektrony zostają rozpędzone do prędkości około 0,1 prędkości światła po czym wnikają w anodę. W anodzie rozpędzone elektrony w wyniku szeregu różnych procesów, które zostaną omówione w kolejnych rozdziałach tracą swoją energię kinetyczną. Część tej energii zostaje przetworzona na promieniowanie elektromagnetyczne, jednak większość (ponad 95%) ulega przemianie w ciepło. W wyniku tego anoda rozgrzewa się do bardzo wysokich temperatur i musi być wykonana z materiałów o dużej wielkości atomowej [math]Z[/math] (aby skutecznie hamować elektrony) oraz wysokiej temperaturze topnienia. Materiałami, które wykorzystuje się do budowy lampy RTG to najczęściej miedź, wolfram lub molibden. Aby polepszyć chłodzenie lampy rentgenowskiej, do anody doprowadzone są przewody z wodą lub specjalnym olejem, który odprowadza od niej ciepło (na rys. 1 są to wejścia oznaczone jako [math]W_\mathrm{in}[/math] oraz [math]W_\mathrm{out}[/math]).
długości fali zaprezentowano na rysunkuwania X uzyskiwane w lampie RTG
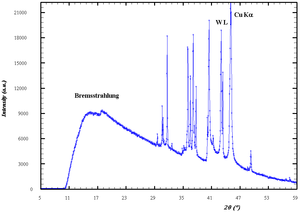
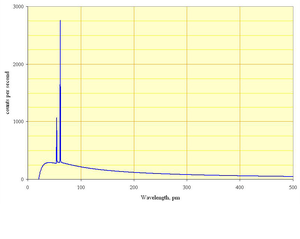
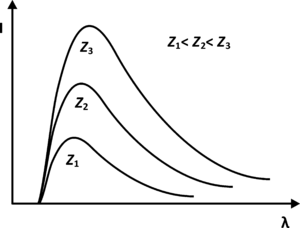
Natężenie promieniowania rentgenowskiego uzyskiwanego w lampie rentgenowskiej zaprezentowano na rys. 2 w funkcji energii tego promieniowania oraz na rys. 3 w funkcji długości fali. W widmach tych można wyróżnić trzy istotne cechy:
- Widmo promieniowania X zanika dla pewnej granicznej energii oraz długości fali.
- Istnienie części ciągłej widma.
- Istnienie części dyskretnej widma, nazywanej widmem charakterystycznym.
Omówimy teraz, w jaki sposób powstaje w lampie RTG promieniowanie o rozkładzie zaprezentowanym na rys. 2 i rys. 3.
Mechanizm powstawania części ciągłej widma RTG
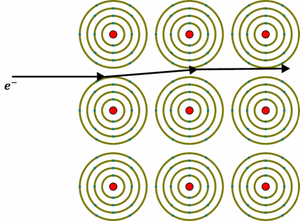
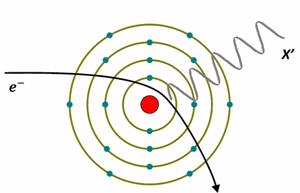
Jak wiemy, elektrony emitowane przez katodę zostają rozpędzone na drodze pomiędzy anodą a katodą. Wnikając w anodę, elektrony te będę przede wszystkim zderzać się z centrami sieci krystalicznej materiału, z którego wykonana jest anoda (rys. 4) . W wyniku wspomnianych zderzeń, energia kinetyczna elektronu przekazana sieci krystalicznej zostanie zamieniona na ciepło podgrzewające anodę. W ten sposób elektron traci ponad 95 % swojej energii kinetycznej, którą zyskał w trakcie przyspieszania na drodze pomiędzy katodą a anodą. Elektron może również nie ulec zderzeniu z siecią krystaliczną, lecz wniknąć wgłąb atomu. Pod wpływem oddziaływania Kulombowskiego z dodatnio naładowanym jądrem, tor ruchu elektronu zostaje zakrzywiony. Ruch po torze krzywoliniowym jest ruchem przyspieszonym, w wyniku którego elektron emituje promieniowanie elektromagnetyczne (patrz rys. 5. W takim przypadku elektron traci swoją energię kinetyczną, które ulega zamianie na energię promieniowania X. Pomimo, że mniej niż 2 % energii kinetycznej elektronów jest zamienianie w lampie rentgenowskiej na energię promieniowania elektromagnetycznego, wyhamowywanie elektronów jest najbardziej wydajnym sposobem uzyskiwania promieniowania X. Natężenie emitowanego promieniowania silnie bowiem spada wraz z masą przyspieszanej cząstki, a kolejna obdarzona ładunkiem cząstka jest już 200 razy cięższa od elektronu.
Maksymalna energia promieniowania X. Granica krótkofalowa promieniowania rentgenowskiego
Zgodnie z zasadą zachowania energii, cząstka nie może wypromieniować więcej energii niż wynosi jej energia kinetyczna. Jeśli napięcie przyspieszające elektron wynosi U, cząstka zyska energię kinetyczną:
gdzie: e — ładunek elektronu.
Maksymalna energię E jaką może uzyskać foton Rentgenowski jest zatem równa:
Na rys. 2 widzimy, że widmo promieniowania X zanika dla energii 100 keV. Możemy na tej podstawie wywnioskować, że napięcie przyspieszające elektrony wynosiła 100 kV.
Maksymalna częstość promieniowania rentgenowskiego wynosi zatem:
zaś jego długość:
Wielkość [math]\lambda_g[/math] nazywamy granicą krótkofalową promieniowania X emitowanego z lampy rentgenowskiej.
Mechanizm powstawania widma ciągłego — model Kramera (1923).
Wiemy już, iż promieniowanie X wytwarzane w lampie rentgenowskiej osiąga pewną maksymalną energię (albo odpowiadającej jej pewną minimalną długość fali). Nie znamy jednak jeszcze całościowego mechanizmu powstawania widma ciągłego. Niestety, mechanizm ten jest bardzo skomplikowany i wykracza znacznie poza ramy niniejszego podręcznika. W tym miejscu zaprezentujemy jedynie pewien model generacji widma w lampie rentgenowskiej zaproponowany przez Kramera w roku 1923. Jest to model stosunkowo prosty, ale posiadający pewne wady i krytykowany, jednakże model ten umożliwia wyjaśnienie powstawania rozkładu natężenie promieniowania X.
Model Kramera opisuje emisję promieniowania Rentgenowskiego w wyniku oddziaływania z bardzo cienką tarczą. Przewiduje on widmo emitowanego promieniowanie w postaci:
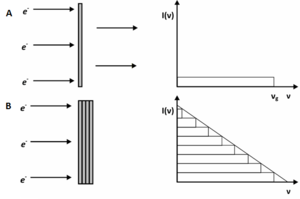
Jak można zauważyć, model przewiduje jednorodny rozkład energii promieniowania rentgenowskiego emitowanego przez cienka tarczę. Widmo to kończy się na częstości [math]\nu_g[/math]. Częstości tej odpowiada maksymalna energia jaką elektrony mogą zamienić na energię promieniowania elektromagnetycznego (patrz rys. 6.A).
Korzystając z modelu Kramera możemy również oszacować postać widma promieniowania rentgenowskiego emitowanego z grubej tarczy (np. anody lampy RTG). Tarcza taka będzie się składać z wielu cienkich tarcz. Widmo emitowane z każdej cienkiej zaprezentowano na rys. 6.A, przy czym przy każdej cienkiej tarczy odpowiada inna wartości częstości granicznej [math]\nu_g[/math], dla której widmo promieniowania rentgenowskiego zanika. Spowodowane jest to faktem, iż w każdej kolejnej tarczy elektrony część swojej energii kinetycznej zamieniają na promieniowanie rentgenowskie. Załóżmy, że w pierwszą cienką warstwę wnika N elektronów o energii kinetyczną E, z których n elektronów całą swoją energię kinetyczną zamieni na promieniowanie rentgenowskie. W związku z tym elektrony te nie będą w stanie wniknąć do kolejnej cienkiej tarczy. Pozostałe elektrony z wiązki zamieniły na promieniowanie elektromagnetyczne tylko część swojej energii, którą oznaczymy [math]\Delta E[/math]. Po opuszczeniu pierwszej cienkiej tarczy, wiązka zawiera N-n elektronów o maksymalnych energiach [math]E-\Delta E[/math]. Wnikając do kolejnej cienkiej tarczy, elektrony mogą zatem oddać co najwyżej energię [math]E-\Delta E[/math], której odpowiada częstość graniczna [math]\nu_g = \frac{E-\Delta E}{h}[/math], która jest niższa niż częstość graniczna uzyskana w widmie pochodzącym z pierwszej cienkiej tarczy: [math]\nu_g = \frac{E}{h}[/math]. Sumując widma pochodzące od wielu cienkich tarcz uzyskujemy zanikające liniowo widmo promieniowania X.
Aby uzyskać widmo promieniowania rentgenowskiego w funkcji długości fali, należy wykonać następujące przekształcenia. Wiemy, że widmo emitowane w wyniku oddziaływania elektronów z cienką tarczą ma postać:
Zależność pomiędzy częstością fali a jej długością opisuje następujący wzór:
gdzie c — prędkość światła. Obliczając przyrost długości fali w funkcji przyrostu częstości fali otrzymujemy:
z kolei związek pomiędzy natężeniem promieniowania elektromagnetycznego wyemitowane w wąskim przedziale częstości [math]d\nu[/math] oraz wąskim przedziale długości fal:
Ponieważ [math] \frac{d\lambda}{d\nu} = -\frac{c}{\nu^2}[/math], ostatecznie dostajemy:
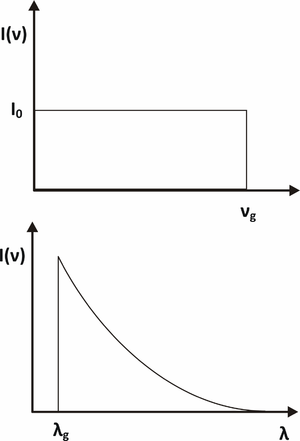
Widmo promieniowanie X, emitowanego w lampie rentgenowskiej, w funkcji częstości i długości fali zaprezentowano na rysunku rys. 7.
Naturalna filtracja promieniowania rentgenowskiego
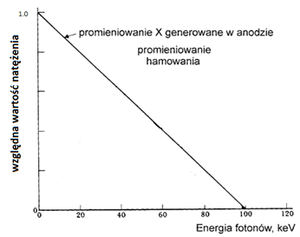
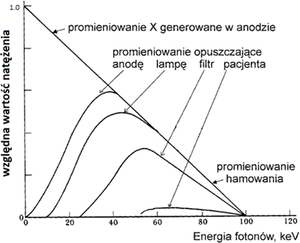
Na rys. 8 zaprezentowano teoretyczny kształt widma, jaki powstaje w wyniku hamowania elektronów w tarczy lampy rentgenowskiej. W praktyce jednak, widmo to odbiega od kształtu przewidzianego przez model Kramera. Promieniowanie X, zanim opuści anodę, oddziałuje z jej atomami w procesach: fotoelektrycznym i comptonowskim. Na skutek wymienionych procesów, ulega zmniejszeniu natężenie promieniowania rentgenowskiego. Ponadto, w celu przeciwdziałania propagacji promieniowania X we wszystkich kierunkach, lampa rentgenowska znajduje się w ołowianej koszulce (tzw. kołpaku), o grubości kilku milimetrów. Promieniowania z lampy rentgenowskie wydostaje się na zewnątrz poprzez okienko wykonane z berylu. Beryl, mimo że dobrze transmituje promieniowanie rentgenowskie, również osłabia do pewnego stopnia natężenie promieniowania X. Zmniejszanie natężenia promieniowania X po przejściu przez kolejne ośrodki zaprezentowano na rysunku rys. 9. Jak można zauważyć, z wiązki promieniowania X usuwane są w szczególności fotony niskoenergetyczne.
Część dyskretna widma promieniowania X wytworzonego w lampie rentgenowskiej
Przypominamy, że elektron wnikający w anodę, traci swoją energię kinetyczną w wyniku trzech procesów:
- zderzeń z siecią krystaliczną anody,
- emisji promieniowania hamowania,
- wybijania elektronów z powłok atomowych.
Trzeci spośród procesów jest tematem niniejszego rozdziału. Po wybiciu elektronu, powłoka może zostać zapełniona przez elektrod z powłoki o wyższej energii. W trakcie tego procesu, elektron emituje nadwyżkę swojej energii w postaci promieniowania elektromagnetycznego. Różnica poziomów energetycznych w atomie, a w związku z tym i energia promieniowania elektromagnetycznego wynosi:
gdzie:
[math]m, n[/math] — główne liczby kwantowe powłok,
[math]C[/math] — stała zależna od liczby atomowej Z (ładunku jądra), stałej Rydberga oraz stałej ekranowania.
Przykładowo, dla miedzi, stała [math]C\approx 10[/math] keV. Jeśli elektron wnikający w anodę wybiję elektron z niskiej powłoki i jednocześnie luka po wybitym elektronie zostanie zastąpiona przez elektron z powłoki o wysokiej głównej liczbie kwantowej, wtedy emitowany kwant promieniowania elektromagnetycznego może mieć energię odpowiadającą fotonowi rentgenowskiemu.
W trakcie zmiany przez elektron orbity może być emitowane promieniowanie elektromagnetyczne o ściśle określonych energiach, w związku z czym proces wybijania elektronów z atomów anody prowadzi do powstawania widma składającego się z dyskretnych linii. Widmo to nazywane jest widmem charakterystycznym, gdyż układ linii spektralnych jest charakterystyczny dla danego pierwiastka. Promieniowanie charakterystyczne dla napięcia poniżej 60 kV praktycznie jest pomijalne (ale wykorzystuje się je w mammografii). Dla napięcia anodowego wynoszącego 130 kV wkład widma charakterystycznego w rozkładzie energii promieniowania X wynosi około 5%.
Widmo ciągłe i charakterystyczne promieniowania powstałego w lampie rentgenowskiej nakładają się na siebie. Kształt widma wypadkowego zaprezentowano na rys. 2.
Odprowadzanie ciepła w lampie rentgenowskiej
Miejsce na anodzie, które jest bombardowane przez elektrony nazywamy ogniskiem. Rozmiary ogniska w nowoczesnych lampach rentgenowskich są rzędu ~0.1 mm. Okazuje się, że elektrony wnikające w anodę, mniej niż 1% swojej energii kinetycznej oddają w postaci promieniowania elektromagnetycznego. Pozostała część energii kinetycznej ulega konwersji w ciepło. Przykładowo dla anody wykonanej z wolframu i elektronów przyspieszonych napięciem 50 keV, tylko 0.4 % ich początkowej energii kinetycznej zostaje wyemitowana w postaci promieniowania X. Produkowane ciepło w lampach Rentgenowskich stanowi poważny problem dla konstrukcji tych urządzeń. W trakcie pracy anoda lampy może rozgrzać się do temperatury wyższej niż temperatura topnienia materiału z którego jest zbudowana, zwłaszcza że ciepło to powstaje głównie w bardzo małym obszarze ogniska. W celu rozwiązania problemu odprowadzania ciepła wprowadzonych zostało kilka rozwiązań:
- Anoda jest chłodzona wodą lub olejem, rozwiązanie to można stosować dla napięcia anodowego poniżej 40 kV, wtedy bowiem moc wydzielanego ciepła nie przekracza 2 kW i może zostać odprowadzona przez system chłodzący.
- Lampa z tzw wirującą anodą; rozwiązanie to umożliwia nie naświetlania jednego punktu na anodzie, tylko pierścienia o szerokości ogniska i długości. W wyniku wirowania anody, dane miejsce jest wystawione na zderzenia z elektronami tylko przez krótką chwilę czasu, po czym możliwe jest odprowadzenie z tego miejsca ciepła. Anoda rotuje z prędkością od 3600 do 10000 obrotów na minutę. Lampy z wirującą anodą umożliwiają odprowadzenie do 50 kW ciepła.
- Zwiększenie rozmiaru ogniska. W lampach Rentgenowskich stosowanych w medycynie obszar anody, który jest bombardowany przez elektrony może mieć większe rozmiary niż w standardowych lampach, co umożliwia lepsze odprowadzanie ciepła. W połączeniu z układami chłodzącymi oraz wirującą anodą, rozwiązanie to umożliwia zwiększenie napięcia przyspieszającego do maksymalnej wartości 150 kV. Uzyskanie promieniowania X o energii większej niż 150 - 160 keV przy pomocy lampy rentgenowskiej jest niemożliwe z uwagi na problem odprowadzania ciepła.
Opisane sposoby nie zawsze zabezpieczają anodę lampy rentgenowskiej przed przegrzaniem,w związku z tym nowoczesne urządzenia (zwłaszcza obrazowania medycznego) wyposażone są w systemy kontrolujące temperaturę lampy i wyłączające aparaturę, na określony czas, jeśli przekroczyła ona pewien określony próg. Powoduje to oczywiście uciążliwe przestoje w pracy urządzenia diagnostycznego.
Osłabienie promieniowania X przez materię
W zakresie energii stosowanych w Obrazowaniu Medycznym promieniowanie Rentgenowskie oddziałuje z materia w procesach rozproszenia Rayleigh’a, Thomsona i Comptona oraz efekcie fotoelektrycznym. Każdy z tych procesów scharakteryzowany jest przez przekrój czynny σ. Przypominamy, wzór na osłabienie wiązki promieniowania w funkcji przebytej drogi:
gdzie:
[math]N[/math] — ilość centrów oddziaływania na jednostkę objętości.
Wprowadzone zostało również pojecie średniej drogi swobodnej:
oraz liniowy współczynnik osłabienia wiązki promieniowania:
Osłabienie natężenia promieniowania X w przypadku monoenergetycznej wiązki i przechodzenia przez ośrodek charakteryzującym się jednorodnym liniowym współczynnikiem osłabienia promieniowania μ wyraża następujący wzór:
gdzie:
[math]I_0[/math] — natężenie wiązki padającej na ośrodek,
[math]I[/math] — natężenie wiązki po pokonaniu w ośrodku drogi x.
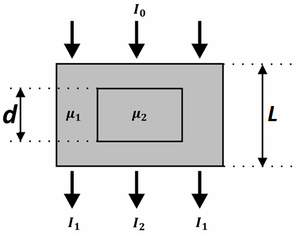
Jeżeli promieniowanie Rentgenowskie przechodzi przez ośrodki o różnym współczynniku μ (patrz rys. 10), wtedy wzór ( %i 16) przekształca się do postaci:
gdzie:
[math]I_i[/math] — natężenie promieniowania rentgenowskiego po przebyciu drogi x w i-tym ośrodku, charakteryzującym się liniowym współczynnikiem osłabienia promieniowania rentgenowskiego [math]\mu_i[/math]. Zanim promieniowanie rentgenowskie dotrze do i-tego ośrodka, przechodzi przez ośrodki o współczynniku osłabienia [math]\mu_1, \mu_2, \ldots, \mu_{i-1}[/math]. Przechodząc od struktur dyskretnych do ciągłych dostajemy:
Natężenie promieniowania Rentgenowskiego emitowanego przez Lampę Rentgenowską
Ogólnie natężenie promieniowania X produkowanego w Lampie Rentgenowskiej można opisać następującym wzorem:
gdzie:
- K — to pewna stała, zależna miedzy innymi od konstrukcji lampy,
- Z — to liczna atomowa materiału, z którego wykonana jest anoda,
- [math]I_A[/math] — natężenie prądu anodowego (przypominamy, że w lampie rentgenowskiej pomiędzy katodą a anodą poruszają się elektrony, mamy zatem do czynienia ze zjawiskiem przepływu prądu elektrycznego),
- [math]U_A[/math] — napięcie anodowe (przyspieszające).
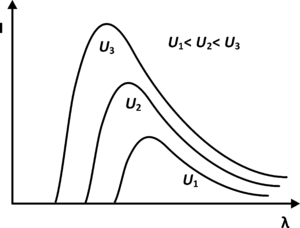
Na rys. 11 i rys. 12 zaprezentowano widmo natężenia promieniowania X w zależności od napięcia przyspieszającego i materiału z jakiego wykonana jest anoda. Musimy być również świadomi, że natężenie prądu anodowego [math]I_A[/math] zależy od ilości elektronów wyprodukowanych w zjawisku termoemisji, a to z kolei zależy od wielkości prądu płynącego przez katodę. Zależność ta jest proporcjonalna — w celu zwiększenia np. 3 krotnie wielkość prądu [math]I_A[/math] należy 3 krotnie zwiększyć wartość prądu płynącego przez katodę. Ponadto na natężenie prądu anodowego [math]I_A[/math] wpływa również napięcie przyspieszające [math]U_A[/math], jednak ta zależność nie jest proporcjonalna.
Kontrast obrazu uzyskanego przy pomocy promieniowania rentgenowskiego
Aby móc rozróżnić na obrazie jakąś strukturę, musi się ona charakteryzować się wartością parametru fizycznego, który odwzorowujemy na obrazie, istotnie różną od wartości struktur sąsiednich lub tła. Innymi słowy, do wyróżnienia struktur na obrazie potrzebny jest odpowiedni kontrast.Nie będziemy się w tym rozdziale zajmowali detektorami promieniowania rentgenowskiego. Interesuje nas na razie tylko, jaki teoretycznie możemy uzyskać kontrast na zdjęciu wykonanym przy pomocy promieniowania Rentgenowskiego. W tym celu załóżmy, iż wiązka promieniowania rentgenowskiego przechodzi przez ośrodek o grubości L i liniowym współczynniku promieniowania X równym [math]\mu_1[/math]. W ośrodku znajduje się struktura o grubości d i liniowym współczynniku osłabienia promieniowa X równym [math]\mu_2[/math] (patrz rys. 13). Wyznaczmy na początku kontrast lokalny:
gdzie:
[math]I_1[/math] — natężenie promieniowania po przejściu tylko przez ośrodek o współczynniku liniowego osłabienia promieniowania X równym [math]\mu_1[/math].
[math]I_2[/math] — natężenie promieniowania po przejściu przez ośrodki o współczynniku liniowego osłabienia promieniowania X równym [math]\mu_1[/math] i [math]\mu_1[/math].
Po wykonaniu prostych obliczeń otrzymujemy:
gdzie: [math]\Delta\mu=\left(\mu_2 - \mu_1\right)[/math]
Załóżmy teraz dla uproszczenia, że nasza struktura ma niewielkie rozmiary oraz różnica w liniowym współczynniku osłabienia promieniowanie X [math]\Delta\mu[/math] jest również niewielki, czyli gdy
wtedy:
zaś kontrast lokalny wynosi:
Kontrast lokalny zależy zatem od grubości struktury d oraz różnicy w liniowym współczynniku osłabienia promieniowania X pomiędzy interesującą nas strukturą i tłem.
Budowa Aparatury wykorzystywanej w Rentgenografii Klasycznej
Podstawowym elementem każdej aparatury rentgenowskiej jest oczywiście lampa rentgenowska, której budowa została omówiona we wcześniejszych rozdziałach. Kolejne podzespoły to:
- Filtry.
- Ogranicznik promieniowania (kolimator).
- Stół na którym umieszczany jest pacjent.
- Kratka przeciwrozproszeniowy.
- Detektor promieniowania.
Budowa oraz zasady funkcjonowania poszczególnych elementów (za wyjątkiem stołu) zostanie omówiona w osobnych podrozdziałach.
Filtry
Promieniowanie rentgenowskie emitowane przez lampę nie jest promieniowaniem monoenergetycznym. Zadaniem filtrów jest usuniecie z wiązki promieniowania, które nie może być wykorzystane do diagnostyki. Przede wszystkim jest to promieniowanie o energiach niższych niż 10 keV. Promieniowanie o energii poniższej 10 keV jest silne osłabiane przez ciało człowieka. W związku z tym ilość fotonów, która dotrze do detektorów jest zbyt mała, aby uzyskać wyraźny obraz. Innymi słowy, naświetlenie pacjenta promieniowaniem miękkim spowoduje obciążenie go dawką promieniowania jonizującego bez żadnych korzyści diagnostycznych. Filtry pełnią niezwykle istotną rolę w przypadku mammografii, co zostanie omówione w osobnym rozdziale.
Kolimator
Zadaniem kolimatora jest odpowiednie uformowanie kształtu wiązki promieniowania rentgenowskiego. W aparaturze diagnostycznej stosowane są głównie kolimatory nastawne, podczas gdy w radioterapii są to zwykle kolimatory stałe, wykonane z ołowianych blach o odpowiednio wykonanym kształcie. Szczególnym przypadkiem kolimatora nastawnego jest tzw. ogranicznik głębinowy. W jego przypadku, kształtowanie wiązki promieniowania przeprowadzane jest za pomocą układu co najmniej dwóch ograniczników nastawnych znajdujących się w różnych odległościach od ogniska lampy rentgenowskiej. Kolimatory nastawne są odpowiednio sprzężone ze sobą oraz ze stołem na którym umieszczony jest pacjent. Kolimatory głębinowy wytwarza wiązkę promieniowania o prostokątnym przekroju, i automatycznie dobierają jej rozmiar do rozmiaru detektora promieniowania X, którym najczęściej jest kaseta z filmem.
Kratka przeciwrozproszeniowa
Promieniowanie rentgenowskie oddziałuje z materią, z której zbudowany jest organizm ludzki, głównie w dwóch procesach:
- Efekcie Fotoelektrycznym,
- Zjawisku Comptona.
Efekt fotoelektryczny jest bardzo korzystny z punktu widzenia formowania obrazu. Skutkuje on bowiem absorpcją wyemitowaniem przez lampę fotonu rentgenowskiego. W przypadku Efektu Comptona, tylko część energii fotonu ulega absorpcji, zaś foton ulega rozproszeniu. Rozpraszanie Comptonowskie jest zatem bardzo niekorzystne w obrazowaniu medycznym i prowadzi do zaszumienia uzyskiwanych obrazów. Aby przeciwdziałać docieraniu do detektora promieniowania rentgenowskiego fotonów rozproszonych stosowane są specjalne kratki. Kratki te składają z pasków materiału silnie pochłaniającego promieniowanie rentgenowskie, umieszczonych w obudowie wykonanej z tworzywa sztucznego. Tak wykonana kratka może jednak rzucać cień na detektor promieniowania. Problem ten rozwiązano wprowadzając ruch kratki w trakcie wykonywania zdjęcia, co prowadziło do rozmazania obrazu kratki na zdjęciu rentgenowskim. Kratka ruchoma jest nazywana również kratką Buckego. Zastosowanie kratek przeciwrozproszeniowych podnosi kontrast około 3-4 krotnie.
Film i ekrany wzmacniające
Jak wiemy ludzkie oko nie jest czułe na promieniowanie X. W skład rentgenowskiej aparatury diagnostycznej musi zatem wchodzić układ, który dokona detekcji promieniowania X, utworzy obraz i umożliwi jego prezentację w zakresie światła widzialnego. Pierwszym detektorem promieniowania rentgenowskiego, który zresztą przyczynił się pośrednio do odkrycia tego promieniowania, była zwykła klisza fotograficzna. Do połowy lat 70 materiał z emulsją fotograficzną był naświetlany bezpośrednio promieniowaniem które opuściło pacjenta. Prowadzone badania wykazały jednak, że emulsja fotograficzna jest również bardzo mało czuła na promieniowanie X. Z drugiej strony emulacja fotograficzna jest bardzo czuła na promieniowanie z zakresu widzialnego. Postanowiono zatem, do układu detekcji wprowadzić materiał, który dokona konwersji promieniowania rentgenowskiego na światło widzialne. W tym celu wykorzystano zjawisko Luminescencji. Luminescencja (tzw. zimne świecenie, jarzenie) — zjawisko emisji fal świetlnych przez ciała (luminofor), wywołane inną przyczyną niż rozgrzanie ciała do wysokiej temperatury. Luminescencja obejmuje bardzo szeroki zakres zjawisk emisji promieniowania świetlnego, takich jak:
- Chemiluminescencja — Wytworzenie światła w trakcie niektórych reakcji chemicznych.
- Elektroluminescencja — Świecenie pod wpływem stałego lub zmiennego prądu elektrycznego.
- Elektronoluminescencja (katodoluminescencja) — Świecenie pod wpływem elektronów przyspieszanych napięciem między elektrodami (ten rodzaj wzbudzania ma liczne zastosowania w kineskopach, oscyloskopach, mikroskopach elektronowych itp.)
- Fotoluminescencja — Świecenie wywołane przez pochłonięcie promieniowania elektromagnetycznego z obszaru widzialnego, ultrafioletu lub podczerwieni. Pochłonięta energia jest następnie wyemitowana także w postaci światła, na ogół o energii mniejszej niż energia światła wzbudzającego. Ze względu na czas trwania fotoluminescencję dzieli się na:
- fluorescencję — zjawisko trwające wyłącznie podczas działania czynnika wzbudzającego,
- fosforescencję — zjawisko trwające również przez pewien czas po ustąpieniu czynnika wzbudzającego; substancje zdolne do fosforescencji nazywane są zwyczajowo fosforami.
- Scyntylacja — Emisja światła pod wpływem promieniowania jonizującego:
- rentgenoluminescencja — wywołana promieniowaniem rentgenowskim,
- radioluminescencja — świecenie pod wpływem promieniowania alfa α, beta β, gamma γ
Z punktu widzenia detekcji promieniowania rentgenowskiego w diagnostyce medycznej, najważniejszymi zjawiskiem jest scyntylacja, a w szczególności rentgenoluminescencja. W żargonie technicznym dotyczącym aparatury rentgenowskiej rzadko jednak mówi się o rentgenoluminescencja, stojąc terminy scyntylacja lub luminescencja. Należy jednak pamiętać jak szeroką klasę zjawisk obejmuje określenie luminescencji. Warto również wiedzieć, iż scyntylacja jest jednym z rodzajów Fotoluminescencji, w przypadku której wyróżniamy fluorescencję oraz fosforescencję, które w zależności od dalszych procesów zachodzących w trakcie detekcji promieniowania rentgenowskiego mogą wpływać korzystnie lub niekorzystnie na powstawanie obrazu. Opiszemy teraz rozwiązania techniczne, które umożliwiły wykorzystanie zjawiska luminescencji do detekcji promieniowania X.
Luminofor nanoszony jest na powierzchnię wykonaną z tworzywa sztucznego, tworząc tzw. ekran wzmacniający. Pomiędzy dwa ekrany wzmacniające wprowadzany jest film pokryty obustronnie emulsją fotograficzną. Całość (dwa ekrany wzmacniające oraz film) tworzy tzw. kasetę. W celu podwyższenia skuteczności konwersji promieniowania X na światło stosowane są dodatkowe rozwiązania. Przede wszystkim, powierzchnię na której ma być umieszczony luminofor pokrywa się najpierw warstwą odbijającą światło. Wiadomo, że światło, wytworzone w luminoforze pod wpływem promieniowania X będzie emitowane we wszystkich kierunkach. W związku z tym, do kliszy fotograficznej dotrze tylko 50% światła widzialnego. Zadaniem warstwy odbijającej ekranu wzmacniającego jest ponowne skierowanie światła w kierunku emulsji fotograficznej. Należy jednak pamiętać, iż na jakość otrzymywanego w diagnostyce medycznej obrazu mają wpływ głównie dwa parametry — kontrast oraz rozdzielczość przestrzenna. Nie zawsze jest możliwe polepszanie wartości obydwu tych parametrów na raz, czego przykładem są właśnie układy ekran wzmacniający — emulsja fotograficzna. Stosowanie filmu obustronnie pokrytego emulsją światłoczułą, zastosowanie dwóch ekranów wzmacniających oraz warstw odbijających zwiększa skuteczność konwersji promieniowania X na światło widzialne. Z drugiej strony w układzie takim powstają wielokrotne odbicia, które powodują rozmazanie obrazu, jeśli światło padające na jedną stronę kliszy nie zostanie przez nią zaabsorbowane, utworzy obraz po drugiej stronie również skutkując rozmazaniem obrazu. Ponadto gruba warstwa luminoforu prowadzi także do rozproszenia światła i dalszej degradacji jakości obrazu. W związku z tym kasety dostępne są w różnych konfiguracjach, charakteryzujących się różną grubością ziarna luminofora i grubością warstwy luminofora, rodzajem filmu (jednostronnie lub dwustronnie pokrytego emulsją). Nie ulega jednak wątpliwości, iż zastosowanie kaset z ekranami wzmacniającymi korzystnie wpłynęło na jakość obrazów w diagnostyce medyczne, a także zredukowanie dawki promieniowania X pochłoniętej przez pacjenta (od około 20 do 100 razy).
Charakterystyka filmu
Jednym z najważniejszych parametrów charakteryzujących filmy wykorzystywane w klasycznej diagnostyce rentgenowskiej jest tzw. gęstość optyczna. Zrozumienie tego parametru oraz jego zależność od ekspozycji umożliwi również zrozumienie przyczyn intensywnych badań nad detektorami cyfrowymi, które wypierają filmy z zastosowań w diagnostyce medycznej. Zdefiniujmy na początku stopień zaczernienia filmu w wyniku ekspozycji. W tym celu możemy zmierzyć transmisję promieniowania przechodzące przez kliszę. Stopień zaczernienia filmu jest natężenia promieniowania przechodzącego przez klisze [math]I[/math] do natężenia padającego na kliszę [math]I_0[/math]:
Gęstość optyczna to:
Zakres gęstości optycznej zaprezentowano w poniższej tabeli:
| T | D | Skutek |
|---|---|---|
| 1 | 0 | Szczątkowe naświetlenie, będące np. efektem przypadkowej emisji światła przez kasetę. |
| 0.1 | 1 | Film szarawy. |
| 0.01 | 2 | Film zaczerniony. |
| 0.001 | 3 | Film bardzo zaczerniony. |
| 0.00025 | 3.6 | Maksymalne zaczernienie stosowane w diagnostyce medycznej. |
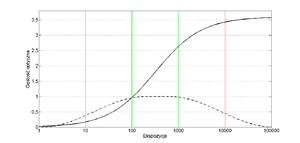
Użyteczny zakres gęstości optycznej to 0.5 – 2.2. Wprowadźmy teraz pojęcie ekspozycji. Ekspozycja to ilość promieniowania padającego na detektor w trakcie wykonywania zdjęcia. Wielkość ta, co jest oczywiste, będzie zależeć zarówno od natężenie promieniowania padającego oraz czasu wykonywania zdjęcia. Na rysunku rys. 14 zaprezentowano zależność gęstości optycznej od ekspozycji, którą nazywamy Krzywą Charakterystyczną Filmu. Jak można zauważyć, zależność ta tylko w pewnym obszarze jest liniowa. Tymczasem kontrast obrazu uzyskiwanego na kliszy to nachylenie (pochodna) gęstości optycznej względem ekspozycji. Na rysunku rys. 14. możemy wyróżnić trzy obszary Krzywą Charakterystyczną Filmu:
- obszar, w którym gęstość optyczna jest niewielka i słabo zależy od ekspozycji — jest to obszar w którym film jest niedoświetlony,
- obszar, w którym gęstość optyczna jest duża i słabo zależy od ekspozycji — jest to obszar w którym film jest prześwietlony,
- obszar, w którym gęstość optyczna zależy liniowo od ekspozycji — w tym obszarze kontrast jest stały.
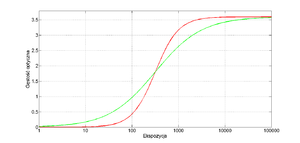
Nieliniowa zależność gęstości optycznej od ekspozycji to jedna z głównych wad filmów, co prześledzimy na następującym przykładzie. Załóżmy iż wykonujemy zdjęcie rentgenowskie dwóch tkanek pacjenta — A i B, które znacznie różnią się liniowym współczynnikiem osłabienia promieniowania X. Tkanka A silnie tłumi promieniowanie X, podczas gdy tkanka B osłania to promieniowanie nieznacznie. Kontrast uzyskanego zdjęcia jest funkcją ekspozycji. Z kolei ekspozycja zależy od natężenia promieniowania padającego na kliszę. Natężenie promieniowania, które dociera do kliszy, zależy od stopnia jego osłabienia przez narządy. Chcąc dobrze odwzorować tkankę B, film powinien być naświetlany krótko, gdyż tkanka ta niewiele osłabia promieniowanie. Z kolei w przypadku tkanki A, która silnie osłabiła promieniowanie rentgenowskie, czas ekspozycji powinien być wydłużony. Niestety, tylko pewien ograniczony zakres ekspozycji prowadzi do wytworzenia odpowiedniego kontrastu. Starając się dobrać ekspozycję jednocześnie dla tkanki A i B można łatwo doprowadzić do prześwietlenia lub niedoświetlania filmu. Pewnym rozwiązaniem tego problemu jest wytworzenie filmu o jak szerszym zakresie liniowej zależności gęstości optycznej od ekspozycji. W takim przypadku jednak gęstość optyczna będzie narastać wolno, a w związku z tym i kontrast (który jest pochodzą gęstości optycznej po ekspozycji) będzie miał małą wartość. W zależności, na którym parametrze bardziej nam zależy, czy wysokim kontraście, czy szerszym zakresie użytecznej ekspozycji wytworzono różne rodzaje filmu, charakteryzowane dodatkowymi parametrami. W podsumowaniu tego rozdziału wymienimy cztery najważniejsze:
- Kontrast — Zakres ekspozycji w którym gęstość optyczna zmienia się liniowo. Filmy o szeroki zakresie użytecznej ekspozycji są tzw. filmami o małej dynamice kontrastu. Z kolei filmy o wąskim zakresie użytecznej ekspozycji to filmy o tzw. dużej dynamice kontrastu, które jednakże łatwo prześwietlić lub nie doświetlić.
- Średni kontrast (ang Average Contrast):
- Gamma — kontrast maksymalny.
- Szybkość uzyskania gęstości optycznej D = 1:
System sterowania ekspozycją
W rozdziale [3] wprowadzone zostało pojęcie ekspozycji,która jest miarą ilości fotonów padających na detektor promieniowania. Ekspozycja zależy od natężenia promieniowania oraz czasu wykonywania badania. Przypominamy, że z kolei natężenie promieniowania rentgenowskiego zależy od materiału z którego wykonana jest anoda, napięcia przyspieszającego [math]U_A[/math] i natężenia prądu anodowego [math]I_A[/math] (wzór (Equation 19)). Z kolei natężenie prądu anodowego również zależy od napięcia przyspieszającego [math]U_A[/math], a także materiału z którego wykonana jest katoda oraz natężenia prądu płynącego przez katodę i wywołującego zjawisko termoemisji. Podsumowując, ekspozycja zależy od wielu parametrów, które należy właściwie ustawić. W zależności od tego, które z parametrów są ustawiane automatycznie lub może regulować je technik prowadzący badania wyróżniamy cztery techniki:
- Technika Trzypunktowa — napięcie anodowe [math]U_A[/math], prąd anodowy [math]I_A[/math] i czas wykonywania naświetlenia technik ustawia ręcznie. Przypominamy, że natężenie prądu anodowego [math]I_A[/math] zależy zarówno on natężenia prądu płynącego przez katodę [math]I_K[/math]jak i napięcie przyspieszającego [math]U_A[/math]. Jednakże prąd [math]I_A[/math] jest proporcjonalny do prądu [math]I_K[/math] w związku z tym regulacja prądu anodowego odbywa się głównie poprzez zmiany prądu płynącego przez katodę.
- technika dwupunktowa — w przypadku tej techniki wprowadza się dodatkową wielkość — miliampero-sekundy (mAs):
gdzie [math]I_A[/math] — prąd anodowy (prąd płynący od anody do katody), [math]s[/math] — czas wykonywania ekspozycji. Przykładowo, jeśli prąd anodowy [math]I_A[/math] wynosi 400 mA, zaś czas ekspozycji 500 ms, to współczynnik mAs = 200 mAs. Operator ustawia ręcznie dwa parametry napięcie przyspieszające i parametr mAs.
- technika jednopunktowa — operator ustawia ręcznie wartość napięcia przyspieszającego, pozostałe parametry dobiera automat na podstawie sygnału, umieszczonych przed kasetą, z detektorów promieniowania,
- technika zero-punktowa — wszystkie parametry są dobierane automatycznie
Wzmacniacze Obrazu
Niezwykle ważne w diagnostyce medycznej jest uzyskiwanie obrazów w czasie rzeczywistym. Do lat 50-tych ubiegłego wieku w celu uzyskiwania takich obrazów stosowano ekrany fluoroskopowe. Wadą tych ekranów była niewielka jasność i kontrastowa, przez co lekarz musiał adaptować wzrok do ciemności panującej w pokoju w którym przeprowadzano badanie. Ekrany fluoroskopowe zastąpiono wzmacniaczami obrazu, jednakże do dzisiaj w radiologii funkcjonuje nazwa „fluoroskopia”.
Budowa i zasada działania wzmacniacza obrazu
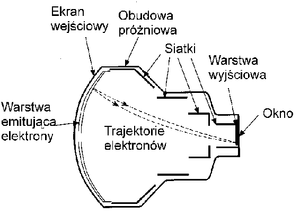
Schemat wzmacniacza obrazu zaprezentowano na rys. 16, podstawowe elementy to luminofor wejściowy, fotokatoda, układy przyspieszające wraz z optyką elektronowa, luminofor wyjściowy.
- Luminofor wejściowy konwertuje promieniowanie rentgenowskie na promieniowanie widzialne. Materiałem wykorzystywanym w procesie luminescencji to jodek cezu (CsI) domieszkowanego sodem (Na), który umieszcza się na podłożu aluminiowym. Kryształy (CsI:Na) pod wpływem absorpcji promieniowania X świecą światłem niebieskim Światło to dociera następnie do fotokatody.
- Fotokatoda — pod wpływem światła emitowanego przez luminofor emituje elektrony.
- Układy przyspieszające i optyka elektronowa. Wytworzone przez katodę elektrony są przyspieszane napięciem 25 keV do 35 keV oraz ogniskowane przez odpowiednio skonfigurowaną optykę elektronową.
- Luminoforu Wyjściowy Luminofor emituje, w odpowiedzi na absorpcje elektronów, zielone światło. Dodatkowo, na warstwę luminoforu nałożona jest cienka warstwa aluminium, która jest jednocześnie anodą układu.
Detektory Cyfrowe
Detektory cyfrowe można podzielić na dwie grupy i skojarzone z nimi metody klasycznej radiografii:
- Radiografia fosforowa (tzw. półcyfrowa),
- Radiografia cyfrowa bezpośrednia.
Detektory cyfrowe promieniowania X zostały opracowane w roku 1987 przez Francisa Mouyena. System obrazowania oparty na tych detektorach zaprezentowano dwa lata później a opatentowano pod nazwą radiowizjografia. Nazwa ta jest zastrzeżona dla produktów firmy Trophy Radiologie. Inne firmy stosują nazwę radiografii cyfrowej. Innymi słowy: Radiowizjografia = Radiografia cyfrowa bezpośrednia.
Radiografia półcyfrowa (ang. Computed Radiography, CR)
W latach 80-tych wprowadzono technologię, umożliwiającą wygodną akwizycję zdjęć rentgenowskich na cyfrowych nośnikach danych i ich analizę obrazu na ekranie komputerowym. Technologia ta wykorzystuje kasety kompatybilne z kasetami przeznaczonymi dla klasycznych filmów, jednakże wewnątrz kasety zamiast materiału z emulsją światłoczułą znajdował specjalny fotoczuły ekran fosforowy. Pod wpływem promieniowania X elektrony w atomach wchodzących w skład ekranu wchodziły na wyższe poziomy energetyczne. Cechą charakterystyczną zastosowanego materiału jest fakt, iż powrót atomów ze stanu wzbudzonego do stanu podstawowego nie następuje gwałtownie szybko. Atomy pozostają w stanie wzbudzonym dopóki nie zostaną z niego wytrącone np. za pomocą światła laserowego. Obraz diagnostyczny zapisany w ten sposób nazywamy obrazem utajonym, zaś stan w którym znajdują się atomy stanem metastabilnym. Po zakończeniu badania, kaset naświetlana jest światłem laserowym, elektrony uwolnione ze stanu metastabilnego emitują światło, które następnie jest odbierane i wzmacniane przez fotopowielacz. Wzmocnione światło jest następnie zamieniane na sygnał cyfrowy. Po zeskanowaniu obrazu kaseta jest kasowana za pomocą specjalnej lampy i może być użyta po raz ponowny.
Radiografia cyfrowa (ang. Digital Radiography, DR)
Pod koniec lat osiemdziesiątych ubiegłego wieku do stomatologii zostały wprowadzone pierwsze detektory umożliwiające uzyskanie zdjęcia rentgenowskiego bez wykonywania pośrednich kroków, takich jak np. skanowanie filmu. Wynalazca metody — Francis Mouyen, opatentował swoje odkrycie pod nazwą radiowizjografia (radio — wytwarzającego promieniowanie, visio — rejestrującego obraz, graphy — wyświetlającego obraz). Obecnie różnorodne formy cyfrowej detekcji promieniowania X określone są jako Radiografia Cyfrowa (ang. Digital Radiography, DR) lub Radiografia Bezpośrednia. Dotychczas opracowana kilka rodzajów detektorów cyfrowych, z których omówimy najważniejszy — detektor wykorzystujący amorficzny krzem.
Podstawowym elementem w radiografii cyfrowej jest matryca detektorów (ang. Flat Panel Detectors, FPDs). Pojedynczy detektor, odpowiedzialny za wytworzenie jednego piksela na obrazie, składa się z:
- fotodiody wykonanej z amorficzngo krzemu,
- materiału scyntylacyjnego — warstwy jodku cezu,
- układu regulującego.
Amorficzny krzem z uwagi na swoje właściwości jest masowo wykorzystywany w budowie ekranów LCD oraz ogniw fotogalwanicznych. Wśród jego zalet można wymienić m.in:
- Duży współczynnik absorpcji i transmisji promieniowania elektromagnetycznego w zakresie widzialnym.
- Prosta technologia otrzymywania.
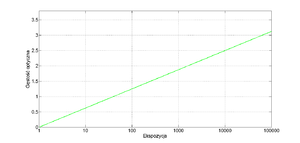
Rolą fotodiody wykonanej z amorficznego krzemu jest konwersja promieniowania elektromagnetycznego na ładunek.Niestety, tego rodzaju fotodiody są bardzo słabo czułe na promieniowanie rentgenowskie, dlatego pokrywa się je materiałem scyntylacyjnym, jakim jest jodek cezu. Pod wpływem promieniowania świetlnego w fotodioda wytwarza ładunek elektryczny wprost proporcjonalny do ilości padających na detektor fotonów rentgenowskich. Jest to niezwykle istotna zaleta detektorów cyfrowych, dzięki której zależność "zaczernienia" obrazu jest liniową funkcją ekspozycji (patrz rys. 17). W przypadku radiografii klasycznej zależność ta była nieliniowa. Ładunek wytworzony przez fotodiodę jest gromadzony w elemencie pojemnościowym a następnie odczytywany przez odpowiednie układy elektroniczne wchodzące w skład matrycy.