Obrazowanie:Obrazowanie Medyczne/Rentgenowska Tomografia Komputerowa

Rentgenowska Tomografia Komputerowa

Rentgenowska Tomografia Komputerowa (ang. Computed Tomography, CT), nazywana w żargonie medycznym po prostu tomografią, była historycznie pierwszą metodą umożliwiającą uzyskanie obrazów wybranych warstw pacjenta. Poprzedni rozdział zakończyliśmy pytaniem jak aparatura medyczna może zrealizować Transformatę Radona. Okazuje się, że przy pomocy odpowiednio skolimowanej wiązki promieniowania Rentgenowskiego oraz ruchów lampy rentgenowskiej i detektorów, procesy fizyczne zachodzące w trakcie transmisji promieniowania X przez pacjenta automatycznie prowadzą do wyznaczania Transformaty Radona.

Podstawy Rentgenowskiej Tomografii Komputerowej

Schemat układu pomiarowego, fizycznie realizującego Transformatę Radona. Lampa Rentgenowska emituje wiązkę promieniowania X, przebiegającą przez w odległości t od środka układu współrzędnych. Wiązka ta tworzy kąt φ z osią X. Po dokonaniu pojedynczego pomiaru (skanu) lampa RTG wraz z detektorem przesuwa się wzdłuż do osi T, dokonując kolejnych pomiarów. Po przeskanowaniu obiektu wzdłuż danego kierunku, lampa RTG i detektor obracają się o pewien kąt, a następnie ponownie wykonują ruchy translacyjne.

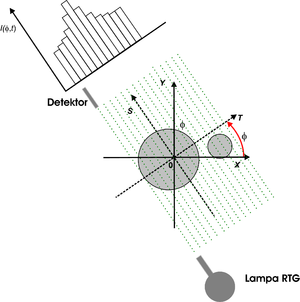
Niech badany obiekt charakteryzuje się pewnym rozkładem liniowego współczynnika osłabienia promieniowania X [math]\mu(x, y)[/math], który jest niezerowy w obrębie obiektu i równy 0 wszędzie poza nim. Obiekt opisany jest we współrzędnych kartezjańskich X-Y, zaś pozycja lampy Rentgenowskiej oraz detektora w obróconym układzie współrzędnych T-S. Związki pomiędzy tymi układami są następujące:

[math] \left\{ \begin{array}{l} t = x\cos(\phi) + y\sin(\phi) \\ \\ s = -x\sin(\phi) + y\cos(\phi) \\ \end{array} \right. [/math]

[math] \left\{ \begin{array}{l} x = t\cos(\phi) - s\sin(\phi) \\ \\ y = t\sin(\phi) + s\cos(\phi) \\ \end{array} \right. [/math]

Przypomnimy teraz prawo osłabienia promieniowania Rentgenowskiego przy przejściu przez ośrodek charakteryzujący się niejednorodnym linowym współczynnikiem osłabienia promieniowania X. Załóżmy, iż mamy do czynienia, ze skolimowaną wiązką promieniowania (tzw. pencil beam), która biegnie wzdłuż osi X. Niech obiekt również rozciąga się również tylko wzdłuż tej osi. Wtedy natężenie promieniowania opuszczającego obiekt będzie wynosić:

[math] I = I_0e^{-\int_{-\infty}^{\infty}\mu(x)dx} [/math]

W diagnostyce medycznej chcemy zobrazować jednak wybrane warstwy pacjenta, czyli obiekty dwuwymiarowe. Jeśli obiekt opisany jest w kartezjańskim układzie współrzędnych, to liniowy współczynnik osłabienia promieniowania Rentgenowskiego będzie zależał zarówno od współrzędnej X jak i Y. Utrudni to znacznie rekonstrukcję obrazu. Tymczasem aparat matematyczny wprowadzony w poprzednim rozdziale (parametryzacja prostej w biegunowym układzie współrzędnych, obrót układu współrzędnych), idealnie pasuje to rozważanego problemu. Przyjmijmy teraz iż dokonujemy badania obiektu dwuwymiarowego. Aparatura pomiarowa składa się z lampy Rentgenowskiej i pojedynczego detektora. Lampa Rentgenowska emituje skolimowaną wiązkę promieniowania X. Wiązka ta penetruje obiekt i trafia do detektora. Układ zaprezentowano na rys. 1. Proszę zauważyć, iż wiązka promieniowania biegnąca od lampy RTG do detektora tworzy linię prostą. Można również zaobserwować pewne podobieństwa pomiędzy rys. 1 a rys. [1]. Jak się okaże, nie jest to tylko podobieństwo graficzne. Układ zarejestrowany na rys. 1 realizuje Transformatę Radona, co za chwile wykażemy. Przebieg wiązki promieniowania, która łączy lampę RTG z detektorem można opisać za pomocą parametrów [math]t[/math] (odległość prostej od początku układu współrzędnych) i kąta φ, jaki tworzy normalna do prostej względem osi X (patrz rozdział Parametryzacja Prostej). Wynik pojedynczego pomiaru, dla ustalonego kąta [math]\phi[/math] ustawienia lampy i detektora względem osi X, oraz jej przesunięcia [math]t[/math] względem początku układu współrzędnych będziemy nazywać skanem i jest on równy:

[math] I(\phi,t) = I_0e^{-\int_{-\infty}^{\infty} \mu(t\cos(\phi)-s\sin(\phi),t\sin(\phi)+s\cos(\phi))ds} [/math]

wprowadzają oznaczenie:

[math] \mu(t\cos(\phi)-s\sin(\phi),t\sin(\phi)+s\cos(\phi)) \equiv \mu(t,s) [/math]

otrzymujemy zależność:

[math] I(\phi,t) = I_0e^{-\int_{-\infty}^{\infty} \mu(t,s)ds} [/math]

W tym miejscu możemy zauważyć korzyść z rozważania problemu w układzie T-S związanego z lampą RTG i detektorem, a nie pacjentem — w tym układzie współrzędnych dokonujemy całkowania wzdłuż prostej równoległej do osi S, a zatem całkujemy funkcję jednowymiarową. Przekształcając powyższe równanie dostajemy:

[math] \ln\left(\frac{I_0}{I(\phi,t)}\right) = \int_{-\infty}^{\infty}\mu(t,s)ds [/math]

Co jest niczym innym jak Transformatą Radona badanego obiektu.

Zbiór jednowymiarowych pomiarów (skanów) dokonanych dla różnych pozycji lampy [math]t[/math] ale tego samego kąta nazywamy rzutem lub projekcja (ang. projection) i oznaczymy [math]P(\phi)[/math]. Projekcja jest tożsama z transformatą Radona obiektu wykonaną dla określonego kąta. Lampa Rentgenowska emitująca skolimowaną wiązkę promieniowania X i detektor przeprowadza fizyczną realizację transformaty Radona. Otrzymujemy serię pomiarów, na podstawie których możemy zrekonstruować obraz obiektu, posługując się np. odwrotną Transformatą Radona. Jest to jednak sposób nieefektywny numerycznie, dlatego zostały opracowane inne metody rekonstrukcji obrazu, cały czas jednak opierające się na pomiarach zebranych w wyżej opisany sposób. W dalszej części materiałów opiszemy jedną z tych metod.

Metoda algebraiczna rekonstrukcji obrazów

Przeprowadźmy dyskretyzację równania Equation 7 w następujący sposób:

• Dzielimy obiekt na [math]N[/math]x[math]N[/math] kwadratowych obszarów, gdzie [math]N[/math] = 256, [math]N[/math] = 512 [math]N[/math] = 1024, w wyniku czego obliczanie funkcji [math]\mu(t,s)[/math] odbywa się dla dyskretnego zbioru wartości [math]\mu(t_k,s_k)[/math].
• Lampa i detektor obracają się o kąt [math]\Delta\phi[/math] i przesuwają o o [math]\Delta t[/math]. Skan dokonany dla zadanego [math]i[/math]-tego kąta oraz [math]j[/math]-tego przesunięcia oznaczymy: [math]P(i\cdot\Delta\phi,j\cdot\Delta t) = P(\phi_i,t_j)[/math]. Z kolei projekcję wykonaną dla [math]i[/math]-tego kąta [math]P(\phi_i)[/math].
• Przy podziale obiektu na piksele trzeba uwzględnić poprawkę [math]w_{\phi_i,t_j}(t_j,s_k)[/math] związaną z tym, iż promień skolimowanej wiązki emitowany przez RTG, przechodząc przez piksele pod różnymi kątami (odpowiadającymi kolejnym projekcjom i kolejnym położeniu lampy), pokrywa różne ich powierzchnie. Poprawkę tę można wyliczyć w następujący sposób:
  

[math] w_{\phi_i,t_j}(t_j,s_k) = \frac{S_p(\phi_i,t_j)}{S_e(t_j,s_k)} [/math]

gdzie:
[math]S_p(\phi_i,t_j)[/math] — pole powierzchni promienia rentgenowskiego dla zadanego skanu [math]\phi_i[/math] i przesunięcia lampy [math]t_j[/math] w obrębie przyjętego, najmniejszego elementu [math](t_i, s_k)[/math] obiektu,
[math]S_e(t_k,s_k)[/math] — pole powierzchni elementu o współrzędnych [math](t_j, s_k)[/math].

Przejdźmy teraz do opisu obiektu w układzie współrzędnych [math]T-S[/math] i rozważmy projekcję dla pewnego zadanego [math]i[/math]-tego kąta, [math]\phi_i = i\cdot\Delta\phi[/math]. Dyskretna postać równania Equation 7, odpowiadająca jednemu skanowi, będzie następująca:

[math] P(\phi_i,t_j) = \sum_{k=1}^N\mu(t_j,s_k) [/math]

Musimy jednak wprowadzić poprawkę na bieg promienia przez poszczególne piksele. W ogólności skolimowana wiązka rentgenowska może przebiegać przez więcej niż [math]N[/math] pikseli. Założymy, iż promień może przebiegać przez cały obiekt, czyli n=NxN pikseli:

[math] P(\phi_i,t_j) = \sum_{k=1}^n\sum_{l=1}^nw_{\phi_i,t_j}(t_k,s_l)\mu(t_k,s_l) [/math]

W powyższym równaniu, odpowiadającym pojedynczemu skanowi, potrzebujemy [math]NxN[/math]. Dla zadanego kąta [math]\phi_i[/math] wykonujemy jednak N skanów, tworzących jedną projekcję:

[math] P(\phi_i) = \left\{ \begin{array}{l} P(\phi_i,t_1) = \sum_{k=1}^n\sum_{l=1}^nw_{\phi_i,t_1}(t_k,s_l)\mu(t_k,s_l) \\ \\ P(\phi_i,t_2) = \sum_{k=1}^n\sum_{l=1}^nw_{\phi_i,t_2}(t_k,s_l)\mu(t_k,s_l) \\ \\ \vdots \\ \\ P(\phi_i,t_i) = \sum_{k=1}^n\sum_{l=1}^nw_{\phi_i,t_i}(t_k,s_l)\mu(t_k,s_l) \\ \\ P(\phi_i,t_N) = \sum_{k=1}^n\sum_{l=1}^nw_{\phi_i,t_N}(t_k,s_l)\mu(t_k,s_l) \end{array} \right. [/math]

Pojedyncza projekcja wymaga już [math]N^3[/math] wag. Wykonujemy ponadto [math]N[/math] projekcji:

[math] \begin{array}{l} P(\phi_1) = \left\{ \begin{array}{l} P(\phi_1,t_1) = \sum_{k=1}^n\sum_{l=1}^nw_{\phi_i,t_1}(t_k,s_l)\mu(t_k,s_l) \\ \\ P(\phi_1,t_2) = \sum_{k=1}^n\sum_{l=1}^nw_{\phi_i,t_2}(t_k,s_l)\mu(t_k,s_l) \\ \\ \vdots \\ \\ P(\phi_1,t_i) = \sum_{k=1}^n\sum_{l=1}^nw_{\phi_i,t_i}(t_k,s_l)\mu(t_k,s_l) \\ \\ P(\phi_1,t_N) = \sum_{k=1}^n\sum_{l=1}^nw_{\phi_i,t_N}(t_k,s_l)\mu(t_k,s_l) \end{array} \right.\\ \\ \vdots \\ \\ P(\phi_i) = \left\{ \begin{array}{l} P(\phi_i,t_1) = \sum_{k=1}^n\sum_{l=1}^nw_{\phi_i,t_1}(t_k,s_l)\mu(t_k,s_l) \\ \\ P(\phi_i,t_2) = \sum_{k=1}^n\sum_{l=1}^nw_{\phi_i,t_2}(t_k,s_l)\mu(t_k,s_l) \\ \\ \vdots \\ \\ P(\phi_i,t_i) = \sum_{k=1}^n\sum_{l=1}^nw_{\phi_i,t_i}(t_k,s_l)\mu(t_k,s_l) \\ \\ P(\phi_i,t_N) = \sum_{k=1}^n\sum_{l=1}^nw_{\phi_i,t_N}(t_k,s_l)\mu(t_k,s_l) \end{array} \right.\\ \\ P(\phi_N) = \left\{ \begin{array}{l} P(\phi_N,t_1) = \sum_{k=1}^n\sum_{l=1}^nw_{\phi_N,t_1}(t_k,s_l)\mu(t_k,s_l) \\ \\ P(\phi_N,t_2) = \sum_{k=1}^n\sum_{l=1}^nw_{\phi_N,t_2}(t_k,s_l)\mu(t_k,s_l) \\ \\ \vdots \\ \\ P(\phi_N,t_i) = \sum_{k=1}^n\sum_{l=1}^nw_{\phi_N,t_i}(t_k,s_l)\mu(t_k,s_l) \\ \\ P(\phi_N,t_N) = \sum_{k=1}^n\sum_{l=1}^nw_{\phi_N,t_N}(t_k,s_l)\mu(t_k,s_l) \end{array} \right. \end{array} [/math]

a zatem ostatecznie potrzebujemy [math]N^4[/math] wag. Dla najniższej stosowanej w Tomografii liczby pikseli, [math]N=256[/math] przechowanie samych wag, wymagałoby [math]256^4\cdot 8[/math] bajtów pamięci, tj. 32 GB. Ponadto rozwiązanie układu równań, w którym macierz wag wypełniona byłaby bardzo często zerami prowadzi do niestabilności numerycznych. Kolejną wadą takiego podejścia jest możliwość dokonania rekonstrukcji dopiero po zakończeniu wszystkich pomiarów.

Metody Iteracyjne

Idea metod iteracyjnych polega na wstępnym założeniu pewnej postaci funkcji [math]\mu(t,s)[/math] (np. może to być średni pacjent lub też można założyć obiekt jednorodny), a następnie symulowaniu procesu skanowania i porównywaniu wyniku z symulacji z rzeczywistymi wynikami pomiaru. Na podstawie różnicy wyników otrzymanych z tych dwóch źródeł oblicza się poprawkę do rozkładu początkowego. Wprowadźmy następujące oznaczenia, pomijając dla uproszczenia notacji dyskretyzację równań:

• [math]\mu(t,s)[/math] — rzeczywisty rozkład liniowego współczynnika osłabienia promieniowania X,
• [math]\mu^n(t,s)[/math] — wyliczony w [math]n-tej[/math] iteracji rozkład liniowego współczynnika osłabienia promieniowania X,
• [math]P(\phi,t) = \sum_{t}\sum_{s}w_{\phi,t}(t,s)\mu(t,s)[/math] — zmierzona wartość skanu
• [math]P^n(\phi,t) = \sum_{t}\sum_{s}w_{\phi,t}(t,s)\mu(t,s)[/math] — wyliczona w [math]n[/math]-tej iteracji wartość skanu.

Błąd pomiędzy rzeczywistą a wyliczoną na drodze iteracji wartości wszystkich skanów wynosi:

[math] \epsilon = \sum_\phi\sum_t(P^n(\phi,t)-P(\phi,t))^2 [/math]

i oczekujemy, że wraz z dokonywaniem kolejnych poprawek dla [math]P^n(\phi,t)[/math] będzie dążył do zera. Z warunku minimalizującego funkcję błędu dostajemy:

[math] \Delta \mu^n(t,s) = \mu^n(t,s) - \mu^{n-1}(t,s) = \frac{(P(\phi,t) - P^n(\phi,t))\cdot w_{\phi,t}(t,s)}{\sum_{t}\sum_{s}(w_{\phi,t}(t,s)\mu(t,s))^2} [/math]

Po przekształceniu powyższego wzoru dostajemy:

[math] \mu^n(t,s) = \mu^{n-1}(t,s) + \Delta \mu^n(t,s) = \mu^{n-1}(t,s) + \frac{(P(\phi,t) - P^n(\phi,t))\cdot w_{\phi,t}(t,s)}{\sum_{t}\sum_{s}(w_{\phi,t}(t,s)\mu(t,s))^2} [/math]

Problem — kiedy dokonać aktualizacji wartości [math]\mu^n(t,s)[/math]. Rozwiązanie — dwa podejścia: 1. Simultaneous Iterative Reconstruction Technique — SIRT. W podejściu SIRT, po wyliczeniu korekty dla danego piksela [math]\mu^n(t,s)[/math] natychmiast uaktualniana jest jego wartość, tak że wyliczane kolejne piskele, nawet dla tej samej projekcji, korzystają już z wartości zaktualizowanej. 2. Algebraic Reconstruction Technique — ART. W tym podejściu najpierw wyliczane są wszystkie poprawki dla danej projekcji. Ponieważ każda projekcja składa się z wielu skanów, dla zadanego piksela można otrzymać wiele poprawek. Z tych poprawek obliczana jest średnia korekta, o którą poprawia się zdany piksel.

Istnieje jeszcze wiele innych podejść iteracyjnych. Stosuje się również inne podejścia dla wag, np. jeśli promień przechodzi przez środek piksela jego waga wynosi 1, inaczej wynosi 0. Wtedy suma wag kwadratów w mianowniku jest równa liczbie pikseli, przez środek których przechodzi wiązka. Współczynnik taki oznaczmy przez [math]L(\phi,t)[/math].

[math] \mu^n(t,s) = \mu^{n-1}(t,s) + \Delta \mu^n(t,s) = \mu^{n-1}(t,s) + \frac{(P(\phi,t) - P^n(\phi,t))\cdot w_{\phi,t}(t,s)}{L(\phi,t)} [/math]

Przykład.
Przykład ten pochodzi z podręcznika Obrazowanie Biomedyczne pod redakcją L. Chmielewskiego, J. L. Kulikowskiego i A. Nowakowskiego.
Niech obiekt zostanie podzielony na dwa 4 piksele. Rozkład współczynnika osłabienia promieniowania X jest następujący:

[math] \begin{array}{|c|c|} 1 & 2 \\ - & - \\ 3 & 4 \end{array} [/math]

Będziemy dokonywać projekcji dla kąta [math]\phi = 270[/math] stopni i [math]\phi = 180[/math] stopni. Dostajemy następujące wartości skanów:

• dla kąta [math]90^0[/math]: 3, 7,
• dla kąta [math]180^0[/math]: 4, 6,

W zerowym kroku zakładamy jednorodny obiekt, o liniowym współczynniku osłabienia promieniowania równym średniej z wartości z którejś projekcji. Dla obydwu projekcji średnia ta wynosi 2.5, a zatem rozkład liniowego współczynnika osłabienia promieniowania X jest zatem równy:

[math] \begin{array}{|c|c|} 2.5 & 2.5 \\ - & - \\ 2.5 & 2.5 \end{array} [/math]

Nowe wartości projekcji wynoszą: Będziemy dokonywać projekcji dla kąta [math]\phi = 270[/math] stopni i [math]\phi = 180[/math] stopni. Dostajemy następujące wartości skanów:

• dla kąta [math]270^0[/math] 5, 5,
• dla kąta [math]90^0[/math] 5, 5,

Dokonujemy teraz korekty:

[math] \begin{array}{l} \mu^1(1,1) = \mu^{0}(1,1) + \frac{(P(270,1) - P^0(270,1))}{2} = 2.5 + \frac{3-5}{2} = 1.5 \\ \\ \mu^1(1,2) = \mu^{0}(1,2) + \frac{(P(270,1) - P^0(270,1))}{2} = 2.5 + \frac{3-5}{2} = 1.5 \\ \\ \mu^1(2,1) = \mu^{0}(2,1) + \frac{(P(270,2) - P^0(270,2))}{2} = 2.5 + \frac{7-5}{2} = 3.5 \\ \\ \mu^1(1,2) = \mu^{0}(1,2) + \frac{(P(270,2) - P^0(270,2))}{2} = 2.5 + \frac{7-5}{2} = 3.5 \end{array} [/math]

co daje następujący rozkład liniowego współczynnika osłabienia promieniowania X:

[math] \begin{array}{|c|c|} 1.5 & 1.5 \\ - & - \\ 3.5 & 3.5 \end{array} [/math]

Wykonamy kolejną korektę tym razem korzystając z wartości rzeczywistych projekcji dla kąta 180 stopni:

[math] \begin{array}{l} \mu^2(1,1) = \mu^{1}(1,1) + \frac{(P(180,1) - P^1(180,1))}{2} = 1.5 + \frac{4-5}{2} = 1 \\ \\ \mu^2(1,2) = \mu^{1}(1,2) + \frac{(P(180,1) - P^1(180,1))}{2} = 1.5 + \frac{6-5}{2} = 2 \\ \\ \mu^2(2,1) = \mu^{1}(2,1) + \frac{(P(180,2) - P^1(180,2))}{2} = 3.5 + \frac{4-5}{2} = 4 \\ \\ \mu^2(1,2) = \mu^{1}(1,2) + \frac{(P(180,2) - P^1(180,2))}{2} = 3.5 + \frac{6-5}{2} = 4 \end{array} [/math]

co daje następujący rozkład liniowego współczynnika osłabienia promieniowania X, zgodny z rozkładem tego parametru w badanym obiekcie:

[math] \begin{array}{|c|c|} 1 & 2 \\ - & - \\ 4 & 4\end{array} [/math]

Budowa i zasada działania Tomografu Rentgenowskiego

Zasada działania skanera CT I generacji. Skaner składał się z pojedynczego detektora i lampy rentgenowskiej emitującej skoligowaną wiązkę promienieniowania X. Lampa i detektor wykonywały ruchu translacyjne i rotacyjne. (Rysunek pochodzi ze strony [2] i został udostępnionego przez dr Jacka Rumińskiego, za co autor niniejszych materiałów serdecznie dziękuje).

Zasada działania skanera CT II generacji. W porównaniu z tomografem I generacji zwiększono do kilku liczbę detektorów, co umożliwiło zmniejszenie ruchów translacyjnych lampy. (Rysunek pochodzi ze strony [2] i został udostępnionego przez dr Jacka Rumińskiego, za co autor niniejszych materiałów serdecznie dziękuje).

Zasada działania skanera CT III generacji. W tej generacji Tomografów wyeliminowano całkowicie ruch translacyjny. Detektory (w liczbie kilkuset) zostały umieszczone na łuku pierścienia, obracającego się razem z lampą dookoła pacjenta. (Rysunek pochodzi ze strony [2] i został udostępnionego przez dr Jacka Rumińskiego, za co autor niniejszych materiałów serdecznie dziękuje).

Zasada działania skanera CT IV generacji. W tej generacji skanerów, detektory umieszczone są na stałe na pierścieniu dookoła pacjenta. Ruch obrotowy wykonuje tylko lampa RTG.(Rysunek pochodzi ze strony [2] i został udostępnionego przez dr Jacka Rumińskiego, za co autor niniejszych materiałów serdecznie dziękuje).

Na rysunku zaprezentowano współczesny tomograf rentgenowski. Zdjęcie pochodzi ze stron Wikipedii.

Budowa wewnętrzna współczesnego skanera trzeciej generacji. Znaczenie symboli: T — lampa RTG, X — wachlarzowa wiązka promieni X, D — matryca detektorów.Zdjęcie pochodzi ze stron Wikipedii.

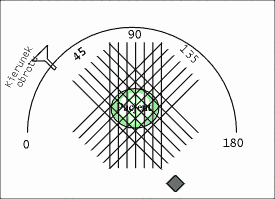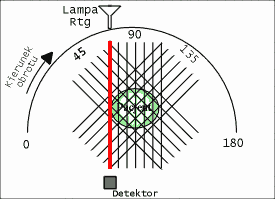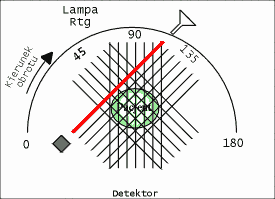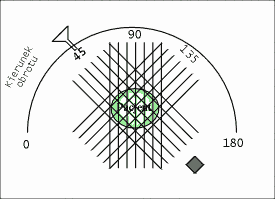
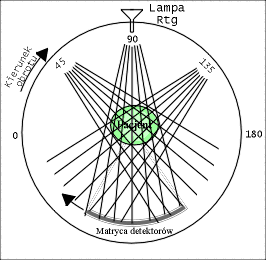
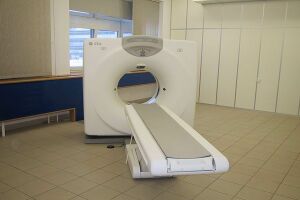
W rozdziale [[2]] dowiedzieliśmy się, iż uzyskanie obrazu wybranego przekroju pacjenta wymaga przeprowadzenia serii naświetleń badanego z różnych kierunków. Wiąże się to oczywiście z ruchem lampy rentgenowskiej i detektorów dookoła pacjenta. W pierwszych Tomografach CT elementy te wykonywały ruchy translacyjne i rotacyjne, opisane w poprzednim rozdziale. Niestety, lampa Rentgenowska jest urządzeniem ciężkim, które ponadto musi być chłodzone za pomocą odpowiedniej cieczy (np. wody lub oleju). Tego rodzaju układ pomiarowy nie może się szybko przesuwać, gdyż ciężka lampa ma pewną bezwładność, co utrudnia jest rozpędzenie i zatrzymania. W efekcie, pierwsze badania diagnostyczne trwały niezmiernie długo, zaś sam sprzęt szybko się zużywał. W kolejnych latach opracowywano nowe rozwiązania, prowadzące do minimalizacji liczby ruchów, takie jak np. zwiększenie ilości detektorów. Rozwiązania te nazwano generacjami Tomografów Rentgenowskich. Do chwili obecnej opracowano IV generacje tomografów, które zaprezentowano na rysunkach: rys. 2, rys. 3, rys. 4, rys. 5. Obecnie w użytku znajdują się tomografy III i IV generacji. Zdjęcie współczesnego tomografu zaprezentowano na rys. 6, natomiast wnętrze tomografu III generacji na rys. 7. W pierwszych tomografach RTG stosowano detektory ksenonowe, które szybko zostały wyparte przez detektory scyntylacyjne (które zostaną omówione w rozdziale dotyczący metody SPECT i PET). Te z kolei są obecnie zastępowane przez detektory półprzewodnikowe. Współczesny zestaw do Rentgenowskiej Tomografii Komputerowej (III i IV generacji) składa się z następujących elementów:

• gantry — główny element urządzenia, w środku którego znajdują się mocowania detektorów i pierścienia, po którym porusza się lampa RTG; na obudowie gantry znajduje się także mały pulpit sterowniczy, który np. umożliwia pochylenie całego urządzenia względem stołu z leżącym pacjentem; wnętrze gantry zaprezentowano na rys. 7,
• stół, na którym układany jest pacjent,
• konsoli operatora, komputera i monitora, znajdujących się w oddzielnym pomieszczeniu zabezpieczonym przed promieniowaniem jonizującym,
• generator wysokiego napięcia dla lampy RTG.

Lampy Rentgenowskie Stosowane w CT

Lampa rentgenowska, ma zazwyczaj wirującą anodę. W porównani udo klasycznego aparatu RTG kolimatory są usytuowane nie tylko w pobliżu lampy rentgenowskiej, lecz także przy każdym z detektorów. Kolimatory wykonane są z ołowiu i kształtują wiązkę promieniowania i minimalizują promieniowanie rozpraszane. Od wysokości kolimatorów zależy grubość skanowanej warstwy (najczęściej od 0.5 do 10 mm). Lampy rentgenowskie stosowane w tomografach komputerowych pracują w warunkach silnego obciążenia mechanicznego. Aby uzyskać jak najbardziej stabilną wiązkę promieniowania stosuje się np. podwójne łożyskowanie wirującej anody. Stabilność wiązki promieniowania zależy również w dużej mierze nie od konstrukcji samej lampy, lecz od stabilności generatora wysokiego napięcia (różnica potencjałów między anodą a katodą) oraz prądu przepływającego przez żarnik katody. Typowe parametry lampy RTG stosowanej w CT to napięcie przyspieszające około 160 kV (zwykle jednak w granicy 80 – 125 kV), prąd anodowy o wartości od 30 do 500 mA.

Detektory promieniowania X stosowane w CT

W pierwszych skanerach CT, w których stosowano pojedyncze detektory promieniowania jonizującego, do rejestracji promieniowania Rentgenowskiego stosowano detektory scyntylacyjne . Obecnie detektory te są wypierane przez detektory półprzewodnikowe, dlatego detektorom scyntylacyjnym w tym miejscu nie będziemy poświęcaj dużo uwagi (dokładnie detektory scyntylacyjne zostaną omówione przy metodzie SPECT i PET, gdzie są niezwykle ważnym elementem aparatury diagnostycznej). Zasada działania detektora scyntylacyjnego jest następująca. Promieniowanie jonizujące powoduje wzbudzenie atomów lub molekuł scyntylatora, które następnie oddają tak uzyskaną energie poprzez emisję promieniowania elektromagnetycznego w zakresie widzialnym. Fotony tego promieniowania zostają następnie zamienione przez fotoprzetwornik (fotopowielacz lub fotodioda) na przepływ prądu elektrycznego. Istotnym elementem detektora scyntylacyjnego jest fotoprzetwornik, czyli układ konwertujący światło powstałe pod wpływem promieniowania na sygnał elektryczny. W czasie powstawania pierwszych tomografów CT, najlepszymi fotoprzetwornikami były fotopowielacze. Detektory scyntylacyjne charakteryzują się wysoką czułością detekcji promieniowania X, jednakże każdy kryształ scyntylacyjny wymagał połączenia z osobną fotopowielaczem, który jest rodzajem lampy elektronowej, o stosunkowo dużych rozmiarach i wymagającym zasilania wysokim napięciem.

W latach 90-tych postęp technologicznych umożliwił konstruowanie tanich, małych i odpowiednio czułych fotodiod krzemowych. Fotodiody to diody półprzewodnikowe, których działanie polega na wykorzystaniu zjawiska fotoelektrycznego zachodzącego w obszarze złącza p-n. Przez fotodiodę, do której przyłożone jest napięcie w kierunku zaporowym, płynie prąd proporcjonalny do wielkości strumienia padającego światła. Zalety fotodiody w porównaniu z fotopowielaczem to przede wszystkim niskie napięcie zasilania oraz mały rozmiar i masa Obecnie kryształy scyntylacyjne zaczęły być wypierane przez detektory półprzewodnikowe cezowe lub kadmowo-wolframowe. Detektory te świeciły pod wpływem promieniowania rentgenowskiego światłem z zakresu widzialnego, które za pomocą fotodetektorów półprzewodnikowych jest zamieniane na sygnał elektryczny.

Wizualizacja zrekonstruowanego obrazu.

W wyniku procesu skanowania pacjenta skolimowaną wiązką promieniowania Rentgenowskiego, możliwa jest uzyskanie rozkładu liniowego współczynnika osłabienia promieniowania X. Uzyskany obraz prezentowany jest jednak w jednostkach względnych nazywanych jednostkami Hounsfielda (Haunsfield Unit, HU) . Najczęściej jako wynik badania tomograficznego podawana jest mapa współczynników osłabienia promieniowania X wyrażona w tzw. jednostkach Haunsfielda (HU – Haunsfield Unit):

[math] HU = 1000\cdot\frac{\mu_{tkanki} - \mu_{wody}}{ \mu_{wody}} [/math]

gdzie:
[math]\mu_{wody}[/math] dla temperatury 20 stopni Celsjusza i energii promieniowania 73 kV Stosowanie takich jednostek ma uzasadnienie praktyczne – lekarz oceniający zdjęcie dokonuje porównania wartości osłabienia promieniowania X w różnych częściach ciała pacjenta. Do celów porównawczych znacznie wygodniejsze są wartości względne niż bezwzględne.

Wartości współczynniki osłabienia wiązki promieniowania X, wytworzonego w lampie rentgenowskiej, pracującej przy napięciu 120kV wyrażone w jednostkach HU:

Tkanka	Wartość HU
Plazma krwi	~22
Skrzep	~74
Obrzęk	~19
Tkanka tłuszczowa	-25 do -200
Tkanka mięśniowa	~67
Wątroba	~71
Trzustka	~64
Kora mózgowa	~36
Powietrze	-1000
Płuca
Tkanka kostna	1000 do 3100
Tkanka zmieniona nowotworowo	od 25 do 90	250-300
Rdzeń kręgowy	1-5	300-500

Najmniejsza różnica HU rejestrowana przez Tomografy Rentgenowskie nie jest specyfikowana przez producentów, jednakże szacuje się ją na poziomie 4 HU.

Uzyskiwane w obrazowaniu CT obrazu cechuje dynamika w jednostkach HU od wartości -1000 do około 3100. Do ich reprezentacji wystarczy zatem 4096 poziomów (12 bitów). Obrazy te prezentowane są w skali szarości, jednakże monochromatyczna skala obejmuje 256 odcieni szarości. Oko rozpoznaje około 50 poziomów szarości. W związku z tym, ogranicza się zakres zmienność danych do celów prezentacyjnych. Proces te nazywa się okienkowaniem. Lekarz wybiera położenie środka (window level, WL) okna na skali HU (np. 100 HU) i szerokość okna (window width, WW), (np. 50 HU) . Na obrazie zostaną zaprezentowane struktury o HU w zakresie od WL – WW/2 do WL + WW/2 (w podanym przykładzie od 75 do 125 HU). Obniżenie poziomu okna umożliwia oglądanie struktur o mniejszym HU. Poszerzenie szerokości okna zmniejsza kontrast obrazu.

Część ciała/narząd	WL (HU)	WW(HU)
Płuca	-700	750
Głowa Dziecka	35	90
Ramię	40	500
Brzuch (okolice wątroby)	40	300
Brzuch (okolice nerek)	40	350
Kręgosłup odcinek lędźwiowy	40	400

Dodatkowe Rozwiązania

Tomografia Helikalna (Spiralna)

W systemach od I do IV generacji wykonanie pomiaru i rekonstrukcji kolejnej warstwy wymagało zatrzymania ruchu obrotowego lampy i przesuniecie stołu z pacjentem.W celu maksymalnego skrócenia czasu wykonywania badania znacznych obszarów ciała ludzkiego, firma Toshiba opracowała technologię w której w trakcie obrotu lampy rentgenowskiej w skanerach III i IV generacji przesuwany jest jednocześnie stół z pacjentem. Wypadkowy ruch lampy rentgenowskiej wokół pacjenta, będący złożeniem translacyjnego ruchu stołu i ruchu obrotowego lampy, odbywa się po torze nazywany helisą. Tego rodzaju technologia umożliwia skrócenie badania dużych obszarów pacjenta z 20 – 30minut do około 10 minut. Firma Toshiba zarezerwowała nazwę Tomografii Helikalnej tylko dla swoich produktów. Konkurencja, podążając za pomysłodawcą nazwała swoje tomografy Tomografami Spiralnymi.

HR CT

High Resolution CT (HR CT) to technika obrazowania płuc mająca na celu uzyskanie jak największej rozdzielczości przestrzennej, celem diagnostyki zmian w śródmiąższu płuc, takich jak zwłóknienia, rozedma, choroby oskrzelików (średnica oskrzelików 1 - 2 mm). W celu polepszenia kontrastu i zobrazowania interesujących struktur można zwiększyć natężenie promieniowania X, kosztem ilości diagnozowanych warstw. W technice HRCT obrazowane są warstwy o grubości od 1 – 2 mm, ale odległości pomiędzy kolejnymi warstwami wynoszą 10 – 30 mm.

Parametry Akwizycji

W poniższej tabeli podano najważniejsze parametry akwizycji wybranych obszarów człowieka.

Część ciała/Organ	Grubość Przekroju (mm)	mAs
Głowa	10	350-400
Dół tylny czaszki	3-5	350-400
Kości czaszki	1-3	400
Szyja	10	250
	5	200
Klatka piersiowa	1 – 3	250
Płuca	1-3	250
Żołądek	10	250-300
	5	250-300
	3	300
Wątroba	250-300
Miednica	10	250-300
Rdzeń kręgowy	1-5	300-500