Obrazowanie:Obrazowanie Medyczne/Obrazowanie Metodą Magnetycznego Rezonansu Jądrowego: Różnice pomiędzy wersjami
(Utworzono nową stronę "<b>Obrazowanie Metodą Magnetycznego Rezonansu Jądrowego</b> ==Kilka uwag na temat Mechaniki Kwantowej, Mechaniki Klasycznej oraz nazewnictwa.== Prawidłową nazwą met...") |
|||
| Linia 11: | Linia 11: | ||
==Spin i moment magnetyczny jądra atomowego== | ==Spin i moment magnetyczny jądra atomowego== | ||
Jądra atomowe zawierające nieparzystą liczbę protonów lub neutronów mają niezerowy własny moment pędu <math>\vec{I}</math> (spin) oraz związany z nim moment magnetyczny. Zgodnie z regułami opisu wielkości wektorowych w mechanice kwantowej, jednocześnie może być obserwowalna tylko długość wektora oraz wartość jednej z jego składowych (tzw. rzut tego wektora na wyróżnioną oś, nazywaną osią kwantowania). W przypadku wektora własnego momentu pędu jądra atomowego jego długość wynosi <ref name="bid3">H.Haken H.Ch.Wolf "Atomy i kwanty"</ref>: | Jądra atomowe zawierające nieparzystą liczbę protonów lub neutronów mają niezerowy własny moment pędu <math>\vec{I}</math> (spin) oraz związany z nim moment magnetyczny. Zgodnie z regułami opisu wielkości wektorowych w mechanice kwantowej, jednocześnie może być obserwowalna tylko długość wektora oraz wartość jednej z jego składowych (tzw. rzut tego wektora na wyróżnioną oś, nazywaną osią kwantowania). W przypadku wektora własnego momentu pędu jądra atomowego jego długość wynosi <ref name="bid3">H.Haken H.Ch.Wolf "Atomy i kwanty"</ref>: | ||
| − | <equation><math> | + | <equation id="1"><math> |
|\vec{I}| = \hbar\sqrt{I\left(I+1\right)} | |\vec{I}| = \hbar\sqrt{I\left(I+1\right)} | ||
</math></equation> | </math></equation> | ||
| Linia 17: | Linia 17: | ||
<math>I</math> oznacza liczbą kwantową o wartości całkowitej lub połówkowej.<br> | <math>I</math> oznacza liczbą kwantową o wartości całkowitej lub połówkowej.<br> | ||
Składowa <math>z</math> momentu pędu wyraża się następującym wzorem <ref name="bid3" />: | Składowa <math>z</math> momentu pędu wyraża się następującym wzorem <ref name="bid3" />: | ||
| − | <equation><math> | + | <equation id="2"><math> |
\begin{array}{lc} | \begin{array}{lc} | ||
I_{z} = m_{I}\hbar, & m_{I} = \{I,I-1,\dots,-I\} | I_{z} = m_{I}\hbar, & m_{I} = \{I,I-1,\dots,-I\} | ||
| Linia 23: | Linia 23: | ||
</math></equation> | </math></equation> | ||
Możliwych jest zatem <math>2I+1</math> orientacji spinu jądra względem wyróżnionego kierunku, odpowiadających możliwym wartościom jądrowej magnetycznej liczby kwantowej <math>m_{I}</math>. W przypadku protonu (jądra atomu wodoru), mamy: | Możliwych jest zatem <math>2I+1</math> orientacji spinu jądra względem wyróżnionego kierunku, odpowiadających możliwym wartościom jądrowej magnetycznej liczby kwantowej <math>m_{I}</math>. W przypadku protonu (jądra atomu wodoru), mamy: | ||
| − | <equation><math> | + | <equation id="3"><math> |
\begin{array}{l} | \begin{array}{l} | ||
I=1/2\\ | I=1/2\\ | ||
| Linia 33: | Linia 33: | ||
</math></equation> | </math></equation> | ||
Moment magnetyczny związany jest ze spinem następującą zależnością: | Moment magnetyczny związany jest ze spinem następującą zależnością: | ||
| − | <equation><math> | + | <equation id="4"><math> |
\vec{\mu}_{I} = \gamma\vec{I} | \vec{\mu}_{I} = \gamma\vec{I} | ||
</math></equation> | </math></equation> | ||
Stała proporcjonalności <math>\gamma</math> to tzw. jądrowy stosunek giromagnetyczny. Również i w przypadku jądrowego momentu magnetycznego można zmierzyć jednocześnie tyko jego długość i rzut na wyróżnioną oś <math>z</math> wynoszący: | Stała proporcjonalności <math>\gamma</math> to tzw. jądrowy stosunek giromagnetyczny. Również i w przypadku jądrowego momentu magnetycznego można zmierzyć jednocześnie tyko jego długość i rzut na wyróżnioną oś <math>z</math> wynoszący: | ||
| − | <equation><math> | + | <equation id="5"><math> |
\left(\vec{\mu}_{I}\right)_{z} = \gamma\vec{I}_{z} | \left(\vec{\mu}_{I}\right)_{z} = \gamma\vec{I}_{z} | ||
</math></equation> | </math></equation> | ||
Na moment magnetyczny umieszczony w polu magnetycznym <math>\vec{B}</math>, działa pewien moment siły, starający się ustawić momentu magnetycznego zgodnie z kierunkiem pola <math>\vec{B}</math>. Energia potencjalna tego oddziaływania wynosi: | Na moment magnetyczny umieszczony w polu magnetycznym <math>\vec{B}</math>, działa pewien moment siły, starający się ustawić momentu magnetycznego zgodnie z kierunkiem pola <math>\vec{B}</math>. Energia potencjalna tego oddziaływania wynosi: | ||
| − | <equation><math> | + | <equation id="6"><math> |
V = -\vec{\mu}\cdot\vec{B} | V = -\vec{\mu}\cdot\vec{B} | ||
</math></equation> | </math></equation> | ||
| Linia 47: | Linia 47: | ||
Rozważmy pole <math>\vec{B}</math>, posiadające tylko składową wzdłuż osi <math>z</math> układu odniesienia, czyli <math>\vec{B} = \left[ 0, 0, B_{z}\right] </math>. | Rozważmy pole <math>\vec{B}</math>, posiadające tylko składową wzdłuż osi <math>z</math> układu odniesienia, czyli <math>\vec{B} = \left[ 0, 0, B_{z}\right] </math>. | ||
W przypadku protonu, posiadającego ładunek dodatni, orientacji momentu pędu zgodnej z kierunkiem pola <math>\vec{B}</math> będzie odpowiadać energia potencjalna: | W przypadku protonu, posiadającego ładunek dodatni, orientacji momentu pędu zgodnej z kierunkiem pola <math>\vec{B}</math> będzie odpowiadać energia potencjalna: | ||
| − | <equation><math> | + | <equation id="7"><math> |
V = -\mu\cdot B_z=-\gamma I_{z}B_z=-\frac{1}{2}\gamma\hbar B_z | V = -\mu\cdot B_z=-\gamma I_{z}B_z=-\frac{1}{2}\gamma\hbar B_z | ||
</math></equation> | </math></equation> | ||
natomiast orientacji antyrównoległej: | natomiast orientacji antyrównoległej: | ||
| − | <equation><math> | + | <equation id="8"><math> |
V = \mu\cdot B_z=-\gamma I_{z}B_z=\frac{1}{2}\gamma\hbar B_z | V = \mu\cdot B_z=-\gamma I_{z}B_z=\frac{1}{2}\gamma\hbar B_z | ||
</math></equation> | </math></equation> | ||
| Linia 62: | Linia 62: | ||
Rozważmy moment magnetyczny znajdujący się w stałym polu magnetycznym o następującej indukcji:<math>\vec{B}_0 =\left[0, 0, B_{0}\right]</math>. | Rozważmy moment magnetyczny znajdujący się w stałym polu magnetycznym o następującej indukcji:<math>\vec{B}_0 =\left[0, 0, B_{0}\right]</math>. | ||
Szybkość zmian momentu pędu ciała (<math>\vec{I}</math>) jest równa momentowi siły (<math>\vec{N}</math>) działającemu na to ciało: | Szybkość zmian momentu pędu ciała (<math>\vec{I}</math>) jest równa momentowi siły (<math>\vec{N}</math>) działającemu na to ciało: | ||
| − | <equation><math> | + | <equation id="9"><math> |
\frac{d\vec{I}}{dt} = \vec{N} | \frac{d\vec{I}}{dt} = \vec{N} | ||
</math></equation> | </math></equation> | ||
Moment magnetyczny, związany z wewnętrznym momentem pędu jądra, wynosi: | Moment magnetyczny, związany z wewnętrznym momentem pędu jądra, wynosi: | ||
| − | <equation><math> | + | <equation id="10"><math> |
\vec{\mu}_{I} = \gamma\vec{I} | \vec{\mu}_{I} = \gamma\vec{I} | ||
</math></equation> | </math></equation> | ||
Po przekształceniu powyższego równania dostajemy: | Po przekształceniu powyższego równania dostajemy: | ||
| − | <equation><math> | + | <equation id="11"><math> |
\vec{I} = \frac{\vec{\mu}_I}{\gamma} | \vec{I} = \frac{\vec{\mu}_I}{\gamma} | ||
</math></equation> | </math></equation> | ||
W polu magnetycznym <math>\vec{B}_0</math> na moment magnetyczny będzie działa moment siły: | W polu magnetycznym <math>\vec{B}_0</math> na moment magnetyczny będzie działa moment siły: | ||
| − | <equation><math> | + | <equation id="12"><math> |
\vec{N} = \vec{\mu}_{I}\times\vec{B}_0 | \vec{N} = \vec{\mu}_{I}\times\vec{B}_0 | ||
</math></equation> | </math></equation> | ||
| Linia 84: | Linia 84: | ||
</math></equation> | </math></equation> | ||
ponieważ: | ponieważ: | ||
| − | <equation><math> | + | <equation id="13"><math> |
\gamma\vec{\mu}\times\vec{B}_0 = \left[\gamma\mu_{y}B_{0},-\gamma\mu_{x}B_{0},0\right] | \gamma\vec{\mu}\times\vec{B}_0 = \left[\gamma\mu_{y}B_{0},-\gamma\mu_{x}B_{0},0\right] | ||
</math></equation> | </math></equation> | ||
| Linia 102: | Linia 102: | ||
Rozwiązanie równania na wielkość składowej ''z'' wektora momentu magnetycznego jest proste i wynosi: | Rozwiązanie równania na wielkość składowej ''z'' wektora momentu magnetycznego jest proste i wynosi: | ||
| − | <equation><math> | + | <equation id="14"><math> |
\mu_{z} = \mu^{0}_{z} = \mathrm{const} | \mu_{z} = \mu^{0}_{z} = \mathrm{const} | ||
</math></equation> | </math></equation> | ||
| Linia 124: | Linia 124: | ||
Widzimy, że składowa ''x'' momentu magnetycznego drga z częstością <math>-\omega_0</math>. Przyczyna pojawienia się znaku "-" w rozwiązaniu została wyjaśniona na <xr id="fig:mri_basic">rys. %i</xr>. Podstawiając równanie (<xr id="eq:MRI_5"/>) do drugiego równania w układzie (<xr id="eq:MRI_2"/>) dostajemy rozwiązanie na wielkość składowej ''y'' momentu magnetycznego: | Widzimy, że składowa ''x'' momentu magnetycznego drga z częstością <math>-\omega_0</math>. Przyczyna pojawienia się znaku "-" w rozwiązaniu została wyjaśniona na <xr id="fig:mri_basic">rys. %i</xr>. Podstawiając równanie (<xr id="eq:MRI_5"/>) do drugiego równania w układzie (<xr id="eq:MRI_2"/>) dostajemy rozwiązanie na wielkość składowej ''y'' momentu magnetycznego: | ||
| − | <equation><math> | + | <equation id="15"><math> |
\mu_x = A\sin(-\omega_0 t + \phi_0) | \mu_x = A\sin(-\omega_0 t + \phi_0) | ||
</math></equation> | </math></equation> | ||
| Linia 149: | Linia 149: | ||
Składowe ''x'' oraz ''y'' momentu magnetycznego można zapisać w wygodniejszy sposób stosują formalizm liczb zespolonych. | Składowe ''x'' oraz ''y'' momentu magnetycznego można zapisać w wygodniejszy sposób stosują formalizm liczb zespolonych. | ||
Pomnóżmy trzecie równanie w układzie (<xr id="eq:MRI_6"/>) przez liczbę <math>i=\sqrt{-1}</math> i dodajmy do drugiego równania w układzie (<xr id="eq:MRI_6"/>): | Pomnóżmy trzecie równanie w układzie (<xr id="eq:MRI_6"/>) przez liczbę <math>i=\sqrt{-1}</math> i dodajmy do drugiego równania w układzie (<xr id="eq:MRI_6"/>): | ||
| − | <equation><math> | + | <equation id="16"><math> |
\begin{array}{l} | \begin{array}{l} | ||
\vec{\mu}_z = \mu^{0}_{z} = \mathrm{const}\cdot\vec{e}_z \\ | \vec{\mu}_z = \mu^{0}_{z} = \mathrm{const}\cdot\vec{e}_z \\ | ||
| Linia 255: | Linia 255: | ||
<br> | <br> | ||
We wzorze (<xr id="eq:MRI_7"/>) skorzystano z własności trygonometrycznych sinusa i cosinusa: | We wzorze (<xr id="eq:MRI_7"/>) skorzystano z własności trygonometrycznych sinusa i cosinusa: | ||
| − | <equation><math> | + | <equation id="17"><math> |
\begin{array}{ccc} | \begin{array}{ccc} | ||
\sin\left( a + b \right) &=& \sin(a) \cos(b) + \cos(a) \sin(b)\\ | \sin\left( a + b \right) &=& \sin(a) \cos(b) + \cos(a) \sin(b)\\ | ||
| Linia 264: | Linia 264: | ||
==Namagnesowanie próbki== | ==Namagnesowanie próbki== | ||
Namagnesowanie, to całkowity moment magnetyczny, przypadający na jednostkę objętości <math>\Delta V</math>: | Namagnesowanie, to całkowity moment magnetyczny, przypadający na jednostkę objętości <math>\Delta V</math>: | ||
| − | <equation><math> | + | <equation id="17"><math> |
\vec{M} = \frac{\sum_{i=1}^{N}\vec{\mu}_i}{\Delta V} | \vec{M} = \frac{\sum_{i=1}^{N}\vec{\mu}_i}{\Delta V} | ||
</math></equation> | </math></equation> | ||
Rozłóżmy wektor namagnesowania na dwie składowe: tzw. podłużną (<math>\vec{M}_L</math>),to jest równoległą do kierunku pola magnetycznego oraz składową poprzeczną (<math>\vec{M}_T</math>), leżącą w płaszczyźnie prostopadłej do kierunku pola magnetycznego: | Rozłóżmy wektor namagnesowania na dwie składowe: tzw. podłużną (<math>\vec{M}_L</math>),to jest równoległą do kierunku pola magnetycznego oraz składową poprzeczną (<math>\vec{M}_T</math>), leżącą w płaszczyźnie prostopadłej do kierunku pola magnetycznego: | ||
| − | <equation><math> | + | <equation id="18"><math> |
\vec{M} = \vec{M}_L + \vec{M}_T | \vec{M} = \vec{M}_L + \vec{M}_T | ||
</math></equation> | </math></equation> | ||
| Linia 274: | Linia 274: | ||
===Ile wynosi namagnesowanie poprzeczne próbki?=== | ===Ile wynosi namagnesowanie poprzeczne próbki?=== | ||
Składową poprzeczną namagnesowania będziemy oznaczali wektorem <math>\vec{M}_T</math>. Załóżmy, że w próbce znajduje się ''N'' takich samych jąder posiadających moment magnetyczny. Momenty te mają losową orientację przestrzeni. W pewnej chwili, zostaje włączone stałe pole magnetyczne. Stałe ''A'' oraz <math>\phi_0</math> dla każdego momentu magnetycznego wyznaczamy na podstawie orientacji momentu magnetycznego w chwili łączenia pola. Dla każdego jądra magnetycznego stała ''A'' wynikająca z warunków początkowych jak to faza początkowa <math>\phi_0</math> jest dowolna. W związku z czym: | Składową poprzeczną namagnesowania będziemy oznaczali wektorem <math>\vec{M}_T</math>. Załóżmy, że w próbce znajduje się ''N'' takich samych jąder posiadających moment magnetyczny. Momenty te mają losową orientację przestrzeni. W pewnej chwili, zostaje włączone stałe pole magnetyczne. Stałe ''A'' oraz <math>\phi_0</math> dla każdego momentu magnetycznego wyznaczamy na podstawie orientacji momentu magnetycznego w chwili łączenia pola. Dla każdego jądra magnetycznego stała ''A'' wynikająca z warunków początkowych jak to faza początkowa <math>\phi_0</math> jest dowolna. W związku z czym: | ||
| − | <equation><math> | + | <equation id="19"><math> |
\vec{M}_T = \frac{\sum_{i=1}^{N}\vec{\mu}_{T} \cdot \vec{e}_T }{\Delta V} = \frac{\sum_{i=1}^{N}A_i e^{-\omega_0 t + \phi_{0_i}} \cdot \vec{e}_T}{\Delta V} = 0 | \vec{M}_T = \frac{\sum_{i=1}^{N}\vec{\mu}_{T} \cdot \vec{e}_T }{\Delta V} = \frac{\sum_{i=1}^{N}A_i e^{-\omega_0 t + \phi_{0_i}} \cdot \vec{e}_T}{\Delta V} = 0 | ||
</math></equation> | </math></equation> | ||
| Linia 281: | Linia 281: | ||
===Ile wynosi namagnesowanie próbki, czyli namagnesowanie podłużne?=== | ===Ile wynosi namagnesowanie próbki, czyli namagnesowanie podłużne?=== | ||
Przypominamy, że rozważamy cząstkę lub jądro atomowe, znajdujące się w zewnętrznym polu magnetycznym <math>\vec{B}_{0}</math>, skierowanym równolegle do osi <math>z</math>. Składowa <math>z</math> tego pola wynosi <math>B_{0}</math>. W celu uproszczenia problemu przyjmujemy, że cząstka lub jądro atomowe posiada spin równy <math>\frac{1}{2}</math> (np. proton). Moment magnetyczny cząstki lub jądra atomowego może ustawić się zgodnie lub przeciwnie do kierunku zewnętrznego pola magnetycznego. W szczególności składowa <math>z</math> momentu magnetycznego, przyjmie kierunek równoległy bądź antyrównoległy do pola <math>B_{0}</math>, skierowanego wzdłuż osi <math>z</math>. Jak wiemy, układy fizyczne dążą do osiągnięcia stanu, w którym uzyskają minimum energii. Energia potencjalna momentu magnetycznego w zewnętrznym polem magnetycznym wynosi: | Przypominamy, że rozważamy cząstkę lub jądro atomowe, znajdujące się w zewnętrznym polu magnetycznym <math>\vec{B}_{0}</math>, skierowanym równolegle do osi <math>z</math>. Składowa <math>z</math> tego pola wynosi <math>B_{0}</math>. W celu uproszczenia problemu przyjmujemy, że cząstka lub jądro atomowe posiada spin równy <math>\frac{1}{2}</math> (np. proton). Moment magnetyczny cząstki lub jądra atomowego może ustawić się zgodnie lub przeciwnie do kierunku zewnętrznego pola magnetycznego. W szczególności składowa <math>z</math> momentu magnetycznego, przyjmie kierunek równoległy bądź antyrównoległy do pola <math>B_{0}</math>, skierowanego wzdłuż osi <math>z</math>. Jak wiemy, układy fizyczne dążą do osiągnięcia stanu, w którym uzyskają minimum energii. Energia potencjalna momentu magnetycznego w zewnętrznym polem magnetycznym wynosi: | ||
| − | <equation><math> | + | <equation id="20"><math> |
V = -\vec{\mu}\vec{B} | V = -\vec{\mu}\vec{B} | ||
</math></equation> | </math></equation> | ||
Rozwijając powyższy wzór dla rozważanego przez nas przypadku, otrzymujemy: | Rozwijając powyższy wzór dla rozważanego przez nas przypadku, otrzymujemy: | ||
| − | <equation><math> | + | <equation id="21"><math> |
V = -u_{z}B_{0} = -\gamma(\vec{I})_{z}B_{0}=-\gamma\hbar m_{I}B_{0} | V = -u_{z}B_{0} = -\gamma(\vec{I})_{z}B_{0}=-\gamma\hbar m_{I}B_{0} | ||
</math></equation> | </math></equation> | ||
| Linia 291: | Linia 291: | ||
<math>m_{I}=\pm\frac{1}{2}</math><br> | <math>m_{I}=\pm\frac{1}{2}</math><br> | ||
Rzutowi momentu magnetycznego równoległemu do osi <math>z</math>, czyli dla <math>m_{I}=\frac{1}{2}</math>, odpowiada energia potencjalna: | Rzutowi momentu magnetycznego równoległemu do osi <math>z</math>, czyli dla <math>m_{I}=\frac{1}{2}</math>, odpowiada energia potencjalna: | ||
| − | <equation><math> | + | <equation id="22"><math> |
V = -\gamma\frac{\hbar}{2}B_{0} | V = -\gamma\frac{\hbar}{2}B_{0} | ||
</math></equation> | </math></equation> | ||
natomiast rzutowi antyrównoległemu: | natomiast rzutowi antyrównoległemu: | ||
| − | <equation><math> | + | <equation id="23"><math> |
V = \gamma\frac{\hbar}{2}B_{0} | V = \gamma\frac{\hbar}{2}B_{0} | ||
</math></equation> | </math></equation> | ||
| Linia 308: | Linia 308: | ||
<math>N_{\pm}</math> — liczba cząstek o spinie skierowanym odpowiednio równolegle i antyrównolegle do pola <math>B_{0}</math>.<br> | <math>N_{\pm}</math> — liczba cząstek o spinie skierowanym odpowiednio równolegle i antyrównolegle do pola <math>B_{0}</math>.<br> | ||
Podstawiając do wzoru (<xr id="eq:rozB"/>) wyznaczone wcześniej energie potencjalne, odpowiadające dwóm różnym orientacjom spinu w polu <math>B_{0}</math> dostajemy:<br> | Podstawiając do wzoru (<xr id="eq:rozB"/>) wyznaczone wcześniej energie potencjalne, odpowiadające dwóm różnym orientacjom spinu w polu <math>B_{0}</math> dostajemy:<br> | ||
| − | <equation><math> | + | <equation id="24"><math> |
\frac{N_{+}}{N_{-}} = \frac{e^{-\frac{-\frac{\hbar}{2}\gamma B_{0}}{k_{b}T}}}{e^{-\frac{\frac{\hbar}{2}\gamma B_{0}}{k_{b}T}}}=e^{\frac{\gamma\hbar B_{0}}{k_{b}T}} | \frac{N_{+}}{N_{-}} = \frac{e^{-\frac{-\frac{\hbar}{2}\gamma B_{0}}{k_{b}T}}}{e^{-\frac{\frac{\hbar}{2}\gamma B_{0}}{k_{b}T}}}=e^{\frac{\gamma\hbar B_{0}}{k_{b}T}} | ||
</math></equation> | </math></equation> | ||
W temperaturze pokojowej, różnice obsadzeń poszczególnych poziomów energetycznych są nieznaczne, dlatego skorzystamy z przybliżenia: | W temperaturze pokojowej, różnice obsadzeń poszczególnych poziomów energetycznych są nieznaczne, dlatego skorzystamy z przybliżenia: | ||
| − | <equation><math> | + | <equation id="25"><math> |
e^{\frac{\gamma\hbar B_{0}}{k_{b}T}}\approx 1+ \frac{\gamma\hbar B_{0}}{k_{b}T} | e^{\frac{\gamma\hbar B_{0}}{k_{b}T}}\approx 1+ \frac{\gamma\hbar B_{0}}{k_{b}T} | ||
</math></equation> | </math></equation> | ||
Różnica w ilości obsadzeń poszczególnych poziomów energetycznych jest zatem równa: | Różnica w ilości obsadzeń poszczególnych poziomów energetycznych jest zatem równa: | ||
| − | <equation><math> | + | <equation id="26"><math> |
\Delta N = N_{+} - N_{-} = \frac{\gamma\hbar B_{0}}{k_{b}T}N_{-}\approx\frac{\gamma\hbar B_{0}}{k_{b}T}\frac{1}{2}N_{t} | \Delta N = N_{+} - N_{-} = \frac{\gamma\hbar B_{0}}{k_{b}T}N_{-}\approx\frac{\gamma\hbar B_{0}}{k_{b}T}\frac{1}{2}N_{t} | ||
</math></equation> | </math></equation> | ||
| Linia 322: | Linia 322: | ||
<math>N_{t}</math> to liczba wszystkie jąder atomu wodoru w badanej próbce.<br> | <math>N_{t}</math> to liczba wszystkie jąder atomu wodoru w badanej próbce.<br> | ||
Czynnik <math>\frac{\gamma\hbar B_{0}}{k_{b}T}</math> w temperaturze ciała ludzkiego <math>T=310K</math> i polu magnetycznym <math>B_{0}=1T</math> jest równy: | Czynnik <math>\frac{\gamma\hbar B_{0}}{k_{b}T}</math> w temperaturze ciała ludzkiego <math>T=310K</math> i polu magnetycznym <math>B_{0}=1T</math> jest równy: | ||
| − | <equation><math> | + | <equation id="27"><math> |
\frac{\gamma\hbar B_{0}}{k_{b}T}\approx 7\cdot10^{-6} | \frac{\gamma\hbar B_{0}}{k_{b}T}\approx 7\cdot10^{-6} | ||
</math></equation> | </math></equation> | ||
Wynik ten oznacza, że na każdy milion protonów o spinie skierowanym przeciwnie do pola magnetycznego, przypada milion plus siedem protonów o spinie skierowanym równolegle do pola i ta niewielka nadwyżka protonów w stanie o korzystniejszej energii jest odpowiedzialna za namagnesowanie próbki. Wartość nadwyżki wydaje się być niezwykle mała. Należy jednak pamiętać, że ilość protonów jaka występuje w organizmie ludzkim jest niezmiernie duża, co umożliwia rejestrację wytworzonego namagnesowania. Jeden gram wody zawiera <math>\frac{1}{8}</math> mola atomów wodoru. W jednym molu materii występuje <math>6.023\cdot10^{32}</math> cząsteczek, a zatem gram wody zawiera <math>N_{t} = 6.68\cdot10^{22}</math> atomów wodoru. Nadwyżka <math>\Delta N</math> wynosi zatem <math>\Delta N\approx 2.2\cdot10^{17}</math> protonów. | Wynik ten oznacza, że na każdy milion protonów o spinie skierowanym przeciwnie do pola magnetycznego, przypada milion plus siedem protonów o spinie skierowanym równolegle do pola i ta niewielka nadwyżka protonów w stanie o korzystniejszej energii jest odpowiedzialna za namagnesowanie próbki. Wartość nadwyżki wydaje się być niezwykle mała. Należy jednak pamiętać, że ilość protonów jaka występuje w organizmie ludzkim jest niezmiernie duża, co umożliwia rejestrację wytworzonego namagnesowania. Jeden gram wody zawiera <math>\frac{1}{8}</math> mola atomów wodoru. W jednym molu materii występuje <math>6.023\cdot10^{32}</math> cząsteczek, a zatem gram wody zawiera <math>N_{t} = 6.68\cdot10^{22}</math> atomów wodoru. Nadwyżka <math>\Delta N</math> wynosi zatem <math>\Delta N\approx 2.2\cdot10^{17}</math> protonów. | ||
Całkowity podłużny moment magnetyczny wytworzony przez 1 gram wody wynosi: | Całkowity podłużny moment magnetyczny wytworzony przez 1 gram wody wynosi: | ||
| − | <equation><math> | + | <equation id="28"><math> |
\left|\mu_{L}\right| = \Delta N\left<\mu_{z}\right>=\Delta N \frac{1}{2}\hbar\gamma = \Delta n\cdot 1.4\cdot10^{-26}\textrm{J/T} = 3.1\cdot10^{-9}\textrm{Am}^{2} | \left|\mu_{L}\right| = \Delta N\left<\mu_{z}\right>=\Delta N \frac{1}{2}\hbar\gamma = \Delta n\cdot 1.4\cdot10^{-26}\textrm{J/T} = 3.1\cdot10^{-9}\textrm{Am}^{2} | ||
</math></equation> | </math></equation> | ||
Z kolei namagnesowanie to całkowity moment magnetyczny na jednostkę objętości. Jeden gram wody zajmuje objętość <math>10^{-6}\mathrm m^{-3}</math> | Z kolei namagnesowanie to całkowity moment magnetyczny na jednostkę objętości. Jeden gram wody zajmuje objętość <math>10^{-6}\mathrm m^{-3}</math> | ||
a zatem namagnesowanie wytworzone 2 jednym gramie wody w polu magnetycznym o wartości indukcji <math>B_{0}=1</math>T w temperaturze <math>T=310</math>K wyniesie: | a zatem namagnesowanie wytworzone 2 jednym gramie wody w polu magnetycznym o wartości indukcji <math>B_{0}=1</math>T w temperaturze <math>T=310</math>K wyniesie: | ||
| − | <equation><math> | + | <equation id="29"><math> |
\left|M\right|=3.1\cdot10^{-3}\textrm{A/m} | \left|M\right|=3.1\cdot10^{-3}\textrm{A/m} | ||
</math></equation> | </math></equation> | ||
| Linia 350: | Linia 350: | ||
Indukcja zmiennego pola magnetycznego <math>\vec{B}_1</math> jest rzędu <math>10^{-5}</math> T, a zatem jest znacznie mniejsza od indukcji statycznego pola magnetycznego <math>\vec{B}</math>. Pole <math>\vec{B}_1</math> nazywane jest impulsem pobudzającym (ang. ''Radio Frequency'', RF), włączane jest bowiem na krótki okres czasu (co wyjaśnimy dalej). Impuls RF wytwarza się za pomocą cewek w postaci fali elektromagnetycznej. | Indukcja zmiennego pola magnetycznego <math>\vec{B}_1</math> jest rzędu <math>10^{-5}</math> T, a zatem jest znacznie mniejsza od indukcji statycznego pola magnetycznego <math>\vec{B}</math>. Pole <math>\vec{B}_1</math> nazywane jest impulsem pobudzającym (ang. ''Radio Frequency'', RF), włączane jest bowiem na krótki okres czasu (co wyjaśnimy dalej). Impuls RF wytwarza się za pomocą cewek w postaci fali elektromagnetycznej. | ||
Okazuje się, że pole opisane wzorem (<xr id="eq:MRI_7"/>) możemy rozłożyć na dwa pola, rotujące w płaszczyźnie ''x-y'' w przeciwne strony: | Okazuje się, że pole opisane wzorem (<xr id="eq:MRI_7"/>) możemy rozłożyć na dwa pola, rotujące w płaszczyźnie ''x-y'' w przeciwne strony: | ||
| − | <equation><math> | + | <equation id="29"><math> |
\begin{array}{l} | \begin{array}{l} | ||
\vec{B}_{1_R}\left(t\right) = \left[B_{1}\cos\left(-\omega_1 t\right),B_{1}\sin\left(-\omega_1 t\right),0\right] | \vec{B}_{1_R}\left(t\right) = \left[B_{1}\cos\left(-\omega_1 t\right),B_{1}\sin\left(-\omega_1 t\right),0\right] | ||
| Linia 364: | Linia 364: | ||
Wprowadźmy dwa układy współrzędnych: Układ Laboratoryjny ''U'' oraz układ ''U' '' obracający się z częstością zmiennego pola magnetycznego (<math>\omega_1</math>). Osie ''z'' oraz ''z' '' odpowiednio układu ''U'' oraz ''U' '' są do siebie równoległe. Stałe pole magnetyczne jest skierowane wzdłuż tych osi. Zapiszmy równanie (<xr id="eq:MRI_9"/>) w układzie ''U ' ''. | Wprowadźmy dwa układy współrzędnych: Układ Laboratoryjny ''U'' oraz układ ''U' '' obracający się z częstością zmiennego pola magnetycznego (<math>\omega_1</math>). Osie ''z'' oraz ''z' '' odpowiednio układu ''U'' oraz ''U' '' są do siebie równoległe. Stałe pole magnetyczne jest skierowane wzdłuż tych osi. Zapiszmy równanie (<xr id="eq:MRI_9"/>) w układzie ''U ' ''. | ||
Zgodnie z zasadami transformacji wektorów pomiędzy różnymi układami współrzędnych, równanie (<xr id="eq:MRI_9"/>) w układzie ''U' ''będzie miało postać: | Zgodnie z zasadami transformacji wektorów pomiędzy różnymi układami współrzędnych, równanie (<xr id="eq:MRI_9"/>) w układzie ''U' ''będzie miało postać: | ||
| − | <equation><math> | + | <equation id="a1"><math> |
\left[\frac{d\vec{M}}{dt}\right]_{U'}=\vec{M}\times\left[\left(-\omega_1 + \gamma B_{0}\right)\vec{e}_z + \gamma B_{1}\vec{e}_x\right] | \left[\frac{d\vec{M}}{dt}\right]_{U'}=\vec{M}\times\left[\left(-\omega_1 + \gamma B_{0}\right)\vec{e}_z + \gamma B_{1}\vec{e}_x\right] | ||
</math></equation> | </math></equation> | ||
| Linia 388: | Linia 388: | ||
: <math>\vec{B}_{eff} = B_1\vec{e}_x</math>, <br><br> | : <math>\vec{B}_{eff} = B_1\vec{e}_x</math>, <br><br> | ||
: co oznacza, że wektor namagnesowania zaczyna wykonywać ruch precesyjny wokół pola magnetycznego <math>B_1\vec{e}_x</math>. Ponownie : przypominamy, że <math>B_1<<B_0</math>. Jak widać, przy pomocy pola magnetycznego o niewielkiej indukcji, lecz odpowiednio dobranej częstości, możliwa jest zmiana orientacji wektora namagnesowania. Jest to zjawisko '''Magnetycznego Rezonansu Jądrowego'''. Występowanie w nazwie zjawiska termin ''rezonans'' (kojarzony najczęściej z obwodami elektrycznymi), jest jak najbardziej uzasadnione, ponieważ za pomocą niewielkiego zaburzenia o periodycznym charakterze (ale odpowiednio dobranej częstości), doprowadziliśmy do znaczących zmian w układzie. Częstość ruchu precesyjnego wektora namagnesowania wokół pola <math>\vec{B}_1</math> wynosi: | : co oznacza, że wektor namagnesowania zaczyna wykonywać ruch precesyjny wokół pola magnetycznego <math>B_1\vec{e}_x</math>. Ponownie : przypominamy, że <math>B_1<<B_0</math>. Jak widać, przy pomocy pola magnetycznego o niewielkiej indukcji, lecz odpowiednio dobranej częstości, możliwa jest zmiana orientacji wektora namagnesowania. Jest to zjawisko '''Magnetycznego Rezonansu Jądrowego'''. Występowanie w nazwie zjawiska termin ''rezonans'' (kojarzony najczęściej z obwodami elektrycznymi), jest jak najbardziej uzasadnione, ponieważ za pomocą niewielkiego zaburzenia o periodycznym charakterze (ale odpowiednio dobranej częstości), doprowadziliśmy do znaczących zmian w układzie. Częstość ruchu precesyjnego wektora namagnesowania wokół pola <math>\vec{B}_1</math> wynosi: | ||
| − | <equation><math> | + | <equation id="30"><math> |
\Omega = \gamma B_1 | \Omega = \gamma B_1 | ||
</math></equation> | </math></equation> | ||
: Częstość <math>\Omega</math> jest nazywana częstością Rabbiego. W trakcie czasu <math>\tau></math> namagnesowanie zakreśli kąt <math>\Theta</math> równy: | : Częstość <math>\Omega</math> jest nazywana częstością Rabbiego. W trakcie czasu <math>\tau></math> namagnesowanie zakreśli kąt <math>\Theta</math> równy: | ||
| − | <equation><math> | + | <equation id="1b"><math> |
\Theta = \Omega\tau | \Theta = \Omega\tau | ||
</math></equation> | </math></equation> | ||
| Linia 408: | Linia 408: | ||
===Typowe wartości częstości Larmour'a oraz częstości Rabbiego=== | ===Typowe wartości częstości Larmour'a oraz częstości Rabbiego=== | ||
Opisując zmiany wielkości fizycznych w czasie niejednokrotnie posługujemy się częstością wyrażaną w Hz. W takim przypadku wzór: (<xr id="eq:larmour_kolowa"/>) przyjmie nastepującą postać: | Opisując zmiany wielkości fizycznych w czasie niejednokrotnie posługujemy się częstością wyrażaną w Hz. W takim przypadku wzór: (<xr id="eq:larmour_kolowa"/>) przyjmie nastepującą postać: | ||
| − | <equation><math> | + | <equation id="31"><math> |
f = \frac{\gamma}{2\pi}B_0 | f = \frac{\gamma}{2\pi}B_0 | ||
</math></equation> | </math></equation> | ||
| Linia 452: | Linia 452: | ||
</figure> | </figure> | ||
Jak można zauważyć, największą wartością momentu magnetycznego charakteryzują się jądra atomu wodoru, czyli protony. Częstość precesji Larmour'a dla protonów umieszczonych w polu magnetycznym o indukcji <math>B_0=1</math> T osiągnie wielkość: | Jak można zauważyć, największą wartością momentu magnetycznego charakteryzują się jądra atomu wodoru, czyli protony. Częstość precesji Larmour'a dla protonów umieszczonych w polu magnetycznym o indukcji <math>B_0=1</math> T osiągnie wielkość: | ||
| − | <equation><math> | + | <equation id="32"><math> |
f_0 = \frac{\gamma}{2\pi} B_0 = 42,58 \left[\frac{\textrm{MHz}}{T}\right] \cdot \textrm{[T]} = 42,58 \textrm{MHz} | f_0 = \frac{\gamma}{2\pi} B_0 = 42,58 \left[\frac{\textrm{MHz}}{T}\right] \cdot \textrm{[T]} = 42,58 \textrm{MHz} | ||
</math></equation> | </math></equation> | ||
Dodatkowe, zmienne pola magnetyczne <math>\vec{B}_1</math>, stosowane do zmiany orientacji wektora namagnesowania, mają niewielkie wartości, rzędu <math>10^{-5}</math>T. | Dodatkowe, zmienne pola magnetyczne <math>\vec{B}_1</math>, stosowane do zmiany orientacji wektora namagnesowania, mają niewielkie wartości, rzędu <math>10^{-5}</math>T. | ||
Po wprowadzeniu próbki zawierającej jądra atomu wodoru w dodatkowe pole magnetyczne <math>\vec{B}_1</math>, wirujące w płaszczyźnie prostopadłej do kierunku pola statycznego, namagnesowanie zaczyna wykonywać obrót w płaszczyźnie równoległej do kierunku pola statycznego z częstością Rabbiego równą: | Po wprowadzeniu próbki zawierającej jądra atomu wodoru w dodatkowe pole magnetyczne <math>\vec{B}_1</math>, wirujące w płaszczyźnie prostopadłej do kierunku pola statycznego, namagnesowanie zaczyna wykonywać obrót w płaszczyźnie równoległej do kierunku pola statycznego z częstością Rabbiego równą: | ||
| − | <equation><math> | + | <equation id="33"><math> |
f_1 = \frac{\gamma}{2\pi} B_1 = 42,58 \left[\frac{\textrm{MHz}}{T}\right] \cdot 10^{-3} \textrm{[T]} = 0.0580 \textrm{MHz} | f_1 = \frac{\gamma}{2\pi} B_1 = 42,58 \left[\frac{\textrm{MHz}}{T}\right] \cdot 10^{-3} \textrm{[T]} = 0.0580 \textrm{MHz} | ||
</math></equation> | </math></equation> | ||
| Linia 463: | Linia 463: | ||
===Impulsy <math>\pi</math> oraz <math>\frac{\pi}{2}</math>=== | ===Impulsy <math>\pi</math> oraz <math>\frac{\pi}{2}</math>=== | ||
Jak dowiedzieliśmy się w poprzednich rozdziałach, przy pomocy rotującego pola magnetycznego o odpowiednio dobranej częstości, możemy zmienić orientacje wektora namagnesowania. Jest to o tyle ważne, iż wektor ten wywołuje pole magnetyczne dużo mniejsze z w porównaniu do wartości pola statycznego <math>\vec{B}_0</math>, do którego jest równoległy. Uniemożliwia to pomiar wartości magnetyzacji próbki. Zmianę orientacji wektora namagnesowania określa się za pomocą kąta, o jaki odchyla się on od kierunku statycznego pola magnetycznego <math>\vec{B}_0</math>, które leży wzdłuż osi ''Z'' przyjętego przez nas układu współrzędnych. Kąt ten można wyliczyć za pomocą wzoru na częstość Rabbiego. Jeśli wektor namagnesowania w trakcie rezonansu wykonuje precesję wokół pola <math>B_1</math> z częstością: | Jak dowiedzieliśmy się w poprzednich rozdziałach, przy pomocy rotującego pola magnetycznego o odpowiednio dobranej częstości, możemy zmienić orientacje wektora namagnesowania. Jest to o tyle ważne, iż wektor ten wywołuje pole magnetyczne dużo mniejsze z w porównaniu do wartości pola statycznego <math>\vec{B}_0</math>, do którego jest równoległy. Uniemożliwia to pomiar wartości magnetyzacji próbki. Zmianę orientacji wektora namagnesowania określa się za pomocą kąta, o jaki odchyla się on od kierunku statycznego pola magnetycznego <math>\vec{B}_0</math>, które leży wzdłuż osi ''Z'' przyjętego przez nas układu współrzędnych. Kąt ten można wyliczyć za pomocą wzoru na częstość Rabbiego. Jeśli wektor namagnesowania w trakcie rezonansu wykonuje precesję wokół pola <math>B_1</math> z częstością: | ||
| − | <equation><math> | + | <equation id="33"><math> |
\Omega = \gamma B_1 | \Omega = \gamma B_1 | ||
</math></equation> | </math></equation> | ||
to w czasie τ zakreśli on kąt: | to w czasie τ zakreśli on kąt: | ||
| − | <equation><math> | + | <equation id="34"><math> |
\Theta = \Omega\cdot\tau = \gamma B_1\tau | \Theta = \Omega\cdot\tau = \gamma B_1\tau | ||
</math></equation> | </math></equation> | ||
| Linia 488: | Linia 488: | ||
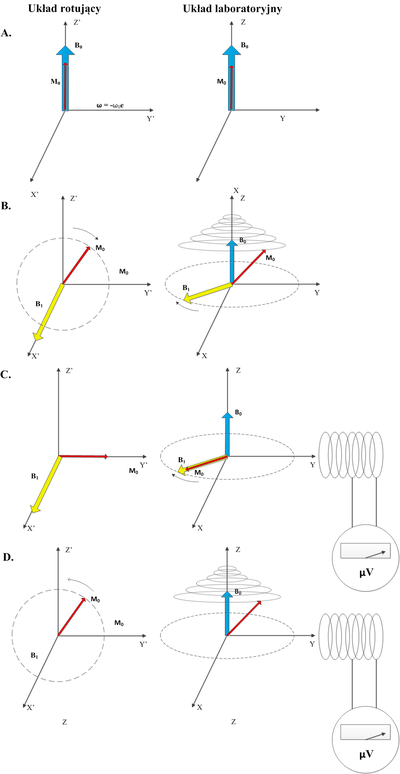
Poruszyliśmy również kwestie doboru czasu impulsu rotującego pola magnetycznego, tak aby zmienić orientację wektora namagnesowania o kąt <math>\pi</math> lub <math>\frac{\pi}{2}</math>. Po obróceniu magnetyzacji o wymagany kąt, impulsowe pole magnetyczne jest wyłączane i dokonywany jest pomiar namagnesowania próbki. Co dalej dzieje się z wektorem magnetyzacji ? Obrót wektora namagnesowania jest niczym innym jak wytrąceniem układu z położenia równowagi termodynamicznej. Jak pamiętamy z pierwszych rozdziałów dotyczących MRI, momenty magnetyczne jąder atomowych starają ustawić się w kierunku pola magnetycznego. Układ będzie zatem dążył do powrotu do stanu równowagi. Przypominamy, iż wyróżniliśmy dwie składowe namagnesowania: namagnesowanie podłużne (<math>\vec{M}_L</math> oraz namagnesowanie poprzeczne <math>\vec{M}_T</math>. Przyjmijmy, że umieszczenie próbki w polu magnetycznym wywołuje namagnesowanie o wartości <math>M_0</math> i rozważmy składowe namagnesowania w układzie rotującym ''U' '' w następujących przypadkach: | Poruszyliśmy również kwestie doboru czasu impulsu rotującego pola magnetycznego, tak aby zmienić orientację wektora namagnesowania o kąt <math>\pi</math> lub <math>\frac{\pi}{2}</math>. Po obróceniu magnetyzacji o wymagany kąt, impulsowe pole magnetyczne jest wyłączane i dokonywany jest pomiar namagnesowania próbki. Co dalej dzieje się z wektorem magnetyzacji ? Obrót wektora namagnesowania jest niczym innym jak wytrąceniem układu z położenia równowagi termodynamicznej. Jak pamiętamy z pierwszych rozdziałów dotyczących MRI, momenty magnetyczne jąder atomowych starają ustawić się w kierunku pola magnetycznego. Układ będzie zatem dążył do powrotu do stanu równowagi. Przypominamy, iż wyróżniliśmy dwie składowe namagnesowania: namagnesowanie podłużne (<math>\vec{M}_L</math> oraz namagnesowanie poprzeczne <math>\vec{M}_T</math>. Przyjmijmy, że umieszczenie próbki w polu magnetycznym wywołuje namagnesowanie o wartości <math>M_0</math> i rozważmy składowe namagnesowania w układzie rotującym ''U' '' w następujących przypadkach: | ||
1.Włączone pole statyczne, wtedy:<br> | 1.Włączone pole statyczne, wtedy:<br> | ||
| − | <equation><math> | + | <equation id="35"><math> |
\vec{M} = | \vec{M} = | ||
\left[\begin{array}{l} | \left[\begin{array}{l} | ||
| Linia 504: | Linia 504: | ||
</math></equation> <br> | </math></equation> <br> | ||
2. Zadziałanie na próbkę impulsem <math>\frac{\pi}{2}</math>, po którym magnetyzacja wynosi: | 2. Zadziałanie na próbkę impulsem <math>\frac{\pi}{2}</math>, po którym magnetyzacja wynosi: | ||
| − | <equation><math> | + | <equation id="36"><math> |
\vec{M} = | \vec{M} = | ||
\left[\begin{array}{l} | \left[\begin{array}{l} | ||
| Linia 541: | Linia 541: | ||
W półklasycznego równaniu (<xr id="eq:rownaie_ruchu_w_wirujacym_ukladzie_odniesienia"/>) opisującym zachowanie się namagnesowania w polu magnetycznym musimy uwzględnić procesy związane z relaksacją spinów. | W półklasycznego równaniu (<xr id="eq:rownaie_ruchu_w_wirujacym_ukladzie_odniesienia"/>) opisującym zachowanie się namagnesowania w polu magnetycznym musimy uwzględnić procesy związane z relaksacją spinów. | ||
Bloch wprowadził fenomenologiczne poprawki do tego równania opierając się na rozumowaniu, które można wyrazić następującymi równaniami: | Bloch wprowadził fenomenologiczne poprawki do tego równania opierając się na rozumowaniu, które można wyrazić następującymi równaniami: | ||
| − | <equation><math> | + | <equation id="37"><math> |
\begin{array}{l} | \begin{array}{l} | ||
\frac{dM_{x}}{dt} = -\frac{M_{x}}{T_{2}}\\ | \frac{dM_{x}}{dt} = -\frac{M_{x}}{T_{2}}\\ | ||
| Linia 561: | Linia 561: | ||
Proste równanie opisujące zachowanie się momentów magnetycznych oraz magnetyzacji, które wyprowadziliśmy analogicznie jak się to czyni w przypadku ruchu bąka symetrycznego w polu grawitacyjnym nie jest pełne i powinno być rozszerzone o procesy relaksacji. Fenomenologiczne, klasyczne równanie opisującym zachowanie się namagnesowania w polu magnetycznym z uwzględnieniem procesów relaksacji nazywamy równaniem Blocha: | Proste równanie opisujące zachowanie się momentów magnetycznych oraz magnetyzacji, które wyprowadziliśmy analogicznie jak się to czyni w przypadku ruchu bąka symetrycznego w polu grawitacyjnym nie jest pełne i powinno być rozszerzone o procesy relaksacji. Fenomenologiczne, klasyczne równanie opisującym zachowanie się namagnesowania w polu magnetycznym z uwzględnieniem procesów relaksacji nazywamy równaniem Blocha: | ||
| − | <equation><math> | + | <equation id="38"><math> |
\left[\frac{d\vec{M}}{dt}\right]_{U'} = \gamma\vec{M}\times\vec{B}_{eff} - \left(M_{x}\vec{e}_{x} + M_{y}\vec{e}_{y}\right)/T_{2} - \left(M_{z}-M_{0}\vec{e}_{z}\right)/T_{1} | \left[\frac{d\vec{M}}{dt}\right]_{U'} = \gamma\vec{M}\times\vec{B}_{eff} - \left(M_{x}\vec{e}_{x} + M_{y}\vec{e}_{y}\right)/T_{2} - \left(M_{z}-M_{0}\vec{e}_{z}\right)/T_{1} | ||
</math></equation> | </math></equation> | ||
| Linia 594: | Linia 594: | ||
</math></equation> | </math></equation> | ||
Rozwiązanie w układzie laboratoryjnym uzyskamy, po przemnożeniu równania (<xr id="eq:bloch_rozw_1"/>) przez macierz obrotu <math>P</math>: | Rozwiązanie w układzie laboratoryjnym uzyskamy, po przemnożeniu równania (<xr id="eq:bloch_rozw_1"/>) przez macierz obrotu <math>P</math>: | ||
| − | <equation><math> | + | <equation id="39"><math> |
\vec{M} = P\times [\vec{M}]_{rot} | \vec{M} = P\times [\vec{M}]_{rot} | ||
</math></equation> | </math></equation> | ||
| Linia 609: | Linia 609: | ||
<br> | <br> | ||
co prowadzi to ostatecznie do wyniku: | co prowadzi to ostatecznie do wyniku: | ||
| − | <equation><math> | + | <equation id="40"><math> |
\vec{M} = P\cdot[\vec{M}]_{rot} \rightarrow \vec{M} = \left[\begin{array}{l} | \vec{M} = P\cdot[\vec{M}]_{rot} \rightarrow \vec{M} = \left[\begin{array}{l} | ||
0\\ | 0\\ | ||
| Linia 635: | Linia 635: | ||
</math></equation> | </math></equation> | ||
przy następujących warunkach początkowych: | przy następujących warunkach początkowych: | ||
| − | <equation><math> | + | <equation id="41"><math> |
\vec{M} = P\cdot[\vec{M}]_{rot} \rightarrow \vec{M} = \left[\begin{array}{l} | \vec{M} = P\cdot[\vec{M}]_{rot} \rightarrow \vec{M} = \left[\begin{array}{l} | ||
0\\ | 0\\ | ||
| Linia 656: | Linia 656: | ||
gdzie: <math>\Omega = \gamma B_1</math>. | gdzie: <math>\Omega = \gamma B_1</math>. | ||
Rozwiązanie w układzie laboratoryjnym uzyskamy, po przemnożeniu równania (<xr id="eq:bloch_rozw_2"/>) przez macierz obrotu <math>P</math>: | Rozwiązanie w układzie laboratoryjnym uzyskamy, po przemnożeniu równania (<xr id="eq:bloch_rozw_2"/>) przez macierz obrotu <math>P</math>: | ||
| − | <equation><math> | + | <equation id="42"><math> |
\vec{M} = P\cdot[\vec{M}]_{rot} | \vec{M} = P\cdot[\vec{M}]_{rot} | ||
</math></equation> | </math></equation> | ||
co prowadzi do następującego równania na ewolucję magnetyzacji w układzie laboratoryjnym: | co prowadzi do następującego równania na ewolucję magnetyzacji w układzie laboratoryjnym: | ||
Rozwiązanie układu równań (<xr id="eq:bloch_2"/>) ma postać: | Rozwiązanie układu równań (<xr id="eq:bloch_2"/>) ma postać: | ||
| − | <equation><math> | + | <equation id="43"><math> |
\begin{array}{l} | \begin{array}{l} | ||
M_x = M_0\sin(\Omega t)\sin(\omega_0 t)\\ | M_x = M_0\sin(\Omega t)\sin(\omega_0 t)\\ | ||
| Linia 690: | Linia 690: | ||
</math></equation> | </math></equation> | ||
przy warunkach początkowych | przy warunkach początkowych | ||
| − | <equation><math> | + | <equation id="44"><math> |
\vec{M} = P\cdot[\vec{M}]_{rot} \rightarrow \vec{M} = \left[\begin{array}{l} | \vec{M} = P\cdot[\vec{M}]_{rot} \rightarrow \vec{M} = \left[\begin{array}{l} | ||
0\\ | 0\\ | ||
| Linia 760: | Linia 760: | ||
Czasy relaksacji zależą od właściwości fizyko-chemicznych tkanek. Stanowią zatem niezwykle cenna informację dla diagnostyki medycznej. Relaksacja spin-sieć zależy głównie od czynników "''naturalnych''" — fluktuacji lokalnych pół magnetycznych wytworzonych przez otoczenie jąder atomowych. Relaksacja spin-spin zależy zarówno od czynników naturalnych jak i "''sztucznych''" — niejednorodności statycznego pola magnetycznego związanych np. z ograniczoną dokładnością wykonania skanera MRI. | Czasy relaksacji zależą od właściwości fizyko-chemicznych tkanek. Stanowią zatem niezwykle cenna informację dla diagnostyki medycznej. Relaksacja spin-sieć zależy głównie od czynników "''naturalnych''" — fluktuacji lokalnych pół magnetycznych wytworzonych przez otoczenie jąder atomowych. Relaksacja spin-spin zależy zarówno od czynników naturalnych jak i "''sztucznych''" — niejednorodności statycznego pola magnetycznego związanych np. z ograniczoną dokładnością wykonania skanera MRI. | ||
W efekcie, zamiast obserwować zanik namagnesowania poprzecznego z czasem <math>T_{2}</math>, obserwujemy ten zanik z czasem: | W efekcie, zamiast obserwować zanik namagnesowania poprzecznego z czasem <math>T_{2}</math>, obserwujemy ten zanik z czasem: | ||
| − | <equation><math> | + | <equation id="45"><math> |
\frac{1}{T^{*}_{2}} = \frac{1}{T_{2}} + \frac{\gamma\Delta B_{0}}{2} | \frac{1}{T^{*}_{2}} = \frac{1}{T_{2}} + \frac{\gamma\Delta B_{0}}{2} | ||
</math></equation> | </math></equation> | ||
| Linia 776: | Linia 776: | ||
W jaki sposób jednak za pomocą MRI można otrzymać obraz, np. wnętrza ciała ludzkiego? Dotychczas zdobyta przez nas wiedza umożliwia nam pomiar magnetyzacji wytworzonej w badanej próbce, jednak nie potrafimy określić współrzędnych pewnej objętości materii, gdzie to namagnesowanie zostało wytworzone. Jak wiemy z poprzednich rozdziałów, namagnesowanie to wypadkowy moment magnetyczny pewnej objętości materii, który nazywamy wokselem. Cewka rejestruje zbiorczy sygnał pochodzący od wielu wokseli. W chwili wyłączenia impulsu pobudzającego <math>\frac{\pi}{2}</math>, ewolucję wektora namagnesowania opisuje następujący wzór: | W jaki sposób jednak za pomocą MRI można otrzymać obraz, np. wnętrza ciała ludzkiego? Dotychczas zdobyta przez nas wiedza umożliwia nam pomiar magnetyzacji wytworzonej w badanej próbce, jednak nie potrafimy określić współrzędnych pewnej objętości materii, gdzie to namagnesowanie zostało wytworzone. Jak wiemy z poprzednich rozdziałów, namagnesowanie to wypadkowy moment magnetyczny pewnej objętości materii, który nazywamy wokselem. Cewka rejestruje zbiorczy sygnał pochodzący od wielu wokseli. W chwili wyłączenia impulsu pobudzającego <math>\frac{\pi}{2}</math>, ewolucję wektora namagnesowania opisuje następujący wzór: | ||
| − | <equation><math> | + | <equation id="46"><math> |
dS\left(t\right) = AM^{0}\left(\vec{r}\right)e^{-i\left(w_{0}t\right)}e^{-\frac{t}{T_{2}}}dxdydz | dS\left(t\right) = AM^{0}\left(\vec{r}\right)e^{-i\left(w_{0}t\right)}e^{-\frac{t}{T_{2}}}dxdydz | ||
</math></equation> | </math></equation> | ||
gdzie: <math>A</math> jest pewną stałą zależną od geometrii cewek, zaś <math>M^{0}(\vec{r})</math> jest namagnesowaniem woksela, o objętości <math>dx\cdot dy\cdot dz</math>, którego pozycja jest opisana wektorem <math>\vec{r} = [x,y,z]</math> w kartezjańskim układzie współrzędnych. | gdzie: <math>A</math> jest pewną stałą zależną od geometrii cewek, zaś <math>M^{0}(\vec{r})</math> jest namagnesowaniem woksela, o objętości <math>dx\cdot dy\cdot dz</math>, którego pozycja jest opisana wektorem <math>\vec{r} = [x,y,z]</math> w kartezjańskim układzie współrzędnych. | ||
Zbiorczy sygnał rejestrowany przez cewkę odbiorczą wynosi z objętości <math>V</math>: | Zbiorczy sygnał rejestrowany przez cewkę odbiorczą wynosi z objętości <math>V</math>: | ||
| − | <equation><math> | + | <equation id="47"><math> |
S\left(t\right) = A\int\int_{V}\int M^{0}\left(\vec{r}\right)e^{-i\left(\gamma B_{0}t\right)}e^{-\frac{t}{T_{2}}}dxdydz | S\left(t\right) = A\int\int_{V}\int M^{0}\left(\vec{r}\right)e^{-i\left(\gamma B_{0}t\right)}e^{-\frac{t}{T_{2}}}dxdydz | ||
</math></equation> | </math></equation> | ||
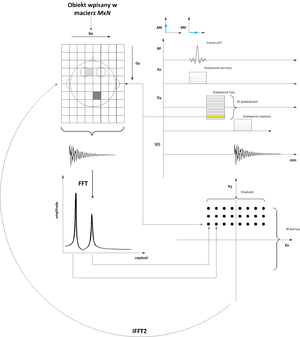
| − | Rozwiązanie tego problemu podali niezależnie Paul Lauterbur <ref name="Lauterbur">P. C. Lauterbur. Image formation by induced local interactions: examples employing nuclear magnetic resonance. Nature 242, 190-191 (1973)</ref> oraz Peter Mansfield <ref name="Mansifeld">P. Mansfield, P.K. Grannell, J. Phys. C: Solid State Phys. 6, L422 (1973)</ref>. W roku 2003 obydwaj naukowcy zostali uhonorowani nagrodą Nobla w dziedzinie medycyny za wykorzystanie Magnetycznego Rezonansu Jądrowego w tej dziedzinie. W roku 1972 Paul Lauterbur przeprowadził doświadczenie, w którym wykazał, że przy wykorzystaniu gradientu dodatkowego pola magnetycznego możliwe jest rozróżnienie rejestrowanych sygnałów przez cewki, pochodzących od dwóch różnych próbek z wodą. | + | Rozwiązanie tego problemu podali niezależnie Paul Lauterbur <ref name="Lauterbur">P. C. Lauterbur. Image formation by induced local interactions: examples employing nuclear magnetic resonance. Nature 242, 190-191 (1973)</ref> oraz Peter Mansfield <ref name="Mansifeld">P. Mansfield, P.K. Grannell, J. Phys. C: Solid State Phys. 6, L422 (1973)</ref>. W roku 2003 obydwaj naukowcy zostali uhonorowani nagrodą Nobla w dziedzinie medycyny za wykorzystanie Magnetycznego Rezonansu Jądrowego w tej dziedzinie. W roku 1972 Paul Lauterbur przeprowadził doświadczenie, w którym wykazał, że przy wykorzystaniu gradientu dodatkowego pola magnetycznego możliwe jest rozróżnienie rejestrowanych sygnałów przez cewki, pochodzących od dwóch różnych próbek z wodą. Ideę eksperymentu zaprezentowano na <xr d="fig:Lauterbur_eksperyment_1">rys. %i</xr> i <xr id="fig:Lauterbur_eksperyment_2">rys. %i</xr>. Jak widzimy, w celu określenia pozycji woksela, z którego mierzony jest dany sygnał FID niezbędne jest wprowadzenie dodatkowego, gradientowego pola magnetycznego: |
| − | <equation><math> | + | <equation id="48"><math> |
\vec{B} = B_0\vec{e}_z + \vec{G}\cdot\vec{r} | \vec{B} = B_0\vec{e}_z + \vec{G}\cdot\vec{r} | ||
</math></equation> | </math></equation> | ||
| Linia 791: | Linia 791: | ||
<math>\vec{G} = [G_x,G_y,G_z]</math> - gradient indukcji pola magnetycznego. | <math>\vec{G} = [G_x,G_y,G_z]</math> - gradient indukcji pola magnetycznego. | ||
W zależności od położenia woksela, częstość precesji momentów magnetycznych w zmodyfikowanym polu będzie wynosić: | W zależności od położenia woksela, częstość precesji momentów magnetycznych w zmodyfikowanym polu będzie wynosić: | ||
| − | <equation><math> | + | <equation id="49"><math> |
\omega(x,y,z) = \gamma \left(B_0 + G_x\cdot x + G_y\cdot y + G_z\cdot z\right) | \omega(x,y,z) = \gamma \left(B_0 + G_x\cdot x + G_y\cdot y + G_z\cdot z\right) | ||
</math></equation> | </math></equation> | ||
| Linia 811: | Linia 811: | ||
*<math>G_{zz}</math> — gradient pola magnetycznego, nałożony na pole <math>B_{0}</math>, <math>G_{zz} = \frac{\Delta B_{0}}{\Delta z}</math>. | *<math>G_{zz}</math> — gradient pola magnetycznego, nałożony na pole <math>B_{0}</math>, <math>G_{zz} = \frac{\Delta B_{0}}{\Delta z}</math>. | ||
Naświetlając badany obiekt polem elektromagnetycznym o częstości <math>\omega_{RF}</math>, wzbudzimy jądra atomowe w tych wokselach, w których spełniony jest warunek rezonansowy (<math>\omega_{RF} = \omega_{0}</math>), czyli w wokselach, których współrzędna <math>z</math> wyraża się wzorem (<xr id="kodowanie_z"/>). Opisana powyżej procedurę rzeczywiście stosuje się w MRI i określa jako etap wyboru warstwy (''Slice selection''), a gradient <math>G_{zz}</math> '''{gradientem wyboru warstwy'''. Grubość wybranej w trakcie badania warstwy wynosi: | Naświetlając badany obiekt polem elektromagnetycznym o częstości <math>\omega_{RF}</math>, wzbudzimy jądra atomowe w tych wokselach, w których spełniony jest warunek rezonansowy (<math>\omega_{RF} = \omega_{0}</math>), czyli w wokselach, których współrzędna <math>z</math> wyraża się wzorem (<xr id="kodowanie_z"/>). Opisana powyżej procedurę rzeczywiście stosuje się w MRI i określa jako etap wyboru warstwy (''Slice selection''), a gradient <math>G_{zz}</math> '''{gradientem wyboru warstwy'''. Grubość wybranej w trakcie badania warstwy wynosi: | ||
| − | <equation><math> | + | <equation id="49"><math> |
\Delta z = \frac{\Delta \omega}{\gamma G_{zz}} | \Delta z = \frac{\Delta \omega}{\gamma G_{zz}} | ||
</math></equation> | </math></equation> | ||
| Linia 825: | Linia 825: | ||
Natychmiast po wyłączeniu pola gradientowego <math>G_{zz}</math> włączane jest pole gradientowe <math>G_{yz}</math> — tzw. '''gradient kodowania fazy''', wzdłuż osi <math>y</math>. Częstość precesji po włączeniu tego pola wynosi: | Natychmiast po wyłączeniu pola gradientowego <math>G_{zz}</math> włączane jest pole gradientowe <math>G_{yz}</math> — tzw. '''gradient kodowania fazy''', wzdłuż osi <math>y</math>. Częstość precesji po włączeniu tego pola wynosi: | ||
| − | <equation><math> | + | <equation id="50"><math> |
\omega_{0} = \gamma\left(B_{0} + G_{yz}y\right) | \omega_{0} = \gamma\left(B_{0} + G_{yz}y\right) | ||
</math></equation> | </math></equation> | ||
| Linia 834: | Linia 834: | ||
</math></equation> | </math></equation> | ||
Rozdzielczość obrazu tomograficznego wzdłuż osi <math>y</math> wynosi: | Rozdzielczość obrazu tomograficznego wzdłuż osi <math>y</math> wynosi: | ||
| − | <equation><math> | + | <equation id="51"><math> |
\Delta y = \frac{\pi}{\gamma G_{yz}T_{y}} | \Delta y = \frac{\pi}{\gamma G_{yz}T_{y}} | ||
</math></equation> | </math></equation> | ||
| Linia 866: | Linia 866: | ||
</math> | </math> | ||
Mierzony sygnał rezonansowy pochodzący od danego woksela w płaszczyźnie <math>x-y</math> można wyrazić w następujący sposób: | Mierzony sygnał rezonansowy pochodzący od danego woksela w płaszczyźnie <math>x-y</math> można wyrazić w następujący sposób: | ||
| − | <equation><math> | + | <equation id="52"><math> |
dS\left(t\right) = AM^{0}(\vec{r})e^{-i\left(w_{0}\left(x\right)t + \phi\left(y\right)\right)}e^{-\frac{t}{T_{2}}}dxdydz | dS\left(t\right) = AM^{0}(\vec{r})e^{-i\left(w_{0}\left(x\right)t + \phi\left(y\right)\right)}e^{-\frac{t}{T_{2}}}dxdydz | ||
</math></equation> | </math></equation> | ||
Będziemy w dalej zajmowali się problemem wyznaczenia rozkładu gęstości protonów w płaszczyźnie już wybranej warstwy o grubości <math>dz</math>, dlatego wprowadzimy stałą <math>B = A\cdot dz</math>. | Będziemy w dalej zajmowali się problemem wyznaczenia rozkładu gęstości protonów w płaszczyźnie już wybranej warstwy o grubości <math>dz</math>, dlatego wprowadzimy stałą <math>B = A\cdot dz</math>. | ||
| − | <equation><math> | + | <equation id="53"><math> |
dS\left(t\right) = BM^{0}(\vec{r})e^{-i\left(w_{0}\left(x\right)t + \phi\left(y\right)\right)}e^{-\frac{t}{T_{2}}}dxdy | dS\left(t\right) = BM^{0}(\vec{r})e^{-i\left(w_{0}\left(x\right)t + \phi\left(y\right)\right)}e^{-\frac{t}{T_{2}}}dxdy | ||
</math></equation> | </math></equation> | ||
gdzie <math>B</math> jest pewną stałą zależną od grubości warstwy oraz geometrii cewek, zaś <math>M^{0}(\vec{r})</math> jest początkowym namagnesowaniem poprzecznym, uzyskanym w wyniku pobudzenia jąder atomowych impulsem <math>RF</math>. | gdzie <math>B</math> jest pewną stałą zależną od grubości warstwy oraz geometrii cewek, zaś <math>M^{0}(\vec{r})</math> jest początkowym namagnesowaniem poprzecznym, uzyskanym w wyniku pobudzenia jąder atomowych impulsem <math>RF</math>. | ||
Podstawiając do powyższego równania wzory (<xr id="eq:kodowanie_fazy"/>) i (<xr id="eq:kodowanie_czestosci"/>) otrzymujemy: | Podstawiając do powyższego równania wzory (<xr id="eq:kodowanie_fazy"/>) i (<xr id="eq:kodowanie_czestosci"/>) otrzymujemy: | ||
| − | <equation><math> | + | <equation id="54"><math> |
dS\left(t\right) = BM^{0}(\vec{r})e^{-i\left(\gamma\left(B_{0} + G_{xz}x\right)t + \gamma G_{yz}yT_{y}\right)}e^{-\frac{t}{T_{2}}}dxdy | dS\left(t\right) = BM^{0}(\vec{r})e^{-i\left(\gamma\left(B_{0} + G_{xz}x\right)t + \gamma G_{yz}yT_{y}\right)}e^{-\frac{t}{T_{2}}}dxdy | ||
</math></equation> | </math></equation> | ||
a zatem sygnał rezonansowy rejestrowany z całej warstwy o współrzędnej <math>z</math> wynosi: | a zatem sygnał rezonansowy rejestrowany z całej warstwy o współrzędnej <math>z</math> wynosi: | ||
| − | <equation><math> | + | <equation id="55"><math> |
S\left(t\right) = B\int\int M^{0}(\vec{r})e^{-i\left(\gamma\left(B_{0} + G_{xz}x\right)t + \gamma G_{yz}yT_{y}\right)}e^{-\frac{t}{T_{2}}}dxdy | S\left(t\right) = B\int\int M^{0}(\vec{r})e^{-i\left(\gamma\left(B_{0} + G_{xz}x\right)t + \gamma G_{yz}yT_{y}\right)}e^{-\frac{t}{T_{2}}}dxdy | ||
</math></equation> | </math></equation> | ||
Otrzymane równanie porządkujemy w następujący sposób: | Otrzymane równanie porządkujemy w następujący sposób: | ||
| − | <equation><math> | + | <equation id="55"><math> |
S\left(t\right) = Be^{-\frac{t}{T_{2}}}\int\int M^{0}(\vec{r})e^{-i\left(\gamma\left(B_{0} + G_{xz}x\right)t + \gamma G_{yz}yT_{y}\right)}dxdy | S\left(t\right) = Be^{-\frac{t}{T_{2}}}\int\int M^{0}(\vec{r})e^{-i\left(\gamma\left(B_{0} + G_{xz}x\right)t + \gamma G_{yz}yT_{y}\right)}dxdy | ||
</math></equation> | </math></equation> | ||
| − | <equation><math> | + | <equation id="56"><math> |
S\left(t\right) = Be^{-\frac{\gamma B_{0}t}{T_{2}}}\int\int M^{0}(\vec{r})e^{-i\left(\gamma G_{xz}xt + \gamma G_{yz}yT_{y}\right)}dxdy | S\left(t\right) = Be^{-\frac{\gamma B_{0}t}{T_{2}}}\int\int M^{0}(\vec{r})e^{-i\left(\gamma G_{xz}xt + \gamma G_{yz}yT_{y}\right)}dxdy | ||
</math></equation> | </math></equation> | ||
podstawiając: | podstawiając: | ||
| − | <equation><math> | + | <equation id="57"><math> |
\begin{array}{l} | \begin{array}{l} | ||
k_{x} = \gamma G_{xz}t\\ | k_{x} = \gamma G_{xz}t\\ | ||
| Linia 902: | Linia 902: | ||
</math></equation> | </math></equation> | ||
Wymiar stałej <math>B</math> zawiera jednostkę długości (powiązaną z grubością warstwy), z kolei namagnesowanie to całkowity moment magnetyczny przypadający na jednostkę objętości <math>dV</math>. Namagnesowanie woksela zależeć będzie od całkowitej liczby jąder atomowych znajdujących się w objętości <math>dV</math>. W związku z tym, uwzględniając jednostkę stałej <math>B</math> oraz namagnesowania <math>M^{0}</math> możemy przepisać równanie (<xr id="eq:mierzony_sygnal"/>) do następującej postaci: | Wymiar stałej <math>B</math> zawiera jednostkę długości (powiązaną z grubością warstwy), z kolei namagnesowanie to całkowity moment magnetyczny przypadający na jednostkę objętości <math>dV</math>. Namagnesowanie woksela zależeć będzie od całkowitej liczby jąder atomowych znajdujących się w objętości <math>dV</math>. W związku z tym, uwzględniając jednostkę stałej <math>B</math> oraz namagnesowania <math>M^{0}</math> możemy przepisać równanie (<xr id="eq:mierzony_sygnal"/>) do następującej postaci: | ||
| − | <equation><math> | + | <equation id="58"><math> |
S\left(k_{x},k_{y}\right) = B'e^{-\frac{\gamma B_{0}t}{T_{2}}}\int\int \rho^{0}_{xy}e^{-i\left(k_{x}x + k_{y}y\right)}dxdy | S\left(k_{x},k_{y}\right) = B'e^{-\frac{\gamma B_{0}t}{T_{2}}}\int\int \rho^{0}_{xy}e^{-i\left(k_{x}x + k_{y}y\right)}dxdy | ||
</math></equation> | </math></equation> | ||
gdzie <math>B'</math> to stała zależna już tylko od właściwości cewek, natomiast <math>\rho^{0}_{xy}</math> jest gęstością jąder atomowych w badanej warstwie. Widzimy zatem, iż mierzony sygnał jest transformatą Fouriera gęstości jąder atomowych, z dokładnością do wagi, zależnej od natężenia statycznego pola magnetycznego oraz czasu relaksacji <math>T_{2}</math><ref>Należy również pamiętać, iż wyznaczona gęstość jąder atomowych (w praktyce jąder atomu wodoru) zależy również od czasu powtarzania wzbudzeń jąder atomowych (''Time Repetition —TR'') oraz czasu echa spinowego (''Time Echo — TE'')</ref>. | gdzie <math>B'</math> to stała zależna już tylko od właściwości cewek, natomiast <math>\rho^{0}_{xy}</math> jest gęstością jąder atomowych w badanej warstwie. Widzimy zatem, iż mierzony sygnał jest transformatą Fouriera gęstości jąder atomowych, z dokładnością do wagi, zależnej od natężenia statycznego pola magnetycznego oraz czasu relaksacji <math>T_{2}</math><ref>Należy również pamiętać, iż wyznaczona gęstość jąder atomowych (w praktyce jąder atomu wodoru) zależy również od czasu powtarzania wzbudzeń jąder atomowych (''Time Repetition —TR'') oraz czasu echa spinowego (''Time Echo — TE'')</ref>. | ||
Rozkład gęstości jąder atomowych można wyznaczyć obliczając odwrotną transformatę Fouriera równania (<xr id="eq:mierzony_sygnal"/>) | Rozkład gęstości jąder atomowych można wyznaczyć obliczając odwrotną transformatę Fouriera równania (<xr id="eq:mierzony_sygnal"/>) | ||
| − | <equation><math> | + | <equation id="59"><math> |
\rho^{0}_{xy} = B'e^{-\frac{\gamma B_{0}t}{T_{2}}}\int\int S\left(k_{x},k_{y}\right)e^{i\left(k_{x}x + k_{y}y\right)}dk_{x}dk_{y} | \rho^{0}_{xy} = B'e^{-\frac{\gamma B_{0}t}{T_{2}}}\int\int S\left(k_{x},k_{y}\right)e^{i\left(k_{x}x + k_{y}y\right)}dk_{x}dk_{y} | ||
</math></equation> | </math></equation> | ||
| Linia 983: | Linia 983: | ||
Podstawowy opis kwantowy zjawiska rezonansu magnetycznego przeprowadzimy dla protonu. Przypominamy, własny moment pędu protonu opisywany jest spinową liczbą kwantową <math>I = \frac{1}{2}</math>, długość wektora momentu pędu wynosi <math>|\vec{I}| = \frac{\sqrt{3}}{2}\hbar </math>, zaś rzut wektora spinu na oś ''Z'' może przyjmować wartości: <math>\vec{I}_{z} = \pm\frac{1}{2}\hbar </math>. Pod nieobecność zewnętrznego pola magnetycznego, rzutom wektora spinu proton una oś ''Z'' odpowiadają stany o tej samej energii. <br> | Podstawowy opis kwantowy zjawiska rezonansu magnetycznego przeprowadzimy dla protonu. Przypominamy, własny moment pędu protonu opisywany jest spinową liczbą kwantową <math>I = \frac{1}{2}</math>, długość wektora momentu pędu wynosi <math>|\vec{I}| = \frac{\sqrt{3}}{2}\hbar </math>, zaś rzut wektora spinu na oś ''Z'' może przyjmować wartości: <math>\vec{I}_{z} = \pm\frac{1}{2}\hbar </math>. Pod nieobecność zewnętrznego pola magnetycznego, rzutom wektora spinu proton una oś ''Z'' odpowiadają stany o tej samej energii. <br> | ||
Wprowadzenie próbki w stałe pola magnetyczne o wartości <math>B_0</math> i kierunku równoległego do osi ''X'' powoduje rozczepienie tych stanów. Rzut wektora momentu magnetycznego (związanego ze spinem) na oś ''Z'' może mieć kierunek równoległy lub przeciwny do kierunku pola magnetycznego. Rzutom tym odpowiadają dwa poziomy energetyczne: | Wprowadzenie próbki w stałe pola magnetyczne o wartości <math>B_0</math> i kierunku równoległego do osi ''X'' powoduje rozczepienie tych stanów. Rzut wektora momentu magnetycznego (związanego ze spinem) na oś ''Z'' może mieć kierunek równoległy lub przeciwny do kierunku pola magnetycznego. Rzutom tym odpowiadają dwa poziomy energetyczne: | ||
| − | <equation><math> | + | <equation id="60"><math> |
\begin{array}{l} | \begin{array}{l} | ||
E_1 = -\frac{1}{2}\hbar\gamma B_0\\ | E_1 = -\frac{1}{2}\hbar\gamma B_0\\ | ||
| Linia 991: | Linia 991: | ||
</math></equation> | </math></equation> | ||
gdzie: <math>E_1, E_2</math> to odpowiednio energia stanu związanego z równoległym i przeciwnym rzutem momentu magnetycznego na kierunek stałego pola magnetycznego. Zgodnie z zasadami termodynamiki, protony będą dążyły do zajmowania stanów o niższej energii. Dostarczając dodatkową energię, np. za pomocą fali elektromagnetycznej, można doprowadzić do przejścia protonów ze stanu podstawowego do wzbudzonego. Częstość fali elektromagnetycznej można wyliczyć w następujący sposób. Różnica energii pomiędzy dwoma stanami wynosi: | gdzie: <math>E_1, E_2</math> to odpowiednio energia stanu związanego z równoległym i przeciwnym rzutem momentu magnetycznego na kierunek stałego pola magnetycznego. Zgodnie z zasadami termodynamiki, protony będą dążyły do zajmowania stanów o niższej energii. Dostarczając dodatkową energię, np. za pomocą fali elektromagnetycznej, można doprowadzić do przejścia protonów ze stanu podstawowego do wzbudzonego. Częstość fali elektromagnetycznej można wyliczyć w następujący sposób. Różnica energii pomiędzy dwoma stanami wynosi: | ||
| − | <equation><math> | + | <equation id="61"><math> |
\Delta E = E_2 - E_1 = \hbar \gamma B_0 | \Delta E = E_2 - E_1 = \hbar \gamma B_0 | ||
</math></equation> | </math></equation> | ||
Fala elektromagnetyczna o częstości <math>\omega_0</math> posiada energię: | Fala elektromagnetyczna o częstości <math>\omega_0</math> posiada energię: | ||
| − | <equation><math> | + | <equation id="62"><math> |
E = \hbar \omega_0 | E = \hbar \omega_0 | ||
</math></equation> | </math></equation> | ||
Energia fali elektromagnetycznej powinna być równa różnicy energii dwóch stanów kwantowych: | Energia fali elektromagnetycznej powinna być równa różnicy energii dwóch stanów kwantowych: | ||
| − | <equation><math> | + | <equation id="63"><math> |
\Delta E = \hbar \omega_0 \rightarrow \hbar \gamma B_0 = \hbar \omega_0 | \Delta E = \hbar \omega_0 \rightarrow \hbar \gamma B_0 = \hbar \omega_0 | ||
</math></equation> | </math></equation> | ||
ostatecznie, częstość fali wzbudzającej przejścia pomiędzy poziomami energetycznymi jest równa: | ostatecznie, częstość fali wzbudzającej przejścia pomiędzy poziomami energetycznymi jest równa: | ||
| − | <equation><math> | + | <equation id="64"><math> |
\omega_0 = \gamma B_0 | \omega_0 = \gamma B_0 | ||
</math></equation> | </math></equation> | ||
Wersja z 21:08, 31 paź 2015
Obrazowanie Metodą Magnetycznego Rezonansu Jądrowego
Spis treści
- 1 Kilka uwag na temat Mechaniki Kwantowej, Mechaniki Klasycznej oraz nazewnictwa.
- 2 Spin
- 3 Spin i moment magnetyczny jądra atomowego
- 4 Moment magnetyczny w stałym zewnętrznym polu magnetycznym
- 5 Namagnesowanie próbki
- 6 Zmiana orientacji wektora namagnesowania. Magnetyczny Rezonans Jądrowy
- 7 Procesy Relaksacji
- 8 Równanie Blocha
- 9 Kodowanie Obrazu
- 10 Etap kodowania częstości i odczyt pomiaru magnetyzacji
- 11 Dekodowanie obrazu
- 12 Podstawowa Sekwencja Gradientów Pola Magnetycznego
- 13 Co obrazuje Magnetyczny Rezonans Jądrowy
- 14 Budowa skanera MRI
- 15 Podstawy kwantowego opisu zjawiska Rezonansu Magnetycznego
- 16 Kwantowy opis zjawiska Rezonansu Magnetycznego
- 17 Spin
- 18 Terminy stosowane w diagnostyce MRI
Kilka uwag na temat Mechaniki Kwantowej, Mechaniki Klasycznej oraz nazewnictwa.
Prawidłową nazwą metody diagnostyki medycznej, która będzie omawiana w tej części skryptu, jest Obrazowanie Magnetycznego Rezonansu Jądrowego (ang. Nuclear Magnetic Rezonanse Imaging, NMRI). Niestety, większość społeczeństwa negatywnie kojarzy przymiotnik jądrowy. W związku z tym, pomimo iż diagnostyka NMRI nie ma nic wspólnego ze zjawiskiem rozpadu promieniotwórczego i jest uznawana za całkowicie bezpieczną, usunięto z jej nazwy słowo "jądrowy" (nuclear). Obecnie metodę NMRI określa się jako ’’Magnetic Rezonanse Imaging – MRI", czyli Obrazowanie Rezonansu Magnetycznego. W żargonie stosowanym w niektórych placówkach medycznych nazwa ta uległa skróceniu do jednego wyrazu — Rezonans. Metoda NMRI opiera się na zjawisku Magnetycznego Rezonansu Jądrowego które omówimy na gruncie Mechaniki Klasycznej z elementami Mechaniki Kwantowej. Zastosowanie modelu kwantowego prowadzi do pełniejszego w porównaniu z modelem klasycznym opisu zjawiska NMR, jednak ze względu na skomplikowaną postać samej Teorii Kwantów, model kwantowy może być trudny w zrozumieniu. Z kolei model klasyczno-kwantowy (nazywany również modelem pół-klasycznym), jest łatwiejszy do przyswojenia i dla pewnej klasy problemów uzyskuje się za jego pomocą te same wyniki co w modelu kwantowym.
Spin
Dokładny opis spinu, który jest wielkością kwantową, wykracza znacznie poza ramy materiału niniejszego skryptu. W tym miejscu natomiast ograniczymy się do podania kilku faktów, obserwacji, czy uwag, mając nadzieję, że wystarczą one czytelnikom do zrozumienia, czym jest spin, przynajmniej w takim stopniu, który ułatwi im przyswojenie wiadomości na temat Jądrowego Rezonansu Magnetycznego. Podstawowymi elementami, z których składa się materia, są cząstki takie jak elektron, proton oraz neutron, które posiadają spin równy [math]\frac{1}{2}[/math]. Najbardziej rozpowszechnionym pierwiastkiem w organizmach żywych jest wodór, którego jądra — protony, odgrywają podstawową role w otrzymywaniu obrazów MR. W związku z tym omówienie pojęcia spinu ograniczymy do przypadku spinu równego [math]\frac{1}{2}[/math].
- Zjawisko takie jak: rozszczepienie w niejednorodnym polu magnetycznym wiązki atomowej na dwie składowe, zaobserwowane przez Sterna i Gerlacha w roku 1922, czy dubletowa struktura widm pierwiastków alkalicznych nie zostały wyjaśnione w ramach teorii budowy atomu zaproponowanej przez Bohra. Doświadczenie Sterna-Gerlacha, jak i badania spektroskopowe wskazywały na nieuwzględnienie w teorii Bohra pewnej wielkości fizycznej — nieznanego, dodatkowego stopnia swobody elektronu.
- W roku 1925 Uhlenbeck i Goudsmit wprowadzają pojecie spinu, jako wewnętrznego momentu pędu elektronu. Uhlenbeck i Goudsmit przyjęli, iż elektron wiruje[1] wokół własnej osi, co w naturalny sposób umożliwiło im wytłumaczenie istnienia dodatkowego stopnia swobody oraz wyjaśnienie dubletowej struktury widm pierwiastków alkalicznych. Obecnie wiadomo, iż obraz elektronu jako wirującej kulki zaproponowany przez Uhlenbecka i Goudsmita jest nieprawidłowy. W ramach Mechaniki Kwantowej, spin należy rozumieć jako wyraz istnienia stanów polaryzacyjnych funkcji falowej (w przypadku elektronu, protonu, neutronu i niektórych jąder będą to dwa stany polaryzacyjne). Spin jest własnością cząstek, taką samą jak np. masa lub ładunek, ale obserwowalną dopiero w eksperymentach ujawniających kwantową naturę materii (często można spotkać się ze stwierdzeniem, iż spin jest kwantową własnością cząstek). Spin jest także składową całkowitego momentu pędu, niezwiązana z ruchem, można go zatem również interpretować jako własny (wewnętrzny) moment pędu cząstki.
Spin i moment magnetyczny jądra atomowego
Jądra atomowe zawierające nieparzystą liczbę protonów lub neutronów mają niezerowy własny moment pędu [math]\vec{I}[/math] (spin) oraz związany z nim moment magnetyczny. Zgodnie z regułami opisu wielkości wektorowych w mechanice kwantowej, jednocześnie może być obserwowalna tylko długość wektora oraz wartość jednej z jego składowych (tzw. rzut tego wektora na wyróżnioną oś, nazywaną osią kwantowania). W przypadku wektora własnego momentu pędu jądra atomowego jego długość wynosi [2]:
gdzie:
[math]I[/math] oznacza liczbą kwantową o wartości całkowitej lub połówkowej.
Składowa [math]z[/math] momentu pędu wyraża się następującym wzorem [2]:
Możliwych jest zatem [math]2I+1[/math] orientacji spinu jądra względem wyróżnionego kierunku, odpowiadających możliwym wartościom jądrowej magnetycznej liczby kwantowej [math]m_{I}[/math]. W przypadku protonu (jądra atomu wodoru), mamy:
Moment magnetyczny związany jest ze spinem następującą zależnością:
Stała proporcjonalności [math]\gamma[/math] to tzw. jądrowy stosunek giromagnetyczny. Również i w przypadku jądrowego momentu magnetycznego można zmierzyć jednocześnie tyko jego długość i rzut na wyróżnioną oś [math]z[/math] wynoszący:
Na moment magnetyczny umieszczony w polu magnetycznym [math]\vec{B}[/math], działa pewien moment siły, starający się ustawić momentu magnetycznego zgodnie z kierunkiem pola [math]\vec{B}[/math]. Energia potencjalna tego oddziaływania wynosi:
Zgodnie z prawami termodynamiki układ fizyczny dąży do stanu, w którym jego energia wewnętrzna osiągnie wartość minimalną. Rozważmy pole [math]\vec{B}[/math], posiadające tylko składową wzdłuż osi [math]z[/math] układu odniesienia, czyli [math]\vec{B} = \left[ 0, 0, B_{z}\right] [/math]. W przypadku protonu, posiadającego ładunek dodatni, orientacji momentu pędu zgodnej z kierunkiem pola [math]\vec{B}[/math] będzie odpowiadać energia potencjalna:
natomiast orientacji antyrównoległej:
Ustawienie najkorzystniejsze energetycznie odpowiada więc sytuacji, kiedy składowa [math]z[/math] spinu ustawiona jest w równolegle do kierunku pola [math]\vec{B}[/math] (magnetyczna liczba kwantowa [math]m_{I}=\frac{1}{2}[/math]).
Moment magnetyczny w stałym zewnętrznym polu magnetycznym
Rozwiązanie równań Schrödingera dla przypadku statycznego pola magnetycznego nie jest skomplikowanym zadaniem. Niemniej interpretacja fizyczna otrzymanych wyników może sprawić pewne trudności. Ponadto w obrazowaniu MRI stosuje się nie tylko stałe pole magnetyczne lecz również odpowiednie serie impulsów pobudzających (tzw. impulsów pobudzających [math]\pi/2[/math] lub [math]\pi[/math]). Okazuje się, że w wielu przypadkach, zadowalający opis zjawiska rezonansu magnetycznego, uzyskuje się stosując tzw. model wektorowy, który jest podobny do modelu opisującego precesję symetrycznego bączka w polu grawitacyjnym.
Rozważmy moment magnetyczny znajdujący się w stałym polu magnetycznym o następującej indukcji:[math]\vec{B}_0 =\left[0, 0, B_{0}\right][/math].
Szybkość zmian momentu pędu ciała ([math]\vec{I}[/math]) jest równa momentowi siły ([math]\vec{N}[/math]) działającemu na to ciało:
Moment magnetyczny, związany z wewnętrznym momentem pędu jądra, wynosi:
Po przekształceniu powyższego równania dostajemy:
W polu magnetycznym [math]\vec{B}_0[/math] na moment magnetyczny będzie działa moment siły:
Podstawiając równanie na moment pędu do równania na moment siły otrzymujemy zależność opisującą ruch momentu magnetycznego:
ponieważ:
ostatecznie równanie (Equation 13) możemy zapisać jako układ trzech równań:
gdzie: [math]\omega_{0}=\gamma B_{0}[/math]
Rozwiązanie równania na wielkość składowej z wektora momentu magnetycznego jest proste i wynosi:
W celu uzyskania równań na dwie pozostałe składowe wyznaczmy druga pochodną pierwszego równania w układzie (Equation 15) i podstawmy ją do równania drugiego we wspomnianym układzie:
Podstawiając teraz drugie równanie z układu (Equation 17) do równania pierwszego układu (Equation 17) dostajemy:
Jest to równanie oscylatora harmonicznego o następującym rozwiązaniu:
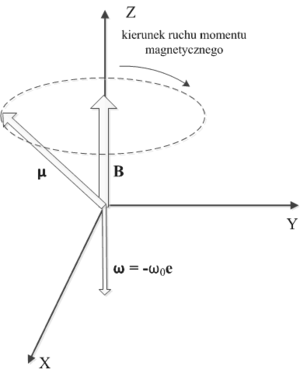
gdzie stałe A oraz [math]\phi_0[/math] wynikają z warunków początkowych. Widzimy, że składowa x momentu magnetycznego drga z częstością [math]-\omega_0[/math]. Przyczyna pojawienia się znaku "-" w rozwiązaniu została wyjaśniona na rys. 1. Podstawiając równanie (Equation 19) do drugiego równania w układzie (Equation 15) dostajemy rozwiązanie na wielkość składowej y momentu magnetycznego:
Ostatecznie otrzymaliśmy następujące rozwiązanie ruchu wektora momentu magnetycznego w stałym polu magnetycznym:
gdzie:
[math]A, \phi_0, \mu^{0}_{z} [/math] wynikają z warunków początkowych.
Na podstawie równania (Equation 21) możemy wyciągnąć następujące wnioski:
- składowa z momentu magnetycznego (równoległa do osi z i pola magnetycznego) zachowuje stały kierunek w przestrzeni,
- składowa x oraz y momentu magnetycznego zakreśla w płaszczyźnie X-Y okrąg.
Złożenie ruchu momentu magnetyczne w płaszczyźnie X-Y ze stałym kierunkiem składowej z daje wypadkowy ruch nazywany precesją (w tym przypadku jest to precesja momentu magnetycznego wokół kierunku stałego pola magnetycznego). Wektor momentu magnetycznego wykonuje ruch precesyjny z prędkością kątową (odpowiadającej częstości kołowej):
nazywaną częstością Larmour'a. Składowe x oraz y momentu magnetycznego można zapisać w wygodniejszy sposób stosują formalizm liczb zespolonych. Pomnóżmy trzecie równanie w układzie (Equation 21) przez liczbę [math]i=\sqrt{-1}[/math] i dodajmy do drugiego równania w układzie (Equation 21):
Wprowadźmy wielkość:
Wektor [math]\vec{\mu}_T[/math] będziemy od tej chwili nazywali składową poprzeczną (ang. transversal) momentu magnetycznego. Z kolei wektor [math]\vec{\mu}_z[/math] będziemy dalej oznaczali symbolem [math]\vec{\mu}_L[/math] i nazywali składową podłużną momentu magnetycznego (ang. longnitudal). Innym dogodny sposób matematycznego opisu zjawiska precesji momentu magnetycznego, który będziemy stosowali, wykorzystuje macierz obrotu:
gdzie:
[math]\mu_L^0[/math] — rzut momentu magnetycznego na os Z w chwili początkowej,
[math]\mu_T^0[/math] — rzut momentu magnetycznego na płaszczyznę X-Y w chwili początkowej,
[math]\phi_0[/math] — kąt jaki tworzy rzut momentu magnetycznego na płaszczyznę X-Y z osią X w chwili początkowej,
[math]P = \left[
\begin{array}{ccc}
\cos(\omega_0 t) & \sin(\omega_0 t) & 0 \\
\\
-\sin(\omega_0 t) & \cos(\omega_0 t) & 0 \\
\\
0 & 0 & 1
\end{array}
\right] [/math] — macierz obrotu.
We wzorze (Equation 41) skorzystano z własności trygonometrycznych sinusa i cosinusa:
Namagnesowanie próbki
Namagnesowanie, to całkowity moment magnetyczny, przypadający na jednostkę objętości [math]\Delta V[/math]:
Rozłóżmy wektor namagnesowania na dwie składowe: tzw. podłużną ([math]\vec{M}_L[/math]),to jest równoległą do kierunku pola magnetycznego oraz składową poprzeczną ([math]\vec{M}_T[/math]), leżącą w płaszczyźnie prostopadłej do kierunku pola magnetycznego:
Ile wynosi namagnesowanie poprzeczne próbki?
Składową poprzeczną namagnesowania będziemy oznaczali wektorem [math]\vec{M}_T[/math]. Załóżmy, że w próbce znajduje się N takich samych jąder posiadających moment magnetyczny. Momenty te mają losową orientację przestrzeni. W pewnej chwili, zostaje włączone stałe pole magnetyczne. Stałe A oraz [math]\phi_0[/math] dla każdego momentu magnetycznego wyznaczamy na podstawie orientacji momentu magnetycznego w chwili łączenia pola. Dla każdego jądra magnetycznego stała A wynikająca z warunków początkowych jak to faza początkowa [math]\phi_0[/math] jest dowolna. W związku z czym:
gdzie [math]\vec{\mu}_T[/math] to składowa poprzeczna wektoru momentu magnetycznego, zgodnie ze wzorem (Equation 24).
Ile wynosi namagnesowanie próbki, czyli namagnesowanie podłużne?
Przypominamy, że rozważamy cząstkę lub jądro atomowe, znajdujące się w zewnętrznym polu magnetycznym [math]\vec{B}_{0}[/math], skierowanym równolegle do osi [math]z[/math]. Składowa [math]z[/math] tego pola wynosi [math]B_{0}[/math]. W celu uproszczenia problemu przyjmujemy, że cząstka lub jądro atomowe posiada spin równy [math]\frac{1}{2}[/math] (np. proton). Moment magnetyczny cząstki lub jądra atomowego może ustawić się zgodnie lub przeciwnie do kierunku zewnętrznego pola magnetycznego. W szczególności składowa [math]z[/math] momentu magnetycznego, przyjmie kierunek równoległy bądź antyrównoległy do pola [math]B_{0}[/math], skierowanego wzdłuż osi [math]z[/math]. Jak wiemy, układy fizyczne dążą do osiągnięcia stanu, w którym uzyskają minimum energii. Energia potencjalna momentu magnetycznego w zewnętrznym polem magnetycznym wynosi:
Rozwijając powyższy wzór dla rozważanego przez nas przypadku, otrzymujemy:
gdzie:
[math]m_{I}=\pm\frac{1}{2}[/math]
Rzutowi momentu magnetycznego równoległemu do osi [math]z[/math], czyli dla [math]m_{I}=\frac{1}{2}[/math], odpowiada energia potencjalna:
natomiast rzutowi antyrównoległemu:
Jak widać ustawienie równoległe spinu i momentu magnetycznego protonu względem pola [math]B_{0}[/math] jest korzystniejsze energetycznie niż ustawienie antyrównoległe. Należy się zatem spodziewać, iż w zewnętrznym polu magnetycznym częściej będzie występować sytuacja, kiedy moment magnetyczny ustawi się w kierunku tego pola. Namagnesowanie podłużne powstaje zatem w wyniku nierównomiernego obsadzenia przez cząstkę lub jądro stanów o spinie skierowanym zgodnie lub przeciwnie do kierunku oddziałującego pola magnetycznego. W celu obliczenia, jaka będzie różnica w ilości obsadzeń poszczególnych stanów energetycznych, skorzystamy z rozkładu Boltzmana. Stosunek liczby cząstek obsadzających dwa stany energetyczne jest równa:
gdzie:
[math]T[/math] — temperatura,
[math]k_{b}[/math] — stała Boltzmana,
[math]N_{\pm}[/math] — liczba cząstek o spinie skierowanym odpowiednio równolegle i antyrównolegle do pola [math]B_{0}[/math].
Podstawiając do wzoru (Equation 34) wyznaczone wcześniej energie potencjalne, odpowiadające dwóm różnym orientacjom spinu w polu [math]B_{0}[/math] dostajemy:
W temperaturze pokojowej, różnice obsadzeń poszczególnych poziomów energetycznych są nieznaczne, dlatego skorzystamy z przybliżenia:
Różnica w ilości obsadzeń poszczególnych poziomów energetycznych jest zatem równa:
gdzie:
[math]N_{t}[/math] to liczba wszystkie jąder atomu wodoru w badanej próbce.
Czynnik [math]\frac{\gamma\hbar B_{0}}{k_{b}T}[/math] w temperaturze ciała ludzkiego [math]T=310K[/math] i polu magnetycznym [math]B_{0}=1T[/math] jest równy:
Wynik ten oznacza, że na każdy milion protonów o spinie skierowanym przeciwnie do pola magnetycznego, przypada milion plus siedem protonów o spinie skierowanym równolegle do pola i ta niewielka nadwyżka protonów w stanie o korzystniejszej energii jest odpowiedzialna za namagnesowanie próbki. Wartość nadwyżki wydaje się być niezwykle mała. Należy jednak pamiętać, że ilość protonów jaka występuje w organizmie ludzkim jest niezmiernie duża, co umożliwia rejestrację wytworzonego namagnesowania. Jeden gram wody zawiera [math]\frac{1}{8}[/math] mola atomów wodoru. W jednym molu materii występuje [math]6.023\cdot10^{32}[/math] cząsteczek, a zatem gram wody zawiera [math]N_{t} = 6.68\cdot10^{22}[/math] atomów wodoru. Nadwyżka [math]\Delta N[/math] wynosi zatem [math]\Delta N\approx 2.2\cdot10^{17}[/math] protonów. Całkowity podłużny moment magnetyczny wytworzony przez 1 gram wody wynosi:
Z kolei namagnesowanie to całkowity moment magnetyczny na jednostkę objętości. Jeden gram wody zajmuje objętość [math]10^{-6}\mathrm m^{-3}[/math] a zatem namagnesowanie wytworzone 2 jednym gramie wody w polu magnetycznym o wartości indukcji [math]B_{0}=1[/math]T w temperaturze [math]T=310[/math]K wyniesie:
Zmiana orientacji wektora namagnesowania. Magnetyczny Rezonans Jądrowy
W poprzednim rozdziale dowiedzieliśmy się, że efektem wprowadzenia jąder w stałe pole magnetyczne jest wykonywanie przez momenty magnetyczne ruchu precesyjnego wokół kierunku wektora pola magnetycznego, skutkiem czego pojawia się namagnesowanie próbki. Niestety, pomiar wielkości uzyskanego w ten sposób namagnesowania jest niemożliwy do przeprowadzenia. Namagnesowanie ma ten sam kierunek co wywołujące je pole magnetyczne. W celu pomiaru wielkości namagnesowania próbki niezbędne jest zmiana orientacji wektora [math]\vec{M}[/math]. Dokonuje się to poprzez wprowadzenie próbki w dodatkowe, zmienne pole magnetyczne. Proces ten opiszemy w niniejszym rozdziale.
Ewolucję wektora namagnesowania można opisać równaniem podobnym do równania (Equation 13):
Rozważmy teraz konfigurację dwóch pól magnetycznych — pola statycznego i pola zmiennego w czasie, mającego niezerowe składowe tylko w płaszczyźnie prostopadłej do kierunku pola stałego. Niech zmienne pole magnetyczne ma postać:
Indukcja zmiennego pola magnetycznego [math]\vec{B}_1[/math] jest rzędu [math]10^{-5}[/math] T, a zatem jest znacznie mniejsza od indukcji statycznego pola magnetycznego [math]\vec{B}[/math]. Pole [math]\vec{B}_1[/math] nazywane jest impulsem pobudzającym (ang. Radio Frequency, RF), włączane jest bowiem na krótki okres czasu (co wyjaśnimy dalej). Impuls RF wytwarza się za pomocą cewek w postaci fali elektromagnetycznej. Okazuje się, że pole opisane wzorem (Equation 41) możemy rozłożyć na dwa pola, rotujące w płaszczyźnie x-y w przeciwne strony:
Pierwsza składowa pola [math]\vec{B}_{1_R}[/math] rotuje przeciwnie do wskazówek zegara, zaś druga składowa [math]\vec{B}_{1_l}[/math] w kierunku przeciwnym. W zależności od tego, jaką orientację posiadał jądrowy moment magnetyczny (równoległą lub antyrównoległą do osi [math]z[/math]), jedna z tych składowych będzie drgała w kierunku ruchu precesyjnego spinu, druga zaś w kierunku przeciwnym. Składowa drgająca w kierunku przeciwnym będzie "niewidoczna dla momentu magnetycznego" i nie wpłynie na jego orientację. Pole drgające w kierunku przeciwnym do ruchu precesyjnego momentu magnetycznego wywoła pewne drugorzędowe efekty, które nie będą omawiane w niniejszej pracy. Ruch momentu magnetycznego, w przypadku superpozycji dwóch pól — statycznego [math]B_{0}[/math] oraz zmiennego [math]B_{1}\left(t\right)[/math] opisuje zatem następujące równanie:
gdzie: [math]\vec{B}_{0} = \left[0, 0, B_{0}\right][/math], [math]B_{1}\left(t\right) = B_{1}\left[\cos\left(\omega_1 t\right),-sin\left(\omega_1 t\right),0\right])[/math].
Wprowadźmy dwa układy współrzędnych: Układ Laboratoryjny U oraz układ U' obracający się z częstością zmiennego pola magnetycznego ([math]\omega_1[/math]). Osie z oraz z' odpowiednio układu U oraz U' są do siebie równoległe. Stałe pole magnetyczne jest skierowane wzdłuż tych osi. Zapiszmy równanie (Equation 44) w układzie U ' .
Zgodnie z zasadami transformacji wektorów pomiędzy różnymi układami współrzędnych, równanie (Equation 44) w układzie U' będzie miało postać:
które można również zapisać w formie:
gdzie: [math]\vec{B}_{eff} = \left[\left(B_{0} - \frac{\omega_1}{\gamma}\right)\vec{e}_z + B_{1}\vec{e}_x\right][/math].
Zjawisko Magnetycznego Rezonansu Jądrowego w ujęciu klasycznym
Przeanalizujmy równanie (Equation 46). W obracającym się układzie odniesienia jądrowy moment magnetyczny zachowuje stałe położenie. Wzdłuż osi z' układu U' obserwujemy składową statycznego pola magnetycznego [math]B_0\vec{e}_z[/math] oraz pole [math]\frac{\omega_1}{\gamma}\vec{e}_z[/math], które powstaje w wyniku przejścia z układu laboratoryjnego U do układu U' . Dodatkowo w płaszczyźnie X'-Y' obserwujemy statyczne pole magnetyczne [math]\vec{B}_1\vec{e}_x[/math]. W wyniku złożenia tych trzech pół, powstaje wypadkowe pole [math]\vec{B}_{eff}[/math], wokół którego moment magnetyczny zaczyna dokonywać precesji.
Rozpatrzmy następujące przypadki:
1. Częstość [math]\omega_1[/math] wirującego pola [math]\vec{B}_1[/math] jest bardzo niewielka ([math]\omega_1\approx0[/math]).
- Przypominamy, że [math]B_0\gt \gt B_1[/math], wtedy:
- [math]\vec{B}_{eff} = B_{0}\vec{e}_z[/math],
- innymi słowy, dodatkowe, rotujące pole magnetyczne nie wpływa na orientację momentów magnetycznych oraz namagnesowania.
2. Częstość [math]\omega_1[/math] wirującego pola [math]\vec{B}_1[/math] spełniona warunek [math]\frac{\omega_1}{\gamma}\gt \gt B_0)[/math], wtedy:
- Przypominamy, że [math]B_0\gt \gt B_1[/math]
i wtedy: - [math]\vec{B}_{eff} = -\frac{\omega_1}{\gamma}\vec{e}_z[/math]
- czyli zjawisko precesji momentów magnetycznych nadal odbywa się wokół osi z' , z tą różnicą, iż ulega zmianie kierunek precesji, zaś dodatkowe, rotujące pole magnetyczne nie wpływa na orientację momentów magnetycznych oraz namagnesowania [math]\vec{M}[/math].
3. Częstość rotującego pola magnetycznego [math]\vec{B}_1[/math] spełnia warunek [math]\omega_1 = \gamma B_{0}[/math], wtedy:
- [math]\vec{B}_{eff} = B_1\vec{e}_x[/math],
- co oznacza, że wektor namagnesowania zaczyna wykonywać ruch precesyjny wokół pola magnetycznego [math]B_1\vec{e}_x[/math]. Ponownie : przypominamy, że [math]B_1\lt \lt B_0[/math]. Jak widać, przy pomocy pola magnetycznego o niewielkiej indukcji, lecz odpowiednio dobranej częstości, możliwa jest zmiana orientacji wektora namagnesowania. Jest to zjawisko Magnetycznego Rezonansu Jądrowego. Występowanie w nazwie zjawiska termin rezonans (kojarzony najczęściej z obwodami elektrycznymi), jest jak najbardziej uzasadnione, ponieważ za pomocą niewielkiego zaburzenia o periodycznym charakterze (ale odpowiednio dobranej częstości), doprowadziliśmy do znaczących zmian w układzie. Częstość ruchu precesyjnego wektora namagnesowania wokół pola [math]\vec{B}_1[/math] wynosi:
- Częstość [math]\Omega[/math] jest nazywana częstością Rabbiego. W trakcie czasu [math]\tau\gt [/math] namagnesowanie zakreśli kąt [math]\Theta[/math] równy:
Podsumowując, po wprowadzeniu próbki w stałe pole magnetyczne o wartości indukcji B_0, momenty magnetyczne poszczególnych jąder zaczynają : wykonywać ruch precesyjny z częstością Larmour'a [math]\omega_0=\gamma\ B_0[/math]. Pojawia się wypadkowe namagnesowanie próbki w kierunku : : stałego pola magnetycznego. Wprowadzając dodatkowe pole magnetyczne o wartości indukcji [math]B_1[/math], wirujące w płaszczyźnie prostopadłej do pola [math]B_0[/math], możliwa jest zmiana orientacji wektora namagnesowania, o ile częstość wirowania pola [math]\vec{B}_1[/math] jest równa częstości [math]\omega_0[/math] precesji Larmour'a.
Podsumowując:
- Pod wpływem zewnętrznego, statycznego pola magnetycznego, skierowane wzdłuż osi [math]z[/math] spiny wykonują precesję. Składowa [math]z[/math] wartości oczekiwanej spinu jest stałą w czasie, składowe poprzeczne wykonują ruch wirowy w płaszczyźnie [math]x-y[/math].
- Różnym ułożeniom spinu względem pola magnetycznego odpowiadają różne energie potencjalne. W przypadku spinu równego [math]\frac{1}{2}[/math]
istnieją dwa poziomy energetyczne, które będą obsadzane przez jądra zgodnie z rozkładem Bolzmana. Poziom związany z równoległym do zewnętrznego pola magnetycznego rzutem spinu jest korzystniejszy energetycznie, dlatego będzie obsadzany częściej. - Desynchronizacja ruchu wirowego wartości oczekiwanej spinów w płaszczyźnie [math]x-y[/math] uniemożliwi powstanie namagnesowania poprzecznego. Obserwujemy tylko namagnesowanie podłużne.
- Pod wpływem odpowiednio dobranego pola magnetycznego, można doprowadzić do przejść rezonansowych. Jądro mające spin w korzystniejszym stanie energetycznym, przejdzie do stanu, o wyższej energii związanej z oddziaływaniem spinu z polem magnetycznym. Zanika równowaga termodynamiczna w obsadzeniu stanów, a wraz z nią składowa [math]z[/math] wartości oczekiwanej spinu i związane nią namagnesowanie podłużne.
- Jednocześnie, w wyniku synchronizacji w płaszczyźnie [math]x-y[/math] wartości oczekiwanej spinów tych jąder atomowych, które uległy przejściu rezonansowemu, zaczyna powstawać namagnesowanie poprzeczne.
- Obserwowane namagnesowanie podłużne zanika, podczas gdy narasta namagnesowanie podłużne. Obserwujemy zatem efekt, odchylania się namagnesowania od osi [math]z[/math] w kierunku płaszczyzny [math]x-y[/math].
- Po pewnym czasie namagnesowanie podłużne zanika, a namagnesowanie poprzeczne osią maksymalną wartość.
- Zmianom kierunku i wielkości namagnesowania towarzyszy zmiana indukcji pola elektrycznego, która może być rejestrowana przez cewki.
Typowe wartości częstości Larmour'a oraz częstości Rabbiego
Opisując zmiany wielkości fizycznych w czasie niejednokrotnie posługujemy się częstością wyrażaną w Hz. W takim przypadku wzór: (Equation 22) przyjmie nastepującą postać:
Z tego względu, częstą praktyką podawanie jest w tablicach fizycznych stałej [math]\frac{\gamma}{2\pi}[/math] zamiast samej wartości współczynnika giromagnetycznego γ.
| Jądro | Spin | [math]\frac{\gamma}{2\pi}[/math] [math]\left[\frac{\textrm{MHz}}{\textrm{T}}\right][/math]. |
|---|---|---|
| [math]^1H[/math] | [math]\frac{1}{2}[/math] | 42,58 |
| [math]^{13}C[/math] | [math]\frac{1}{2}[/math] | 10,71 |
| [math]^{14}N[/math] | [math]1[/math] | 3,08 |
| [math]^{17}O[/math] | [math]\frac{1}{2}[/math] | 42,58 |
| [math]^{23}Na[/math] | [math]\frac{3}{2}[/math] | 11,27 |
| [math]^{39}K[/math] | [math]\frac{3}{2}[/math] | 1,99 |
| [math]^{43}Ca[/math] | [math]\frac{7}{2}[/math] | 2,86 |
Jak można zauważyć, największą wartością momentu magnetycznego charakteryzują się jądra atomu wodoru, czyli protony. Częstość precesji Larmour'a dla protonów umieszczonych w polu magnetycznym o indukcji [math]B_0=1[/math] T osiągnie wielkość:
Dodatkowe, zmienne pola magnetyczne [math]\vec{B}_1[/math], stosowane do zmiany orientacji wektora namagnesowania, mają niewielkie wartości, rzędu [math]10^{-5}[/math]T. Po wprowadzeniu próbki zawierającej jądra atomu wodoru w dodatkowe pole magnetyczne [math]\vec{B}_1[/math], wirujące w płaszczyźnie prostopadłej do kierunku pola statycznego, namagnesowanie zaczyna wykonywać obrót w płaszczyźnie równoległej do kierunku pola statycznego z częstością Rabbiego równą:
Impulsy [math]\pi[/math] oraz [math]\frac{\pi}{2}[/math]
Jak dowiedzieliśmy się w poprzednich rozdziałach, przy pomocy rotującego pola magnetycznego o odpowiednio dobranej częstości, możemy zmienić orientacje wektora namagnesowania. Jest to o tyle ważne, iż wektor ten wywołuje pole magnetyczne dużo mniejsze z w porównaniu do wartości pola statycznego [math]\vec{B}_0[/math], do którego jest równoległy. Uniemożliwia to pomiar wartości magnetyzacji próbki. Zmianę orientacji wektora namagnesowania określa się za pomocą kąta, o jaki odchyla się on od kierunku statycznego pola magnetycznego [math]\vec{B}_0[/math], które leży wzdłuż osi Z przyjętego przez nas układu współrzędnych. Kąt ten można wyliczyć za pomocą wzoru na częstość Rabbiego. Jeśli wektor namagnesowania w trakcie rezonansu wykonuje precesję wokół pola [math]B_1[/math] z częstością:
to w czasie τ zakreśli on kąt:
Szczególną rolę w diagnostyce MRI odgrywają obroty wektora namagnesowania o kąt [math]\Theta = \frac{\pi}{2}[/math] oraz [math]\Theta = \pi[/math]. Pole magnetyczne, wywołujące takie zmiany nazywamy odpowiednio impulsami [math]\frac{\pi}{2}[/math] oraz [math]\pi[/math]. Czas trwania tych impulsów możemy łatwo oszacować. Przyjmując wielkość indukcji pola [math]B_1[/math] na [math]10^{-5}[/math] T oraz współczynnik giromagnetyczny dla protonów, dostajemy:
- dla impulsu [math]\frac{\pi}{2}[/math], [math]\tau = \frac{\Theta}{\gamma B_1} = \frac{\frac{\pi}{2}}{2\pi\cdot 42,577 \left[\frac{\textrm{MHz}}{\textrm{T}}\right]\cdot 10^{-5}\textrm{T}}\approx 580\mu s[/math]
- dla impulsu [math]\pi[/math], [math]\tau = \frac{\Theta}{\gamma B_1} = \frac{\pi}{2\pi\cdot 42,577 \left[\frac{\textrm{MHz}}{\textrm{T}}\right]\cdot 10^{-5}\textrm{T}}\approx 1060\mu s[/math]
Procesy Relaksacji
Procesy relaksacji podpis pod rysunkiem:
Składowa poprzeczna wektora, oznaczona kolorem czerwonym, jest sumą trzech wektorów o jednostkowej długości, rotujących w płaszczyźnie X-Y i oznaczonych kolorem niebieskim. W chwili [math]t=0[/math] (punkt A.), wektory składowe rotują w płaszczyźnie X-Y w tej samej fazie, dając wektor wypadkowy o długości trzech jednostek. Po pewnym czasie [math]\Delta t[/math] (punkt B.) jeden z wektorów składowych zmienia orientację o kąt [math]\frac{\pi}{2}[/math], w efekcie czego długość składowej poprzecznej wektora wypadkowego maleje do dwóch jednostek, pojawia się natomiast składowa podłużna wektora wypadkowego (oznaczona kolorem zielonym) o długości jednej jednostki. Po kolejnym czasie Po pewnym czasie [math]\Delta t[/math] (punkt C.), ruch pozostałych w płaszczyźnie X-Y rotujących wektorów ulega rozfazowaniu, co powoduje dalszy zanik składowej poprzecznej wektora wypadkowego, ale nie zwiększa długości jego składowej podłużnej. Po upływie kolejnej jednostki czasu [math]\Delta t[/math] (punkt D.), jeden z wektorów składowych, rotujący w płaszczyźnie X-Y zmienia orientację o kąt [math]\frac{\pi}{2}[/math]. Składowa poprzeczna wektora wypadkowego ulega skróceniu do jednej jednostki, zaś składowa podłużna osiąga długość dwóch jednostek. Po zmianie orientacji ostatniego wektora składowego (punkt E.), składowa poprzeczna wektora wypadkowego zanika, zaś składowa podłużna osiąga maksymalną długość trzech jednostek.
W rozdziałach [[1]], [[2]] oraz [[3]] omówiliśmy dwa następujące podstawowe elementy zjawiska rezonansu magnetycznego:
- Wprowadzenie próbki składającej się z atomów wodoru w statyczne pole magnetyczne, skutkiem czego pojawiło się namagnesowanie próbki w kierunku tego pola.
- Pobudzenie próbki rotującym w płaszczyźnie prostopadłej do pola statycznego, polem magnetycznym o małej indukcji lecz odpowiednio dobranej częstości, co doprowadziło do zmiany orientacji wektora namagnesowania.
Poruszyliśmy również kwestie doboru czasu impulsu rotującego pola magnetycznego, tak aby zmienić orientację wektora namagnesowania o kąt [math]\pi[/math] lub [math]\frac{\pi}{2}[/math]. Po obróceniu magnetyzacji o wymagany kąt, impulsowe pole magnetyczne jest wyłączane i dokonywany jest pomiar namagnesowania próbki. Co dalej dzieje się z wektorem magnetyzacji ? Obrót wektora namagnesowania jest niczym innym jak wytrąceniem układu z położenia równowagi termodynamicznej. Jak pamiętamy z pierwszych rozdziałów dotyczących MRI, momenty magnetyczne jąder atomowych starają ustawić się w kierunku pola magnetycznego. Układ będzie zatem dążył do powrotu do stanu równowagi. Przypominamy, iż wyróżniliśmy dwie składowe namagnesowania: namagnesowanie podłużne ([math]\vec{M}_L[/math] oraz namagnesowanie poprzeczne [math]\vec{M}_T[/math]. Przyjmijmy, że umieszczenie próbki w polu magnetycznym wywołuje namagnesowanie o wartości [math]M_0[/math] i rozważmy składowe namagnesowania w układzie rotującym U' w następujących przypadkach:
1.Włączone pole statyczne, wtedy:
2. Zadziałanie na próbkę impulsem [math]\frac{\pi}{2}[/math], po którym magnetyzacja wynosi:
.
Interesuje nas teraz przejście układu ze stanu (2) do stanu (1). Proces powrotu układu do stanu równowagi nazywamy relaksacją.
Okazuje się, że proces odbudowywania się namagnesowania podłużnego trwa dłużej, niż zanik namagnesowania poprzecznego. W związku z tym, będziemy wyróżniali relaksację podłużną, to jest odbudowywanie się składowej podłużnej namagnesowania oraz relaksację poprzeczną, czyli zanik składowej poprzecznej magnetyzacji. Przyczynę różnego czasu procesów relaksacji podłużnej i poprzecznej są następujące.
Relaksacja podłużna
Podstawową przyczyną przechodzenia jąder atomowych ze stanu wzbudzonego do podstawowego po wyłączeniu impulsu pobudzającego są oddziaływania spinów poszczególnych jąder z siecią krystaliczną (tzw. oddziaływania spin-sieć). W wyniki tych przejść zanika oczywiście również składowa poprzeczna namagnesowania. Inne procesy, które mają wpływ na powrót jąder do stanu równowagi i odbudowę składowej podłużnej magnetyzacji to:
- Fluktuacje pola magnetycznego wytworzone przez otoczenie danego jadra atomowego, np. przez cząsteczkę wody która posiada własny moment magnetyczny. Chaotyczne ruchy cząsteczki wody, mogą wytworzyć zmienne w czasie pole magnetyczne wywołujące przejścia momentów magnetycznych ze stanu wzbudzonego do podstawowego.
- Oddawanie energii do otoczenia poprzez oddziaływania elektryczne.
- Oddziaływania paramagnetyczne.
Warto jednak zwrócić uwagę, że fluktuacje pola magnetycznego będą prowadziły do przejść jąder atomowych ze stanu wzbudzonego do stanu podstawowego pod warunkiem, że częstość wywołanego przez nie lokalnego pola magnetycznego będzie zbliżona do częstości precesji Larmour. Czas relaksacji podłużnej, który oznaczany jest jako tzw. czas [math]T_1[/math] wynosi zwykle od kilkuset ms do nawet 2 sekund.
Relaksacja poprzeczna
Oddziaływania wymienione w punktach 1-3 poprzedniego rozdziały, które powodują przejścia jąder atomowych ze stanu wzbudzonego do stanu podstawowego, powodują jednocześnie zanik składowej poprzecznej namagnesowania. Składowa ta jednak zanika także z innych powodów. Impuls pobudzające, nie tylko zmienia orientację momentów magnetycznych, lecz również synchronizuje ich ruchy precesyjne. Fluktuacje pola magnetycznego mogą łatwo tę synchronizacje zaburzyć, ponieważ w tym przypadku dowolna fluktuacja lokalnego pola magnetycznego w kierunku pola statycznego [math]\vec{B}_0[/math] zmieni częstość rotacji momentów magnetycznych w płaszczyźnie X-Y. Również oddziaływania spinów sąsiednich jąder atomowych przyczyniają się do zakłócenia synchronizacji (oddziaływania te nazywamy oddziaływaniami spin-spin). Kolejną przyczyną szybszego zaniku składowej poprzecznej namagnesowania są niejednorodności statycznego pola magnetycznego spowodowane ograniczeniami w dokładności wykonania urządzenia MRI oraz zaburzenia powstałe w otoczeniu skanera. Czas relaksacji poprzecznej, który oznaczany jest jako tzw. czas [math]T_2[/math] jest o rząd wielkość mniejszy od czasu [math]T_1[/math] i wynosi zwykle od kilkudziesięciu di kilkuset ms. Ideę różnego czasu relaksacji rotujących składowych pewnego wektora zaprezentowano symbolicznie na rys. 3. Należy pamiętać, iż w rzeczywistości procesy relaksacji są znacznie bardziej skomplikowane, zaś ilustracja rys. 3 ma charakter jedynie poglądowy.
W klasycznej teorii rezonansu jądrowego zjawiska relaksacji opisuje w układzie rotującym (U' ) przy pomocy następujących fenomenologicznych równań:
W półklasycznego równaniu (Equation 46) opisującym zachowanie się namagnesowania w polu magnetycznym musimy uwzględnić procesy związane z relaksacją spinów.
Bloch wprowadził fenomenologiczne poprawki do tego równania opierając się na rozumowaniu, które można wyrazić następującymi równaniami:
gdzie: [math]M_x, M_y, M_z[/math] to odpowiednio długości poszczególnych składowych wektora namagnesowania.
Równanie Blocha
Podpis pod rysunkiem Ewolucja wektora magnetyzacji w układzie rotującym z prędkością kątową [math]\omega_0 = \gamma B_0[/math], związanym z momentem magnetycznym i w układzie laboratoryjnym.:
A — próbkę wprowadzono w stałe pole magnetyczne o indukcji [math]\vec{B}_0=B_0\vec{e}_z[/math]. Pole to wywołuje namagnesowanie próbki [math]\vec{M}_0[/math], które w układzie rotującym jak i laboratoryjnym ma tę sen sam kierunek [math]\vec{M}_0 = M_0\vec{e}_z[/math]. B — próbka zostaje pobudzona dodatkowym polem magnetycznym [math]\vec{B}_1[/math]. W układzie laboratoryjnym jest to pole rotujące, z częstością kątową [math]\omega_0[/math], podczas gdy w układzie rotującym ma ono ustalony kierunek. W celu uproszczenia rachunków pole [math]\vec{B}_1[/math] dobrano tak, aby w układzie rotującym miało kierunek równoległy do osi X. Wskutek oddziaływania momentów magnetycznych z polem [math]\vec{B}_1[/math], wektor namagnesowania zmienia orientację w następujący sposób. W układzie rotującym rozpoczyna ruch precesyjny wokół pola [math]\vec{B}_1[/math] (osi X' ), z częstością [math]\omega_1 = \gamma B_1[/math]. W układzie laboratoryjnym ruch namagnesowania jest złożeniem ruchu precesyjnego wokół pola [math]\vec{B}_1[/math] oraz ruchu precesyjnego wokół pola [math]\vec{B}_0[/math], w związku z czym w układzie laboratoryjnym wektor magnetyzacji zakreśla helisę o zwiększającej się średnicy. C — jeśli impulsem pobudzającym był impuls [math]\frac{\pi}{2}[/math], to zostanie on wyłączony po zmianie orientacji wektora namagnesowania o kąt [math]\frac{\pi}{2}[/math]. W chwili wyłączenia w układzie rotującym wektor magnetyzacji jest równoległy do pola [math]\vec{B}_1[/math], natomiast w układzie laboratoryjnym wektor magnetyzacji rotuje w płaszczyźnie X-Y. W tym momencie można rozpocząć pomiar namagnesowania za pomocą cewek. Rotujący wektor magnetyzacji wytwarza zmienne pole magnetyczne, które w cewkach, zgodnie z prawem Faraday'a indukuje siłę elektromotoryczną. D — po wyłączeniu pola pobudzającego [math]\vec{B}_1[/math], na skutek procesów relaksacji, momenty magnetyczne jąder przechodzą ze stanu wzbudzonego do stanu podstawowego. Efektem przejść jest powrót wektora magnetyzacji w kierunku pola magnetycznego [math]\vec{B}_0[/math].
Proste równanie opisujące zachowanie się momentów magnetycznych oraz magnetyzacji, które wyprowadziliśmy analogicznie jak się to czyni w przypadku ruchu bąka symetrycznego w polu grawitacyjnym nie jest pełne i powinno być rozszerzone o procesy relaksacji. Fenomenologiczne, klasyczne równanie opisującym zachowanie się namagnesowania w polu magnetycznym z uwzględnieniem procesów relaksacji nazywamy równaniem Blocha:
gdzie:
[math]\vec{B}_{eff} = \left[\left(B_{0} - \frac{\omega}{\gamma}\right)\vec{e}_z + B_{1}\vec{e}_x\right][/math]
Przykłady rozwiązania równań Blocha
W poniższym rozdziale podane zostały przykładowe rozwiązania równań Blocha dla wybranych konfiguracji pól magnetycznych.
Umieszczenie próbki w polu statycznym [math]\vec{B}_0 = B_0\vec{e}_z[/math]
Równanie Blocha jest równaniem opisującym ewolucję w czasie wektora magnetyzacji w układzie rotującym z częstością równa częstości precesji Larmour'a: [math]\omega = \gamma B_0[/math]. Konfiguracja pół magnetycznych w tym układzie, po wprowadzeniu próbki w statyczne pole magnetyczne wynosi:
- [math]B_1 = 0[/math],
- [math]\left[B_0 -\frac{\omega}{\gamma}\right]\vec{e}_z = 0[/math],
co prowadzi do następującego układu równań:
Zgodnie z obliczeniami przeprowadzonymi w rozdziale [4]. wiemy, że po umieszczeniu próbki w stałym polu magnetycznym, namagnesowanie może występować tylko w kierunku tego pola. Oznaczmy wartość tego namagnesowanie symbolem [math]M_0[/math]. Przy podanych warunkach początkowych dostajemy poniższe rozwiązanie układu równań (Equation 58):
Rozwiązanie w układzie laboratoryjnym uzyskamy, po przemnożeniu równania (Equation 59) przez macierz obrotu [math]P[/math]:
gdzie:
[math]P = \left[
\begin{array}{ccc}
\cos(\omega_0 t) & \sin(\omega_0 t) & 0 \\
\\
-\sin(\omega_0 t) & \cos(\omega_0 t) & 0 \\
\\
0 & 0 & 1
\end{array}
\right] [/math],
co prowadzi to ostatecznie do wyniku:
Wynik zaprezentowano na rysunku rys. 3.A.
Próbka umieszczona w polu statycznym, pobudzona polem zmiennym
Zakładamy, że pobudzenie prowadzi do powstania zjawiska rezonansu, to jest częstość impulsowego pola magnetycznego [math]\vec{B}_1[/math] jest równa częstości precesji Larmour'a. W takim, przypadku, w układzie rotującym występuje następująca konfiguracja pól magnetycznych:
- [math]\vec{B}_1 = B_1\vec{e}_x[/math],
- [math]\left[B_0 - \frac{\omega}{\gamma}\right]\vec{e}_x = 0[/math],
ponadto w równaniach Blocha możemy pominąć wyrazy związane z relaksacją, ponieważ czas trwania procesów relaksacyjnych (co najmniej kilkadziesiąt ms) jest znacznie dłuższy od trwania impulsu pobudzającego, co prowadzi ostatecznie do następującego układu równań:
przy następujących warunkach początkowych:
Rozwiązanie układu równań (Equation 62) ma postać:
gdzie: [math]\Omega = \gamma B_1[/math]. Rozwiązanie w układzie laboratoryjnym uzyskamy, po przemnożeniu równania (Equation 64) przez macierz obrotu [math]P[/math]:
co prowadzi do następującego równania na ewolucję magnetyzacji w układzie laboratoryjnym: Rozwiązanie układu równań (Equation 62) ma postać:
W układzie rotującym wektor namagnesowania wykonuje ruch precesyjny wokół kierunku pola pobudzającego [math]\vec{B}_1[/math], które w tym układzie zachowuje stały kierunek, podczas gdy w układzie laboratoryjnym, wektor magnetyzacji jest złożeniem dwóch ruchów precesyjnych:
- wokół statycznego pola [math]\vec{B}_0[/math],
- wokół rotującego w tym układzie pola [math]\vec{B}_1[/math].
Złożeniem tych dwóch ruchów precesyjnych jest spirala, symbolicznie zaprezentowano na rysunku rys. 3.B.
Wyłącznie impulsu pobudzającego. Sygnał swobodnej precesji
Po zmianie orientacji wektora namagnesowania o kąt [math]\frac{\pi}{2}[/math], w układzie rotującym leży on wzdłuż wzdłuż osi X' (jest równoległy do pola [math]\vec{B}_1[/math], zaś w układzie laboratoryjnym namagnesowanie rotuje w płaszczyźnie X-Y (patrz rys. 3.C). Dalsze utrzymywanie pobudzenia spowodowało by zmianę orientacji wektora namagnesowania a do jego ustawienia w kierunku przeciwnym do kierunku pola stałego [math]\vec{B}_0[/math]. Najdogodniejszy moment na pomiar wektora namagnesowania występuje w momencie, kiedy wiruje on w płaszczyźnie X-Y, w związku z czym impulsowe pole magnetyczne jest wyłączane i rozpoczynany jest pomiar magnetyzacji. Pomiar ten wykonywany jest za pomocą cewek i opiera się na zjawisku indukcji Faraday'a — zmienny strumień pola magnetycznego, wywołany przez rotujący w płaszczyźnie X-Y wektor namagnesowania indukuje w obwodzie siłę elektromotoryczną. Jednocześnie, po wyłączeniu pola pobudzającego, momenty magnetyczne zaczną powracać do w wyniku oddziaływań spin-sieć oraz spin-spin. Spowoduje zmianę orientacji wektora namagnesowania z płaszczyzny X-Y ponownie w kierunku pola statycznego [math]\vec{B}_0[/math]. Ewolucje wektora namagnesowania w takim przypadku możemy wyznaczyć przy pomocy równania Blocha, dla następującej konfiguracji pól magnetycznych w układzie rotującym:
- [math]\vec{B}_1 = 0\vec{e}_x[/math],
- [math]\left[B_0 - \frac{\omega}{\gamma}\right]\vec{e}_x = 0[/math],
otrzymując poniższy układ równań:
przy warunkach początkowych
Rozwiązanie układu równań (Equation 67) ma postać:
gdzie: [math]\omega_1 = \gamma B_1[/math]. Rozwiązanie w układzie laboratoryjnym uzyskamy, po przemnożeniu równania (Equation 69) przez macierz obrotu [math]P[/math]:
Ostatecznie, wektor namagnesowania ma postać:
Jak widzimy, namagnesowanie poprzeczne (składowa X oraz Y magnetyzacji) rotują w płaszczyźnie X-Y, jednocześnie zmniejszając swoją amplitudę na skutek procesów relaksacji. Cewki dokonujące pomiaru zarejestrują sygnał o przebiegu gasnącej sinusoidy. Sygnał ten pełni niezwykle ważną role i jest nazywany sygnałem swobodnej precesji (ang. Free Induction Decay, FID).
Echo spinowe
Czasy relaksacji zależą od właściwości fizyko-chemicznych tkanek. Stanowią zatem niezwykle cenna informację dla diagnostyki medycznej. Relaksacja spin-sieć zależy głównie od czynników "naturalnych" — fluktuacji lokalnych pół magnetycznych wytworzonych przez otoczenie jąder atomowych. Relaksacja spin-spin zależy zarówno od czynników naturalnych jak i "sztucznych" — niejednorodności statycznego pola magnetycznego związanych np. z ograniczoną dokładnością wykonania skanera MRI. W efekcie, zamiast obserwować zanik namagnesowania poprzecznego z czasem [math]T_{2}[/math], obserwujemy ten zanik z czasem:
Mimo to, możliwe jest wyznaczenie czasu relaksacji [math]T_{2}[/math], dzięki pięknemu zjawisku echa spinowego. U podstaw tego zjawiska leży założenie, iż naturalne procesy wpływające na relaksację spin-spin są procesami termodynamicznymi, natomiast procesy "sztuczne" są dobrze określone w czasie.
Kodowanie Obrazu
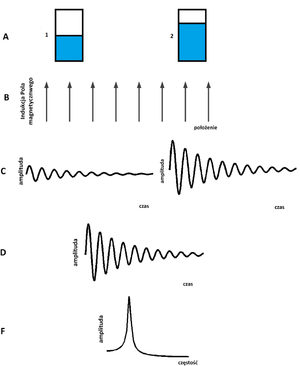
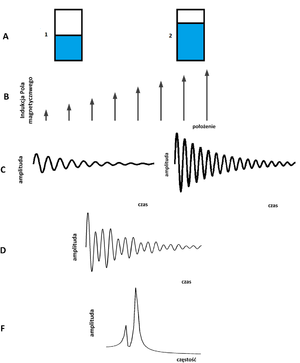
W jaki sposób jednak za pomocą MRI można otrzymać obraz, np. wnętrza ciała ludzkiego? Dotychczas zdobyta przez nas wiedza umożliwia nam pomiar magnetyzacji wytworzonej w badanej próbce, jednak nie potrafimy określić współrzędnych pewnej objętości materii, gdzie to namagnesowanie zostało wytworzone. Jak wiemy z poprzednich rozdziałów, namagnesowanie to wypadkowy moment magnetyczny pewnej objętości materii, który nazywamy wokselem. Cewka rejestruje zbiorczy sygnał pochodzący od wielu wokseli. W chwili wyłączenia impulsu pobudzającego [math]\frac{\pi}{2}[/math], ewolucję wektora namagnesowania opisuje następujący wzór:
gdzie: [math]A[/math] jest pewną stałą zależną od geometrii cewek, zaś [math]M^{0}(\vec{r})[/math] jest namagnesowaniem woksela, o objętości [math]dx\cdot dy\cdot dz[/math], którego pozycja jest opisana wektorem [math]\vec{r} = [x,y,z][/math] w kartezjańskim układzie współrzędnych. Zbiorczy sygnał rejestrowany przez cewkę odbiorczą wynosi z objętości [math]V[/math]:
Rozwiązanie tego problemu podali niezależnie Paul Lauterbur [3] oraz Peter Mansfield [4]. W roku 2003 obydwaj naukowcy zostali uhonorowani nagrodą Nobla w dziedzinie medycyny za wykorzystanie Magnetycznego Rezonansu Jądrowego w tej dziedzinie. W roku 1972 Paul Lauterbur przeprowadził doświadczenie, w którym wykazał, że przy wykorzystaniu gradientu dodatkowego pola magnetycznego możliwe jest rozróżnienie rejestrowanych sygnałów przez cewki, pochodzących od dwóch różnych próbek z wodą. Ideę eksperymentu zaprezentowano na No reference identifier provided i rys. 6. Jak widzimy, w celu określenia pozycji woksela, z którego mierzony jest dany sygnał FID niezbędne jest wprowadzenie dodatkowego, gradientowego pola magnetycznego:
gdzie:
[math]\vec{G} = [G_x,G_y,G_z][/math] - gradient indukcji pola magnetycznego.
W zależności od położenia woksela, częstość precesji momentów magnetycznych w zmodyfikowanym polu będzie wynosić:
Przyjęto, że proces określania współrzędnych wokseli z których rejestrowany jest sygnał FID, nazywany będzie kodowaniem. Proces ten składa się z trzech etapów: wyboru warstwy obrazowania, kodowania fazy i kodowania częstości, które opisane w kolejnych rozdziałach.
Etap wyboru warstwy
Wprowadzając zależność statycznego pola magnetycznego od położenia, można wyznaczać jedną ze współrzędnych woksela, w którym powstało namagnesowanie, wykorzystując w tym celu częstości sygnału FID. Przyjmijmy, że tą współrzędną będzie współrzędna [math]z[/math]:
gdzie:
- [math]B_{0}[/math] — statyczne pole magnetyczne, skierowane wzdłuż osi [math]z[/math],
- [math]G_{zz}[/math] — gradient pola magnetycznego, nałożony na pole [math]B_{0}[/math], [math]G_{zz} = \frac{\Delta B_{0}}{\Delta z}[/math].
Naświetlając badany obiekt polem elektromagnetycznym o częstości [math]\omega_{RF}[/math], wzbudzimy jądra atomowe w tych wokselach, w których spełniony jest warunek rezonansowy ([math]\omega_{RF} = \omega_{0}[/math]), czyli w wokselach, których współrzędna [math]z[/math] wyraża się wzorem (Equation 77). Opisana powyżej procedurę rzeczywiście stosuje się w MRI i określa jako etap wyboru warstwy (Slice selection), a gradient [math]G_{zz}[/math] {gradientem wyboru warstwy. Grubość wybranej w trakcie badania warstwy wynosi:
gdzie: [math]\Delta\omega[/math] — szerokość widmowa pobudzającego jądra impulsu radiowego. W przypadku, gdy impuls radiowy ma charakter sygnału prostokątnego o szerokości widmowej [math]\Delta\omega=4\pi/T[/math], gdzie: [math]T[/math] to długość trwania impulsu, grubość warstwy wyraża się poniższym wzorem:
- [math] \Delta z = \frac{4\pi}{\gamma G_{zz}T} [/math]
Etap kodowania fazy
W trakcie etapu wyboru warstwy, zaraz po włączeniu pola gradientowego wzdłuż osi [math]z[/math], włączany jest również impuls pobudzający [math]RF[/math], (najczęściej impuls [math]\pi/2[/math]). Po wyłączeniu tego impulsu oraz impulsu gradientowego [math]G_{zz}[/math] następuje precesja wektora magnetyzacji w płaszczyźnie [math]x-y[/math] z częstością [math]w_{0} = \gamma B_{0}[/math]. Załóżmy na początku, iż procesy relaksacji możemy pominąć. W praktyce wpływ procesów relaksacji typu spin-sieć na lokalizację woksela jest do pominięcia. Przypominamy, że relaksacja ta następuje z czasem [math]T_{1}[/math] rzędu kilkuset milisekund, podczas gdy wzbudzanie jąder osiąga się już po kilkuset mikrosekundach. Nie można natomiast pominąć procesów związanych z relaksacją typu spin-spin, których czas [math]T^{*}_{2}[/math] wynosi kilka-, kilkanaście milisekund.
Natychmiast po wyłączeniu pola gradientowego [math]G_{zz}[/math] włączane jest pole gradientowe [math]G_{yz}[/math] — tzw. gradient kodowania fazy, wzdłuż osi [math]y[/math]. Częstość precesji po włączeniu tego pola wynosi:
Włączenie gradientu [math]G_{yz}[/math] powoduje zróżnicowanie częstości precesji wektora magnetyzacji. Po wyłączeniu gradientu kodowania fazy po czasie [math]T_{y}[/math], fazy częstość precesji Larmour wraca do wartości [math]\omega_{0} = \gamma B_{0}[/math], jednakże pomiędzy rotującymi wektorami magnetyzacji pojawia się przesunięcie w fazie, które wyraża się następującym wzorem:
Rozdzielczość obrazu tomograficznego wzdłuż osi [math]y[/math] wynosi:
Etap kodowania częstości i odczyt pomiaru magnetyzacji
Po wyłączeniu gradientu [math]G_{yz}[/math], natychmiast włączany jest gradient [math]G_{xz}[/math] wzdłuż osi [math]x[/math], nazywany gradientem kodowania częstości oraz jednocześnie następuje odczyt sygnału FID. W wyniku przyłożenia gradientu [math]G_{xz}[/math] następuje zróżnicowanie częstości precesji wektora magnetyzacji, zgodnie z poniższym wzorem:
Podsumowując, w celu wybrania obszaru, w którym zostanie dokonany pomiar magnetyzacji, przeprowadzane są następujące kroki:
- Włączone zostaje statyczne pole magnetyczne [math]B_{0}[/math] wzdłuż osi Z. Wektory magnetyzacji wykonują ruch precesyjny wokół tej osi.
- Włączony zostaje gradient pola magnetycznego [math]G_{zz}[/math], po czym, po kilku milisekundach badany obiekt zostaje przez czas [math]t_{\pi/2}[/math] naświetlony falą elektromagnetyczną o określonej częstości. W warstwie, dla której zostaje spełniony warunek rezonansu, fala elektromagnetyczna wzbudza jądra atomowe, w wyniku czego wektory magnetyzacji wykonują ruch precesyjny w płaszczyźnie X-Y.
- Po wyłączeniu gradientu [math]G_{zz}[/math] zostaje włączony na okres [math]T_{yz}[/math] gradient kodowania fazy. Po jego wyłączeniu,wektory magnetyzacji wzdłuż osi Y precesują z tą samą częstością lecz w różnej fazie.
- Po wyłączeniu gradientu [math]G_{yz}[/math] zostaje włączony gradient kodowania częstości, który różnicuje częstość precesji wektora magnetyzacji. Jednocześnie następuje pomiar magnetyzacji (sygnału FID) w płaszczyźnie X-Y.
Podsumowując: gradient [math]G_{zz}[/math] wraz z impulsem pobudzającym umożliwiają zakodowanie współrzędnej Z wokseli, z których chcemy dokonać pomiaru namagnesowania obiektu. Jest to tzw. wybór warstwy gdzie będzie dokonywany pomiar. W następnych dwóch etapach zakodowany zostają współrzędne X i Y poszczególnych wokseli za pomocą częstości precesji wektora magnetyzacji oraz fazy jego precesji. Innymi słowy, każdemu wokselowi, zostaje przyporządkowana jednoznacznie częstość precesji Larmour'a oraz faza tej precesji.
Dekodowanie obrazu
W poprzednim rozdziale omówiliśmy metodę jednoznacznego przypisania wokselowi o współrzędnych [math]x[/math], [math]y[/math] w warstwie o położeniu [math]z[/math], częstości i fazy początkowej precesji wektora magnetyzacji. Cewki, które służą do pomiaru wytworzonego namagnesowania, rejestrują sygnał pochodzący od wszystkich wokseli w danej warstwie. W trakcie drugiego i trzeciego etapu kodowania obrazu namagnesowanie w wokselu o współrzędnych [math]x[/math] i [math]y[/math] uzyskuje częstość precesji Larmour: [math] \omega_{0} = \gamma\left(B_{0} + G_{xz}x\right) [/math] oraz fazę tej precesji: [math] \phi = \gamma G_{yz}yT_{y} [/math] Mierzony sygnał rezonansowy pochodzący od danego woksela w płaszczyźnie [math]x-y[/math] można wyrazić w następujący sposób:
Będziemy w dalej zajmowali się problemem wyznaczenia rozkładu gęstości protonów w płaszczyźnie już wybranej warstwy o grubości [math]dz[/math], dlatego wprowadzimy stałą [math]B = A\cdot dz[/math].
gdzie [math]B[/math] jest pewną stałą zależną od grubości warstwy oraz geometrii cewek, zaś [math]M^{0}(\vec{r})[/math] jest początkowym namagnesowaniem poprzecznym, uzyskanym w wyniku pobudzenia jąder atomowych impulsem [math]RF[/math]. Podstawiając do powyższego równania wzory (Equation 80) i (Equation 82) otrzymujemy:
a zatem sygnał rezonansowy rejestrowany z całej warstwy o współrzędnej [math]z[/math] wynosi:
Otrzymane równanie porządkujemy w następujący sposób:
podstawiając:
uzyskujemy:
Wymiar stałej [math]B[/math] zawiera jednostkę długości (powiązaną z grubością warstwy), z kolei namagnesowanie to całkowity moment magnetyczny przypadający na jednostkę objętości [math]dV[/math]. Namagnesowanie woksela zależeć będzie od całkowitej liczby jąder atomowych znajdujących się w objętości [math]dV[/math]. W związku z tym, uwzględniając jednostkę stałej [math]B[/math] oraz namagnesowania [math]M^{0}[/math] możemy przepisać równanie (Equation 90) do następującej postaci:
gdzie [math]B'[/math] to stała zależna już tylko od właściwości cewek, natomiast [math]\rho^{0}_{xy}[/math] jest gęstością jąder atomowych w badanej warstwie. Widzimy zatem, iż mierzony sygnał jest transformatą Fouriera gęstości jąder atomowych, z dokładnością do wagi, zależnej od natężenia statycznego pola magnetycznego oraz czasu relaksacji [math]T_{2}[/math][5]. Rozkład gęstości jąder atomowych można wyznaczyć obliczając odwrotną transformatę Fouriera równania (Equation 90)
Podsumowując: Główną informacją jaką otrzymujemy za pomocą obrazowania metodą jądrowego rezonansu magnetycznego jest rozkład gęstości jąder atomowych. Z uwagi, iż jądro atomu wodoru ma największy spośród jąder atomowych współczynnik giromagnetyczny, a także ze względu na wysokie stężenie wodoru w organizmie ludzkim, za pomocą MRI uzyskuje się obraz rozkładu gęstości tego właśnie pierwiastka. W badaniu otrzymamy zatem bardzo dobry obraz tkanek miękkich (np. mózg), co odróżnia tą metodę od Rentgenowskiej Tomografii Komputerowej, najlepiej obrazującą kości. Ponadto, mierząc czasy relaksacji namagnesowania — [math]T_{1}[/math] i [math]T_{2}[/math] możliwe jest uzyskanie informacji o pewnych właściwościach fizyko-chemicznych tkanek.
Podstawowa Sekwencja Gradientów Pola Magnetycznego
W tym rozdziale dokonamy pewnego podsumowania dotychczas zdobytej wiedzy dotyczącej procesu kodowania i dekodowania obrazu w Magnetycznym Rezonansie Jądrowym. Podstawowa sekwencja kodująca oraz proces dekodowania został zaprezentowany na rys. ??? Z uwagi na ograniczoną ilość miejsca pod rysunkiem, jego opis znajdzie w treści rozdziału. Załóżmy, że chcemy zobrazować wybraną warstwę głowy pacjenta. Obraz zostanie utworzony za pomocą macierzy [math]M[/math]x[math]N[/math] pikseli. Proces obrazowania będzie składał się następujących kroków:
- Umieszczenia pacjenta w stałym polu magnetycznym o indukcji [math]B_0[/math]. Po wykonaniu tego kroku momenty magnetyczne jąder wykonują precesję z częstością [math]\omega_0 = \gamma B_0[/math]. Powstaje wypadkowe namagnesowanie [math]M_0[/math] w kierunku pola [math]\vec{B}_0[/math]. Załóżmy, że w głowie pacjenta znajdują się tylko dwa obszary dające znaczące sygnały. Obszary te wypełniona różnymi odcieniami szarości.
- Włączenia pola gradientowego w kierunku osi z (przyjęto, że jest to oś biegnąca wzdłuż badanego). Następuje zróżnicowanie precesji momentów magnetycznych protonów. Częstość precesji zależy teraz od współrzędnej z w następujący sposób: [math]\omega_{0} = \gamma\left(B_{0} + G_{zz}z\right)[/math]. Równocześnie wraz z gradientem pola zostaje włączony impuls pobudzający (RF) [math]\frac{\pi}{2}[/math] o częstości [math]\omega_1[/math]. Wywoła on pobudzenie tych momentów magnetycznych, których częstość precesji Larmoura wynosi [math]\omega = \omega_1[/math], czyli [math]\omega_1 = \gamma\left(B_{0} + G_{zz}z\right)[/math]. Są to momenty magnetyczne znajdujące się w płaszczyźnie x-y o współrzędnej z równej: [math]z = \frac{\left(\omega_{1} - \gamma B_{0}\right)}{\gamma G_{z}}[/math]. W wokselach leżących w wybranej warstwie następuje zmiana orientacji wektora namagnesowania [math]M_0[/math] o kąt [math]\frac{\pi}{2}[/math]. Warto zauważyć, iż po wyłączeniu tego pola gradientowego, momenty magnetyczne ponownie ruch precesyjny z częstością Larmoura [math]\omega=\gamma B_0[/math], jednak w odróżnieniu od wektorów leżących w innych warstwach maja one zmienioną orientację.
- Wzdłuż osi y zostaje włączone na pewien okres czasu kolejne pole gradientowe, którego wartość na rys. ??? oznaczono kolorem żółtym. Wektor magnetyzacji zaczynają rotację w płaszczyźnie x-y z różną prędkością (ale tą samą dla zadanej współrzędnej y). Po wyłączeniu pola gradientowego, częstość precesji wraca do wartości [math]\omega = \gamma B_0[/math], jednakże wektory namagnesowania wirują w płaszczyźnie x-y w różnej fazie.
- Następuje kolejne włączenie pola gradientowego, tym razem wzdłuż osi x. Momenty magnetyczne, a także namagnesowanie zaczyna wirować z różną częstością, zależną od współrzędnej x. Jednocześnie wraz z włączeniem tego gradientu następuje pomiar sygnału. Na tym etapie kodowania obrazu, można powiedzieć, że wektory namagnesowania znajdujące się w wokselach leżących w tej samej kolumnie (oś y) rotują z tą samą częstością, natomiast wektory namagnesowania, znajdujące się w tym samym wierszu (os x) rotują z tą samą fazą. Należy pamiętać, iż włączenie gradientu wzdłuż osi y w poprzednim etapie zmieniło jedynie fazę sygnału FID. Sygnały o tej samej częstości i różnej fazie nałożą się na siebie, dając pewien sygnał wypadkowy. Innymi słowy, na podstawie widma zarejestrowanego sygnału FID możliwe jest w tej chwili rozróżnienie z której kolumny pochodzą składowe mierzonego sygnału. Nie znamy natomiast współrzędnej y wokseli, z których pochodzi istotny sygnał. W związku z tym całość pomiaru (poczynając od etapu 2) należy powtórzyć, tyle razy, ile mamy wierszy w obrazie, za każdym razem zmieniając wartość gradientu pola magnetycznego wzdłuż osi y lub długość czasu jego trwania.
- Wartości Transformat Fouriera zapisywane są w tzw. współrzędnych przestrzeni K, tworząc pewną macierz. Wykonanie odwrotnej, dwuwymiarowej Transformaty Fouriera tej macierzy umożliwia wyznaczenie rozkładu przestrzennego namagnesowania.
Co obrazuje Magnetyczny Rezonans Jądrowy
Rozkład gęstości protonów
W trakcie badania MRI dokonywany jest pomiar namagnesowania małych jednostek objętości (wokseli) danego obszaru pacjenta. Namagnesowanie woksela jest proporcjonalne do liczby momentów magnetycznych cząstek znajdujących się w nim cząstek posiadających momenty magnetyczne. Spośród wielu atomów, które wchodzą w skład organizmu ludzkiego i posiadających spin, wodór charakteryzuje się największą abundancją oraz jądrem o największym momencie magnetycznym. MRI będzie zatem obrazował głownie rozkład gęstości wodoru. W przeciwieństwie do Metod Rentgenowskich, MRI będzie zatem bardzo dobrze obrazował tkanki miękkie.
Kontrast [math]T_{1}[/math] oraz [math]T_{2}[/math]
Bardzo ważną informację diagnostyczną można również uzyskać, wykorzystując do tego czas pomiaru relaksacji [math]T_1[/math] i [math]T_2[/math]. Relaksacja wektora namagnesowania następuje w wyniku oddziaływania momentów magnetycznych z otoczeniem. Na podstawie zmian w szybkości zaniku namagnesowania poprzecznego lub odbudowie namagnesowania podłużnego można zatem wyciągnąć pewne wnioski diagnostyczne. Dokonuje się tego przy pomocy odpowiednio dobranej sekwencji pola pobudzającego, którego skutkiem będzie lepsze uwidocznienie na obrazie obszarów o krótkim czasie [math]T_1[/math] lub krótkim czasie [math]T_2[/math]. Mówimy wtedy odpowiednio o obrazie T1 zależnym lub T2 zależnym, bądź kontraście T1 lub T2.
Obok rozkładu gęstości jąder atomu wodoru, za pomocą MRI możemy wyznaczyć również czasy relaksacji magnetyzacji podłużnej — [math]T_{1}[/math] oraz magnetyzacji poprzecznej — [math]T_{2}[/math]. Czasy te zależą od właściwości fizyko-chemicznych tkanek. Z dotychczasowych badań wiadomo, iż czasy relaksacji tkanki zdrowej, różnią się znacznie od czasów relaksacji tej samej tkanki chorej (np. rakowej). Czasy relaksacji zawierają zatem niezwykle cenna z punktu widzenia diagnostyki informacje.
Budowa skanera MRI
Cewki pola statycznego
Podstawowym elementem aparatury MRI są przyrządy wytwarzające pola magnetyczne (statyczne jak i gradientowe) oraz rejestrujące sygnał namagnesowania. Statyczne pole magnetyczne [math]\vec{B}_{0}[/math] można wygenerować za pomocą:
- Magnesów trwałych. Małe zużycie prądu elektrycznego, nieskomplikowana budowa aparatury, ogólnie niskie koszty obsługi. Skaner ma mniejsze rozmiary niż w przypadku skanerów w których pole magnetyczne jest wytwarzane w inny sposób, ponadto ma budowę otwartą (pacjent nie znajduje się w wąskim cylindrze), co zwiększa komfort badania (np. u pacjentów z klaustrofobią).
- Wady — trwałe magnesy są ciężkie, wytwarzają pola magnetyczne w granicy: 0.064 T - 0.3 T.
- Elektromagnesów. Pole magnetyczne powstaje w wyniku przepływu prądu przez cewkę. Elektromagnesy mogą mieć rdzeń powietrzny lub stalowy. Zalety — otwarta budowa zwiększająca komfort badania, można wyłączyć skaner, jeśli jest nieużywany, niska cena skanera.
- Wady — wysokie zużycie energii elektrycznej, ograniczone wartość wytwarzanego pola magnetycznego < 0.2 - 0.3T, potrzebne chłodzenie wodne, wytworzone pole magnetyczne "rozprzestrzenia" się na boki.
- Magnesów nadprzewodzących — najczęściej stosowane. Pole magnetyczne wytwarzane jest przez przepływ prądu w cewkach umieszczonych w ciekłym helu, w celu redukcji zjawiska oporu elektrycznego — W temperaturze 4 Kelvinów (-269[math]^{o}[/math]) opór ten zanika.
- Zalety — możliwość generowania silnych, bardzo jednorodnych pól magnetycznych — do 12T, a co za tym idzie możliwość rejestracji sygnału namagnesowania o wysokim SNR oraz skrócenie czasu wykonywania skanu. Ponadto niskie zużycie prądu elektrycznego.
- Wady — drogi skaner, wysokie koszty związane z obsługą aparatury kriogenicznej, aparatura hałaśliwa i o zwartej budowie — mniejszy standard wygody dla pacjenta, wrażliwszy na artefakty ruchowe, skomplikowana budowa (cewki nadprzewodzące muszą być zabezpieczone wieloma warstwami termicznymi, oraz przestrzeniami próżniowymi, aby chronić Hel przed zagotowaniem się i eksplozją).
Cewki nadawczo odbiorcze
Źródłem sygnału pobudzającego jądra atomowe w zjawisku jądrowego rezonansu magnetycznego, jak i odbiornikiem rejestrującym wytworzony sygnał namagnesowania są tzw. Cewki RF. Istnieje wiele różnorodnych typów cewek, przeznaczonych do określonych badań, można je jednak podzielić na dwie grupy:
- Cewki objętościowe. Wewnątrz takiej cewki wytworzone zostaje jednolite pole magnetyczne, wymagają jednak, aby badana część pacjenta znajdowała się w środku cewki.
- Cewki powierzchniowe. Jak sama nazwa wskazuje cewki takie umieszczane są na powierzchni, blisko obszaru, który ma być badany. Cewki takie zapewniają sygnał o wysokim SNR oraz wysoką rozdzielczość otrzymywanych obrazów. Wada tych cewek jest szybka strata jednolitości otrzymywanego obrazu, w przypadku gdy badany obiekt przemieści się poza cewkę.
Podstawy kwantowego opisu zjawiska Rezonansu Magnetycznego
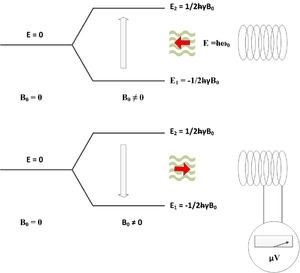
Podstawowy opis kwantowy zjawiska rezonansu magnetycznego przeprowadzimy dla protonu. Przypominamy, własny moment pędu protonu opisywany jest spinową liczbą kwantową [math]I = \frac{1}{2}[/math], długość wektora momentu pędu wynosi [math]|\vec{I}| = \frac{\sqrt{3}}{2}\hbar [/math], zaś rzut wektora spinu na oś Z może przyjmować wartości: [math]\vec{I}_{z} = \pm\frac{1}{2}\hbar [/math]. Pod nieobecność zewnętrznego pola magnetycznego, rzutom wektora spinu proton una oś Z odpowiadają stany o tej samej energii.
Wprowadzenie próbki w stałe pola magnetyczne o wartości [math]B_0[/math] i kierunku równoległego do osi X powoduje rozczepienie tych stanów. Rzut wektora momentu magnetycznego (związanego ze spinem) na oś Z może mieć kierunek równoległy lub przeciwny do kierunku pola magnetycznego. Rzutom tym odpowiadają dwa poziomy energetyczne:
gdzie: [math]E_1, E_2[/math] to odpowiednio energia stanu związanego z równoległym i przeciwnym rzutem momentu magnetycznego na kierunek stałego pola magnetycznego. Zgodnie z zasadami termodynamiki, protony będą dążyły do zajmowania stanów o niższej energii. Dostarczając dodatkową energię, np. za pomocą fali elektromagnetycznej, można doprowadzić do przejścia protonów ze stanu podstawowego do wzbudzonego. Częstość fali elektromagnetycznej można wyliczyć w następujący sposób. Różnica energii pomiędzy dwoma stanami wynosi:
Fala elektromagnetyczna o częstości [math]\omega_0[/math] posiada energię:
Energia fali elektromagnetycznej powinna być równa różnicy energii dwóch stanów kwantowych:
ostatecznie, częstość fali wzbudzającej przejścia pomiędzy poziomami energetycznymi jest równa:
Po wyłączeniu fali pobudzającej, protony przechodzą ze stanu wzbudzonego do stanu podstawowego, emitując nadmiar energii. Pobudzeniowa fala elektromagnetyczna może być wygenerowana za pomocą cewki, która po wyłączeniu emisji fali może również rejestrować energię emitowaną przez protony przechodzące do stanu podstawowego. Bardziej rozszerzony (nieobowiązkowy dla studentów opis zjawiska magnetycznego rezonansu jądrowego można znaleźć w kolejnym rozdziale).
Kwantowy opis zjawiska Rezonansu Magnetycznego
Zastosowanie modelu kwantowego prowadzi do pełniejszego w porównaniu z modelem klasycznym opisu zjawiska NMR, jednak ze względu na skomplikowaną postać samej Teorii Kwantów, model kwantowy może być trudny w zrozumieniu. Z kolei model klasyczno-kwantowy (zaprezentowany w dotychczasowych rozdziałach), jest łatwiejszy do przyswojenia i dla pewnej klasy problemów uzyskuje się za jego pomocą te same wyniki co w modelu kwantowym.
Nim przejdziemy do szczegółowego opisu zjawiska NMR, dokonamy zestawienia niektórych z postulatów leżących u podstaw Mechaniki Kwantowej i Klasycznej oraz przypomnimy sobie znaczenie pewnych pojęć stosowanych w fizyce.
- Układem fizycznym (w dalszej części skryptu nazywanym w skrócie układem) określa się zbiór ciał.
- Stan układu jest najmniejszym zbiorem informacji pozwalającym odpowiedzieć na wszelkie pytania dotyczące układu.
- W Mechanice Klasycznej pomiar wielkości fizycznej można wykonać z dokładnością ograniczoną jedynie precyzją dostępnej aparatury. Sam pomiar nie wpływa na układ.
-
W Mechanice Kwantowej nie można dokonać jednoczesnego pomiaru pewnych wielkości fizycznych z dowolną dokładnością. Ograniczenie to, znane jako Zasada Nieoznaczoności Heisenberga, nie ma nic wspólnego z precyzja aparatury pomiarowej. Jest to jedno z praw przyrody, któremu podlegają np. pomiary położenia i pędu:
- [math] \Delta x\Delta p_{x}\ge \hbar [/math]
- [math]\Delta x[/math] i [math]\Delta p_x[/math] to odpowiednio nieoznaczoność położenia i pędu wzdłuż osi [math]x[/math]
pomiary energii i czasu:
- [math] \Delta E\Delta t\ge \hbar [/math]
gdzie:
- [math]\Delta E[/math] i [math]\Delta t[/math] to odpowiednio nieoznaczoność energii i czasu.
pomiary składowych wektora momentu pędu (w Mechanice Kwantowej obserwowalna jest w danym pomiarze tylko jedna ze składowych wektora oraz jego długość). Możliwy jest natomiast jednoczesny pomiar z dowolną dokładnością np. energii i pędu. Warto zauważyć, że chociaż nie da się, zgodnie z Zasadą Nieoznaczoności, jednocześnie zmierzyć np. położenia i pędu cząstki, to można wyznaczyć osobno rozkład prawdopodobieństwa dla pędów i rozkład prawdopodobieństw dla położeń w danym stanie układu. Mierząc dostatecznie dużo takich rozkładów prawdopodobieństwa, można określić stan układu. Pojedynczą wielkość da się w zasadzie zmierzyć z dowolną dokładnością, ale jeżeli mamy kilka takich samych układów w tym samym stanie, to na ogół dla każdego z nich pomiar tej wielkości da inny wynik.
- W Mechanice Klasycznej położenie, orientacja oraz wielkości charakteryzujące ruch układu w danej chwili określają stan układu w tej chwili. W przypadku cząstki punktowej do określenia jej stanu w przestrzeni trójwymiarowej wystarczy sześć wielkości jednowymiarowych: 3 współrzędne opisujące położenie cząstki oraz 3 wielkości charakteryzujące jej ruch (prędkość lub pęd).
- W Mechanice Kwantowej stan układu określony jest za pomocą funkcji falowej [math]\psi \left(\vec{r},t\right)[/math]. Funkcja falowa zawiera pełną informacje o stanie układu. Zwykle jednak nie da się przewidzieć wyniku pomiaru znając nawet dokładnie stan układu.
- Interpretacja fizyczna funkcji falowej jest następująca (cyt. z pracy [6]) Funkcja falowa [math]\psi \left(\vec{r},t\right)[/math] opisuje fale prawdopodobieństwa. Wielkość [math]\psi ^{*}\left(\vec{r},t\right)\psi \left(\vec{r},t\right)[/math] jest gęstością prawdopodobieństwa znalezienia cząstki w punkcie [math]\vec{r}[/math] w chwili [math]t[/math]. Inaczej mówiąc, całka: [math]P_{D}\left(t\right)=\int _{D}d^{3}\vec{r}\left|\psi \left(\vec{r},t\right)\right|^{2}[/math] jest prawdopodobieństwem znalezienia cząstki w chwili [math]t[/math] w obszarze [math]D[/math].
- Funkcja falowa musi spełniać warunek unormowania[7]: [math]\int _{D}d^{3}\vec{r}\left|\psi \left(\vec{r},t\right)\right|^2 = 1[/math]. Innymi słowy, prawdopodobieństwo znalezienia cząstki w dowolnym punkcie przestrzeni jest równe jedności.
- W Mechanice Klasycznej pomiar wielkości fizycznej nie wpływa na układ.
- W Mechanice Kwantowej zwykle nie można gwarantować, że stan układu po pomiarze będzie taki sam jak przed pomiarem. W szczególności ponowny pomiar wielkości, która przedtem była dobrze określona, może dać (zupełnie) inny wynik.
-
W Mechanice Kwantowej dowolnej, dobrze określonej obserwabli fizycznej (takiej jak pęd, energia, masa czy moment pędu), dalej oznaczanej przez [math]C[/math], odpowiada operator [math]\hat{C}[/math] taki, że w wyniku pomiaru obserwabli [math]C[/math] otrzymujemy wartości zmierzone [math]c[/math], które są wartościami własnymi operatora [math]\hat{C}[/math]:
- [math] \hat{C}\phi = c\phi [/math]
-
W Mechanice Kwantowej, jeśli układ znajduje się w stanie [math]\psi \left(\vec{r},t\right)[/math], to średnia wartość dowolnej obserwabli fizycznej [math]C[/math] związanej z układem w chwili czasu [math]t[/math] dana jest wzorem:
[math] \left\lt C\right\gt = \int \psi ^{*}\left(\vec{r},t\right)\hat{C}\psi \left(\vec{r},t\right)d^{3}\vec{r} [/math]
Spin
Dokładny opis spinu, który jest wielkością kwantową, wykracza znacznie poza ramy materiału niniejszego skryptu. Zainteresowanych czytelników odsyłamy do prac [6], [8], [9], na podstawie których został napisany niniejszy rozdział. W tym miejscu natomiast ograniczymy się do podania kilku faktów, obserwacji, czy uwag, mając nadzieję, że wystarczą one czytelnikom do zrozumienia, czym jest spin, przynajmniej w takim stopniu, który ułatwi im przyswojenie wiadomości na temat Jądrowego Rezonansu Magnetycznego. Podstawowymi elementami, z których składa się materia, są cząstki takie jak elektron, proton oraz neutron, które posiadają spin równy [math]\frac{1}{2}[/math]. Najbardziej rozpowszechnionym pierwiastkiem w organizmach żywych jest wodór, którego jądra — protony, odgrywają podstawową rolę w otrzymywaniu obrazów MR. W związku z tym omówienie pojęcia spinu ograniczymy do przypadku spinu równego [math]\frac{1}{2}[/math].
- Zjawiska takie jak rozszczepienie w niejednorodnym polu magnetycznym wiązki atomowej na dwie składowe, zaobserwowane przez Sterna i Gerlacha w roku 1922, czy dubletowa struktura widm pierwiastków alkalicznych nie zostały wyjaśnione w ramach teorii budowy atomu zaproponowanej przez Bohra. Doświadczenie przeprowadzone przez Sterna i Gerlacha, jak również i badania spektroskopowe wskazywały na nie uwzględnienie w teorii Bohra pewnej wielkości fizycznej — nieznanego, dodatkowego stopnia swobody elektronu.
- W roku 1925 Uhlenbeck i Goudsmit wprowadzają pojecie spinu, jako wewnętrznego momentu pędu elektronu. Uhlenbeck i Goudsmit przyjęli, iż elektron wiruje[10] wokół własnej osi, co w naturalny sposób umożliwiło im wytłumaczenie istnienia dodatkowego stopnia swobody oraz wyjaśnienie dubletowej struktury widm pierwiastków alkalicznych. Obecnie wiadomo, iż obraz elektronu jako wirującej kulki zaproponowany przez Uhlenbecka i Goudsmita jest nieprawidłowy.
-
W roku 1926 Schrödinger publikuje serię czterech prac dotyczących równania falowego (nazwanego później równaniem Schrödingera), które dla elektronu znajdującego się w polu elektromagnetycznym przyjmuje następującą postać [6]:
[math] i\hbar\frac{\partial \psi \left(\vec{r},t\right)}{\partial t} = \left[ \frac{1}{2m} \left(\frac{\hbar }{i} \nabla - e \vec{A}\right)^2 + e \phi (\vec{r}) \right]\psi \left(\vec{r},t\right) [/math]
gdzie:
- [math]\vec{B} = \nabla \times \vec{A}[/math]
- [math]\vec{E} = -\nabla \phi - \frac{\Delta \vec{A}}{\Delta t}[/math]
- [math]\vec{B}[/math] to wektor indukcji magnetycznej
- [math]\vec{E}[/math] to wektor natężenia pola elektrycznego
- Rozwiązaniem równania (%i 150) są funkcje skalarne, które jednak nie opisują właściwie zachowania się elektronu w polu magnetycznym.
- W przyrodzie obserwujemy zarówno fale skalarne (np. fale dźwiękowe) jak i fale wektorowe (np. fale elektromagnetyczne). Fale wektorowe mogą ulegać polaryzacji. Doświadczenie Sterna-Gerlacha wskazuje na to, że również fale prawdopodobieństwa mogą zostać spolaryzowane, zaś pole magnetyczne inaczej wpływa na poszczególne składowe polaryzacyjne [6].
-
Najprostszym sposobem wprowadzenia oddziaływania zależnego od pola magnetycznego i polaryzacji funkcji falowej do równania Schrödingera, jest przedstawienie go w postaci następującego układu równań [6]:
[math] \begin{array}{l} i \hbar \frac{\partial \psi _{+}\left(\vec{r},t\right)}{\partial t} = \left[\frac{1}{2m}\left( \frac{\hbar }{i}\nabla - e \vec{A}\right)^{2} + e \phi - \mu B \right] \psi _{+}\left(\vec{r},t\right) \\ \\ i \hbar \frac{\partial \psi _{-}\left(\vec{r},t\right)}{\partial t} = \left[\frac{1}{2m}\left( \frac{\hbar }{i}\nabla - e \vec{A}\right)^{2} + e \phi + \mu B \right] \psi _{-}\left(\vec{r},t\right) \end{array} [/math]
- Funkcja falowa cząstki posiadającej spin powinna zależeć nie tylko do zmiennych przestrzennych, ale również od dyskretnej zmiennej spinowej, opisującej wartość rzutu spinu na dowolnie wybraną w przestrzeni oś. Funkcja taka, oznaczmy ją dalej przez [math]\psi \left(\vec{r},t,m_{s}\right)[/math], będzie zbiorem różnych funkcji numerowanych przez parametr [math]m_{s}[/math] związany ze spinem. Operator spinu działając na funkcję falową, będzie działał jedynie na składowe spinowe.
-
Równanie (%i 100) nie jest dogodną formą opisu oddziaływania pola magnetycznego ze spolaryzowaną falą prawdopodobieństwa. W roku 1927 Pauli pokazał, jak z dwóch funkcji falowych, przypisanych dwóm stanom polaryzacyjnym cząstki zbudować wielkość wektorową. Pomijając skomplikowane przekształcenia matematyczne, podamy rozwiązanie do którego doszedł Pauli. Z dwóch składowych polaryzacyjnych funkcji falowej: [math]\psi \left(\vec{r},t\right)_{+}[/math] i [math]\psi \left(\vec{r},t\right)_{-}[/math], można zbudować dwuwymiarowy wektor i wektor do niego sprzężony:
[math] \begin{array}{l} \psi \left(\vec{r},t\right) = \left[ \begin{array}{l} \psi _{+}\left(\vec{r},t\right) \\ \\ \psi _{-}\left(\vec{r},t\right) \end{array} \right]\\ \\ \psi ^{*}\left(\vec{r},t\right) = \left[ \psi ^{*}_{+}\left(\vec{r},t\right), \psi ^{*}_{-}\left(\vec{r},t\right) \right] \end{array} [/math]
który spełnia następujące równanie falowe:
[math] i \hbar \frac{\partial \psi \left(\vec{r},t\right)}{\partial t} = \left[ \frac{1}{2m} \left( \frac{\hbar }{i}\nabla - e \vec{A}\right)^{2} + e \phi (\vec{r}) - \mu \vec{B} \vec{\sigma } \right] \psi \left(\vec{r},t\right) [/math]gdzie:
- [math]\vec{B}[/math] jest indukcją pola magnetycznego, zaś [math]\vec{\sigma }[/math] jest wektorem zbudowanym z tzw. macierzy Pauliego [math]\sigma _{x}[/math], [math]\sigma _{y}[/math], [math]\sigma _{z}[/math]:
[math] \vec{\sigma }=\left[\mathbf {\sigma }_{x},\mathbf {\sigma }_{y},\mathbf {\sigma }_{z}\right] [/math][math] \begin{array}{l} \sigma _{x} = \left[ \begin{array}{cc} 0 & 1\\ 1 & 0 \end{array} \right]\\ \\ \sigma _{y} = \left[ \begin{array}{cc} 0 & -i\\ i & 0 \end{array} \right]\\ \\ \sigma _{z} = \left[ \begin{array}{cc} 1 & 0\\ 0 & -1 \end{array} \right] \end{array} [/math]Iloczyn wektora [math]\vec{\sigma }[/math] oraz wektora [math]\vec{B}[/math] wynosi:
[math] \vec{B}\vec{\sigma } = \left[ \begin{array}{cc} B_{z} & B_{x} - iB_{y}\\ \\ B_{x} + iB_{y} & -B_{z} \end{array} \right] [/math]
- W roku 1928 Dirac podał równanie falowe dla relatywistycznej cząstki o spinie [math]\frac{1}{2}[/math] poruszającej się w polu elektromagnetycznym. Rozwiązanie równania Diraca dla elektronu doprowadziło do wniosku, że spin jest składową całkowitego momentu pędu cząstki, wnosząc do niego wkład równy [math]\frac{1}{2}\hbar [/math]. Równanie Diraca przewiduje istnienie spinu jako efektu relatywistycznego.
-
Operatory składowych wektora spinu są następujące [2]:
[math] \begin{array} {l} \hat{s}_{x} = \frac{\hbar }{2} \left[ \begin{array}{cc} 0 & 1\\ 1 & 0 \end{array} \right]\\ \\ \hat{s}_{y} = \frac{\hbar }{2} \left[ \begin{array}{cc} 0 & -i\\ i & 0 \end{array} \right]\\ \\ \hat{s}_{z} = \frac{\hbar }{2} \left[ \begin{array}{cc} 1 & 0\\ 0 & -1 \end{array} \right] \end{array} [/math]
a zatem operator spinu jest równy:
[math] \hat{S} = \frac{1}{2}\hbar \vec{\sigma } [/math]
Podsumowując, spin należy rozumieć w ramach Mechaniki Kwantowej jako wyraz istnienia stanów polaryzacyjnych funkcji falowej (w przypadku elektronu, protonu, neutronu i niektórych jąder będą to dwa stany polaryzacyjne). Spin jest własnością cząstek, taką samą jak np. masa lub ładunek, ale obserwowalną dopiero w eksperymentach ujawniających kwantową naturę materii. Spin jest także składową całkowitego momentu pędu, niezwiązaną z ruchem, można go zatem również interpretować jako własny (wewnętrzny) moment pędu cząstki.
Spin i moment magnetyczny jądra atomowego
Jądra atomowe zawierające nieparzystą liczbę protonów lub neutronów mają niezerowy własny moment pędu [math]\vec{I}[/math] (spin) oraz związany z nim moment magnetyczny. Zgodnie z regułami opisu wielkości wektorowych w mechanice kwantowej, jednocześnie może być obserwowalna tylko długość wektora oraz wartość jednej z jego składowych (tzw. rzut tego wektora na wyróżnioną oś, nazywaną osią kwantowania). W przypadku wektora własnego momentu pędu jądra atomowego jego długość wynosi [2]:
gdzie:
- [math]I[/math] oznacza liczbą kwantową o wartości całkowitej lub połówkowej.
Składowa [math]z[/math] momentu pędu wyraża się następującym wzorem [2]:
Możliwych jest zatem [math]2I+1[/math] orientacji spinu jądra względem wyróżnionego kierunku, odpowiadających możliwym wartościom jądrowej magnetycznej liczby kwantowej [math]m_{I}[/math]. W przypadku protonu (jądra atomu wodoru), mamy [2]:
- [math] \begin{array}{l} I=1/2\\ \\ |\vec{I}| = \frac{\sqrt{3}}{2}\hbar \\ \\ (\vec{I})_{z} = \pm \frac{1}{2}\hbar \end{array} [/math]
Moment magnetyczny związany jest ze spinem następującą zależnością [2]:
Energia potencjalna oddziaływania momentu magnetycznego z polem magnetycznym wynosi:
Zgodnie z prawami termodynamiki układ fizyczny dąży do stanu, w którym jego energia wewnętrzna osiągnie wartość minimalną. Rozważmy pole [math]\vec{B}[/math], posiadające tylko składową wzdłuż osi [math]z[/math] (czyli [math]\vec{B}_0 = \left[ 0, 0, B_0\right][/math]), układu odniesienia. W przypadku protonu, posiadającego ładunek dodatni, kierunek momentu magnetycznego jest zgodny z kierunkiem jego własnego momentu pędu, a zatem również rzuty momentu magnetycznego i momentu pędu na oś [math]z[/math] są równoległe. Orientacji momentu pędu zgodnej z kierunkiem pola [math]\vec{B}[/math] będzie odpowiadać energia potencjalna:
- [math] V = -\frac{1}{2}\hbar \gamma B_0 [/math]
natomiast orientacji antyrównoległej:
- [math] V = \frac{1}{2}\hbar \gamma B_0 [/math]
Ustawienie najkorzystniejsze energetycznie odpowiada więc sytuacji, kiedy składowa [math]z[/math] spinu ustawiona jest w równolegle do kierunku pola [math]\vec{B}_0[/math] (magnetyczna liczba kwantowa [math]m_{I}=\frac{1}{2}[/math]).
Precesja spinu i momentu magnetycznego w stałym polu magnetycznym — opis kwantowy dla cząstki o spinie 1/2
Ze względu na wysokie naturalne rozpowszechnienie wodoru w organizmach żywych, oddziaływanie spinu z polem magnetycznym omówimy na przykładzie protonu. Dodatkowo, aby uprościć problem, rozważmy proton mający stałe położenie w przestrzeni oraz pole magnetyczne [math]\vec{B}_{0}[/math], które ma niezerową składową tylko wzdłuż osi [math]z[/math], czyli [math]\vec{B}=\left[0, 0, B_{0}\right][/math]. W takim przypadku równanie Pauliego przybierze następującą postać:
Powyższe równanie można rozwiązać metodą rozdzielenia zmiennych przestrzennych i spinowych [6]:
gdzie:
- [math]\psi _{r}\left(\vec{r},t\right)[/math] — zależy wyłącznie od współrzędnych przestrzennych i czasu
- [math]\chi \left(t\right)[/math] — jest dwuskładnikowym spinorem.
w wyniku podstawienia równania (%i 113) do równania (%i 112) uzyskujemy następujący układ dwóch niezależnych równań:
Interesuje nas ewolucja spinu, dlatego rozwiążemy dalej tylko równanie dla funkcji [math]\chi \left(t\right)[/math]. Podstawiając:
do równania (%i 114), otrzymujemy:
Jest to układ równań różniczkowych rzędu pierwszego o rozwiązaniach postaci:
Dokonajmy analizy jednostkowej uzyskanego rozwiązania. Argument funkcji wykładniczej powinien być bezwymiarowy. Wielkość [math]\mu B_{0}[/math] ma wymiar energii, z kolei stała Planka ma wymiar [math]\left[\textrm {Js}\right][/math], a zatem:
- [math] \pm i\frac{\mu B_{0}}{\hbar } = \left[\frac{J}{Js}\right] = \left[\frac{1}{s}\right] [/math]
Oznaczmy dalej wielkość [math]\frac{\mu B_{0}}{\hbar }[/math], w następujący sposób:
Ostatecznie, otrzymane rozwiązanie możemy przedstawić w dwóch formach:
lub
gdzie:
- [math]E = \mu B_{0}[/math]
Jak można zauważyć, rozwiązaniem równania falowego (%i 114) jest funkcja:
-
-
- ortogonalna -
-
ortonormalna, o ile zostanie spełniony warunek:
- [math] \left|a\right|^{2} + \left|b\right|^{2} = 1 [/math]
Rozwiązanie to spełnia zatem postulaty mechaniki kwantowej dotyczące postaci funkcji falowej. Wartości [math]\left|a\right|^{2}[/math] i [math]\left|b\right|^{2}[/math] można traktować jako prawdopodobieństwa znalezienia jądra atomowego w stanie odpowiednio o spinie skierowanym w górę i spinie skierowanym w dół.
Wyznaczymy teraz wartości oczekiwane operatora składowych spinu korzystając ze wzoru (%i 144). Na początku uprościmy zapis funkcji falowej. Wprowadźmy skrócone oznaczenie:
- [math] \begin{array}{l} \alpha = ae^{i\omega ^{\prime }_{0}t}\\ \beta = be^{-i\omega ^{\prime }_{0}t} \end{array} [/math]
umożliwiające zapis funkcji falowej w następującej formie
Składowa [math]z[/math] operatora spinu
- [math] \hat{C}\phi =\frac{\hbar }{2} \left[ \begin{array}{cc} 1 & 0\\ 0 & -1 \end{array} \right] \left[ \begin{array}{c} \alpha \\ \beta \end{array} \right] = \frac{\hbar }{2}\left[ \begin{array}{c} \alpha \\ -\beta \end{array} \right] [/math]
- [math] \phi ^{*}\hat{C}\phi = \frac{\hbar }{2} \left[ \begin{array}{cc} \alpha ^{*} & \beta ^{*} \end{array} \right] \left[ \begin{array}{c} \alpha \\ -\beta \end{array} \right] = \frac{\hbar }{2}\left( \begin{array}{cc} \left|\alpha \right|^{2} - \left|\beta \right|^{2} \end{array} \right) [/math]
ostatecznie:
Składowa [math]x[/math] operatora spinu
- [math] \hat{C}\phi =\frac{\hbar }{2} \left[ \begin{array}{cc} 0 & 1\\ 1 & 0 \end{array} \right] \left[ \begin{array}{c} \alpha \\ \beta \end{array} \right] = \frac{\hbar }{2}\left[ \begin{array}{c} \beta \\ \alpha \end{array} \right] [/math]
- [math] \phi ^{*}\hat{C}\phi = \frac{\hbar }{2} \left[ \begin{array}{cc} \alpha ^{*} & \beta ^{*} \end{array} \right] \left[ \begin{array}{c} \beta \\ \alpha \end{array} \right] = \frac{\hbar }{2}\left( \begin{array}{cc} \alpha ^{*}\beta - \beta \alpha ^{*} \end{array} \right) [/math]
po podstawieniu za [math]\alpha [/math] i [math]\beta [/math] odpowiednich wyrażeń otrzymujemy:
Składowa [math]y[/math] operatora spinu
- [math] \hat{C}\phi =\frac{\hbar }{2} \left[ \begin{array}{cc} 0 & -i\\ i & 0 \end{array} \right] \left[ \begin{array}{c} \alpha \\ \beta \end{array} \right] = i\frac{\hbar }{2}\left[ \begin{array}{c} -\beta \\ \alpha \end{array} \right] [/math]
- [math] \phi ^{*}\hat{C}\phi = i\frac{\hbar }{2} \left[ \begin{array}{cc} \alpha ^{*} & \beta ^{*} \end{array} \right] \left[ \begin{array}{c} -\beta \\ \alpha \end{array} \right] = \frac{\hbar }{2}\left( \begin{array}{cc} -\alpha ^{*}\beta + \beta \alpha ^{*} \end{array} \right) [/math]
po podstawieniu za [math]\alpha [/math] i [math]\beta [/math] odpowiednich wyrażeń otrzymujemy:
Podsumowując, otrzymaliśmy następujący układ równań na wartości oczekiwane składowych operatora spinu:
Z powyższych równań możemy wyciągnąć następujące, ważne wnioski:
- Jeżeli [math]\left|a\right|^{2}=1[/math] i [math]\left|b\right|^{2}=0[/math] lub gdy [math]\left|a\right|^{2}=0[/math] i [math]\left|b\right|^{2}=1[/math], czyli gdy spin jest zawsze ustawiony w górę lub w dół, to wtedy wartość oczekiwana składowej [math]z[/math] operatora spinu wynosi [math]\frac{\hbar }{2}[/math], natomiast znikają wartości oczekiwane składowych w płaszczyźnie [math]x-y[/math].
- Jeżeli [math]\left|a\right|^{2}=\left|b\right|^{2}[/math], czyli gdy tak samo prawdopodobne jest ułożenie spinu równoległe jak i antyrównoległe do osi [math]z[/math], to wtedy znika wartość oczekiwana składowej [math]z[/math] operatora spinu, natomiast wartości oczekiwane w płaszczyźnie [math]x-y[/math] są równe [math]\frac{\hbar }{2}[/math].
-
Wartość oczekiwana operatora spinu wzdłuż osi [math]z[/math] jest stała w czasie, natomiast wartości oczekiwane w płaszczyźnie [math]x-y[/math] wirują z częstością [math]2\omega ^{\prime }_{0}[/math]. Częstość [math]\omega _{0}=2\omega ^{\prime }_{0}[/math] jest nazywana częstością precesji Larmour. W przypadku protonu lub neutronu częstość Larmour można zapisać również w postaci:
- [math] \omega _{0}=2\omega ^{\prime }_{0} = 2\frac{\mu B_{0}}{\hbar } = 2\gamma B_{0}I = \gamma B_{0} [/math]
[math] \omega _{0} = \gamma B_{0} [/math]
- Wartości oczekiwane operatora spinu: [math]\left\lt \hat{s}_{x}\right\gt [/math], [math]\left\lt \hat{s}_{y}\right\gt [/math] i [math]\left\lt \hat{s}_{z}\right\gt [/math] możemy interpretować jako precesję spinu. Możemy również utworzyć wektor: [math]\left\lt \hat{s}\right\gt = \left[\left\lt \hat{s}_{x}\right\gt , \left\lt \hat{s}_{y}\right\gt , \left\lt \hat{s}_{z}\right\gt \right][/math]
-
Precesja spinu następuje zgodnie z ruchem wskazówek zegara, a więc wektor prędkości kątowej jest skierowany antyrównolegle do osi [math]z[/math]. W przypadku, kiedy cząstka lub jądro charakteryzuje się ujemnym momentem magnetycznym, precesja następuje w kierunku przeciwnym do wskazówek ruchu zegara[11]
- [math] \begin{array}{l} \hat{s}_{z} = \frac{\hbar }{2}\left(a^{2} - b^{2}\right)\\ \\ \hat{s}_{x} = \hbar ab\cos \left(2\omega _{0}t\right)\\ \\ \hat{s}_{y} = \hbar ab\sin \left(2\omega _{0}t\right) \end{array} [/math]
Rezonans magnetyczny, ujęcie kwantowe
Pod wpływem zewnętrznego pola magnetycznego [math]\vec{B}_{0}[/math] spiny jądrowe zostają uporządkowane, w wyniku czego w badanej próbce powstaje makroskopowy moment magnetyczny (namagnesowanie). Niestety, obserwowalna może być tylko składowa namagnesowania równoległa do pola [math]\vec{B}_{0}[/math].Stosowane w diagnostyce MRI pola [math]\vec{B}_{0}[/math] mają wartości od [math]0.5[/math] do [math]4[/math]T. Wytworzone przez takie pole namagnesowanie jest niewielkie i szybko zanika wraz z odległością. Zarejestrowanie na tle silnego pola [math]\vec{B}_{0}[/math] miliony razy słabszego namagnesowanie jest niezwykle trudne. Wiemy jednak, zgodnie z prawem Faradaya, że statyczne pole magnetyczne nie indukuje pola elektrycznego. Aby wyindukować pole elektryczne, potrzebna jest zmiana strumienia pola magnetycznego. Gdybyśmy potrafili w jakiś sposób wpłynąć na kierunek wytworzonego w próbce namagnesowania lub jego wielkości, moglibyśmy mierzyć sygnał elektryczny z nim związany np. przy pomocy cewek, podczas gdy pole [math]\vec{B}_{0}[/math] przez taką cewkę nie byłoby rejestrowane.
W rozdziale o zmianie orientacji wektora namagnesowania podaliśmy wzór, z których wynikało, iż obsadzenie stanów związanych ze spinem jądra atomowego wpływa na składowe wektora wartości oczekiwanej momentu magnetycznego. Powstaje zatem pytanie, w jaki sposób zaburzyć powstałą pod wpływem pola [math]\vec{B}_{0}[/math] równowagę. Jak przenieść cześć jąder z podstawowego poziomu energetycznego, do stanu wzbudzonego? Odpowiedz w ramach teorii pół-klasycznej, została podana w rozdziale [5]. Przypominamy, że próbkę trzeba umieścić w dodatkowym, słabym, zmiennym w czasie polu magnetycznym, mającym niezerowe składowe tylko w płaszczyźnie [math]x-y[/math], które oznaczymy jako [math]\vec{B}_{1}\left(t\right)[/math]. Sprawdzimy jednak, jakie są konsekwencje umieszczenia próbki w takim polu. Całkowite pole magnetyczne, w którym znajduje się badana próbka wynosi:
gdzie:
-
- [math]\vec{B}_{0} = \left[0,0, B_{0}\right][/math]
- [math]\vec{B}_{1}\left(t\right) = \left[B_{1}\cos \left(\omega t\right),-B_{1}\sin \left(\omega t\right),0\right][/math]
- [math]\vec{B}_{0} = \left[0,0, B_{0}\right][/math]
Podstawiając wzór (%i 127) do wzoru (%i 112), oraz przyjmując zgodnie ze wzorem (%i 101), że poszukujemy rozwiązania postaci:
otrzymujemy następujący układ równań:
Domyślamy się, że rozwiązaniem powyższego układu równań będą funkcje:
Wstawienie równań (%i 130) do (%i 129) daje jednorodne równanie macierzowe:
które ma nietrywialnie rozwiązanie tylko wtedy, gdy znika wyznacznik macierzy [math]\Delta [/math]. Warunek ten prowadzi do równania:
Dozwolone wartości parametru [math]\omega _{r}[/math] są zatem równe:
gdzie:
Parametr [math]\Omega [/math] nazywany jest częstością Rabiego. Rozwiązanie ogólne np. dla [math]\chi _{2}\left(t\right)[/math] będzie kombinacją liniową dwóch składowych, odpowiadającym dwóm częstościom (%i 134):
Przyjmijmy teraz, że w chwili czasu [math]t=0[/math] proton znajduje się w stanie podstawowym (czyli ma spin skierowany równolegle do pola [math]B_{0}[/math]),
wówczas:
Podstawiając (%i 135) do drugiego z równań (%i 129) daje następującą postać funkcji [math]\chi _{2}\left(t\right)[/math]:
Rozwiązanie [math]\chi _{1}\left(t\right)[/math], odpowiadające szczególnej postaci [math]\chi _{2}\left(t\right)[/math] można otrzymać korzystając z drugiego z równań (%i 129):
Podsumowując, otrzymaliśmy następujące rozwiązanie opisujące ewolucję spinu protonu w polu magnetycznym [math]\vec{B}\left(t\right)[/math]:
Obliczymy teraz prawdopodobieństwo znalezienia protonu w stanie o rzucie
spinu [math]-\frac{1}{2}[/math] w chwili czasu [math]t[/math]:
Prawdopodobieństwo to oscyluje w czasie. Oczywiście prawdopodobieństwo znalezienia protonu w stanie o rzucie spinu [math]-\frac{1}{2}[/math] jest równe [math]P_{+}\left(t\right) = 1 - P_{+}\left(t\right)[/math]. Przeanalizujmy otrzymany wynik. Amplituda oscylacji prawdopodobieństwa zależy od częstości Rabiego:
- [math] \Omega = \left[\left(\frac{\omega }{2} - \frac{\mu B_{0}}{\hbar }\right)^{2} + \left(\frac{\mu B_{1}}{\hbar }\right)^{2}\right]^{\frac{1}{2}} [/math]
Jeżeli częstość [math]\omega [/math] zmiennego pola magnetycznego będzie dowolnie duża lub dowolnie mała, częstość Rabiego osiągnie znaczne wartości, a w związku z tym prawdopodobieństwo przejścia jądra ze stanu o rzucie spinu w górę do stanu o rzucie spinu w dół będzie zawsze niskie. W momencie, gdy zostanie spełniony warunek:
przy jednoczesnym założeniu, że [math]B_{1}\ll B_{0}[/math], częstość Rabiego wyniesie:
- [math] \Omega = \left(\frac{\mu B_{1}}{\hbar }\right) [/math]
a amplituda oscylacji prawdopodobieństwa osiąga maksymalną wartość:
Równanie (%i 142) określa tzw. warunek wystąpienia zjawiska jądrowego rezonansu magnetycznego. Warto zauważyć, że energia pola magnetycznego, jaką trzeba dostarczyć, aby uzyskać przejście jądra ze stanu o rzucie spinu [math]\frac{1}{2}[/math] do stanu o rzucie spinu [math]-\frac{1}{2}[/math] jest równa różnicy energii poziomów energetycznych protonów umieszczonych w zewnętrznym polu [math]B_{0}[/math], bowiem:
Jak wiemy, częstość precesji Larmour jest równa [math]\frac{2\mu B_{0}}{\hbar}[/math], a zatem warunek rezonansowy możemy zapisać również w postaci:
Prawdopodobieństwo przejścia jądra protonu ze stanu o rzucie spinu [math]\frac{1}{2}[/math] do stanu o rzucie [math]-\frac{1}{2}[/math], równe [math]50\%[/math] zostanie osiągnięte po czasie:
czyli:
skąd dostajemy:
Jest to tzw. impuls [math]\pi [/math] — zastosowanie zmiennego pola magnetycznego o takim czasie trwania impulsu doprowadzi do zaniku namagnesowania podłużnego, powstanie natomiast namagnesowanie poprzeczne, co dokładniej omówimy w dalszej części rozdziału.
Z kolei przejścia protonu do stanu o wyższej energii nastąpi po czasie:
Jest to tzw. impuls [math]\frac{\pi }{2}[/math], powodujący zmianę orientacji spinu protonu w zewnętrznym polu magnetycznym.
Znaleźliśmy zatem sposób na zmianę orientacji spinu, a w związku z tym i namagnesowania. W warunkach rezonansu funkcja falowa spinu wyraża się następującym wzorem:
Korzystając ze wzoru na funkcję falową, podobnie jak w to uczyniliśmy w rozdziale [6], możemy policzyć składowe wektora wartości oczekiwanych operatora spinu. Wynoszą one:
Z równań tych wynika, że w płaszczyźnie [math]x-y[/math] wartość oczekiwana spinu jest superpozycją dwóch rodzajów ruchów — szybkiego, z częstością [math]2\omega _{0}[/math] (częstością Larmour) oraz modulacji [math]2\Omega _{0}[/math], natomiast składowa [math]z[/math] wartości oczekiwanej momentu magnetycznego odchyla się od kierunku zgodnego z polem [math]B_{0}[/math] (równoległego do osi [math]z[/math]) w stronę kierunku przeciwnego do kierunku do pola [math]B_{0}[/math].
Ważne uwagi
- Zarówno w rozdziale [7], gdzie opisywaliśmy precesję spinu w zewnętrznym polu magnetycznym, jak i w rozdziale bieżącym, pominęliśmy w rozwiązaniach czynnik fazowy. Pełni on jednak bardzo istotną role w opisie zjawiska NMR. W wyniku wykonywania precesji w różnej fazie przez spiny jądrowe, zanika składowa poprzeczna namagnesowania.
- W przypadku wystąpienia rezonansu jądrowego, zewnętrzne pole [math]\vec{B}_{1}\left(t\right)[/math] oprócz indukowania przejść między poziomami energetycznymi, powoduje również synchronizację składowych wartości oczekiwanych spinu w płaszczyźnie [math]x-y[/math]. Pół-klasycznym wytłumaczeniem tego efektu zajmiemy się jeszcze w następnym rozdziale. Warto jednak już w tym miejscu zapamiętać, iż procesy prowadzące do synchronizacji lub desynchronizacji ruchu spinów zawierają niezwykle cenną informację diagnostyczną.
Podsumowując:
- W zewnętrznym, statycznym polu magnetycznym, skierowanym wzdłuż osi [math]z[/math], spin protonu wykonuje ruch precesyjny z częstością Larmour. Składowa [math]z[/math] wartości oczekiwanej spinu jest stała w czasie, składowe poprzeczne wykonują ruch wirowy w płaszczyźnie [math]x-y[/math].
- Różnym ułożeniom spinu względem pola magnetycznego odpowiadają różne energie potencjalne. W przypadku spinu równego [math]\frac{1}{2}[/math] istnieją dwa poziomy energetyczne, które będą obsadzane przez jądra zgodnie z rozkładem Boltzmanna. Poziom odpowiadający równoległemu rzutowi spinu na kierunek zewnętrznego pola magnetycznego, jest korzystniejszy energetycznie, dlatego będzie obsadzany częściej.
- Desynchronizacja ruchu wirowego wartości oczekiwanej spinów w płaszczyźnie [math]x-y[/math] uniemożliwia powstanie namagnesowania poprzecznego. Obserwujemy tylko namagnesowanie podłużne.
- Pod wpływem odpowiednio dobranego pola magnetycznego, można doprowadzić do przejść między poziomami energetycznymi protonu. Jeżeli energia kwantu promieniowania jest równa różnicy poziomów energetycznych, proton absorbuje energię pola i przechodzi ze stanu o podstawowego do stanu wzbudzonego. Następnie, po pewnym czasie pozbywa się nagromadzonej energii, przechodząc z powrotem w stan podstawowy. Przejścia te możliwe są tylko wtedy, kiedy kwant promieniowania ma energię odpowiadającą częstości precesji Larmour spinu protonu w zewnętrznym polu magnetycznym [math]B_{0}[/math].
- Po pobudzeniu protonu impulsem [math]\frac{\pi }{2}[/math] zanika równowaga termodynamiczna w obsadzeniu stanów, a wraz z nią składowa [math]z[/math] wartości oczekiwanej spinu i związane nią namagnesowanie podłużne.
- Jednocześnie, w wyniku synchronizacji w płaszczyźnie [math]x-y[/math] wartości oczekiwanej spinów tych jąder atomowych, które uległy przejściu rezonansowemu, zaczyna powstawać namagnesowanie poprzeczne.
- W trakcie przechodzenia protonów ze stanu podstawowego do stanu wzbudzonego, obserwowane namagnesowanie podłużne zanika, podczas gdy narasta namagnesowanie poprzeczne. Obserwujemy zatem efekt, odchylania się wypadkowego namagnesowania od osi [math]z[/math] w kierunku płaszczyzny [math]x-y[/math].
- W wyniku procesów prowadzących do rozpraszania nagromadzonej przez proton energii oraz desynchronizacji ruchów precesyjnych zanika namagnesowanie poprzeczne, natomiast odbudowuje się składowa podłużna namagnesowania.
- Zmianom kierunku i wielkości namagnesowania towarzyszy zmiana indukcji pola elektrycznego, która może być rejestrowana przez cewki. W szczególności, sygnał pochodzący od składowej poprzecznej namagnesowania nosi nazwę sygnału FID (Free Induction Decay).
Terminy stosowane w diagnostyce MRI
- Sekwencją nazywamy w badaniu MRI serię odpowiednio impulsów, zastosowaną w celu rejestracji danych pomiarowych i odtworzenia obrazu.
- RF — Radio Frequency to impuls generujący zmienne w czasie pole magnetyczne [math]\vec{B}_{1}[/math], pod wpływem którego jądra zajmują wyższe poziomy energetyczne związane ze spinem
- TR — Repetition Time jest to czas pomiędzy kolejnymi impulsami wzbudzającymi [math]\pi/2[/math] (RF)
- TE — Echo Time jest to czas pomiędzy momentem wystąpienia impulsu pobudzającego [math]\pi/2[/math] a momentem rejestracji sygnału echa spinowego.
- FA — Flip Angle to kąt o który ma być przekręcona magnetyzacja od osi [math]z[/math] w kierunku płaszczyzny [math]x-y[/math]. Zazwyczaj jest to kąt równy 90[math]^{o}[/math], jednakże w celu przyspieszenia badania, w niektórych sekwencjach stosuje się mniejsze kąty.
- TI — Inversion Time jest to czas pomiędzy impulsem pobudzającym [math]\pi[/math] (zmiana orientacji spinu o 180[math]^{o}[/math]) a impulsem pobudzającym [math]\pi/2[/math].
- NA or NEX Number of Acquisitions to liczba powtórzeń pomiaru. W celu uzyskania wysokiego SNR, pomiary można powtarzać wielokrotnie. Redukcja szumu maleje proporcjonalne do [math]\sqrt{\textrm{NA}}[/math].
- ↑ W języku angielskim słowo spin oznacza wirowanie
- ↑ 2,0 2,1 2,2 2,3 2,4 2,5 2,6 H.Haken H.Ch.Wolf "Atomy i kwanty"
- ↑ P. C. Lauterbur. Image formation by induced local interactions: examples employing nuclear magnetic resonance. Nature 242, 190-191 (1973)
- ↑ P. Mansfield, P.K. Grannell, J. Phys. C: Solid State Phys. 6, L422 (1973)
- ↑ Należy również pamiętać, iż wyznaczona gęstość jąder atomowych (w praktyce jąder atomu wodoru) zależy również od czasu powtarzania wzbudzeń jąder atomowych (Time Repetition —TR) oraz czasu echa spinowego (Time Echo — TE)
- ↑ 6,0 6,1 6,2 6,3 6,4 6,5 Iwo Białynicki-Birula, Marek Cieplak, Jerzy Kamiński Teoria Kwantów. Mechanika Falowa. Wydawnictwo Naukowe PWN, Warszawa 1991.
- ↑ Warunek unormowania został arbitralnie wprowadzony w pierwszej pracy Schrödingera dotyczącej równania falowego.
- ↑ Richard L. Liboff Wstęp do Mechaniki Kwantowej. Państwowe Wydawnictwo Naukowe, Warszawa 1987.
- ↑ Leszek Adamowicz Mechanika Kwantowa. Formalizm i Zastosowania. Oficyna Wydawnicza Politechniki Warszawskiej, Warszawa 2005.
- ↑ W języku angielskim słowo spin oznacza wirowanie
- ↑ [math]\cos \left(-2\omega _{0}\right)=\cos \left(2\omega _{0}\right)[/math], zaś [math]\sin \left(-2\omega _{0}\right)=-\sin \left(2\omega _{0}\right)[/math]