Ćwiczenia 1

Narzędzia wykorzystywane na ćwiczeniach

Python

Python jest językiem programowania wysokiego poziomu, który w połączeniu z bibliotekami NumPy i SciPy do obliczeń naukowych pozwala na szybkie i wygodne programowanie lub analizowanie danych w sposób interaktywny. Przykłady prezentowane w ramach zajęć powinny uruchamiać się zarówno w wersji 2 jak i 3 języka Python, jednak zachęcamy Państwa, aby od początku uczyć się i korzystać z wersji 3 języka.

Dokumentacja modułu scipy.signal

Proszę zapoznać się z dokumentacją biblioteki scipy.signal:

http://docs.scipy.org/doc/scipy-0.14.0/reference/signal.html

Svarog

Przydatnym narzędziem do analizy sygnałów, z którego będziemy korzystać na zajęciach, jest program SVAROG (pierwotnie skrót od Signal Viewer, Analyzer and Recorder On GPL). Program działa w środowisku Java, jest więc niezależny od systemu operacyjnego (Linux, Windows, OS X…). Svarog pozwala na wczytywanie i analizowanie sygnałów (nie tylko bioelektrycznych), zarówno przy użyciu prostych (FFT, spektrogram) jak i bardziej zaawansowanych (matching pursuit, ICA, DFT itd.) narzędzi. Dzięki współpracy z platformą OpenBCI, możliwa jest rejestracja sygnału (łącznie z metadanymi) bezpośrednio z poziomu graficznego interfejsu użytkownika.

Svarog: uruchamianie i konfiguracja

Aktualną wersję programu Svarog można pobrać stąd. Program nie wymaga instalacji. Po rozpakowaniu paczki do dowolnego katalogu należy uruchomić skrypt „run-svarog.sh” lub uruchomić bezpośrednio plik *.jar.

W przypadku pracy na własnych komputerach, do prawidłowego uruchomienia pluginu do analizy sygnałów, z którego będziemy korzystać w dalszej części ćwiczeń, konieczne jest zainstalowanie środowiska Oracle Java SE w wersji 8, które można pobrać ze strony wydawcy. Alternatywnie, użytkownicy systemu Ubuntu lub pokrewnych dystrybucji mogą zainstalować środowisko Java według instrukcji dostępnych na tej stronie.

Sygnały ciągłe i dyskretne

Próbkowanie w czasie

Proszę powtórzyć sobie pojęcia:

• częstość próbkowania
• częstość Nyquista
• aliasing

W poniższym ćwiczeniu chcemy zbadać efekt próbkowania sygnału w czasie. W komputerach nie mamy dostępu do sygnału ciągłego. Na nasze potrzeby wygenerujemy sygnały próbkowane z bardzo dużą częstością, które będą dla nas aproksymacją sygnałów ciągłych. Przy ich pomocy zaprezentujemy efekt utożsamiania (aliasingu).

Proszę wytworzyć wektor reprezentujący czas „prawie” ciągły. Będzie to u nas 1000 wartości z przedziału [0,1) wziętych z odstępem 0,001.

# -*- coding: utf-8 -*-

import pylab as py
import numpy as np

t = np.arange(0,1,0.001) # czas 'prawie ciągły'

Teraz proszę wygenerować dwie sinusoidy: jedną o częstości -1 a drugą o częstości 9. Dla przypomnienia wyrażenie:

[math] s(t) = \sin(2 \pi f t)[/math] możemy w pythonie zapisać:

s = np.sin(2*np.pi*f*t)

Proszę wykreślić obie sinusoidy.

Teraz proszę spróbkować czas i nasze „prawie” ciągłe sinusoidy z okresem próbkowania 0,1. (Trzeba pobrać co 100 element, proszę posłużyć się wycinkami) Na tle „prawie” ciągłych sinusoid proszę dorysować punkty ze spróbkowanych sygnałów. Aby punkty były dobrze widoczne proponuję użyć markerów x oraz +.

Proszę zaobserwować wzajemne położenie punktów. Czy można odróżnić sinusoidę o częstości −1 od sinusoidy o częstości 9, jeśli obie są próbkowane z częstością 10? Jak można uogólnić tą obserwację?

 *

Sygnały testowe

Generowanie sygnałów testowych

Do badania różnych metod analizy sygnałów potrzebne nam będą sygnały o znanych własnościach. W szczególności dobrze jest umnieć nadać sygnałom występującym w postaci cyfrowej, oraz sztucznym sygnałom próbnym pewne własności fizyczne takie jak:

• czętość próbkowania
• czas trwania
• amplituda

Przykład sinus

Sinus o zadanej częstości (w Hz), długości trwania, częstości próbkowania i fazie. Poniższy kod implementuje i testuje funkcję

[math] \sin(f,T,Fs,\phi) = \sin(2*\pi f t)[/math] dla [math]t \in \{0,T\}[/math]

# -*- coding: utf-8 -*-

import pylab as py
import numpy as np

def sin(f = 1, T = 1, Fs = 128, phi =0 ):
	'''sin o zadanej częstości (w Hz), długości, fazie i częstości próbkowania
	Domyślnie wytwarzany jest sygnał reprezentujący 
	1 sekundę sinusa o częstości 1 Hz i zerowej fazie próbkowanego 128 Hz
	'''

	dt = 1.0/Fs
	t = np.arange(0,T,dt)
	s = np.sin(2*np.pi*f*t + phi)
	return (s,t)
	
	
(s,t) = sin(f=10,Fs=1000)
py.plot(t,s)
py.show()

Przykład: eksport sygnału do pliku binarnego

• Poniższy kod ilustruje sposób zapisu dwóch funkcji sinus o częstościach 10 Hz i 21 Hz do pliku binarnego:

# -*- coding: utf-8 -*-

import numpy as np

T = 5
Fs = 128.0

s1 = sin(f=10, T=T, Fs=Fs)
s2 = sin(f=21, T=T, Fs=Fs)	
	
signal = np.zeros((T*Fs, 2), dtype='<f')
signal[:, 0] = s1
signal[:, 1] = s2

with open('test_signal.bin', 'wb') as f:
    signal.tofile(f)

Przykład: wczytanie sygnału do Svaroga

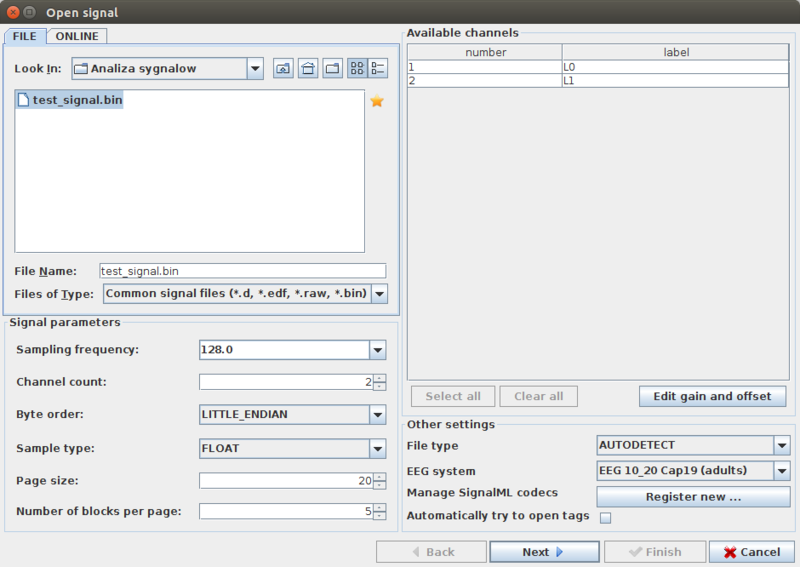
W celu wczytania zapisanego binarnie sygnału do programu Svarog, po wybraniu File -> Open signal, należy wprowadzić częstość próbkowania sygnału oraz liczbę kanałów.

Wczytywanie sygnału w programie Svarog.

Delta

Podobnie można zdefiniować funkcję delta o zadanym czasie trwania, częstości próbkowania i momencie wystąpienia impulsu:

[math] \delta(t_0) = \left\{^{1 \quad t=t_0} _{0 \quad t \ne t_0} \right.[/math]

def delta(t0=0.5, T=1  ,Fs = 128):
	dt = 1.0/Fs
	t = np.arange(0,T,dt)
	d = np.zeros(len(t))
	d[np.ceil(t0*Fs)]=1
	return (d,t)

Zadanie:

Analogicznie do powyższych przykładów proszę zaimplementować i przetestować funkcje generujące:

• funkcję Gabora (funkcja Gaussa modulowana cosinusem) o zadanej częstości i standardowym odchyleniu w czasie, momencie wystąpienia, długości, częstości próbkowania i fazie.

[math] g = \exp\left(-\frac{1}{2}\left(\frac{t-t_0}{\sigma}\right)^2 \right) \cdot \cos(2 \pi f t + \phi); [/math]

• szum gaussowski o zadanej średniej, odchyleniu standardowym, długości i częstości próbkowania.