STATLAB/Zadanie zaliczeniowe3: Różnice pomiędzy wersjami
Z Brain-wiki
| Linia 7: | Linia 7: | ||
===2. Analiza czasowa widma=== | ===2. Analiza czasowa widma=== | ||
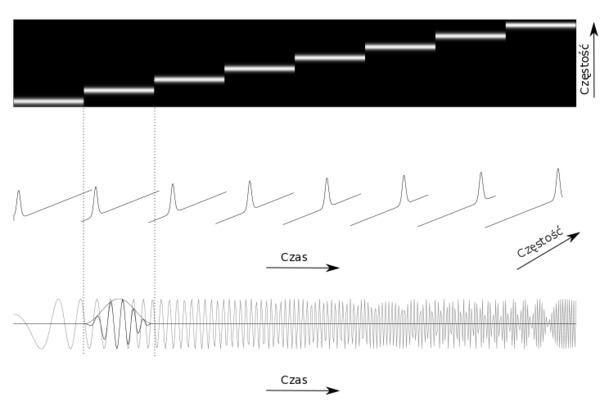
| − | + | Programistyczna część projektu polega na samodzielnej implementacji spektrogramu. Spektrogram otrzymujemy w następujący sposób: | |
| − | + | * sygnał dzielimy na fragmenty o długości '''N_okna''' | |
| − | + | * fragmenty mogą ale nie muszą na siebie nachodzić. Liczba próbek nachodzących niech będzie oznaczona '''N_wsp''' | |
| − | + | * dla każdego fragmentu estymujemy widmo gęstości energii za pomocą periodogramu z okienkiem '''okno''' | |
| − | + | * widma kolejnych fragmentów zapisujemy w macierzy numpy, tak, że i-ta kolumna zawiera widmo i-tego fragmentu | |
| − | + | [[Plik:spectrogram.png|600px|thumb|left|Idea tworzenia spektrogramu]] | |
| − | |||
| − | że | ||
| − | |||
| − | |||
===3. Prezentacja=== | ===3. Prezentacja=== | ||
Wersja z 09:45, 19 lis 2016
1. Dane
Poniżej znajdyją się linki do dwóch fragmentów utworów audio. Zapisane są w formacie wav. Pliki takie można wczytać do programu pythonowego za pomocą funkcji scipy.io.wavfile.read( dokumentacja tej funkcji.)
Candy_Dulfer_-_Lily_Was_Here.wav
Rupert_Blaise_-_06_-_What_A_Wonderful_World.wav
2. Analiza czasowa widma
Programistyczna część projektu polega na samodzielnej implementacji spektrogramu. Spektrogram otrzymujemy w następujący sposób:
- sygnał dzielimy na fragmenty o długości N_okna
- fragmenty mogą ale nie muszą na siebie nachodzić. Liczba próbek nachodzących niech będzie oznaczona N_wsp
- dla każdego fragmentu estymujemy widmo gęstości energii za pomocą periodogramu z okienkiem okno
- widma kolejnych fragmentów zapisujemy w macierzy numpy, tak, że i-ta kolumna zawiera widmo i-tego fragmentu
3. Prezentacja
Macierz wykreśl przy pomocy funkcji pylab.imshow, podając zakresy poszczególnych osi przy użyciu parametru
[math] \textrm{extent} = (t_{min}, t_{max}, f_{min}, f_{max}) \,. [/math]
4. Interpretacja wyniku
Powtórz punkty 2 i 3 dla kilku różnych szerokości okien [math]N_w[/math] i zinterpretuj widoczne różnice.