TI/Programowanie dla Fizyków Medycznych/RRZ

Równania różniczkowe zwyczajne

Zajmieny się teraz problemem numerycznego rozwiązywania równań różniczkowych zwyczajnych o postaci:

[math] \frac{dy(t)}{dt} = f(t,y(t))[/math],

z warunkeim początkowym

[math]y(t_0)=y_0[/math].

Zauważmy, że przykładowe równanie różniczkowe drugiego rzędu

[math] \frac{d^2 x(t)}{dt^2} = \omega(t,x(t))[/math],

można zapisać jako

[math] \frac{d}{dt} \binom{x(t)}{x'(t)} = \binom{x'(t)}{\omega(t,x(t))}[/math].

W analogiczny sposób równanie dowolnego rzędy możemy zapisać jako wektorowe równanie różniczkowe pierwszego rzędu. Wystarczy zatem, że skupimy się na rozwiązywaniu równań pierwszego rzędu, Rozwiązaniem postawionego problemu są ciągłe funkcje zmiennej czasowej t. Rozwiązanie numeryczne takiego problemu ogranicza się jednak do znalezienia wartości funkcji y(t) w skończonej liczbie punktów czasowych. W najprostrzym przypadku (do którego się tutaj ograniczymy) zakładamy, że punkty te są od siebie równo oddalone, a odległość między nimi nazywamy krokiem czasowym i tradycyjnie oznaczamy literą h. Zatem rozwiązanie równania na przedziale [math](t_0,t_k)[/math] sprwadzamy do rozwiązania w sekwencji czasów [math]t_0, t+1=t_0+h,t_2=t_0+2h,...,t_k=Nh[/math]. Poprzez [math]x_n[/math] oznaczać będziemy numeryczne przybliżenie ścisłego rozwiązania [math]x(t_n)[/math].

Metoda Eulera

Najprostszą metodą numeryczną rozwiązywania równań różniczkowych jest metoda Eulera. Przybliżmy pochodzną czasową występującą po lewej stronie równania przez iloraz różnicowy

[math] \frac{d x(t)}{dt} \approx \frac{x(t+h)-x(t)}{h}[/math],

przekształacjąc uzyskujemy

[math] x(t+h) \approx x(t)+ h \frac{d x(t)}{dt} [/math]

a po podstawieniu rozwiązywanego równania mamy

[math] x(t+h) \approx x(t)+ h f(t,x(t)) [/math].

Możemy to zapisać w postaci dyskretnej

[math] x_{n+1} \approx x_n + h f(t_n,x_n) [/math].

Wartość w kolejnej chwili czasu dana jest explicite poprzez wartość w chwili poprzedniej. Metoda ta nazywa się Explicit Euler. Możemy teraz zaimplementować ją w pythonie

import numpy as np
import pylab as py

#rozwiazujemy rownanie dx(t)/dt=f(t,x)

#metoda Explicit Euler
#f - funkcja f z rownania
#x0-wartosc poczatkowa
#t0-czas poczatkowy
#tk-czas koncowy
#h-krok czasowy

def EE(f,x0,t0,tk,h): 
    #generujemy wektor czasow
    t=np.arange(t0,tk,h)

    #liczba krokow czasowych
    N=len(t)

    #wektor wynikowy
    if hasattr(x0, "__len__"): x=np.zeros((N,len(x0))) # gdy mamy doczynienia w równaniem wektorowym
    else: x=np.zeros(N) #dla przypadku skalarnego

    #wpisujemy wartosc poczatkowa
    x[0]=np.array(x0)
    #index
    i=1
    #petla glowna
    while (i<N):
        x[i]=np.array(x[i-1]+h*f(t[i-1],x[i-1]))
        i+=1
    return t,x

Najłatwiej będzie przetestować napisaną metodę na równaniu którego ścisłe rozwiązanie jest znane.Zacznijmy zatem od równania oscylatora harmonicznego

def oscylator(t,y):
    x=y[0]
    xdot=y[1]
    return np.array([xdot,-x])

Rozwiążmy to równanie z warunkeim początkowym [1.0,1.0] i od czasu od 0 do 100.

t,x=EE(oscylator,[1.0,1.0],0.0,100,0.01)
py.plot(t,x[:,0])
py.show()

rozwiązanie wygląda wówczas nastepująco

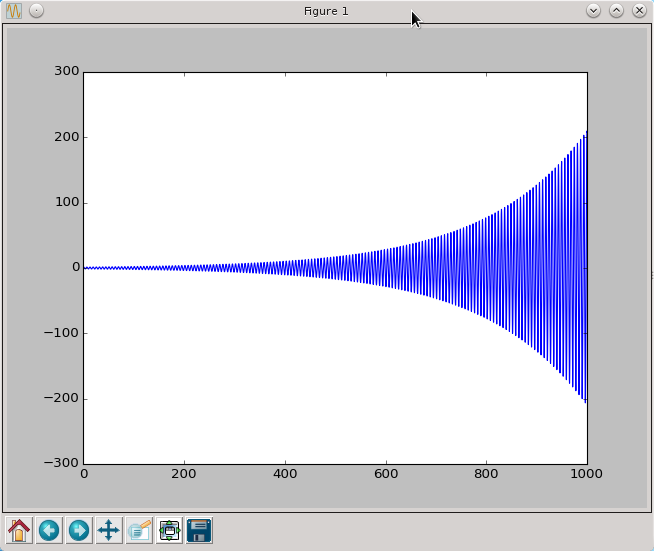
Jeżeli zaś wydłuzymy czas symulacji to 1000 otrzymamy

def leapfrog(f,x0,t0,tk,h): 
    #generujemy wektor czasow
    t=np.arange(t0,tk,h)
    #liczba krokow czasowych
    N=len(t)
    #wektor wynikowy
    if hasattr(x0, "__len__"): x=np.zeros((N,len(x0)))
    else: x=np.zeros(N)
    #wpisujemy wartosc poczatkowa
    x[0]=np.array(x0)
    #index
    i=1
    #petla glowna
    while (i<N):
        k1=f(t[i-1],x[i-1])
        k2=f(t[i-1]+h*0.5,x[i-1]+0.5*h*k1)
        x[i]=np.array(x[i-1]+h*k2)
        i+=1
    return t,x

def Heun(f,x0,t0,tk,h): 
    #generujemy wektor czasow
    t=np.arange(t0,tk,h)
    #liczba krokow czasowych
    N=len(t)
    #wektor wynikowy
    if hasattr(x0, "__len__"): x=np.zeros((N,len(x0)))
    else: x=np.zeros(N)
    #wpisujemy wartosc poczatkowa
    x[0]=np.array(x0)
    #index
    i=1
    #petla glowna
    while (i<N):
        k1=f(t[i-1],x[i-1])
        k2=f(t[i-1]+h*0.5,x[i-1]+0.5*h*k1)
        x[i]=np.array(x[i-1]+h*0.5*(k1+k2))
        i+=1
    return t,x

def RK4(f,x0,t0,tk,h): 
    #generujemy wektor czasow
    t=np.arange(t0,tk,h)
    #liczba krokow czasowych
    N=len(t)
    #wektor wynikowy
    if hasattr(x0, "__len__"): x=np.zeros((N,len(x0)))
    else: x=np.zeros(N)
    #wpisujemy wartosc poczatkowa
    x[0]=np.array(x0)
    #index
    i=1
    #petla glowna
    while (i<N):
        k1=h*f(t[i-1],x[i-1])
        k2=h*f(t[i-1]+h*0.5,x[i-1]+0.5*k1)
        k3=h*f(t[i-1]+h*0.5,x[i-1]+0.5*k2)
        k4=h*f(t[i-1]+h,x[i-1]+k3)
        x[i]=np.array(x[i-1]+(k1+2.0*k2+2.0*k3+k4)/6)
        i+=1
    return t,x

#Metoda Verlet sluzy do rozw. rownan rowniczkowych typu:
# d^2 x(t)/dt^2=a(x(t))
# x_(n+1)=x_n+v_n*h+1/2 a(x_n)*h^2
# v_n=(x_n-x_(n-1))/h
#podstawiamy do poprzedniego
# x_(n+1)=2*x_n-x_(n-1)+1/2 a(x_n)*h^2
#przekształcają otrzymamy
# x_(n-1)=2*x_n-x_(n+1)+1/2 a(x_n)*h^2
#zatem algorytm jest symetryczny w czasie
#rownanie ma postac:
#d(x,x')/dt=(x',x'')=f(t,(x,x'))
def Verlet(f,x0,t0,tk,h): 
    #generujemy wektor czasow
    t=np.arange(t0,tk,h)
    #liczba krokow czasowych
    N=len(t)
    if len(x0)!=2:
        print 'algorytm dziala tylko dla rown. 2 rzedu'
        return None
    x=np.zeros((N,2))
    #wpisujemy wartosc poczatkowa
    x[0]=np.array(x0)
    x[1]=np.array(x0)
    #index
    i=2
    #petla glowna
    while (i<N):
        x_i=2*x[i-1][0]-x[i-2][0]+0.5*h*h*f(t[i-1],x[i-1])[1]
        v_i=(x_i-x[i-1][0])/h
        x[i]=np.array([x_i,v_i])
        i+=1
    return t,x

#tłumienie
#t,x=EE(lambda x:-x,1.0,0.0,100.0,0.01)
#py.plot(t,x)
#py.show()



#t,x=EE(oscylator,[1.0,1.0],0.0,1000.0,0.01)
t,x=leapfrog(oscylator,[1.0,1.0],0.0,100000.0,0.1)
py.plot(x[:,0],x[:,1])
py.show()
#Ec=map(lambda z:z[0]**2+z[1]**2,x)
#py.plot(t,Ec)
py.show()

Wahadło

import numpy as np
import pylab as py

def RK4(f,x0,t0,tk,h): 
    #generujemy wektor czasow
    t=np.arange(t0,tk,h)
    #liczba krokow czasowych
    N=len(t)
    #wektor wynikowy
    if hasattr(x0, "__len__"): x=np.zeros((N,len(x0)))
    else: x=np.zeros(N)
    #wpisujemy wartosc poczatkowa
    x[0]=np.array(x0)
    #index
    i=1
    #petla glowna
    while (i<N):
        k1=h*f(t[i-1],x[i-1])
        k2=h*f(t[i-1]+h*0.5,x[i-1]+0.5*k1)
        k3=h*f(t[i-1]+h*0.5,x[i-1]+0.5*k2)
        k4=h*f(t[i-1]+h,x[i-1]+k3)
        x[i]=np.array(x[i-1]+(k1+2.0*k2+2.0*k3+k4)/6)
        i+=1
    return t,x


#oscylator harmoniczny
def oscylator(t,y):
    f0=1.0
    w0=1.0
    
    x=y[0]
    xdot=y[1]
    return np.array([xdot,f0*np.cos(oscylator.W*t)-oscylator.Gamma*xdot-w0*w0*x])

def amplituda(x):
    lista=x[2000:,0]
    return (max(lista)-min(lista))*0.5

def okres(t,x):
    t=t[2000:]
    x=x[2000:,0]
    czasyMaksimow=[]
    for i in xrange(1,len(x)-1):
        if x[i]>x[i-1] and x[i]>x[i+1]:
            czasyMaksimow.append(t[i])
    return np.mean(np.diff(czasyMaksimow))
    

oscylator.W=1.0
oscylator.Gamma=0.1

#Amplituda wahań w funkcji Omega (częstości wymuszania)
#Omegas=np.arange(0.1,3.0,0.05)
#amp=[amplituda(RK4(oscylator,[0.0,1.0],0.0,400.0,0.1)[1]) for oscylator.W in Omegas]
#py.plot(Omegas,amp)
#py.show()

#Okres wahań w funkcji Omega (częstości wymuszania)
#Omegas=np.arange(0.1,3.0,0.1)
#okresy=[okres(*RK4(oscylator,[0.0,1.0],0.0,400.0,0.1)) for oscylator.W in Omegas]
#py.plot(Omegas,okresy)
#py.show()

#Amplituda wahań w funkcji wsp. tłumienia Gamma
Gammas=np.arange(0.1,3.0,0.1)
amp=[amplituda(RK4(oscylator,[0.0,1.0],0.0,400.0,0.1)[1]) for oscylator.Gamma in Gammas]
py.plot(Gammas,amp)
py.show()

Zadanie

Rozwiąż układ równań różniczkowych Lorenza dany wzorami

[math] \begin{cases}\dot x=\sigma y-\sigma x\\\dot y=-xz+rx-y\\\dot z=xy-bz\end{cases}, [/math]

metodą całkowania Rungego–Kutty drugiego rzędu z α = 2/3, czyli

[math] k_1 &= f(t_n,y_n), \\k_2 &= f(t_n + \tfrac{2}{3}h, y_n + \tfrac{2}{3}h k_1), \\y_{n+1} &= y_n + h\left(\tfrac{1}{4}k_1+\tfrac{3}{4}k_2\right). [/math]

Przyjmij sigma=10, b=8/3, r=99.96, krok czasowy h=0.005 i warunki początkowe x=1,y=0,z=0. Wykonaj 8000 kroków czasowych. Układ po pewnym czasie zacznie poruszać się po pewnej periodycznej trajektorii. Wykonaj 3 rysunki TEJ PERIODYCZNEJ TRAJEKTORII (bez okresu dochodzenia do niej) w płaszczyznach (x,y), (y,z) i (z,x). Wypisz na ekranie przedziały wartości jakie przyjmują zmienne x,y i z na periodycznej trajektorii oraz okres trajektorii periodycznej.

import numpy as np
import pylab as py

#rozwiazujemy rownanie dx(t)/dt=f(t,x)

#metoda Explicit Euler
#f - funkcja f z rownania
#x0-wartosc poczatkowa
#t0-czas poczatkowy
#tk-czas koncowy
#h-krok czasowy

def RK2(f,x0,t0,tk,h): 
    #generujemy wektor czasow
    t=np.arange(t0,tk,h)
    #liczba krokow czasowych
    N=len(t)
    #wektor wynikowy
    if hasattr(x0, "__len__"): x=np.zeros((N,len(x0)))
    else: x=np.zeros(N)
    #wpisujemy wartosc poczatkowa
    x[0]=np.array(x0)
    #index
    i=1
    #petla glowna
    while (i<N):
        k1=h*f(t[i-1],x[i-1])
        k2=h*f(t[i-1]+h*2.0/3.0,x[i-1]+k1*2.0/3.0)
        x[i]=np.array(x[i-1]+0.25*k1+0.75*k2)
        i+=1
    return t,x

#uklad Lorenza
def Lorenza(t,y):
    sigma=10.0
    b=8.0/3
    r=99.96
    xx=y[0]
    yy=y[1]
    zz=y[2]
    xdot=sigma*(yy-xx)
    ydot=-xx*zz+r*xx-yy
    zdot=xx*yy-b*zz
    return np.array([xdot,ydot,zdot])

t,x=RK2(Lorenza,[1.0,0.0,0.0],0.0,40.0,0.005)
py.plot(x[2500:,0],x[2500:,1])
py.show()
py.plot(x[2500:,1],x[2500:,2])
py.show()
py.plot(x[2500:,2],x[2500:,0])
py.show()

#szukanie okresu
prog=140
lista=[]
for i in range(2500,8000):
    if (x[i-1,2]<prog) and (x[i,2]>prog): lista.append(i)
print 'okres to:',np.mean(np.diff(lista)*0.005)
print 'zmienna x przyjmuje wartosci z zakresu: (',min(x[2500:,0]),',',max(x[2500:,0]),')'
print 'zmienna y przyjmuje wartosci z zakresu: (',min(x[2500:,1]),',',max(x[2500:,1]),')'
print 'zmienna z przyjmuje wartosci z zakresu: (',min(x[2500:,2]),',',max(x[2500:,2]),')'

"Programowanie dla Fizyków Medycznych"