Funkcje trygonometryczne
Spis treści
- 1 Funkcje trygonometryczne w trójkącie prostokątnym
- 2 Miara łukowa kąta
- 3 Funkcje trygonometryczne dowolnego kąta
- 3.1 Znaki funkcji trygonometrycznych w poszczególnych ćwiartkach układu współrzędnych
- 3.2 Wartości funkcji trygonometrycznych dla niektórych wartości kątów
- 3.3 Parzystość i nieparzystość funkcji trygonometrycznych
- 3.4 Okresowość funkcji trygonometrycznych
- 3.5 Związki pomiędzy funkcjami trygonometrycznymi tego samego kąta, tzn. tożsamości trygonometryczne
- 3.6 Związki pomiędzy funkcjami trygonometrycznymi różnych kątów
- 3.7 Wzory redukcyjne na sprowadzanie kąta do pierwszej ćwiartki
- 4 Funkcje odwrotne do funkcji trygonometrycznych
- 5 Biegunowy układ współrzędnych
- 6 Twierdzenie kosinusów
- 7 Twierdzenie sinusów
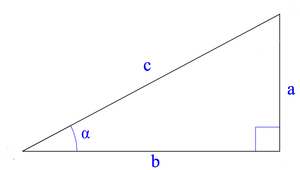
Funkcje trygonometryczne w trójkącie prostokątnym
Sinus
Sinusem kąta ostrego w trójkącie prostokątnym nazywamy stosunek przyprostokątnej przeciwległej danemu kątowi do przeciwprostokątnej:
Kosinus
Kosinusem kąta ostrego w trójkącie prostokątnym nazywamy stosunek przyprostokątnej przyległej do danego kąta do przeciwprostokątnej:
Tangens
Tangensem kąta ostrego w trójkącie prostokątnym nazywamy stosunek przyprostokątnej przeciwległej danemu kątowi do przyprostokątnej przyległej do danego kąta:
Kotangens
Kotangensem kąta ostrego w trójkącie prostokątnym nazywamy stosunek przyprostokątnej przyległej do danego kąta do przyprostokątnej przeciwległej danemu kątowi:
Uwaga
Czasem, choć rzadko, używa się też funkcji sekans i kosekans. Są one definiowane jako:
- [math]{\rm sec}\,\alpha = \frac{1}{\sin\alpha}\;[/math]
- [math]{\rm \mathop{cosec}}\,\alpha = \frac{1}{\cos\alpha}\;[/math].
Miara łukowa kąta
Def. 1 radian (1 rad) jest to miara kąta opartego na łuku, którego długość jest równa długości promienia okręgu. Mamy więc proste wzory na zamianę miary kąta w stopniach [math]\alpha_s\;[/math] na miarę łukową [math]\alpha_r\;[/math]:
W szczególności: [math]180^o=\pi \;[/math] (rad); [math]90^o=\frac{\pi}{2}\;[/math]; [math]60^o=\frac{\pi}{3}\;[/math]; [math]30^o=\frac{\pi}{6}\;[/math] (podając kąt w mierze łukowej, często się już nie podaje że jest on mierzony w radianach).
Funkcje trygonometryczne dowolnego kąta
Mając zdefiniowane funkcje trygonometryczne dla dowolnego kąta [math]\alpha\in [0, \frac{\pi}{2}[\;[/math], łatwo rozszerzyć te definicje na dowolny inny kąt. Robi się to tak:
Niech [math]\alpha\;[/math] będzie kątem skierowanym umieszczonym w ukł wsp. tak, że jego początkowe ramię pokrywa się z dodatnią półosią [math]OX\;[/math], a końcowym ramieniem jest półprosta o początku w punkcie [math](0,0)\;[/math]. Na końcowym ramieniu wybieramy dowolny punkt [math]P = (x,y)\;[/math], różny od punktu [math](0,0)\;[/math].
Funkcje trygonometryczne kąta [math]\alpha\;[/math] definiujemy w sposób następujący:
gdzie [math]r\;[/math] jest odległością punktu [math]P\;[/math] od punktu [math](0,0)\;[/math],zaś [math]r=\sqrt{x^2+y^2}\;[/math].
Znaki funkcji trygonometrycznych w poszczególnych ćwiartkach układu współrzędnych
"W pierwszej wszystkie są dodatnie, W drugiej tylko sinus, W trzeciej tangens i kotangens, A w czwartej kosinus".
Wartości funkcji trygonometrycznych dla niektórych wartości kątów
| stopnie | [math]0^\circ\;\;[/math] | [math]30^\circ\;\;[/math] | [math]45^\circ\;\;[/math] | [math]60^\circ\;\;[/math] | [math]90^\circ\;\;[/math] |
|---|---|---|---|---|---|
| [math]\sin\;\;[/math] | [math]0\;\;[/math] | [math] \tfrac{1}{2} \;[/math] | [math] \tfrac{\sqrt{2}}{2} \;[/math] | [math] \tfrac{\sqrt{3}}{2} \;[/math] | [math]1\;\;[/math] |
| [math]\cos\;\;[/math] | [math]1\;\;[/math] | [math] \tfrac{\sqrt{3}}{2} \;[/math] | [math] \tfrac{\sqrt{2}}{2} \;[/math] | [math] \tfrac{1}{2} \;[/math] | [math]0\;\;[/math] |
| [math]\tg\;\;[/math] | [math]0\;\;[/math] | [math] \tfrac{\sqrt{3}}{3} \;[/math] | [math]1\;\;[/math] | [math] \sqrt{3} \;[/math] | NI |
| [math]\ctg\;\;[/math] | NI | [math] \sqrt{3} \;[/math] | [math]1\;\;[/math] | [math] \tfrac{\sqrt{3}}{3} \;[/math] | [math]0\;\;[/math] |
| [math]\sec\;\;[/math] | [math]1\;\;[/math] | [math] \tfrac{2\sqrt{3}}{3} \;[/math] | [math] \sqrt{2} \;[/math] | [math]2\;\;[/math] | NI |
| [math]\csc\;\;[/math] | NI | [math]2\;\;[/math] | [math]\sqrt{2}\;[/math] | [math] \tfrac{2\sqrt{3}}{3} \;[/math] | [math]1\;\;[/math] |
Parzystość i nieparzystość funkcji trygonometrycznych
- Funkcja [math]f(x)=\cos(x)\;[/math] jest parzysta: [math]\cos(-x) = \cos(x)\;[/math] [math]\forall_{x\in\mathbb R}\;[/math]
- Funkcja [math]f(x)=\sin(x)\;[/math] jest nieparzysta: [math]\sin(-x) = \sin(x)\;[/math] [math]\forall_{x\in\mathbb R}\;[/math]
- Funkcja [math]f(x)=\tg(x)\;[/math] jest nieparzysta: [math]\tg(-x) = -\tg(x)\;[/math] [math]\forall_{x\in D_f}\;[/math]
- Funkcja [math]f(x)=\ctg(x)\;[/math] jest nieparzysta: [math]\ctg(-x) = \ctg(x)\;[/math] [math]\forall_{x\in D_f}\;[/math]
Okresowość funkcji trygonometrycznych
- Okresem podstawowym funkcji [math]y=\sin x\;[/math] oraz [math]y=\cos x\;[/math] jest [math]2\pi\;[/math]:
Zachodzi: [math]\sin(x+2k\pi)=\sin(x)\;[/math] oraz [math]\cos(x+2k\pi)=\cos(x)\;[/math] [math]\forall_{x\in\mathbb R}, \forall_{k\in\mathbb Z}\;[/math]. - Okresem podstawowym funkcji [math]y=\tg x\;[/math] oraz [math]y=\ctg x\;[/math] jest [math]\pi\;[/math]:
Zachodzi: [math]\tg(x+k\pi)=\tg(x)\;[/math] oraz [math]\ctg(x+k\pi)=\ctg(x)\;[/math] [math]\forall_{x\in D_f}, \forall_{k\in\mathbb Z}\;[/math].
Związki pomiędzy funkcjami trygonometrycznymi tego samego kąta, tzn. tożsamości trygonometryczne
- [math]\sin^2\alpha + \cos^2\alpha=1 \,\;[/math] [math]\forall_{\alpha\in\mathbb R}\;[/math] — jest to tzw. jedynka trygonometryczna;
- [math]\tg\alpha = \frac{\sin\alpha}{\cos\alpha},\;\; \alpha\ne \frac{\pi}{2}+ k\pi,\; k\in\mathbb Z\;[/math];
- [math]\ctg\alpha = \frac{\cos\alpha}{\sin\alpha},\;\; \alpha\ne k\pi,\; k\in\mathbb Z\;[/math];
- [math]\tg\alpha\,\ctg\alpha = 1,\;\; \alpha\ne \frac{k\pi}{2},\; k\in\mathbb Z\;[/math]
Przy użyciu tych tożsamości trygonometrycznych można udowodnić wiele innych — zależnie od potrzeby.
Związki pomiędzy funkcjami trygonometrycznymi różnych kątów
Dla dowolnych kątów [math]\alpha,\beta\;[/math] zachodzą związki:
- [math]\sin(\alpha+\beta)=\sin\alpha \, \cos\beta + \cos\alpha\, \sin\beta\;[/math]
- [math]\cos(\alpha+\beta) = \cos\alpha \, \cos\beta - \sin\alpha \, \sin\beta\;[/math]
Dow. Wynikają z nich, po przyjęciu [math]\alpha=\beta\;[/math], związki na funkcje trygonometryczne podwojonego kąta
[math]\sin 2 \alpha = 2 \sin\alpha\, \cos\alpha,\;[/math]
[math]\cos 2 \alpha = \cos^2\alpha-\sin^2\alpha\;[/math]
oraz połówkowego kąta:
[math] \sin\frac{\alpha}{2} = \sqrt{\frac{1-\cos\alpha}{2}},\ \cos\frac{\alpha}{2} = \sqrt{\frac{1+\cos\alpha}{2}}\;[/math]
Wzory redukcyjne na sprowadzanie kąta do pierwszej ćwiartki
Okresowość funkcji trygonometrycznych oraz wzory na sumę kątów pozwalają sprowadzić dowolny argument funkcji trygonometrycznej do I. ćwiartki.
Przykład
Funkcje odwrotne do funkcji trygonometrycznych
Z uwagi na okresowość funkcji trygonometrycznych, nie można zdefiniować funkcji odwrotnych do nich dla wszystkich argumentów. Funkcję odwrotną do [math]f\;[/math] można zdefiniować dla tych argumentów, dla których [math]f\;[/math] jest wzajemnie jednoznaczna.
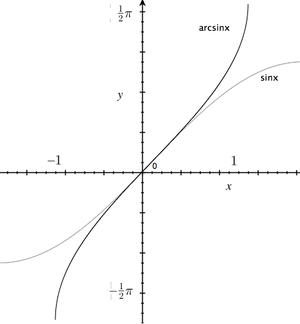
Weźmy funkcję [math]f(x)=\sin x\;[/math] (+ zbiory, pomiędzy którymi [math]f\;[/math] działa). Patrząc na wykres [math]y=f(x)=\sin x\;[/math], widać, że [math]f:X\to Y\;[/math] jest funkcją wzajemnie jednoznaczną, jeśli za zbiór argumentów weźmiemy [math]X=\left [-\frac{\pi}{2},\frac{\pi}{2}\right ]\;[/math], zaś za zbiór wartości [math]Y=[-1,1]\;[/math].
Funkcję odwrotną [math]\sin^{-1}(\cdot)\;[/math] do funkcji [math]\sin(\cdot)\;[/math] nazywamy [math]\arcsin(\cdot)\;[/math] i definiujemy — zgodnie z definicją funkcji odwrotnej — jako: Jeśli [math]y=\sin(x)\;[/math], to [math]x=\sin^{-1}(y)=\arcsin(y)\;[/math].
Uwaga
Wzajemna jednoznaczność [math]\sin:\;[/math] [math]X\to Y\;[/math] ma miejsce także w innych sytuacjach, np. "X niestandardowy": [math]X_{ns}=\left [\frac{\pi}{2},\frac{3\pi}{2}\right ]\;[/math], [math]Y=[-1,1]\;[/math], i zdefiniować funkcję [math]\arcsin_{ns}: [-1,1]\to \left [ \frac{\pi}{2},\frac{3\pi}{2}\right ]\;[/math]. Standardowa umowa mówi, że za [math]X\;[/math] bierze się [math]X=\left [-\frac{\pi}{2},\frac{\pi}{2}\right ]\;[/math].
Funkcja odwrotna do sinusa
Ostatecznie (aby oswoić z różnymi notacjami):
Def. Dla funkcji [math]\sin(\cdot)\;[/math]: [math]\left [-\frac{\pi}{2},\frac{\pi}{2}\right ] \stackrel{\sin}{\to} [-1,1]\;[/math] definiujemy odwrotną do niej funkcję [math]\arcsin(\cdot)\;[/math]: [math][-1,1] \stackrel{\arcsin}{\to} \left [-\frac{\pi}{2},\frac{\pi}{2}\right ] \;[/math] jako: Jeśli [math]y=\sin(x)\;[/math], to [math]x=\arcsin(y)\;[/math] (więc np. [math]\arcsin(1)=\frac{\pi}{2}, \arcsin(\frac{1}{2})=\frac{\pi}{6}\;[/math] itd.).
Wykres funkcji [math]\arcsin\;[/math]
— zgodnie z ogólną reguła uzyskiwania wykresów funkcji odwrotnych — otrzymuje się z wykresu [math]\sin\;[/math] przez zamianę osi lub równoważnie przez symetrię względem osi [math]y=x\;[/math].
Funkcje odwrotne dla innych funkcji trygonometrycznych
Def. Dla funkcji [math]\cos(\cdot)\;[/math]: [math][-[0,\pi] \stackrel{\cos}{\to} [-1,1]\;[/math] definiujemy odwrotną do niej funkcję [math]\arccos(\cdot)\;[/math]: [math][-1,1] \stackrel{\arcsin}{\to} [0,\pi] \;[/math] jako: Jeśli [math]y=\cos(x)\;[/math], to [math]x=\arccos(y)\;[/math].
Def. Dla funkcji [math]\tg(\cdot)\;[/math]: [math]\left ]-\frac{\pi}{2},\frac{\pi}{2}\right [ \stackrel{\tg}{\to} \left ]-\infty,\infty \right [\;[/math] definiujemy odwrotną do niej funkcję [math]{\rm \mathop{arctg}}(\cdot)\;[/math]: [math] \left ]-\infty,\infty \right [ \stackrel{\rm \mathop{arctg}}{\to} \left ]-\frac{\pi}{2},\frac{\pi}{2} \right[ \;[/math] jako: Jeśli [math]y=\tg(x)\;[/math] ,to [math]x={\rm \mathop{arctg}}(y)\;[/math].
Biegunowy układ współrzędnych
Punkt na płaszczyźnie można zaznaczyć, zadając układ współrzędnych i pisząc współrzędne punktu [math]p\;[/math] (w tym układzie są to też składowe wektora [math]\vec{OP}\;[/math]).
Do wyznaczenia położenia punktu na płaszczyźnie można jednak użyć innego układu współrzędnych. Jeżeli zamiast [math](x,y)\;[/math] wprowadzimy [math]r,\phi\;[/math] przez
(lub na odwrót: [math]r=\sqrt{x^2+y^2},\; \phi = {\rm \mathop{arctg}}\frac{y}{x}\;[/math]), to jest to równie dobry układ współrzędnych co [math](x,y)\;[/math]: Każdemu punktowi płaszczyzny odpowiada dokładnie jedna para liczb [math](r,\phi)\;[/math] oraz na odwrót: Każdej parze [math](r,\phi)\;[/math] odpowiada dokładnie jeden punkt płaszczyzny. (jest jeden WYJĄTEK: punkt [math](0,0)\;[/math], gdzie kąt [math]\phi\;[/math] nie jest określony).
Jedną z większych sztuk w matematyce (i fizyce) jest dobór odpowiedniego układu współrzędnych.
Gdy się go odpowiednio (do zagadnienia) dobierze, to problem często znacznie się upraszcza lub nawet trywializuje.
Przykłady
- Równanie okręgu (o środku w [math](0,0)\;[/math] i promieniu [math]R\;[/math]) ma we współrzędnych kartezjańskich postać
[math] x^2+y^2=R^2 \;[/math] zaś we współrzędnych biegunowych
[math] r=R, \;\;\;\;\; \phi - {\rm dowolne.} \;[/math] -
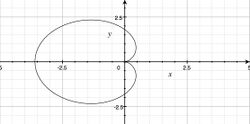
Rozważmy krzywą (kardioidę)
[math] (x^2+y^2 + 2a x)^2=4a^2(x^2+y^2), \;\;\; a\gt 0 \;[/math] Analiza we współrzędnych kartezjańskich, aczkolwiek możliwa, jest dość uciążliwa. We współrzędnych biegunowych badanie jest o wiele łatwiejsze i krzywą można narysować "od ręki".
[math] r=a(1+ \cos\phi) \;[/math] - Rozważmy krzywą (lemniskata Bernoulliego)
[math] (x^2+y^2)^2=2a^2(x^2-y^2), \;\;\; a\gt 0 \;[/math] 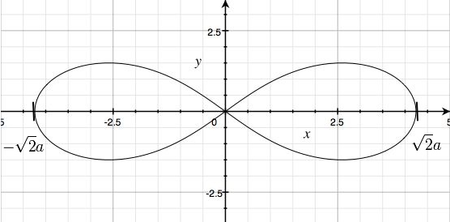 Rysunek wykres leminiskaty Bernoulliego dla a=3
Rysunek wykres leminiskaty Bernoulliego dla a=3Można ją wykreślić we współrzędnych kartezjańskich, aczkolwiek jest to dość pracochłonne. We współrzędnych biegunowych ma ona o wiele dogodniejszą do analizy postać:
[math] r^2=2a^2 \cos 2 \phi \;[/math]
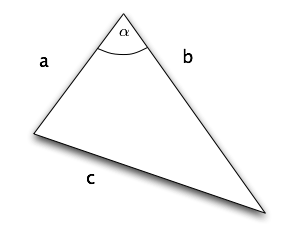
Twierdzenie kosinusów
Rozpatrzmy trójkąt o bokach długości [math]a,b,c\;[/math], gdzie kąt między bokami [math]a\;[/math] i [math]b\;[/math] wynosi [math]\alpha\;[/math]. Ma miejsce następujące uogólnienie twierdzenia Pitagorasa, zwane twierdzeniem kosinusów:
Zachodzi:
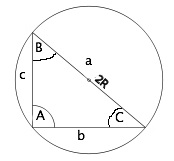
Twierdzenie sinusów
Rozpatrzmy trójkąt o bokach [math]a,b,c\;[/math] oraz kątach: [math]\alpha\;[/math] — naprzeciw boku [math]a\;[/math] (tzn. kąt pomiędzy bokami [math]b\;[/math] i [math]c\;[/math]); [math]\beta\;[/math] — naprzeciw boku [math]b\;[/math]; [math]\gamma\;[/math] — naprzeciw boku [math]c\;[/math]. Między długościami boków [math]a,b,c\;[/math] a kątami [math]\alpha,\beta, \gamma\;[/math] zachodzą następujące związki, zwane twierdzeniem sinusów:
Zachodzą równości:
gdzie [math]R\;[/math] — promień okręgu opisanego na trójkącie.