TI/Zadania dodatkowe

Zadania z rysowania i dopasowania funkcji

Znajdowanie miejsca zerowego funkcji

Wyznaczyć pierwiastek równania [math]x^3 - x + 1 = 0[/math] w przedziale [−2;2] metodą bisekcji. Kolejne kroki algorytmu zilustrować serią wykresów analogicznie do poniższego przykładu.

[...przykład...]

Wczytywanie danych i wykres

W tym zadaniu analizujemy fragment wyników eksperymentu dotyczącego pomiaru stałej Stefana-Boltzmanna. W eksperymencie tym walec polerowany i okopcony podgrzewane są grzałkami dostarczającymi jednakową moc każdemu z nich. Dla pewnej temperatury walców ustala się równowaga pomiędzy ilością energii dostarczanej przez grzałkę a ilością energii wypromieniowywanej przez walec. Temperatura ta jest zależna od współczynnika promieniowania ciała. Jak można się domyśleć, ciało, które promieniuje więcej, będzie mieć niższą temperaturę przy tej samej mocy dostarczanej przez grzałkę.

Plik Plik:Seria I.txt zawiera trzy kolumny danych. Dane te to odpowiednio: kolejne chwile czasu (mierzonego w minutach) oraz pomiary temperatury walca polerowanego i okopconego.

Proszę:

• zapisać plik w bieżącym katalogu;
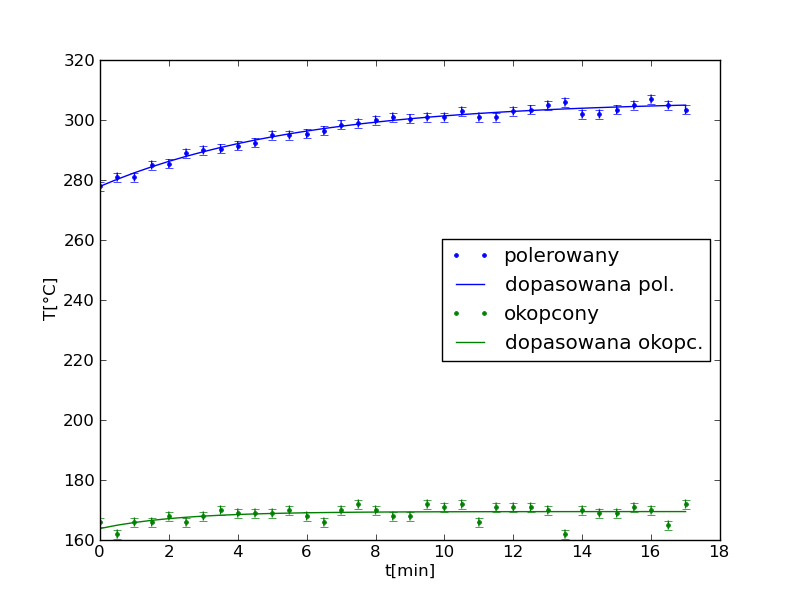
• korzystając z funkcji dostępnych w module pylab wykreślić dane tak aby uzyskać rysunek analogiczny do poniższego:

.

Dopasowywanie krzywej do danych i wykres

W poprzednim zadaniu rozważaliśmy dochodzenie walców do równowagi termicznej. Proces ten teoretycznie powinien przebiegać w czasie zgodnie z funkcją: [math]T(t) = T_R + A e^{-\frac{t}{\tau}},[/math] gdzie: [math] T_R[/math] — temperatura równowagi, [math]A[/math] — pewien parametr, [math]\tau[/math] — stała czasowa dochodzenia do równowagi. Te trzy wartości nazywamy parametrami poszukiwanej funkcji. Mając zebrane punkty doświadczalne, czyli zestaw wartości t i T(t), możemy spróbować z nich wyznaczyć nieznane parametry T_R, A oraz [math]\tau[/math]. Procedurę taką nazywamy dopasowaniem krzywej do punktów doświadczalnych.

Poniższe wskazówki pokazują jak uzyskać pożądane wyniki dla walca polerowanego. Do danych z poprzedniego zadania proszę rozwinąć przykładowy kod tak aby dla walca czarnego:

• dopasować krzywą opisaną powyższym równaniem;
• wypisać wartości otrzymanych parametrów i ich standardowe odchylenia;
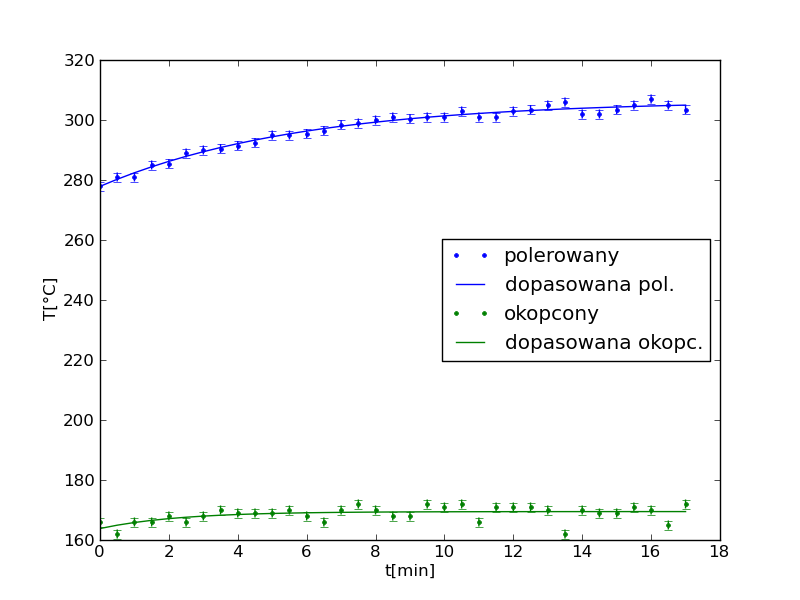
• wykreślić otrzymane krzywe teoretyczne na tle punktów z zaznaczonymi błędami tak jak przedstawia to poniższy rysunek:

Wskazówki

Ponieważ zagadnienia dopasowywania parametrów krzywych wybiegają poza zakres materiału tych ćwiczeń, poniżej podajemy kody przydatnych do tego celu funkcji. Generalnie metoda polega na takim modyfikowaniu wartości dopasowywanych parametrów, aby zminimalizować rozbieżność pomiędzy wartościami funkcji obliczonymi ze wzoru teoretycznego a odpowiadającymi im wartościami zmierzonymi w eksperymencie. Rozbieżność tę (w postaci sumy kwadratów różnic w każdym punkcie doświadczalnym) oblicza w poniższym kodzie funkcja funkcja_bledu, zaś za odpowiednie modyfikacje parametrów, prowadzące do zmniejszenia sumy kwadratów rozbieżności, odpowiada funkcja leastsq z modułu scipy.optimize. Funkcja ta jest wykorzystywana wewnątrz funkcji dopasuj w poniższym kodzie. Funkcja dopasuj zwraca krotkę zawierającą tablicę dopasowanych parametrów i tablicę odpowiadających im standardowych odchyleń.

Postać zależności teoretycznej zapisujemy w osobnej funkcji. W podanym poniżej przykładzie jest to moja_fun.

# -*- coding: utf-8 -*-
import numpy as np
import pylab as py

################## definicje potrzebne do dopasowania ################
import scipy.optimize as opt
def funkcja_bledu( b, x, y, err,funkcja):
    '''Suma kwadratów tej funkcji jest minimalizowana w
    procesie optymalizacji parametrów'''
    y_fit = funkcja(b, x) 
    residuum = y-y_fit 
    residuum_wazone = residuum / err 
    return residuum_wazone

def dopasuj(x,y,err,b_init,fun):
    '''
    funkcja fun definiuje pewną zależność między x i y: y = fun(x;b),
    która zależy od pewnych parametrów b. Zakładamy, że wartości y znane są
    z błędem err. b_init zawiera początkowe zgadnięte (np. przez popatrzenie na wykres)
    wartości parametrów b.
    Funkcja dopasuj znajduje wartości parametrów b, dla których suma kwadratów wartości
    funkcji dopasowanej i wartości zmierzonej dla danego x_i jest najmniejsza.

    UWAGA: Jak większość procedur minimalizacyjnych, używana w tej funkcji procedura
    jest wrażliwa na punkt startowy, tzn. dla różnych wartości startowych b_init
    możemy dostać różne rozwiązania 
    '''

    out = opt.leastsq(funkcja_bledu, b_init, args=(x,y,err,fun), full_output=1)

    # funkcja opt.leastsq tak zmienia parametry b 
    # aby suma kwadratów wartości zwracanych przez funkcja_bledu była jak najmniejsza

    # odczytujemy wyniki minimalizacji
    b_final = out[0]
    covar = out[1]
    std_b = (np.diag(covar))**0.5 
    return (b_final, std_b)

####################################################################

def moja_fun(b,t):
    T = b[0] + b[1]*np.exp(-t/b[2])
    return T

# wczytanie danych ...
a = np.loadtxt('seria_I.txt')
t = a[:,0]
Tp = a[:,1]
Tc = a[:,2]
sigma = 1.5

# DOPASOWANIE DLA WALCA POLEROWANEGO
# musimy podać wartości startowe dla procedury minimalizacji 
b_init = [300.0, -1.0, 10.0]
(parametry_p, std_bl)=dopasuj(t,Tp,sigma,b_init,moja_fun)
print 'temperatura równowagi: ', parametry_p[0],'jej standardowe odchylenie:', std_bl[0]

# TERAZ WYKONUJEMY ANALOGICZNE DOPASOWANIE DLA WALCA CZARNEGO ...
# ...

# RYSUNEK
wp = py.errorbar(t,Tp, yerr=sigma, fmt='b.')
fp = py.plot(t,moja_fun(parametry_p,t))

# ....

py.legend((wp[0],fp,wc[0],fc),('polerowany','dopasowana pol.','okopcony','dopasowana okopc.'),'center right')

# ....