Elektrodynamika/Seria 1
Elektrodynamika dla Neuroinformatyki
Seria 1
Spis treści
Zadanie 1
Wyprowadzić wzór, umożliwiający obliczenie gradientu we współrzędnych sferycznych.
Zadanie 2
Znaleźć wektor natężenia pola elektrycznego w odległości [math] z [/math] od środka cienkiego pręta o długości [math] 2L [/math] naładowanego ze stałą gęstością liniową [math] \lambda [/math]. Jak wynik zmieni się, gdy wyznaczymy ten wektor w odległości [math] z [/math] od jednego z końców pręta? Skomentować wyniki dla dużych odległości.
Zadanie 3
Znaleźć potencjał w całej przestrzeni pochodzący od cienkiej, nieskończonej nici naładowanej ze stałą gęstością liniową [math] \lambda [/math].
Zadanie 4
Znaleźć wektor natężenia pola elektrycznego [math]\vec{E}[/math] na osi cienkiego krążka o promieniu R, naładowanego jednorodnie z powierzchniową gęstością ładunku [math]\sigma [/math]. Korzystając z równania:
- [math]\vec{E} = - \bigtriangledown \phi [/math]
wyznaczyć wartość potencjału elektrycznego [math]\phi [/math] na tej osi. Następnie zastosować postępowanie odwrotne, tj. wyznaczyć potencjał na osi pierścienia, po czym korzystając z wyniku, przejść do wektora pola elektrycznego. Wynik skomentować.
Zadanie 5
Znależć wektor natężenia pola elektrycznego [math]\vec{E}[/math] w odległości z od powierzchni kulistej o promieniu R, naładowanej jednorodnie z gęstością powierzchniową [math]\sigma [/math].Rozważyć przypadek [math]z\lt R[/math] (wewnątrz kuli) oraz [math]z\gt R[/math] (na zewnątrz kuli). Wynik wyrazić poprzez całkowity ładunek Q zgromadzony na powierzchni kuli.
Zadanie 6
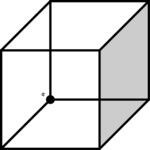
Ładunek [math] q [/math] umieszczony został w jednym z wierzchołków sześcianu o boku długości [math] a [/math], jak przedstawiono na rysunku. Znaleźć wartość strumienia pola elektrycznego przez zacieniowaną ściankę. Jaki byłby wynik, gdyby strumień policzyć przez powierzchnię całego sześcianu?