Funkcje ciągłe
Funkcja ciągła
Mówimy, że funkcja [math]f\;[/math] jest ciągła w punkcie [math]a\;[/math], jeśli spełniony jest warunek
Przypominając sobie definicję granicy funkcji [math]f\;[/math] w punkcie [math]a\;[/math] można więc powiedzieć, że dla funkcji [math]f\;[/math] ciągłej w punkcie [math]a\;[/math] mamy:
Dla dowolnego ciągu {[math]x_n[/math]} takiego, że [math]\displaystyle\mathop{\lim}_{n\to\infty} \,x_n=a\;[/math] zachodzi
Jeśli w równości (1) zastąpić granicę przez granicę jednostronną, to otrzymamy definicję ciągłości jednostronnej:
Granica jednostronna
Mówimy, że funkcja [math]f\;[/math] jest prawostronnie (lewostronnie) ciągła w punkcie [math]a\;[/math], jeśli
Jeśli funkcja [math]f\;[/math] jest określona nie dla wszystkich [math]x\;[/math], dla których określona jest granica, to w powyższych definicjach ograniczamy zakres zmienności [math]x\;[/math] do zbioru argumentów funkcji.
I tak np. jeśli [math]f\;[/math] jest określona na odcinku domkniętym [math][a,b]\;[/math], to ciągłość [math]f[/math] w punkcie [math]a\;[/math] oznacza jedynie jej ciągłość prawostronną, ciągłość w punkcie [math]b\;[/math] — ciągłość lewostronną.
Funkcja ciągła na odcinku
Funkcję ciągłą dla każdej wartości argumentu ze zbioru [math]X\;[/math] nazywamy funkcją ciągłą na [math]X\;[/math].
I tak np. mówiąc, że funkcja [math]f\;[/math] jest ciągła na odcinku domkniętym [math][a,b]\;[/math] mamy na myśli, że jest prawostronnie ciągła w punkcie [math]a\;[/math], lewostronnie ciągła w punkcie [math]b\;[/math] oraz obustronnie ciągła w punktach wewnętrznych odcinka [math][a,b]\;[/math].
Funkcja ciągła przedziałami
Mówimy, że funkcja [math]f\;[/math] jest przedziałami ciągła na odcinku [math][a,b]\;[/math], jeśli ten odcinek można podzielić za pomocą skończonego układu punktów [math]a_0,a_1, a_2, \dots, a_n\;[/math], gdzie
na podprzedziały [math][a_{k-1},a_k]\;[/math] ([math]k=1,2,\dots, n\;[/math]) w taki sposób, że wewnątrz każdego przedziału funkcja [math]f\;[/math] jest ciągła i istnieją granice jednostronne [math]\lim_{x \to a_{k-1}^+}{f(x)},[/math] i [math]\lim_{x \to a_k^-}{f(x)},[/math].
Innymi słowy, funkcja posiadająca skończoną ilość punktów nieciągłości, w których istnieją obie granice jednostronne, jest funkcją przedziałami ciągłą.
Przykłady
- Pokazaliśmy niedawno, że [math]\displaystyle\mathop{\lim}_{x\to {0}}x^2=0\;[/math]. Znaczy to, że funkcja [math]f(x)=x^2\;[/math] jest ciągła w punkcie [math]x=0\;[/math] (jest też ciągła na całym zbiorze [math]\mathbb R\;[/math], co niedługo pokażemy).
- Funkcja [math]f(x)=[x]\;[/math] (patrz wykres) jest nieciągła w punktach całkowitych. Dokładniej, w tych punktach jest ciągła prawostronnie, lecz nie lewostronnie. Ponieważ jednak granice lewostronne istnieją, to jest przedziałami ciągła na dowolnym odcinku skończonym.Plik:Floor function.svgFunkcja schodkowa
- Funkcja [math]f(x)=\sin\left(\frac{1}{x}\right)\;[/math] ma nieokreśloną wartość w punkcie [math]x=0\;[/math]. Dookreślmy ją tam, definiując: [math]f(0)=0\;[/math]. Nawet tak dookreślona funkcja jest nieciągła w [math]x=0\;[/math], ponieważ nie istnieją granice (lewo- ani prawostronne) w tym punkcie.
- Funkcja Dirichleta jest nieciągła w każdym punkcie.
Warunek ciągłości Cauchy'ego
Twierdzenie poniżej może być przyjęte jako definicja ciągłości funkcji (definicja Cauchy'ego). Jest ona równoważna definicji Heinego. Ta równoważność jest konsekwencją twierdzenia o równoważności warunków istnienia granic funkcji: Cauchy'ego i Heinego.
Twierdzenie
Warunkiem koniecznym i dostatecznym na to, aby funkcja [math]f\;[/math] była ciągła w punkcie [math]a\;[/math], jest, aby
Można to wyrazić bardziej obrazowo mówiąc, że dostatecznie małym przyrostom zmiennej niezależnej odpowiadają tak małe, jak tylko się chce, przyrosty wartości funkcji. Można to zapisać następująco (po ostatnim kwantyfikatorze w wyrażeniu powyżej):
Inna postać twierdzenia
Jeszcze inaczej: Funkcja [math]f\;[/math] jest ciągła w punkcie [math]a\;[/math], jeżeli
Uwaga
Ciągłość funkcji w punkcie jest własnością lokalną: Aby zbadać, czy funkcja jest ciągła w punkcie [math]a\;[/math], wystarczy znać znać tę funkcję w dowolnie małym otoczeniu [math]a\;[/math].
Ciągłość funkcji elementarnych
Z wzorów na działania na granicach funkcji wynika od razu, że działania arytmetyczne wykonywane na funkcjach ciągłych dają w wyniku funkcje ciągłe. Innymi słowy: Jeśli funkcje [math]f\;[/math], [math]g\;[/math] są ciągłe w punkcie [math]a\;[/math], to ich suma, różnica, iloczyn, iloraz (jeśli [math]g(a)\ne 0\;[/math]) są również ciągłe w punkcie [math]a[/math].
Zróbmy teraz mały katalog funkcji ciągłych:
- Funkcja stała [math]f(x)=const.\;[/math] i funkcja [math]f(x)=x\;[/math] są funkcjami ciągłymi, co widać od razu z definicji.
- Stąd oraz z twierdzenia o ciągłości iloczynu i sumy funkcji ciągłych wynika, że wielomiany są funkcjami ciągłymi.
- Stąd oraz z twierdzenia o ciągłości ilorazu funkcji ciągłych wynika, że funkcje wymierne [math]f(x)=\frac{P(x)}{Q(x)}\;[/math] są funkcjami ciągłymi w tych punktach, gdzie [math]Q(x)\ne 0\;[/math]
- Ciągłość funkcji wykładniczej [math]a^x\;[/math], [math]a\gt 0\;[/math]. Najsampierw pokażemy, że
[math] \displaystyle\mathop{\lim}_{x\to {0}} a^x=1. [/math] Pamiętamy bowiem granicę dla ciągów:
[math] \displaystyle\mathop{\lim}_{n\to\infty} a^\frac{1}{n} =1. [/math]
Stąd wynika, że również
[math] \displaystyle\mathop{\lim}_{n\to\infty} a^{-\frac{1}{n}} = \frac{1}{\displaystyle\mathop{\lim}_{n\to\infty} a^\frac{1}{n}}=1. [/math]
Dlatego też, dla dowolnego [math]\epsilon\gt 0\;[/math] można znaleźć wskaźnik [math]N\;[/math] taki, że (dla [math]a\gt 1\;[/math])
[math] 1-\epsilon\lt a^{-\frac{1}{N}}\lt a^{\frac{1}{N}}\lt 1+\epsilon [/math]
Jeżeli teraz weźmiemy takie [math]x\;[/math], że [math]|x|\lt \frac{1}{N}\;[/math], (czyli [math]-\frac{1}{N}\lt x\lt \frac{1}{N}\;[/math]), to mamy
[math] a^{-\frac{1}{N}}\lt a^x\lt a^{\frac{1}{N}} [/math]
skąd
[math] 1-\epsilon\lt a^x\lt 1+\epsilon \Longrightarrow |a^x-1|\lt \epsilon [/math]
a to oznacza, że [math]\displaystyle\mathop{\lim}_{x\to {0}} a^x=1.\;[/math]
Teraz! Weźmy dowolne [math]x\;[/math].
Mamy: [math]a^{x+h}-a^x = a^x(a^h-1)[/math] oraz [math]\lim_{h\to 0} a^h = 1[/math], skąd [math]\lim_{h\to 0} (a^{x+h}-a^x) = 0\,[/math], co zgodnie z wersją warunku ciągłości (3) oznacza, że funkcja [math]a^x\;[/math] jest ciągła w dowolnym punkcie [math]x\;[/math].
Ciągłość funkcji trygonometrycznych
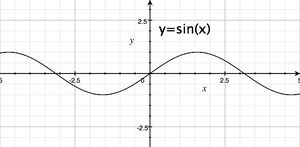
Przypominając sobie definicję funkcji [math]\sin x\;[/math] (RYS) mamy nierówność (dla [math]x\gt 0\;[/math]):
[math] 0 \lt \sin x \lt x [/math]
Stąd, na mocy twierdzenia o granicach trzech funkcji, wynika, że
(ściśle rzecz biorąc, powyższa granica jest granicą prawostronną; ale z antysymetrii funkcji sin wynika również ta sama równość dla granicy lewostronnej). Równość (4) znaczy też, że funkcja [math]\sin x\;[/math] jest ciągła w [math]x=0\;[/math].
Znając granicę (4) łatwo pokażemy, że
[math] \displaystyle\mathop{\lim}_{x\to {0}} \cos x = 1. [/math]
Mamy bowiem: [math]1-\cos x = 2 \sin^2\frac{x}{2}\lt 2\sin\frac{x}{2}\lt x\;[/math], co — na mocy twierdzenia o granicach trzech funkcji — oznacza, że [math]\displaystyle\mathop{\lim}_{x\to {0}}(1-\cos x)=0\;[/math].
Mamy też w ten sposób ustanowioną ciągłość funkcji [math]\cos x\;[/math] w zerze.
Teraz pokażemy, że funkcje: [math]\sin x\;[/math] i [math]\cos x\;[/math] są wszędzie ciągłe, korzystająctu z warunku (3).
Mamy bowiem:
[math] \sin(x+h)-\sin x = 2 \sin\frac{h}{2} \cos\left(x+\frac{h}{2}\right) [/math]
i, korzystając z nierówności: [math]|\sin x|\leq |x|\;[/math] oraz [math]|\cos x|\leq 1\;[/math], mamy
[math] |\sin(x+h)-\sin x|\leq |h| \Longrightarrow \lim_{h \to 0} |\sin(x+h)-\sin x| = 0 [/math]
czyli
[math] \lim_{h \to 0} \sin(x+h)-\sin x = 0. [/math]
Podobnie
[math] |\cos(x+h)-\cos x|=2\left|\sin\frac{h}{2}\right|\cdot \left|\sin\left(x+\frac{h}{2}\right)\right| \leq |h| [/math]
co daje
Wniosek
Funkcja [math]\tg x=\frac{\sin x}{\cos x}\;[/math] jest ciągła dla [math]x\ne \frac{\pi}{2}+k\pi\;[/math], a [math]\ctg x\;[/math] — dla [math]x\ne k\pi\;[/math] (tu [math]k\in\mathbb Z\;[/math]).
Ciągłość logarytmu i funkcji cyklometrycznych
Do kompletu funkcji elementarnych trzeba by jeszcze pokazać ciągłość logarytmu oraz funkcji cyklometrycznych (odwrotnych do funkcji trygonometrycznych). Zrobimy to za chwilę, kiedy pokażemy ciągłość funkcji odwrotnych do ciągłych. Na razie zaś będziemy potrzebować:
Twierdzenie
Jeśli [math]\displaystyle\mathop{\lim}_{x\to {a}} f(x)=A\;[/math] i [math]\lim_{y \to A}g(y)=B\;[/math], to [math]\displaystyle\mathop{\lim}_{x\to {a}} g(f(x))=B\;[/math].
Dowód
Niech [math]\displaystyle\mathop{\lim}_{n\to\infty} x_n=a\;[/math]; mamy wtedy [math]\displaystyle\mathop{\lim}_{n\to\infty} f(x_n)=A\;[/math]. Weźmy [math]y_n=f(x_n)\;[/math]. Mamy [math]\displaystyle\mathop{\lim}_{n\to\infty} y_n=A\;[/math], zatem [math]\displaystyle\mathop{\lim}_{n\to\infty} g(y_n)=B = \displaystyle\mathop{\lim}_{n\to\infty} g(f(x_n))\;[/math], a to znaczy, że [math]\lim_{x \to \infty} g(f(x))=B\;[/math].
CBDO
Twierdzenie — superpozycja dwóch funkcji ciągłych jest funkcją ciągłą
Korzystając z tego, pokażemy, że superpozycja (złożenie) dwóch funkcji ciągłych jest funkcją ciągłą. Dokładniej:
Tw.Jeśli funkcja [math]y=f(x)\;[/math] jest ciągła w punkcie [math]x=a\;[/math], zaś funkcja [math]z=g(y)\;[/math] jest ciągła w punkcie [math]y=f(a)\;[/math], to funkcja [math]g(f(x))\;[/math] jest ciągła w punkcie [math]x=a\;[/math].
Dowód
Weźmy ciąg {[math]x_n[/math]} taki, że [math]\displaystyle\mathop{\lim}_{n\to\infty} x_n=a\;[/math]. Mamy wtedy [math]\displaystyle\mathop{\lim}_{n\to\infty} f(x_n)=f(a)\;[/math]. Biorąc [math]b=f(a)[/math] i [math]y_n=f(x_n)[/math] mamy [math]\displaystyle\mathop{\lim}_{n\to\infty} y_n=b\;[/math], skąd — wykorzystując z kolei ciągłość funkcji [math]g[/math]:
CBDO
Przykład
Przywoływana tu kilkakrotnie funkcja [math]\sin\left(\frac{1}{x}\right)\;[/math] jest ciągła we wszystkich punktach poza [math]x = 0[/math].
Niektóre ogólne własności funkcji ciągłych
Ciągłość jednostajna
Mówimy, że funkcja [math]f\;[/math] jest ciągła jednostajnie na zbiorze X, jeśli
Uwaga I
Zauważmy, że definicja ciągłości zwykłej mówiła o ciągłości funkcji w punkcie, natomiast definicja ciągłości jednostajnej mówi o ciągłości funkcji na zbiorze.
Uwaga II
Porównując to z definicją ciągłości funkcji [math]f\;[/math] w punkcie [math]x\;[/math]:
widać następujące różnice: W definicji ciągłości zwykłej, delta {\em mogła zależeć od wybranego [math]\epsilon\;[/math] oraz [math]x\;[/math]}. W definicji ciągłości jednostajnej, delta może zależeć tylko od [math]\epsilon\;[/math], musi zaś być taka sama dla wszystkich [math]x\in X\;[/math].
Przykład I
Rozważmy funkcję [math]f(x)=x^2\;[/math] na zbiorze [math]X_1=[0,1]\;[/math] i na zbiorze [math]X_2=[0,\infty[\;[/math].
Na obu tych zbiorach jest oczywiście ciągła w zwykłym sensie.
Co do ciągłości jednostajnej, to [math]f(x)\;[/math] jest ciągła jednostajnie na [math]X_1\;[/math] (wystarczy wziąć [math]\delta = \frac{\epsilon}{3}\;[/math] przy sprawdzaniu warunku (5)), natomiast nie jest ciągła jednostajnie na [math]X_2\;[/math]. Weźmy bowiem np. [math]\epsilon=1\;[/math] i jakiekolwiek [math]\delta\;[/math]. Wtedy [math]x'=x+\frac{1}{2}\delta\;[/math] i mamy: [math]f(x)-f(x')= x\delta+\frac{1}{4}\delta^2\;[/math], co można uczynić dowolnie dużym przez odpowiedni dobór [math]x\;[/math] — tu wystarczy wziąć [math]x=\frac{1}{\delta}\;[/math].
Przykład II
Funkcja [math]f{x}=\frac{1}{x}\;[/math] jest ciągła na zbiorze [math]X=]0,1]\;[/math], natomiast nie jest tam jednostajnie ciągła.
Następujące twierdzenie mówi o tym, że taka sytuacja nie może się zdarzyć dla funkcji ciągłych na odcinku domkniętym.
Twierdzenie o ciągłości jednostajnej
Funkcja ciągła na odcinku domkniętym [math][a,b]\;[/math] jest też na nim jednostajnie ciągła.
Dowód
będzie się odbywał przez sprowadzenie do niedorzeczności (tzn. przyjmijmy, że prawdziwe jest zaprzeczenie tezy, i jako konsekwencję otrzymamy sprzeczność). Przyjmijmy więc, że istnieje [math]\epsilon\gt 0\;[/math] takie, że dla każdego [math]\delta\gt 0\;[/math] istnieje para argumentów [math]x,x'\;[/math] takich że
W szczególności, biorąc [math]\delta=\frac{1}{n}\;[/math], wnioskujemy, że istnieją takie dwa ciągi [math]\{x_n\}.[/math] i [math]\{x'_n\}.[/math], że
Ponieważ ciąg [math]{\{x_n}\}.[/math] jest ograniczony, zatem — na podstawie tw. Bolzano-Weierstrassa — zawiera podciąg zbieżny [math]\{x_{m_n}\}.[/math].
Oznaczmy jego granicę jako [math]c\;[/math]: [math]\displaystyle\mathop{\lim}_{n\to\infty} {x_m}_n=c\;[/math]. Z pierwszej z nierówności (6) mamy: [math]a\leq c \leq b\;[/math].
Funkcja [math]f\;[/math] z założenia jest ciągła wszędzie na [math][a,b]\;[/math], więc także w punkcie [math]c\in [a,b]\;[/math]. Mamy więc:
[math]\lim_{n \to \infty} f(x_{m_n} = f(c))\;[/math]. Ale teraz: Rozważmy podciąg ciągu
{[math]x'_n[/math]} o tych samych numerach, co podciąg {[math]x_m[/math]}, tzn. [math]\{x'_{m_n}\}.[/math].
Z trzeciej z nierówności (6) wynika, że również [math]\{x'_{m_n}\}.[/math] dąży do tej samej granicy:
[math]\displaystyle\mathop{\lim}_{n\to\infty} {x'_{m_n}}=c\;[/math], bo [math]\displaystyle\mathop{\lim}_{n\to\infty} {x'_{m_n}} =\displaystyle\mathop{\lim}_{n\to\infty} {x_{m_n}}\;[/math]. Ciągłość funkcji [math]f\;[/math] jak poprzednio daje:
[math]\lim_{n \to \infty} f(x'_{m_n} = f(c))[/math]. A zatem:
[math]\lim_{n \to \infty} (f(x'_{m_n}) - f(x_{m_n}) = 0)\;[/math]
Ale to jest sprzeczne z ostatnią z nierówności (6).
CBDO
Twierdzenie Weierstrassa
Funkcja [math]f\;[/math] ciągła w przedziale domkniętym [math][a,b]\;[/math] jest ograniczona, a ponadto osiąga tam swoje kresy: dolny [math]m=\mathop{\inf}_{x\in [a,b]} f(x)\;[/math] oraz górny [math]M=\mathop{\sup}_{x\in [a,b]} f(x)\;[/math]. Innymi słowy, istnieją w tym przedziale takie dwa punkty [math]c\;[/math] i [math]d\;[/math], że [math]f(c)=m\;[/math] oraz [math]f(d)=M\;[/math].
Dowód
Pokażemy najsampierw, że funkcja [math]f\;[/math] jest ograniczona, tzn. [math]\exists_A: \forall_{x\in [a,b]}: |f(x)|\lt A\;[/math]. Otóż z poprzedniego twierdzenia (o ciągłości jednostajnej) wnioskujemy, że: Wziąwszy np. [math]\epsilon=1\;[/math] istnieje takie [math]\delta\gt 0\;[/math], że jeśli punkty [math]x,x'\;[/math] należą do przedziału o długości mniejszej o [math]\delta\;[/math], to [math]|f(x)-f(x')|\lt 1\;[/math]. Weźmy [math]n\;[/math] takie, aby zachodziła nierówność: [math]\frac{b-a}{n}\lt \delta\;[/math]. W ten sposób, jeśli podzielimy przedział [math][a,b]\;[/math] na [math]n\;[/math] części, to długość każdego z nich jest mniejsza od [math]\delta\;[/math]. Oznaczmy przez [math]a_0, a_1, \dots, a_n\;[/math] końce tych przedziałów, przy czym [math]a_0=a\;[/math], [math]a_n=b\;[/math]. rys. W ten sposób mamy: dla [math]a_0\leq x\leq a_1\;[/math]: [math]|f(x)-f(a_1)|\lt 1\;[/math], skąd [math]|f(x)|\leq 1+|f(a_1)|\;[/math]; i ogólnie, w [math]k\;[/math]-tym przedziale: dla [math]a_{k-1}\leq x\leq a_k\;[/math] [math]|f(x)-f(a_k)|\lt 1\;[/math],skąd [math]|f(x)|\leq 1+|f(a_k)|\;[/math].
Oznaczmy przez [math]A\;[/math] największą z liczb ze zbioru [math]\{ 1+ |f(a_k)|\}\;[/math], [math]k\in \{1, 2, \dots, n\}\;[/math]. Mamy w ten sposób: [math]|f(x)|\lt A\;[/math] dla dowolnego [math]x\in [a,b]\;[/math]. W ten sposób pokazaliśmy, że funkcja [math]f\;[/math] jest ograniczona (tzn. zbiór wartości tej funkcji jest ograniczony). Istnieją więc kresy: górny i dolny tego zbioru.
Pokażemy teraz — przez sprowadzenie do niedorzeczności — że [math]M\;[/math] jest jedną z wartości funkcji, tzn. [math]M=f(d)\;[/math] dla pewnego [math]d\in [a,b]\;[/math]. Przypuśćmy więc, że jest to nieprawda, tzn. [math]\forall_{x\in [a,b]}: M-f(x)\ne 0\;[/math]. Skoro tak, to funkcja
jest określona na całym przedziale [math][a,b]\;[/math] i jest w tym przedziale ciągła. Jest to więc — zgodnie z tym co pokazaliśmy przed chwilą — funkcja ograniczona. Istnieje więc takie [math]N\;[/math], że [math]\forall_{x\in [a,b]}\;[/math]: [math]g(x)\lt N\;[/math], czyli [math]M-f(x)\gt \frac{1}{N}\;[/math], lub w innej formie: [math]f(x)\lt M-\frac{1}{N}\;[/math].
Ale jest to sprzeczne z założeniem, że [math]M\;[/math] jest kresem górnym zbioru wartości funkcji [math]f\;[/math] na [math][a,b]\;[/math].
Dla kresu dolnego dowód jest analogiczny.
CBDO
Twierdzenie (własność Darboux)
Funkcja ciągła w przedziale domkniętym [math][a,b]\;[/math] przyjmuje w tym przedziale wszystkie wartości pośrednie. Innymi słowy: Jeśli [math]f(a)\lt y\lt f(b)\;[/math] lub [math]f(a)\gt y\gt f(b)\;[/math]) to [math]\exists_{c\in [a,b]}: f(c)=y\;[/math].
Dowód
Załóżmy, że [math]f(a)\lt y\lt f(b)\;[/math] (gdy [math]f(b)\lt y\lt f(a)\;[/math], dowód jest analogiczny). Przypuśćmy, że twierdzenie jest fałszywe, a w/ęc, że [math]\forall_{x\in [a,b]}: y-f(x)\ne 0\;[/math]. Zdefiniujmy funkcję [math]h(x)=\frac{1}{|y-f(x)|}\;[/math]; jest ona określona na całym [math][a,b]\;[/math], a ponadto — na mocy twierdzenia Weierstrassa — ograniczona. Niech [math]h(x)\lt M\;[/math], tzn.
Podstawiając w twierdzeniu o ciągłości jednostajnej [math]\epsilon=\frac{1}{M}\;[/math] wnioskujemy, że istnieje [math]\delta\gt 0\;[/math] takie, że dla dowolnych punktów [math]x,x'\;[/math] należących do przedziału o długości mniejszej niż [math]\delta\;[/math], zachodzi
Niech [math]n\;[/math] oznacza liczbę naturalną taką, że [math]\frac{b-a}{n}\lt \delta\;[/math]. Podzielmy odcinek [math][a,b]\;[/math] na [math]n\;[/math] równych części. W oznaczeniach z poprzedniego twierdzenia mamy
Ponieważ [math]f(a_0)=f(a)\lt y\lt f(a_n)=f(b)\;[/math], więc wśród liczb [math]1,2,\dots,n\;[/math] istnieje taka najmniejsza liczba [math]m\;[/math], że [math]y\lt f(a_m)\;[/math]. Mamy więc [math]m\gt 0\;[/math] oraz
(ostatnia nierówność wynika z (8)), co jednak przeczy (7).
CBDO
Twierdzenie
Zestawiając dwa poprzednie twierdzenia, możemy powiedzieć, że zachodzi następujące
Tw.Funkcja ciągła w przedziale domkniętym [math][a,b]\;[/math] przyjmuje wszystkie wartości od kresu dolnego [math]m\;[/math] do kresu górnego [math]M\;[/math], włącznie z [math]m\;[/math] i [math]M\;[/math]. Innymi słowy, zbiorem wartości funkcji jest przedział [math][m,M]\;[/math].
Uwaga
Własność Darboux wdzięcznie ilustruje się rysunkowo. Jednak ciągłość funkcji nie jest warunkiem koniecznym, aby ta własność miała miejsce; zachodzi ona również dla niektórych funkcji nieciągłych.
Przykład I
Jak z wł. Darboux wynika istnienie pierwiastków rzeczywistych równania: [math]x^{2k+1}+a_{2k} x^{2k}+ \dots + a_0=0\;[/math].
Ciągłość funkcji odwrotnych
Niech [math]X,Y\;[/math] — zbiory. Wiadomo, że jeśli [math]f:X\to Y\;[/math] jest bijekcją, to istnieje funkcja odwrotna [math]f^{-1}: Y\to X\;[/math].
Pokażemy teraz, że funkcja odwrotna do funkcji ciągłej jest ciągła. Dokładniej, zachodzi następujące
Twierdzenie
Jeśli funkcja [math]f:[a,b]\to [A,B]\;[/math] jest ciągłą bijekcją, to funkcja odwrotna [math]g\equiv f^{-1}: [A,B]\to [a,b]\;[/math] też jest ciągła.
Uwaga
Z tw.Weierstrassa wiemy, że [math]A= m=\mathop{\inf}_{x\in [a,b]} f(x)\;[/math] oraz [math]B=M=\mathop{\sup}_{x\in [a,b]} f(x)\;[/math].
Dowód
Niech [math]m\leq c \leq M\;[/math]. Na mocy ostatniego Twierdzenia, funkcja [math]f\;[/math] jest określona w punkcie [math]c\;[/math].
Niech [math]c=\displaystyle\mathop{\lim}_{n\to\infty} y_n\;[/math], gdzie [math]\{ y_n \}[/math] należy do przedziału [math][m,M]\;[/math], tzn. jest postaci [math]y_n=f(x_n)\;[/math].
Trzeba pokazać, że [math]\displaystyle\mathop{\lim}_{n\to\infty} g(y_n)=g(c)\;[/math].
Przeformułujmy to w następujący sposób: Niech [math]c=f(d)\;[/math]. Trzeba pokazać, że warunek [math]\displaystyle\mathop{\lim}_{n\to\infty} f(x_n)=f(d)\;[/math] pociąga za sobą [math]\displaystyle\mathop{\lim}_{n\to\infty} x_n=d\;[/math] (bo [math]g(y_n)=x_n, g(c)=d\;[/math]). Ciąg {[math]x_n[/math]} jest ograniczony, jako leżący w przedziale [math][a,b]\;[/math]. Jeśli tak, to można wybrać z niego podciąg zbieżny [math]\{x_k\}[/math]. Niech [math]\displaystyle\mathop{\lim}_{n\to\infty} x_{k_n} =d'\;[/math]. Wykażemy, że [math]d'=d\;[/math]. Z ciągłości funkcji [math]f\;[/math] wynika, że [math]\displaystyle\mathop{\lim}_{n\to\infty} f(x_{k_n})=f(d')\;[/math]. Ponieważ zaś
(w drugiej równości korzystaliśmy z twierdzenia, że jeśli ciąg [math]\{a\}[/math] jest ograniczony i jeśli wszystkie jego podciągi zbieżne są zbieżne do tej samej granicy [math]G\;[/math], to również sam ciąg [math]\{ a_n \}[/math] jest zbieżny do [math]G\;[/math]) więc [math]f(d')=f(d)\;[/math]. Ponieważ zaś [math]f\;[/math] jest wzajemnie jednoznaczna, to [math]d=d'\;[/math].
CBDO
Twierdzenie
Korzystając z powyższego twierdzenia, pokażemy, że
Tw.Każda funkcja [math]f\;[/math], ciągła na odcinku [math][a,b]\;[/math], będąca bijekcją, jest ściśle monotoniczna (tzn. ściśle rosnąca bądź ściśle malejąca).
Dowód
Z założenia [math]f(a)\ne f(b)\;[/math]. Załóżmy, że [math]f(a)\lt f(b)\;[/math] (gdy jest na odwrót, rozumowanie jest analogiczne). Udowodnimy, że wtedy [math]f(x)\;[/math] jest w całym przedziale [math][a,b]\;[/math] rosnąca. Niech [math]x\lt x'\;[/math].
Trzeba pokazać, że [math]f(x)\lt f(x')\;[/math].
Zauważmy najsampierw, że warunki [math]a\leq x \leq b\;[/math] i [math]f(a)\lt f(b)\;[/math] implikują [math]f(a)\leq f(x) \leq f(b)\;[/math].
Gdyby bowiem tak nie było, to mielibyśmy albo
- [math]f(x)\lt f(a)\;[/math], albo
- [math]f(x)\gt f(b)\;[/math].
W przypadku 1. mielibyśmy nierówność: [math]f(x)\lt f(a)\lt f(b)\;[/math] i, na mocy własności Darboux, istniałby w przedziale [math][x,b]\;[/math] punkt [math]x''\;[/math] taki, że [math]f(x'')=f(a)\;[/math]; ale to przeczy założeniu, że [math]f(x)\;[/math] jest różnowartościowa (bo [math]x''\ne a\;[/math]). W przypadku 2. natomiast istniałby w przedziale [math][a,x]\;[/math] punkt [math]x'''\;[/math] taki, że [math]f(x''')=f(b)\;[/math], co z kolei jest sprzeczne z założeniem o różnowartościowości funkcji [math]f(x)\;[/math] (bo — podobnie jak uprzednio — [math]x'''\ne b\;[/math]).
Pokazaliśmy więc, że [math]f(a)\leq f(x)\leq f(b)\;[/math]. Jednocześnie wnioskujemy, że warunki [math]x\leq x'\leq b\;[/math] i [math]f(x)\lt f(b)\;[/math] pociągają za sobą [math]f(x)\leq f(x')\leq f(b)\;[/math]. Tak więc [math]f(x)\lt f(x')\;[/math].
CBDO